三角函数及平面向量知识点总结[下学期]
图片预览


文档简介
三角函数
1. 正角:逆时针旋转;负角:顺时针旋转。
2. 时针在1小时内所转的角度为-;
分针在1小时内所转的角度为-。
3. 一般地,与角终边相同的角的集合为:。
4. 终边落在直线上的角用表示。
5. (经常联系起来考察)。
6. 。
7. 对任意角:
8.
+ + - + - +
- - - + + -
9. “知其一就可以求其二”。
10.
诱导公式关键步骤:(1)把看成锐角;(2)确定符号;(3)确定函数名称。(同名函数,需换函数名称)
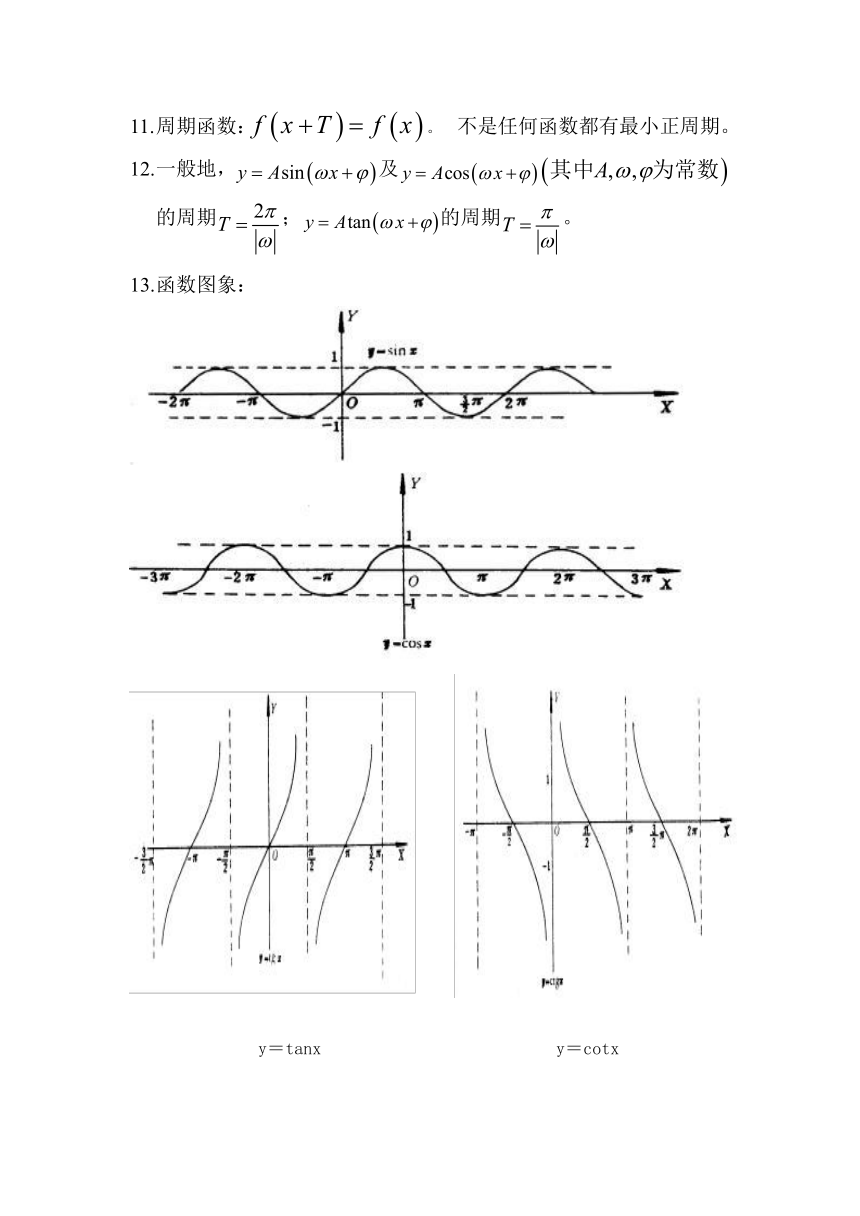
11. 周期函数:。 不是任何函数都有最小正周期。
12. 一般地,及的周期;的周期。
13. 函数图象:
y=tanx y=cotx
14. 函数性质:
函 数 y=sinx y=cosx y=tanx
定 义 域 (-∞,+∞) (-∞,+∞)
值域 [-1,1] [-1,1] (-∞,+∞)
奇偶性 奇函数 偶函数 奇函数
最小正周期 2π 2π π
单 调 性 增减 增减 递增
(注:表中k均为整数)
15. 图象平移:以变换到为例
向左平移个单位 (左加右减)
横坐标变为原来的倍(纵坐标不变)
纵坐标变为原来的4倍(横坐标不变)
横坐标变为原来的倍(纵坐标不变)
向左平移个单位 (左加右减)
纵坐标变为原来的4倍(横坐标不变)
注意:在变换中改变的始终是X。
注意:阅读章节后链接的内容,特别是反三角的表示。
平 面 向 量
1. 向量:既有大小又有方向的量。
零向量:长度为0的向量;与任何向量都平行,方向是任意的!
单位向量:长度为1的向量。
2. 平行向量(共线向量):方向相同或相反的非零向量。
3. 相等向量:大小相等方向相同。
4. B B C
O A O A
三角形法则: 平行四边形法则:
5. 向量共线定理:
6. 平面内任何向量都可以用两个不共线的向量表示,即:
7. 向量的坐标表示:
8. 一个向量的坐标表示等于该向量终点的坐标减去起点坐标(如上)
9.
10. 是在方向上的投影,它是数量。
11. 起点终点分点满足:
(起点到分点,分点到终点),则分点满足:
三角恒等变换
1. 两角和、差公式:
2. 二倍角公式:
3. 辅助角公式:
4. 注意几种角的变形:
还要注意互余、互补、特殊角间的灵活变形。
1. 正角:逆时针旋转;负角:顺时针旋转。
2. 时针在1小时内所转的角度为-;
分针在1小时内所转的角度为-。
3. 一般地,与角终边相同的角的集合为:。
4. 终边落在直线上的角用表示。
5. (经常联系起来考察)。
6. 。
7. 对任意角:
8.
+ + - + - +
- - - + + -
9. “知其一就可以求其二”。
10.
诱导公式关键步骤:(1)把看成锐角;(2)确定符号;(3)确定函数名称。(同名函数,需换函数名称)
11. 周期函数:。 不是任何函数都有最小正周期。
12. 一般地,及的周期;的周期。
13. 函数图象:
y=tanx y=cotx
14. 函数性质:
函 数 y=sinx y=cosx y=tanx
定 义 域 (-∞,+∞) (-∞,+∞)
值域 [-1,1] [-1,1] (-∞,+∞)
奇偶性 奇函数 偶函数 奇函数
最小正周期 2π 2π π
单 调 性 增减 增减 递增
(注:表中k均为整数)
15. 图象平移:以变换到为例
向左平移个单位 (左加右减)
横坐标变为原来的倍(纵坐标不变)
纵坐标变为原来的4倍(横坐标不变)
横坐标变为原来的倍(纵坐标不变)
向左平移个单位 (左加右减)
纵坐标变为原来的4倍(横坐标不变)
注意:在变换中改变的始终是X。
注意:阅读章节后链接的内容,特别是反三角的表示。
平 面 向 量
1. 向量:既有大小又有方向的量。
零向量:长度为0的向量;与任何向量都平行,方向是任意的!
单位向量:长度为1的向量。
2. 平行向量(共线向量):方向相同或相反的非零向量。
3. 相等向量:大小相等方向相同。
4. B B C
O A O A
三角形法则: 平行四边形法则:
5. 向量共线定理:
6. 平面内任何向量都可以用两个不共线的向量表示,即:
7. 向量的坐标表示:
8. 一个向量的坐标表示等于该向量终点的坐标减去起点坐标(如上)
9.
10. 是在方向上的投影,它是数量。
11. 起点终点分点满足:
(起点到分点,分点到终点),则分点满足:
三角恒等变换
1. 两角和、差公式:
2. 二倍角公式:
3. 辅助角公式:
4. 注意几种角的变形:
还要注意互余、互补、特殊角间的灵活变形。
