三角函数的应用[下学期]
图片预览




文档简介
课件13张PPT。三角函数
S= Asin(ω t + ψ )的应用
(1) 三角函数能够模拟许多周期现象,在实际问题中有广泛的应用。 如:物理中简谐振动、单摆运动、波的传播、交流电等S= Asin(ω t + ψ )
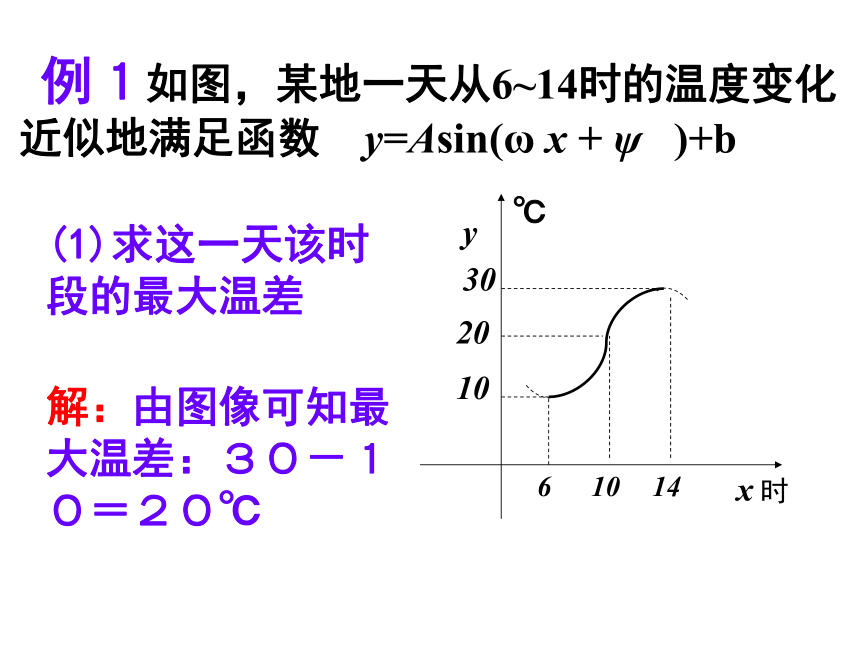
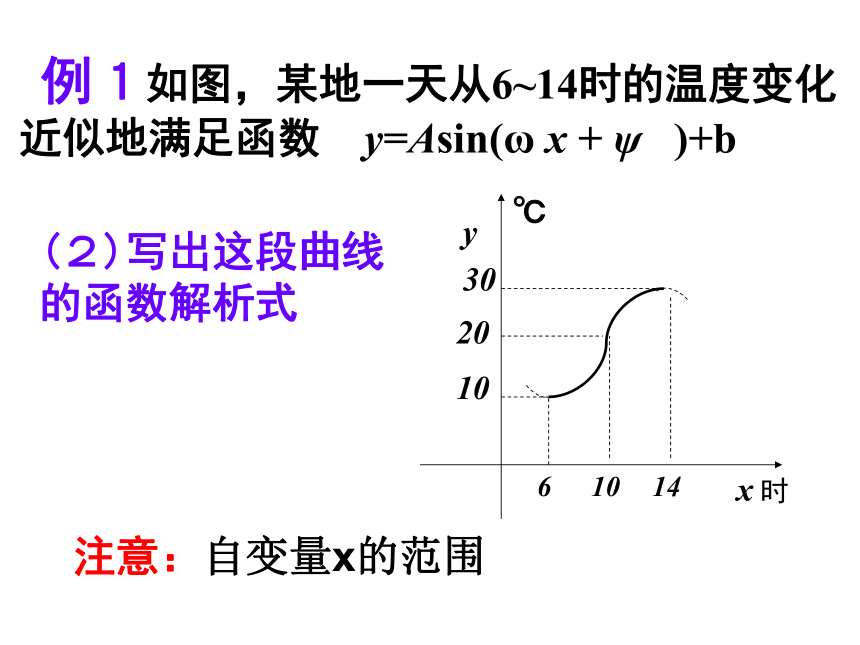
(其中 A>0, ω >0)简谐运动:位移S与时间t的函数关系为: A(振幅):表示这个量振动时离开平衡位置的最大距离;S=Asin(ω t + ψ) (A>0, ω >0) T= (周期):往复振动一周所需的时间;f = = (频率):单位时间内往复振动的次数;ψ(初相): t=0时的相位 ω t + ψ (相位) 例1如图,某地一天从6~14时的温度变化近似地满足函数 y=Asin(ω x + ψ )+b(1)求这一天该时段的最大温差解:由图像可知最大温差:30-10=20℃ 例1如图,某地一天从6~14时的温度变化近似地满足函数 y=Asin(ω x + ψ )+b(2)写出这段曲线的函数解析式注意:自变量x的范围例2、点O为做简谐运动的物体的平衡
位置,取向右的方向为物体位移的正方向。若已知振幅为3厘米,周期为3秒,且物体向右运动到距平衡位置最远时开始计时。(1)求物体对平衡位置的位x(厘米)与时间 t(秒)之间的函数关系.(2)求该物体在t=5秒时的位置.思考: 如图,点P是半径为rcm的砂轮边缘上的一个点,它从初始位置P0开始(∠XOp0= ψ ),按逆时针方向以角速度ωrad/s做圆周运动,求点P的纵坐标y关于时间t的函数关系。P0y= r sin(ωt +ψ)例3、一个半径为3m的水轮如图,水轮圆心O距离水面2m ,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现(P0)时开始计时。(1)将点P距离水面的高度Z(m)表示为时间t(s)的函数。O .例3、一个半径为3m的水轮如图,水轮圆心O距离水面2m ,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现(P0)时开始计时。(2)点P第一次到达最高点大约要多长时间?O . 三角函数应用题的解题步骤可以用下面的框图表示:数学模型的解实际应用问题数学模型练 习回顾昨天作业题 11小 结2、进一步理解和掌握三角公式和三角函数1、熟悉“建立实际问题的函数模型”基本 步骤3、进一步明白了学习三角函数的重要性
(其中 A>0, ω >0)简谐运动:位移S与时间t的函数关系为: A(振幅):表示这个量振动时离开平衡位置的最大距离;S=Asin(ω t + ψ) (A>0, ω >0) T= (周期):往复振动一周所需的时间;f = = (频率):单位时间内往复振动的次数;ψ(初相): t=0时的相位 ω t + ψ (相位) 例1如图,某地一天从6~14时的温度变化近似地满足函数 y=Asin(ω x + ψ )+b(1)求这一天该时段的最大温差解:由图像可知最大温差:30-10=20℃ 例1如图,某地一天从6~14时的温度变化近似地满足函数 y=Asin(ω x + ψ )+b(2)写出这段曲线的函数解析式注意:自变量x的范围例2、点O为做简谐运动的物体的平衡
位置,取向右的方向为物体位移的正方向。若已知振幅为3厘米,周期为3秒,且物体向右运动到距平衡位置最远时开始计时。(1)求物体对平衡位置的位x(厘米)与时间 t(秒)之间的函数关系.(2)求该物体在t=5秒时的位置.思考: 如图,点P是半径为rcm的砂轮边缘上的一个点,它从初始位置P0开始(∠XOp0= ψ ),按逆时针方向以角速度ωrad/s做圆周运动,求点P的纵坐标y关于时间t的函数关系。P0y= r sin(ωt +ψ)例3、一个半径为3m的水轮如图,水轮圆心O距离水面2m ,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现(P0)时开始计时。(1)将点P距离水面的高度Z(m)表示为时间t(s)的函数。O .例3、一个半径为3m的水轮如图,水轮圆心O距离水面2m ,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现(P0)时开始计时。(2)点P第一次到达最高点大约要多长时间?O . 三角函数应用题的解题步骤可以用下面的框图表示:数学模型的解实际应用问题数学模型练 习回顾昨天作业题 11小 结2、进一步理解和掌握三角公式和三角函数1、熟悉“建立实际问题的函数模型”基本 步骤3、进一步明白了学习三角函数的重要性
