青岛版八年级下册6.1平行四边形的性质(1)课件 (共22张PPT)
文档属性
| 名称 | 青岛版八年级下册6.1平行四边形的性质(1)课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 484.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-11 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
平行四边形的性质(1)
平行四边形概念:
两组对边分别平行的四边形叫平行四边形。
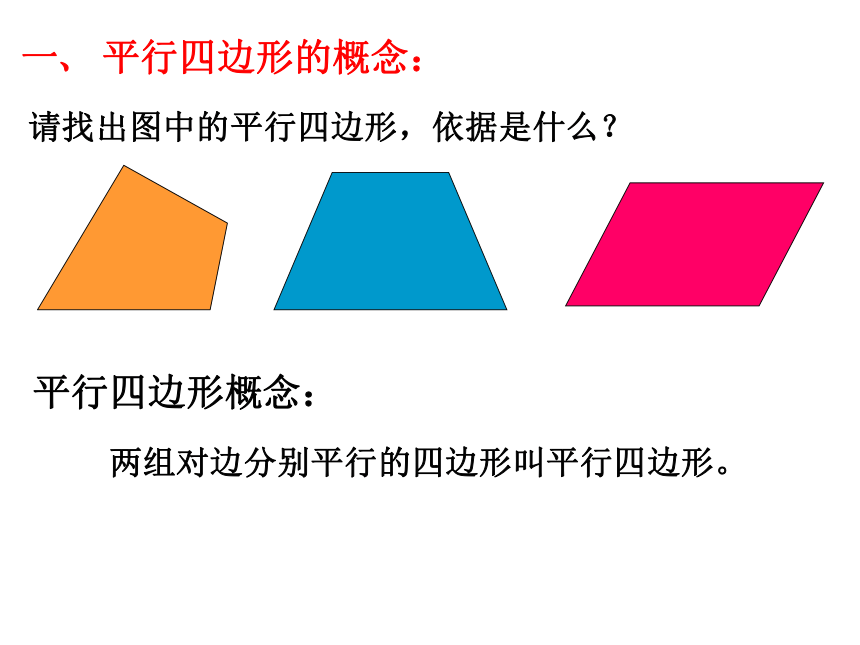
请找出图中的平行四边形,依据是什么?
一、 平行四边形的概念:
A
D
C
B
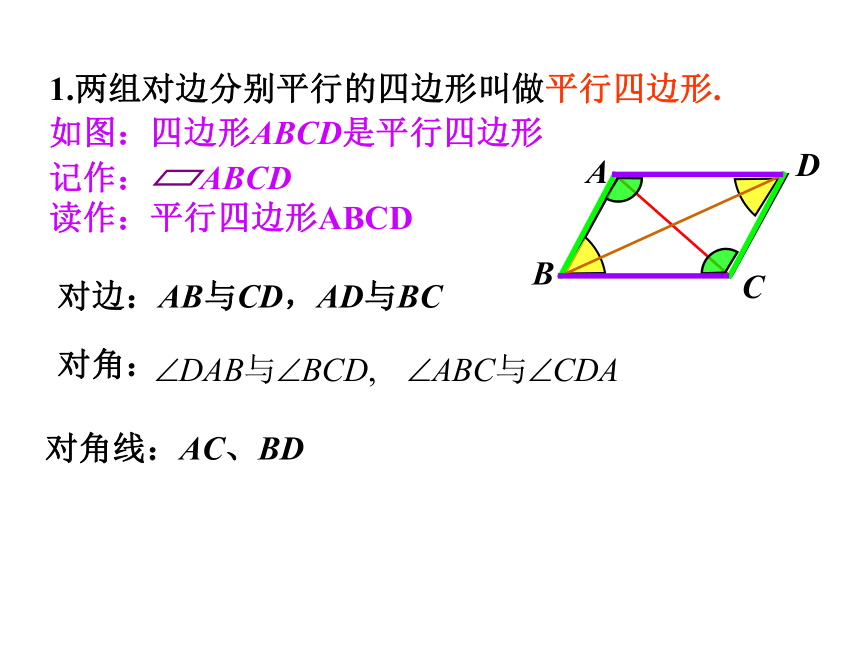
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形
记作: ABCD
读作:平行四边形ABCD
对边:AB与CD,AD与BC
对角:
对角线:AC、BD
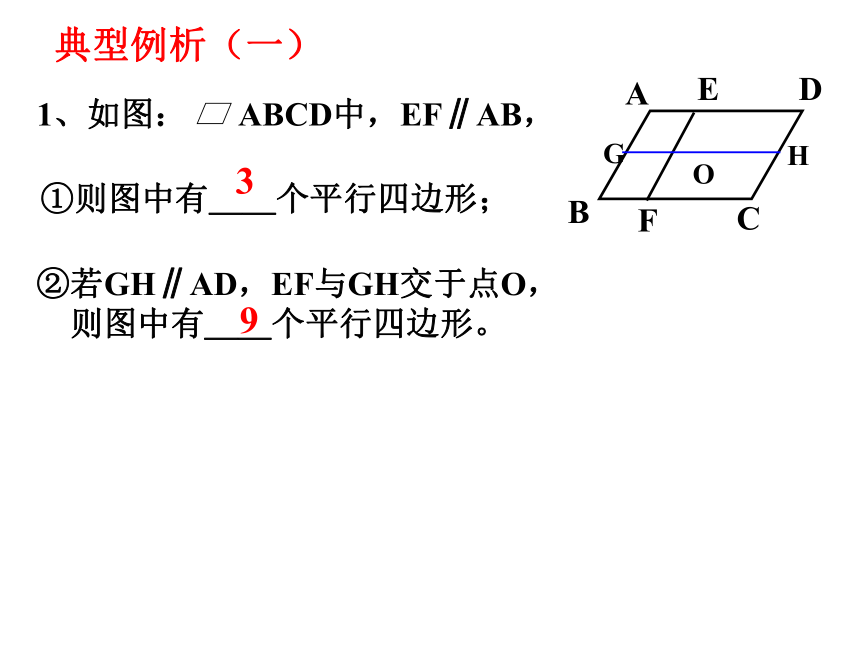
典型例析(一)
1、如图: ABCD中,EF∥AB,
A
B
C
D
F
E
①则图中有__个平行四边形;
②若GH∥AD,EF与GH交于点O,
则图中有__个平行四边形。
G
H
O
3
9
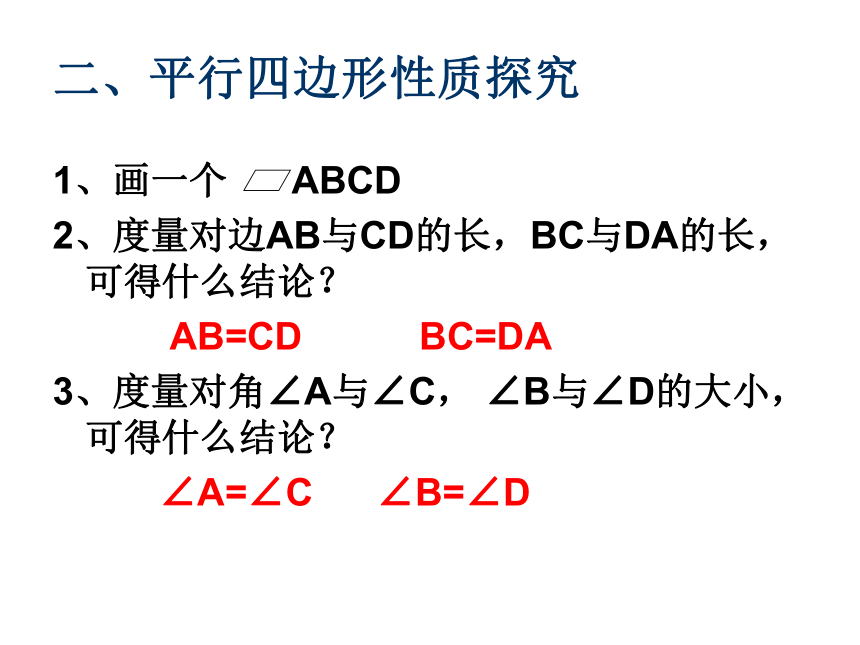
二、平行四边形性质探究
1、画一个 ABCD
2、度量对边AB与CD的长,BC与DA的长,可得什么结论?
AB=CD BC=DA
3、度量对角∠A与∠C, ∠B与∠D的大小,可得什么结论?
∠A=∠C ∠B=∠D
4、上列结论一定成立吗?怎样证明?
已知:如图,四边形ABCD
是平行四边形
求证:AB=CD,BC=DA,
∠A=∠C,∠B=∠D.
A
B
C
D
证明:
连结AC
在 ABCD中,有AD∥BC、AB∥CD
∴∠1=∠2,∠3=∠4
1
2
3
4
∵AC=AC
∴ ABC≌ CDA
∴AD=BC,AB=CD,∠B=∠D
又∵∠1=∠2,∠3 =∠4
∴ ∠1+∠3= ∠2 +∠4
即∠BAD=∠BCD
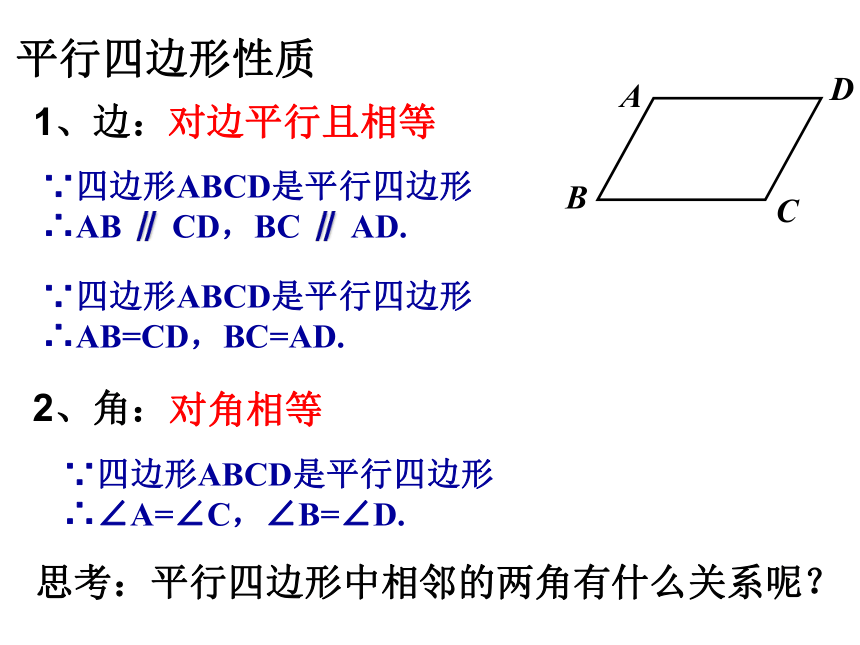
平行四边形性质
1、边:
2、角:
对角相等
对边平行且相等
∵四边形ABCD是平行四边形∴AB ∥ CD,BC ∥ AD.
∵四边形ABCD是平行四边形∴AB=CD,BC=AD.
A
D
C
B
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
思考:平行四边形中相邻的两角有什么关系呢?
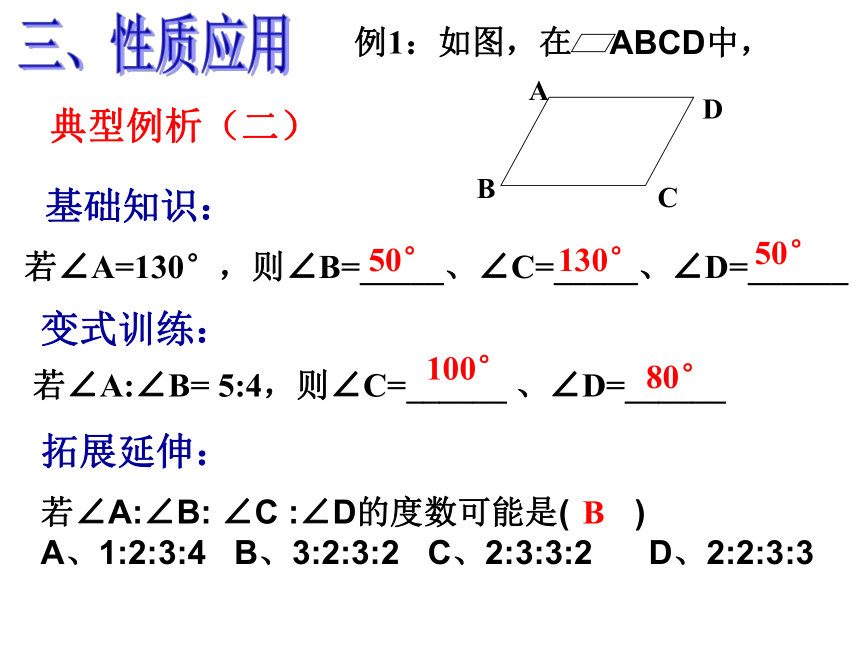
典型例析(二)
三、性质应用
若∠A=130°,则∠B=_____、∠C=_____、∠D=______
例1:如图,在
ABCD中,
变式训练:
若∠A:∠B= 5:4,则∠C=______ 、∠D=______
C
D
A
B
50°
130°
50°
100°
80°
基础知识:
若∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2 C、2:3:3:2 D、2:2:3:3
B
拓展延伸:
典型例析(三)
例:如图在
ABCD中
A基础知识:
B变式训练:
若AB:BC=3:4,周长为14㎝,则CD=__,DA=__
C拓展延伸:
C
D
A
B
3cm
4cm
若ABCD中, AB-CB=4cm,周长为32cm,则AB=____ 。
ABCD的周长为40cm,⊿ABC的周长为25cm,
则对角 线AC长为______。
10cm
5cm
综合练习:
AB=5,BC=9,BE平分
∠ABC,则AE= _____
DF=______
5
ABCD中,
1、如图,
A
D
C
B
E
1
2
F
4
2.如图, ABCD中,AB=5,BC=9,BE,CF分别平分∠ABC, ∠BCD,则DE=_____,AF=_____,EF=_____
E
F
A
D
C
B
3.如图 ABC,AB=AC=10,DE∥AC,EF∥AB则四边形ADEF的周长为_____
4
4
1
20
B
A
C
D
F
E
4.如图,在平面直角坐标系中, OBCD的顶点
O﹑B﹑D的坐标如图所示,则顶点C的坐标为
( )
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3)
C. (7,3) D. (8,2)
C
求证:(1)夹在两条平行线间的平行线段相等
A
B
C
D
a
b
典型例析(四)
(2)如果两条直线平行,那么一条直线上各点到另一条直线的距离相等
A
B
C
D
a
b
两条平行线中,一条直线上的点到另一条直线的距离叫做这两条平行线之间的距离。
性质:两条平行线之间的距离处处相等
1、如图,已知AD//BC,判断 与
是否相等,并说明理由。
四、拓展延伸: (面积问题)
E
F
A
B
C
D
M
过M作MP⊥AB
P
由
故
S =MP·BC
ABCD
ABCD
2.若M为平行四边形ABCD中AD边上一点, CMB的面积与 ABCD的面积有什么关系
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
有两组对边分别平行的四边形,叫做平行四边形。
课堂小结
角:对角相等,邻角互补
边:对边平行且相等
3.性质的应用
本节课主要学习了哪些知识
2.平行四边形的性质
1.平行四边形定义:
1.如图, ABCD中, ABE的面积S, ADE, BCE
面积分别是S1,S2,则S与S1+S2的大小关系是____
课外思考
B
E
D
C
A
S1
S
S2
2.等边 ABC的边长为10,P为 ABC内一点,PD∥ AB,PE ∥AC,PF ∥BC, 则PD+PE+PF的值为______
D
F
P
C
E
B
A
3.如图,已知点C在BD上,△ABC中
且四边形ACDE是平行四边形,那么,图中与ED相
等的线段有_______;与 相等的角有 。
A
B
C
D
E
选做题
1、平行四边形一个角的平分线分对边为5和4两部分,求这个平行四边形的周长。
2、如图,在 ABCD中,点E,F在对角线AC上,且AE=CF.请你以点F为一个端点,和图中已标明字母的某一点连成一条线段,猜想并证明它和图中已有的某一线段相等(只需证明一组线段相等即可).
(1)连结_________
(2)猜想:________=_________.
(3)证明:
平行四边形的性质(1)
平行四边形概念:
两组对边分别平行的四边形叫平行四边形。
请找出图中的平行四边形,依据是什么?
一、 平行四边形的概念:
A
D
C
B
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形
记作: ABCD
读作:平行四边形ABCD
对边:AB与CD,AD与BC
对角:
对角线:AC、BD
典型例析(一)
1、如图: ABCD中,EF∥AB,
A
B
C
D
F
E
①则图中有__个平行四边形;
②若GH∥AD,EF与GH交于点O,
则图中有__个平行四边形。
G
H
O
3
9
二、平行四边形性质探究
1、画一个 ABCD
2、度量对边AB与CD的长,BC与DA的长,可得什么结论?
AB=CD BC=DA
3、度量对角∠A与∠C, ∠B与∠D的大小,可得什么结论?
∠A=∠C ∠B=∠D
4、上列结论一定成立吗?怎样证明?
已知:如图,四边形ABCD
是平行四边形
求证:AB=CD,BC=DA,
∠A=∠C,∠B=∠D.
A
B
C
D
证明:
连结AC
在 ABCD中,有AD∥BC、AB∥CD
∴∠1=∠2,∠3=∠4
1
2
3
4
∵AC=AC
∴ ABC≌ CDA
∴AD=BC,AB=CD,∠B=∠D
又∵∠1=∠2,∠3 =∠4
∴ ∠1+∠3= ∠2 +∠4
即∠BAD=∠BCD
平行四边形性质
1、边:
2、角:
对角相等
对边平行且相等
∵四边形ABCD是平行四边形∴AB ∥ CD,BC ∥ AD.
∵四边形ABCD是平行四边形∴AB=CD,BC=AD.
A
D
C
B
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
思考:平行四边形中相邻的两角有什么关系呢?
典型例析(二)
三、性质应用
若∠A=130°,则∠B=_____、∠C=_____、∠D=______
例1:如图,在
ABCD中,
变式训练:
若∠A:∠B= 5:4,则∠C=______ 、∠D=______
C
D
A
B
50°
130°
50°
100°
80°
基础知识:
若∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2 C、2:3:3:2 D、2:2:3:3
B
拓展延伸:
典型例析(三)
例:如图在
ABCD中
A基础知识:
B变式训练:
若AB:BC=3:4,周长为14㎝,则CD=__,DA=__
C拓展延伸:
C
D
A
B
3cm
4cm
若ABCD中, AB-CB=4cm,周长为32cm,则AB=____ 。
ABCD的周长为40cm,⊿ABC的周长为25cm,
则对角 线AC长为______。
10cm
5cm
综合练习:
AB=5,BC=9,BE平分
∠ABC,则AE= _____
DF=______
5
ABCD中,
1、如图,
A
D
C
B
E
1
2
F
4
2.如图, ABCD中,AB=5,BC=9,BE,CF分别平分∠ABC, ∠BCD,则DE=_____,AF=_____,EF=_____
E
F
A
D
C
B
3.如图 ABC,AB=AC=10,DE∥AC,EF∥AB则四边形ADEF的周长为_____
4
4
1
20
B
A
C
D
F
E
4.如图,在平面直角坐标系中, OBCD的顶点
O﹑B﹑D的坐标如图所示,则顶点C的坐标为
( )
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3)
C. (7,3) D. (8,2)
C
求证:(1)夹在两条平行线间的平行线段相等
A
B
C
D
a
b
典型例析(四)
(2)如果两条直线平行,那么一条直线上各点到另一条直线的距离相等
A
B
C
D
a
b
两条平行线中,一条直线上的点到另一条直线的距离叫做这两条平行线之间的距离。
性质:两条平行线之间的距离处处相等
1、如图,已知AD//BC,判断 与
是否相等,并说明理由。
四、拓展延伸: (面积问题)
E
F
A
B
C
D
M
过M作MP⊥AB
P
由
故
S =MP·BC
ABCD
ABCD
2.若M为平行四边形ABCD中AD边上一点, CMB的面积与 ABCD的面积有什么关系
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
有两组对边分别平行的四边形,叫做平行四边形。
课堂小结
角:对角相等,邻角互补
边:对边平行且相等
3.性质的应用
本节课主要学习了哪些知识
2.平行四边形的性质
1.平行四边形定义:
1.如图, ABCD中, ABE的面积S, ADE, BCE
面积分别是S1,S2,则S与S1+S2的大小关系是____
课外思考
B
E
D
C
A
S1
S
S2
2.等边 ABC的边长为10,P为 ABC内一点,PD∥ AB,PE ∥AC,PF ∥BC, 则PD+PE+PF的值为______
D
F
P
C
E
B
A
3.如图,已知点C在BD上,△ABC中
且四边形ACDE是平行四边形,那么,图中与ED相
等的线段有_______;与 相等的角有 。
A
B
C
D
E
选做题
1、平行四边形一个角的平分线分对边为5和4两部分,求这个平行四边形的周长。
2、如图,在 ABCD中,点E,F在对角线AC上,且AE=CF.请你以点F为一个端点,和图中已标明字母的某一点连成一条线段,猜想并证明它和图中已有的某一线段相等(只需证明一组线段相等即可).
(1)连结_________
(2)猜想:________=_________.
(3)证明:
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
