2022—2023学年青岛版数学八年级下册 6.2平行四边形的判定(1)课件 (共25张PPT)
文档属性
| 名称 | 2022—2023学年青岛版数学八年级下册 6.2平行四边形的判定(1)课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 868.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-11 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
青岛版数学教材八年级下
6.2平行四边形的判定(1)
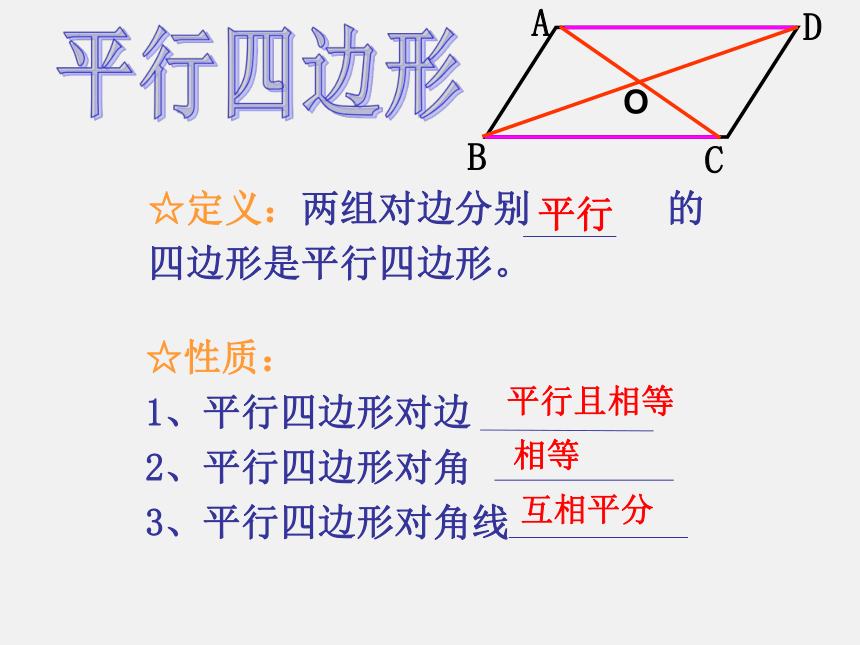
平行四边形
☆定义:两组对边分别 的四边形是平行四边形。
☆性质:
1、平行四边形对边
2、平行四边形对角
3、平行四边形对角线
相等
互相平分
平行且相等
平行
A
B
C
D
O
一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)
生活实际的挑战
A
B
C
想一想
方法(一)
D
A
B
C
(两组对边分别平行的四边形是平行四边形)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
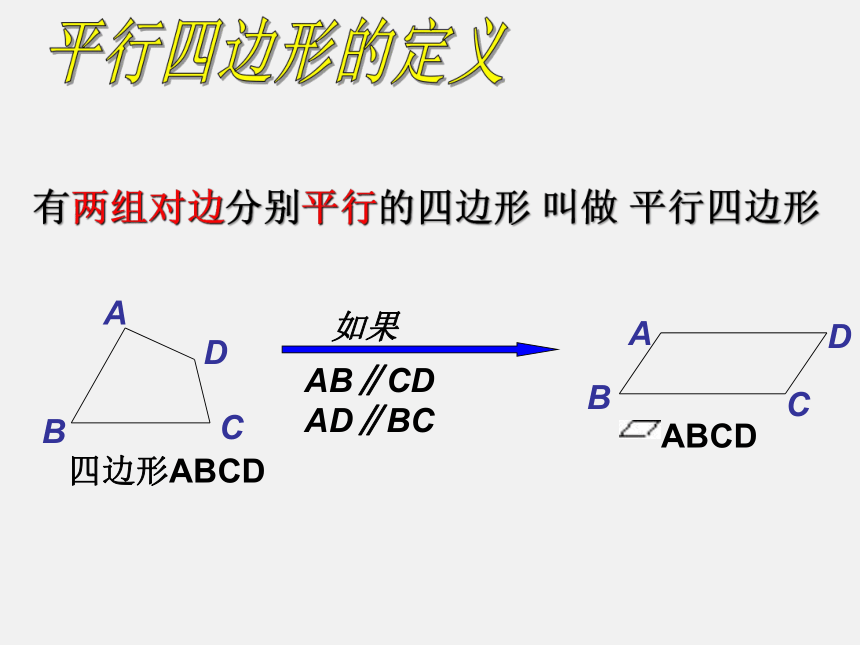
有两组对边分别平行的四边形
叫做
平行四边形
平行四边形的定义
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
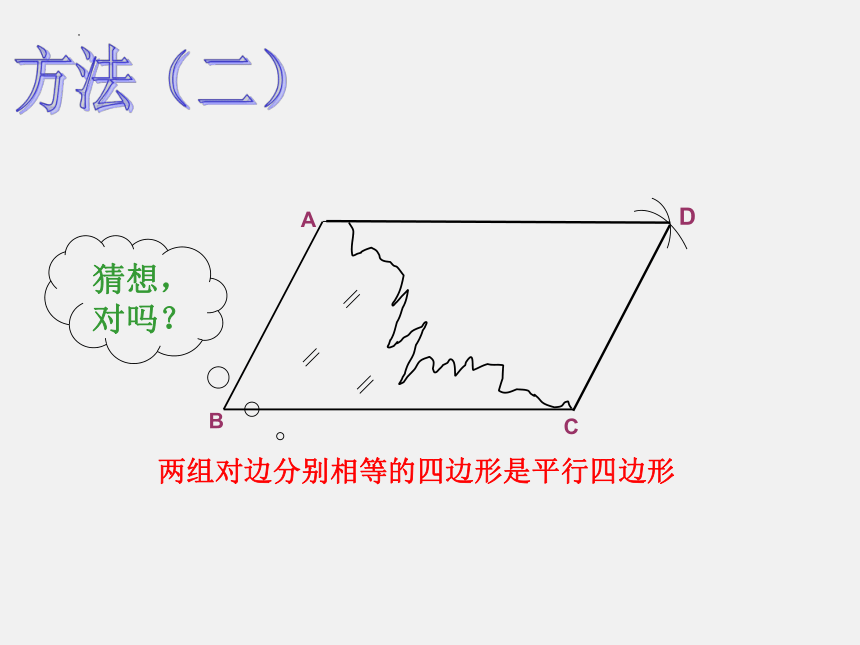
方法(二)
D
A
B
C
两组对边分别相等的四边形是平行四边形
猜想,对吗?
A
B
C
D
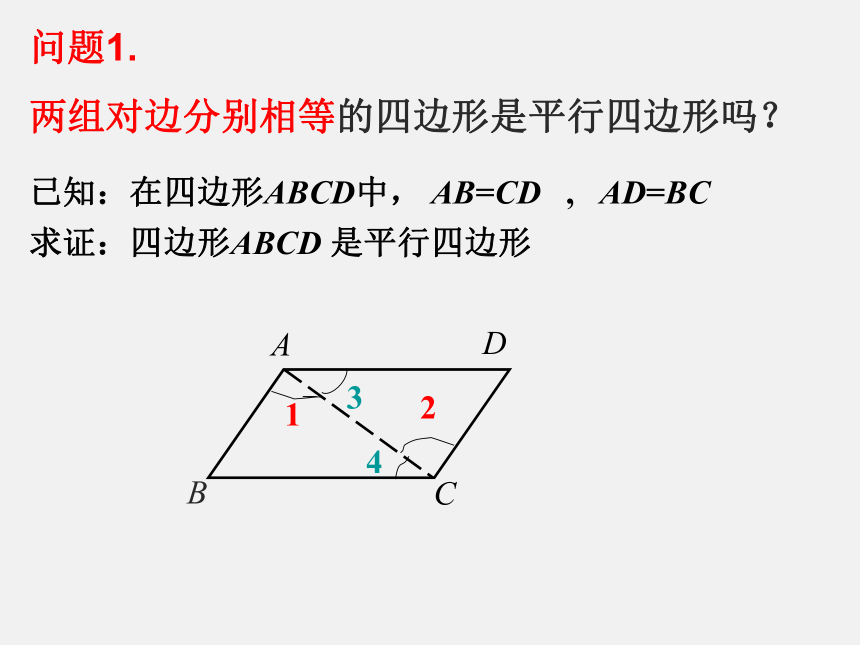
已知:在四边形ABCD中, AB=CD , AD=BC
求证:四边形ABCD 是平行四边形
1
2
3
4
问题1.
两组对边分别相等的四边形是平行四边形吗?
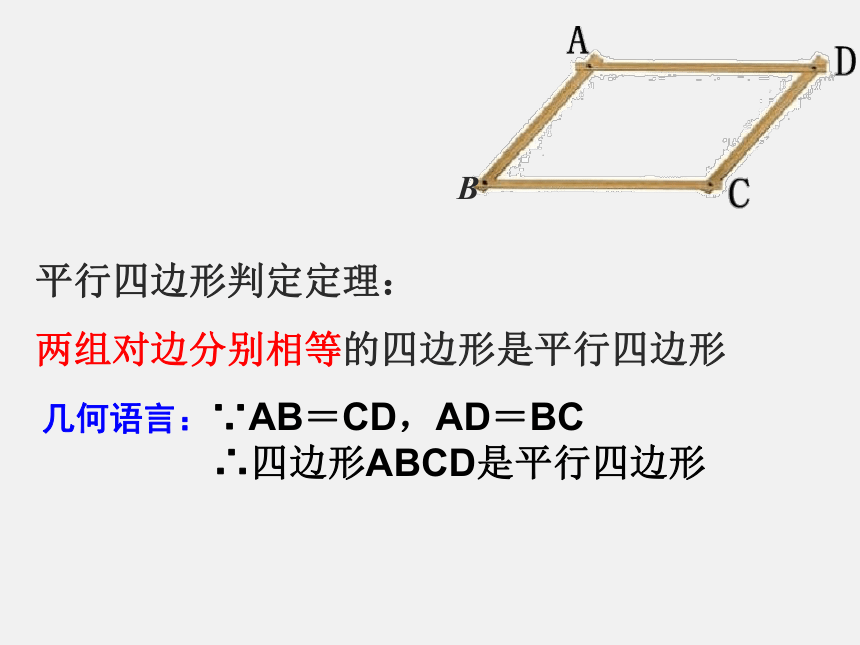
平行四边形判定定理:
两组对边分别相等的四边形是平行四边形
B
几何语言:∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
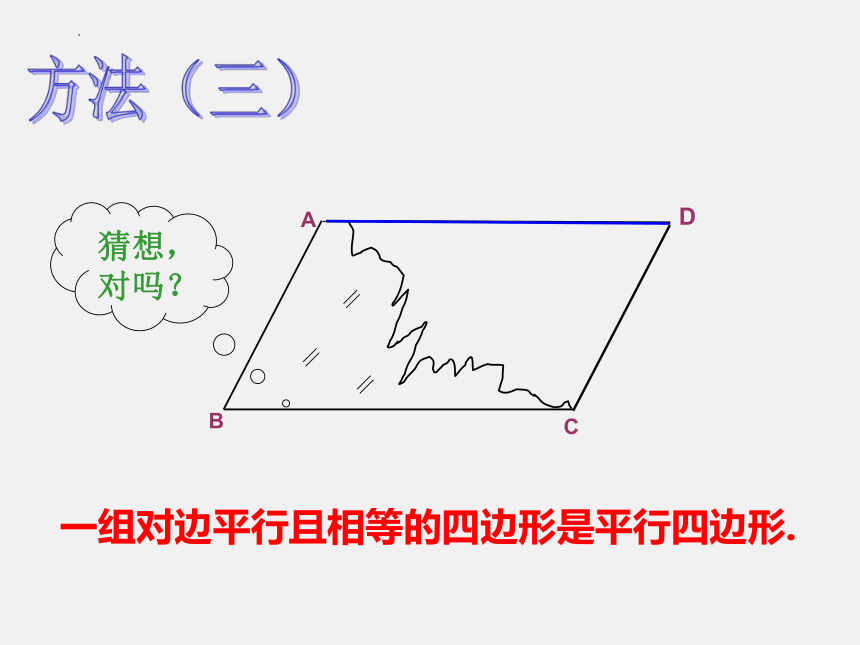
方法(三)
D
A
B
C
一组对边平行且相等的四边形是平行四边形.
猜想,对吗?
问题2.
一组对边平行且相等的四边形是平行四边形吗?
A
B
C
D
已知:在四边形ABCD中, AB∥CD , AB=CD
求证:四边形ABCD 是平行四边形
1
2
3
4
平行四边形判定定理:
一组对边平行且相等的四边形是平行四边形
B
几何语言:∵AB=CD,AB ∥ CD
∴四边形ABCD是平行四边形
请你识别下列四边形哪些是平行四边形 请说明理由?
说一说
A
D
C
B
110°
70°
110°
⑴
⑶
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
A
B
C
D
120°
60°
5㎝
5㎝
⑵
练一练
判断正误
1.一组对边相等的四边形是平行四边形
2.一组对边平行且另一组对边相等的四边形是平行四边形
3. 一组对边平行且相等的四边形是平行四边形
×
×
√
练一练
1.□ABCD中,点E、F分别是BC、AD的中点,四边形ABFE和CDEF是平行四边形吗?说说你的理由。
A
B
C
D
E
F
2.□ABCD中,点E、F分别是BC、AD的中点,
求证:四边形BEDF是平行四边形。
A
B
C
D
E
F
练一练
3.□四边形ABCD中,点E、F分别是BC、AD的中点,
图中有几个平行四边形?说明理由。
A
B
C
D
E
F
G
H
例2:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
D
A
B
C
E
F
大显身手
求证:四边形BFDE是平行四边形
已知:E、F是平行四边形ABCD对角线AC上的两点,并且BE ∥ DF.
求证:四边形BFDE是平行四边形
D
A
B
C
E
F
变式练习1:
变式练习2:
已知:E、F是平行四边形ABCD对角线AC延长线上的两点,并且AE=CF.
D
A
B
C
E
F
求证:四边形BFDE是平行四边形
课堂小结:
1、今天学行四边形的哪些判定方法?
2、这些判定方法的几何语言是什么?
两组对边分别相等
两组对边分别平行
平行四边形的判定方法
一组对边平行且相等
的四边形是平行四边形
边
A
B
C
D
判定 文字语言 图形语 符号语言
定义 两组对边分别平行的四边形是平行四边形 ∵AB∥CD,
AD∥BC
∴…是平行四边形
定理1 一组对边平行且相等的四边形是平等四边形 ∵AB=CD,
AB∥CD
∴…是平行四边形
定理2 两组对边分别相等的四边形是平行四边形 ∵AB=CD,
AD=BC
∴…是平行四边形
3 未完待续。。。。。。
推论 未完待续。。。。。。
A
B
C
D
A
B
C
D
A
B
C
D
达标检测
1、已知四边形ABCD,在(1)AB//CD;(2)AB=CD;(3)BC//AD;(4)BC=AD四个条件中任意选两个,不能使四边形ABCD是平行四边形的有( )
A.(1)(2) B.(2)(3) C.(1)(3) D.(3)(4)
2.已知,如图,四边形AEFD、EBCF都是平行四边形,求证:四边形ABCD是平行四边形。
1.已知:E、F是 ABCD对角线AC上的两点,BE∥DF。求证:四边形BFDE是平行四边形
D
A
B
C
E
F
2.如图,点E、F、G、H是 ABCD的边AD、AB、BC、CD上的点,AE=CG,BF=DH。求证:四边形EFGH是平行四边形
青岛版数学教材八年级下
6.2平行四边形的判定(1)
平行四边形
☆定义:两组对边分别 的四边形是平行四边形。
☆性质:
1、平行四边形对边
2、平行四边形对角
3、平行四边形对角线
相等
互相平分
平行且相等
平行
A
B
C
D
O
一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)
生活实际的挑战
A
B
C
想一想
方法(一)
D
A
B
C
(两组对边分别平行的四边形是平行四边形)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
有两组对边分别平行的四边形
叫做
平行四边形
平行四边形的定义
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
方法(二)
D
A
B
C
两组对边分别相等的四边形是平行四边形
猜想,对吗?
A
B
C
D
已知:在四边形ABCD中, AB=CD , AD=BC
求证:四边形ABCD 是平行四边形
1
2
3
4
问题1.
两组对边分别相等的四边形是平行四边形吗?
平行四边形判定定理:
两组对边分别相等的四边形是平行四边形
B
几何语言:∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
方法(三)
D
A
B
C
一组对边平行且相等的四边形是平行四边形.
猜想,对吗?
问题2.
一组对边平行且相等的四边形是平行四边形吗?
A
B
C
D
已知:在四边形ABCD中, AB∥CD , AB=CD
求证:四边形ABCD 是平行四边形
1
2
3
4
平行四边形判定定理:
一组对边平行且相等的四边形是平行四边形
B
几何语言:∵AB=CD,AB ∥ CD
∴四边形ABCD是平行四边形
请你识别下列四边形哪些是平行四边形 请说明理由?
说一说
A
D
C
B
110°
70°
110°
⑴
⑶
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
A
B
C
D
120°
60°
5㎝
5㎝
⑵
练一练
判断正误
1.一组对边相等的四边形是平行四边形
2.一组对边平行且另一组对边相等的四边形是平行四边形
3. 一组对边平行且相等的四边形是平行四边形
×
×
√
练一练
1.□ABCD中,点E、F分别是BC、AD的中点,四边形ABFE和CDEF是平行四边形吗?说说你的理由。
A
B
C
D
E
F
2.□ABCD中,点E、F分别是BC、AD的中点,
求证:四边形BEDF是平行四边形。
A
B
C
D
E
F
练一练
3.□四边形ABCD中,点E、F分别是BC、AD的中点,
图中有几个平行四边形?说明理由。
A
B
C
D
E
F
G
H
例2:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
D
A
B
C
E
F
大显身手
求证:四边形BFDE是平行四边形
已知:E、F是平行四边形ABCD对角线AC上的两点,并且BE ∥ DF.
求证:四边形BFDE是平行四边形
D
A
B
C
E
F
变式练习1:
变式练习2:
已知:E、F是平行四边形ABCD对角线AC延长线上的两点,并且AE=CF.
D
A
B
C
E
F
求证:四边形BFDE是平行四边形
课堂小结:
1、今天学行四边形的哪些判定方法?
2、这些判定方法的几何语言是什么?
两组对边分别相等
两组对边分别平行
平行四边形的判定方法
一组对边平行且相等
的四边形是平行四边形
边
A
B
C
D
判定 文字语言 图形语 符号语言
定义 两组对边分别平行的四边形是平行四边形 ∵AB∥CD,
AD∥BC
∴…是平行四边形
定理1 一组对边平行且相等的四边形是平等四边形 ∵AB=CD,
AB∥CD
∴…是平行四边形
定理2 两组对边分别相等的四边形是平行四边形 ∵AB=CD,
AD=BC
∴…是平行四边形
3 未完待续。。。。。。
推论 未完待续。。。。。。
A
B
C
D
A
B
C
D
A
B
C
D
达标检测
1、已知四边形ABCD,在(1)AB//CD;(2)AB=CD;(3)BC//AD;(4)BC=AD四个条件中任意选两个,不能使四边形ABCD是平行四边形的有( )
A.(1)(2) B.(2)(3) C.(1)(3) D.(3)(4)
2.已知,如图,四边形AEFD、EBCF都是平行四边形,求证:四边形ABCD是平行四边形。
1.已知:E、F是 ABCD对角线AC上的两点,BE∥DF。求证:四边形BFDE是平行四边形
D
A
B
C
E
F
2.如图,点E、F、G、H是 ABCD的边AD、AB、BC、CD上的点,AE=CG,BF=DH。求证:四边形EFGH是平行四边形
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
