2022—2023学年青岛版数学八年级下册6.3 特殊的平行四边形 正方形的性质 课件(共34张PPT)
文档属性
| 名称 | 2022—2023学年青岛版数学八年级下册6.3 特殊的平行四边形 正方形的性质 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-11 13:09:40 | ||
图片预览



文档简介
(共34张PPT)
正方形的性质
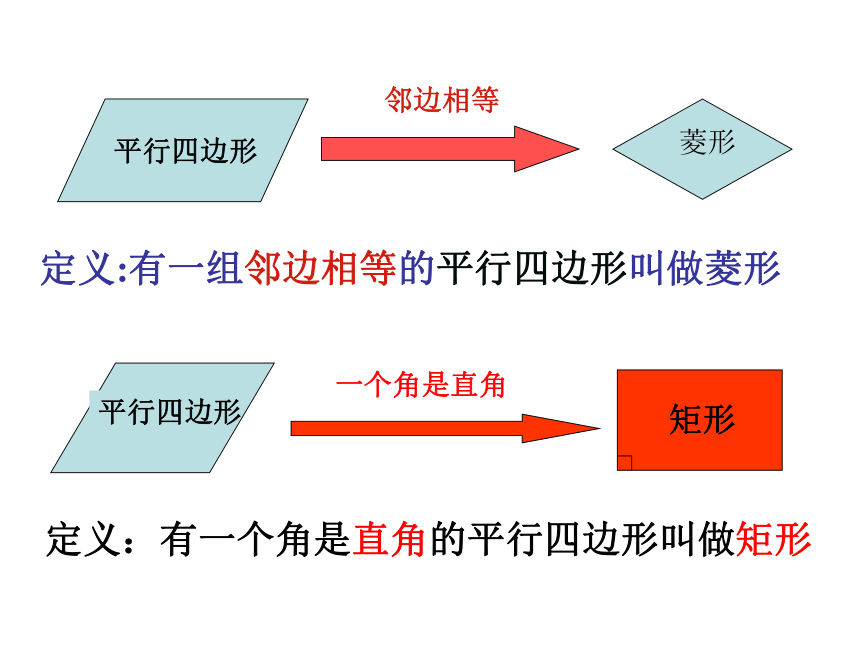
平行四边形
菱形
定义:有一组邻边相等的平行四边形叫做菱形
平行四边形
一个角是直角
矩形
定义:有一个角是直角的平行四边形叫做矩形
邻边相等
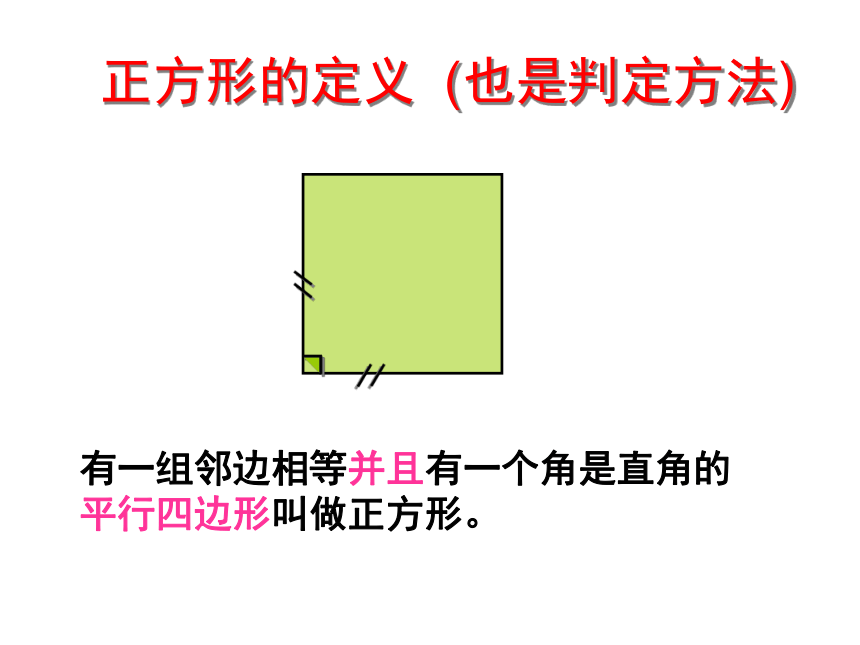
正方形的定义 (也是判定方法)
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
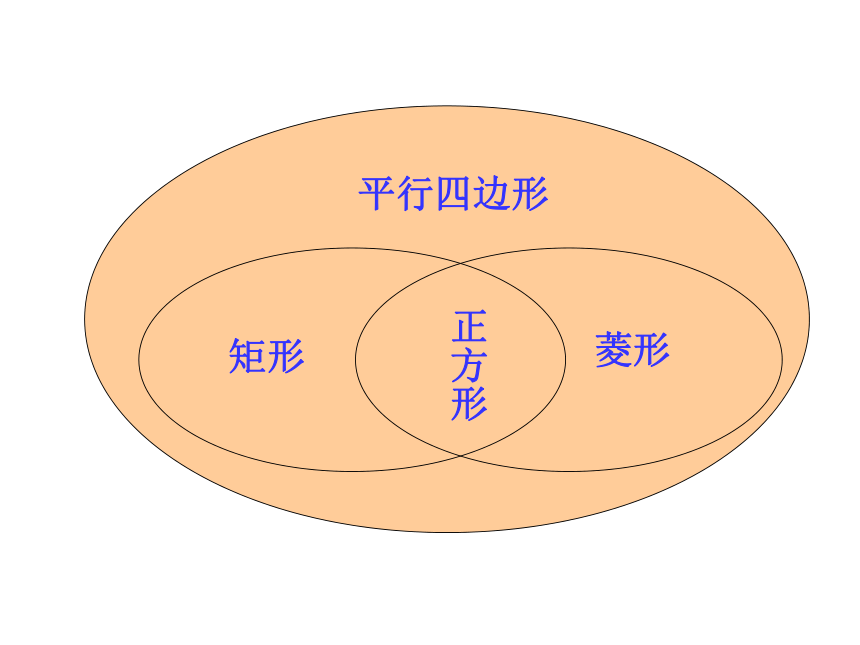
平行四边形
矩形
菱形
正方形
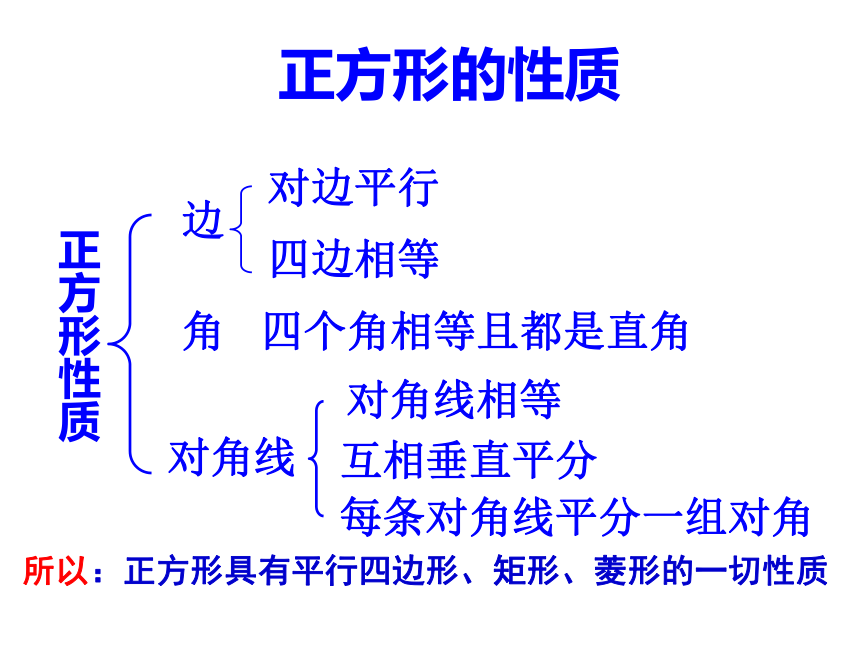
正方形的性质
边
对角线
对边平行
四边相等
对角线相等
互相垂直平分
每条对角线平分一组对角
四个角相等且都是直角
角
正方形性质
所以:正方形具有平行四边形、矩形、菱形的一切性质
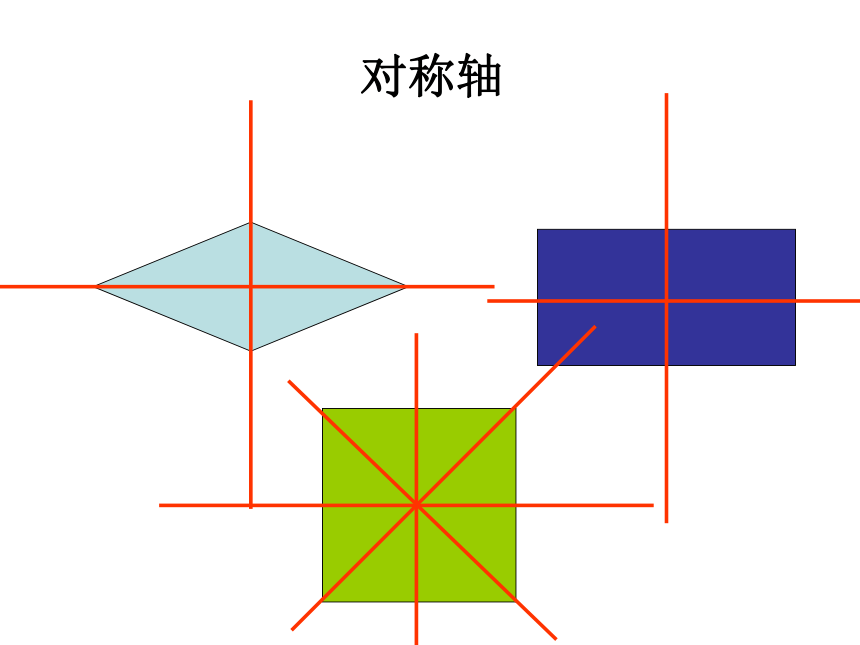
对称轴
1、判断。
(1)正方形一定是矩形。( )
(2)正方形一定是菱形。( )
(3)菱形一定是正方形。( )
(4)矩形一定是正方形。( )
(5)正方形、矩形、菱形都是平行四边形。( )
√
√
×
×
√
2、在下列性质中,平行四边形具有的是_______,矩形具有的是_________,菱形具有的是___ __ _,正方形具有的是_______________。
(1)四边都相等; (2)对角线互相平分;
(3)对角线相等; (4)对角线互相垂直;
(5)四个角都是直角;
(6)每条对角线平分一组对角;
(7)对边相等且平行;
(8)有两条对称轴。
②⑦
②③⑤⑦⑧
①②④⑥⑦⑧
①②③④⑤⑥⑦
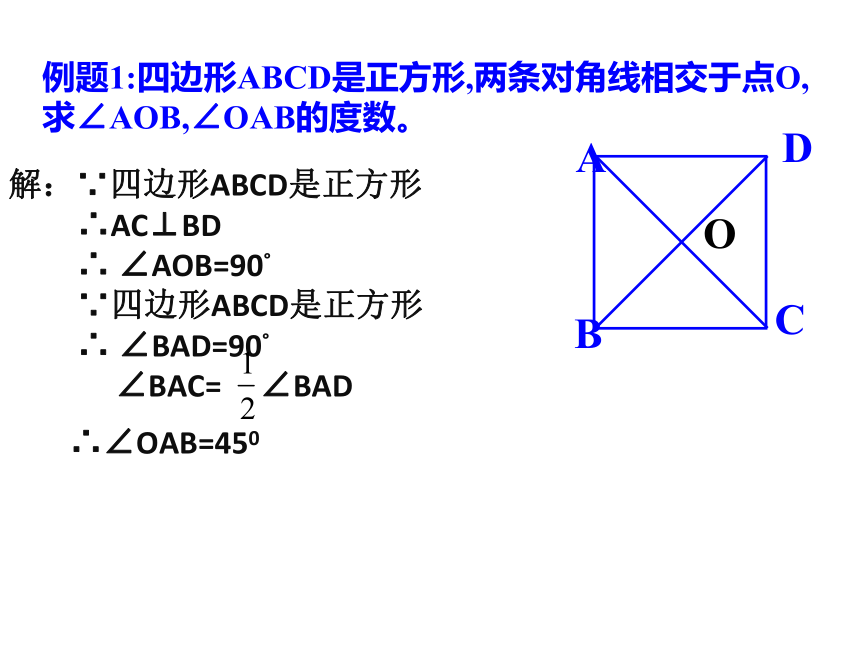
例题1:四边形ABCD是正方形,两条对角线相交于点O,
求∠AOB,∠OAB的度数。
解:∵四边形ABCD是正方形
∴AC⊥BD
∴ ∠AOB=90°
∵四边形ABCD是正方形
∴ ∠BAD=90°
∠BAC= ∠BAD
∴∠OAB=450
A
B
C
D
O
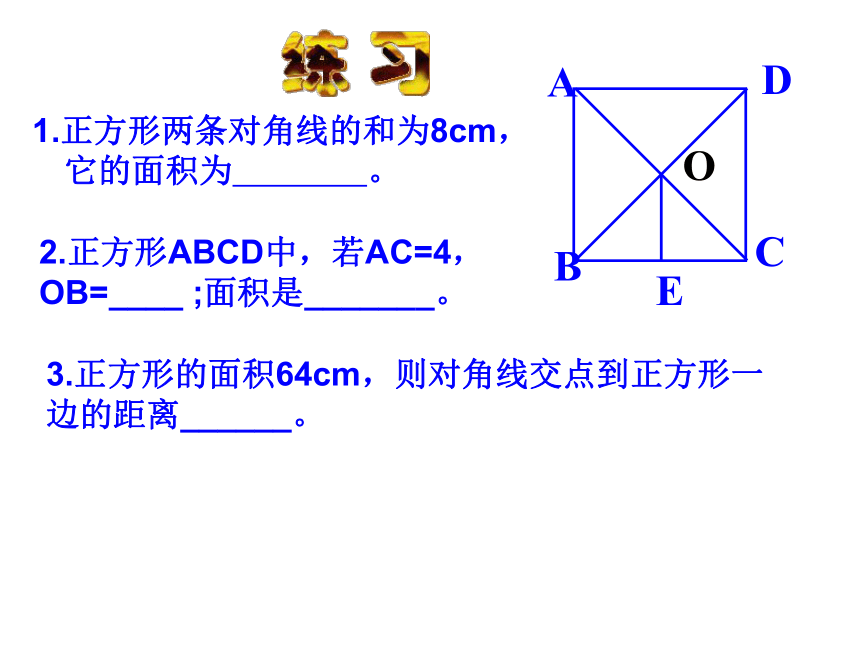
1.正方形两条对角线的和为8cm,它的面积为 。
A
B
C
D
O
E
2.正方形ABCD中,若AC=4,OB=____ ;面积是_______。
3.正方形的面积64cm,则对角线交点到正方形一边的距离______。
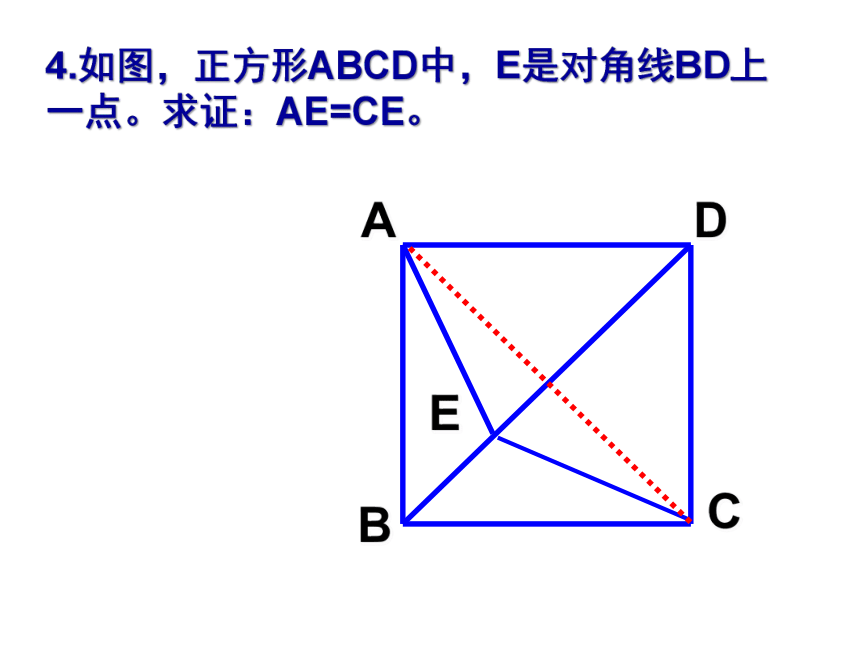
4.如图,正方形ABCD中,E是对角线BD上一点。求证:AE=CE。
A
C
B
D
E
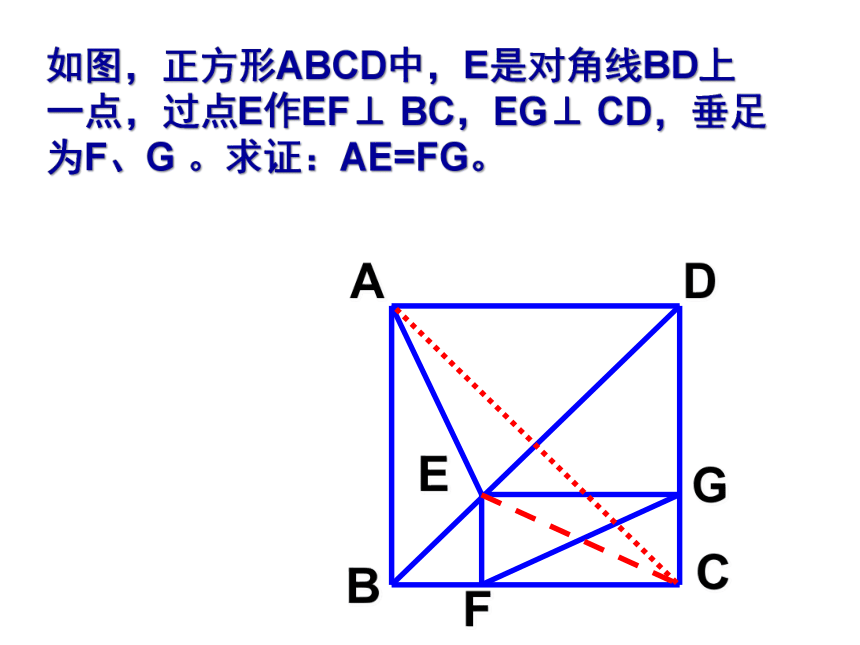
如图,正方形ABCD中,E是对角线BD上一点,过点E作EF⊥ BC,EG⊥ CD,垂足为F、G 。求证:AE=FG。
A
C
B
D
F
G
E
例2、如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由。
若将条件“BE=CF”改为”AE⊥BF“,
能否证明”AE=BF”
E
变式一:
如图,在正方形ABCD中,E、P、F三点分别在AB、BC、CD上,且AP⊥EF,AP=5cm,则EF=_____。
A
B
C
D
p
F
G
变式二:
如图,在正方形ABCD中,MN=13,且GH
垂直NM,则GH=_____。
A
B
C
D
G
H
E
M
N
F
例3:AC为正方形ABCD的对角线,E为AC上一点,且AB=AE, EF⊥AC交BC于F. (1)求证:EC=EF=FB
(2)若AC=13,
求△EFC的周长
A
B
C
D
E
F
┌
在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
变式练习 :
G
A
D
C
B
E
F
例4.已知:如图,在正方形ABCD中,E是BC的中点,点F在 CD上,∠FAE=∠BAE,求证:AF=BC+FC
例4.已知:如图,在正方形ABCD中,E是BC的中点,点F在 CD上,∠FAE=∠BAE,求证:AF=BC+FC
G
A
D
C
B
E
F
变式练习:
已知:如图,在正方形ABCD中,E是BC的中点,点F在CD 上,且AE⊥EF
求证:AF=BC+FC
A
D
C
B
E
F
G
∟
G
变式练习:
已知:如图,在正方形ABCD中,E是BC的中点,点F在CD 上,且AE⊥EF
求证:AF=BC+FC
A
D
C
B
E
F
∟
O
A
D
C
B
例5、已知:如图,正方形ABCD的对角线AC、BD相交于点O;正方形A’B’C’D’的顶点A’与点O重合,A’ B’交BC于点E,A’D’交CD于点F,求证:OE=OF
A’
B’
D’
C’
E
F
1
2
3
4
5
(1)观察四边形OECF的面积与正方形ABCD的面积有何关系?
(2)如果将正方形A’B’C’D’换成扇形OB’D’,满足什么条件时上述的关系还成立吗?
A’
B’
D’
C’
E
F
B’
D’
1.在正方形ABCD中,O是对角线AC、BD的交点,过O作 OE⊥OF分别交AB、BC于E、F,若AE=4,CF=3,则AB长为 。
A
E
O
F
D
C
B
拓展延伸
2.将五个边长都为2cm的正方形按如图所示
摆放,点A、B、C分别是正方形的中心,
则图中阴影部分的面积和为 cm2。
A
B
C
D
4
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
设计花坛
综合练习:
1. 如图,在正方形ABCD中,△PBC、△QCD
是两个等边三角形,PB与DQ交于M,BP与CQ
交于E,CP与DQ交于F.求证:PM = QM.
2.如图, 大正方形中有2个小正方形, 如果他们
的面积分别是S1、S2那么S1、S2的大小关
系( )
A、 S1>S2
B、 S1=S2
C、 S1D、 不确定
S1
S2
A
3. 如图,正方形ABCD的面积为12,△ADE是等
边三角形,点E在正方形ABCD内,在对角线AC
上有一点P,使PB+PE的和最小,则这个最小
值为 .
4.如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.
求证:
(1)CE=BG;
(2)CE⊥BG
E
D
F
G
B
C
A
补充练习:
1、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 平方厘米.
A
B
C
D
2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.求证AE=BF;
作业
课后练习题1、2题
正方形的性质
平行四边形
菱形
定义:有一组邻边相等的平行四边形叫做菱形
平行四边形
一个角是直角
矩形
定义:有一个角是直角的平行四边形叫做矩形
邻边相等
正方形的定义 (也是判定方法)
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
平行四边形
矩形
菱形
正方形
正方形的性质
边
对角线
对边平行
四边相等
对角线相等
互相垂直平分
每条对角线平分一组对角
四个角相等且都是直角
角
正方形性质
所以:正方形具有平行四边形、矩形、菱形的一切性质
对称轴
1、判断。
(1)正方形一定是矩形。( )
(2)正方形一定是菱形。( )
(3)菱形一定是正方形。( )
(4)矩形一定是正方形。( )
(5)正方形、矩形、菱形都是平行四边形。( )
√
√
×
×
√
2、在下列性质中,平行四边形具有的是_______,矩形具有的是_________,菱形具有的是___ __ _,正方形具有的是_______________。
(1)四边都相等; (2)对角线互相平分;
(3)对角线相等; (4)对角线互相垂直;
(5)四个角都是直角;
(6)每条对角线平分一组对角;
(7)对边相等且平行;
(8)有两条对称轴。
②⑦
②③⑤⑦⑧
①②④⑥⑦⑧
①②③④⑤⑥⑦
例题1:四边形ABCD是正方形,两条对角线相交于点O,
求∠AOB,∠OAB的度数。
解:∵四边形ABCD是正方形
∴AC⊥BD
∴ ∠AOB=90°
∵四边形ABCD是正方形
∴ ∠BAD=90°
∠BAC= ∠BAD
∴∠OAB=450
A
B
C
D
O
1.正方形两条对角线的和为8cm,它的面积为 。
A
B
C
D
O
E
2.正方形ABCD中,若AC=4,OB=____ ;面积是_______。
3.正方形的面积64cm,则对角线交点到正方形一边的距离______。
4.如图,正方形ABCD中,E是对角线BD上一点。求证:AE=CE。
A
C
B
D
E
如图,正方形ABCD中,E是对角线BD上一点,过点E作EF⊥ BC,EG⊥ CD,垂足为F、G 。求证:AE=FG。
A
C
B
D
F
G
E
例2、如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由。
若将条件“BE=CF”改为”AE⊥BF“,
能否证明”AE=BF”
E
变式一:
如图,在正方形ABCD中,E、P、F三点分别在AB、BC、CD上,且AP⊥EF,AP=5cm,则EF=_____。
A
B
C
D
p
F
G
变式二:
如图,在正方形ABCD中,MN=13,且GH
垂直NM,则GH=_____。
A
B
C
D
G
H
E
M
N
F
例3:AC为正方形ABCD的对角线,E为AC上一点,且AB=AE, EF⊥AC交BC于F. (1)求证:EC=EF=FB
(2)若AC=13,
求△EFC的周长
A
B
C
D
E
F
┌
在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
变式练习 :
G
A
D
C
B
E
F
例4.已知:如图,在正方形ABCD中,E是BC的中点,点F在 CD上,∠FAE=∠BAE,求证:AF=BC+FC
例4.已知:如图,在正方形ABCD中,E是BC的中点,点F在 CD上,∠FAE=∠BAE,求证:AF=BC+FC
G
A
D
C
B
E
F
变式练习:
已知:如图,在正方形ABCD中,E是BC的中点,点F在CD 上,且AE⊥EF
求证:AF=BC+FC
A
D
C
B
E
F
G
∟
G
变式练习:
已知:如图,在正方形ABCD中,E是BC的中点,点F在CD 上,且AE⊥EF
求证:AF=BC+FC
A
D
C
B
E
F
∟
O
A
D
C
B
例5、已知:如图,正方形ABCD的对角线AC、BD相交于点O;正方形A’B’C’D’的顶点A’与点O重合,A’ B’交BC于点E,A’D’交CD于点F,求证:OE=OF
A’
B’
D’
C’
E
F
1
2
3
4
5
(1)观察四边形OECF的面积与正方形ABCD的面积有何关系?
(2)如果将正方形A’B’C’D’换成扇形OB’D’,满足什么条件时上述的关系还成立吗?
A’
B’
D’
C’
E
F
B’
D’
1.在正方形ABCD中,O是对角线AC、BD的交点,过O作 OE⊥OF分别交AB、BC于E、F,若AE=4,CF=3,则AB长为 。
A
E
O
F
D
C
B
拓展延伸
2.将五个边长都为2cm的正方形按如图所示
摆放,点A、B、C分别是正方形的中心,
则图中阴影部分的面积和为 cm2。
A
B
C
D
4
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
设计花坛
综合练习:
1. 如图,在正方形ABCD中,△PBC、△QCD
是两个等边三角形,PB与DQ交于M,BP与CQ
交于E,CP与DQ交于F.求证:PM = QM.
2.如图, 大正方形中有2个小正方形, 如果他们
的面积分别是S1、S2那么S1、S2的大小关
系( )
A、 S1>S2
B、 S1=S2
C、 S1
S1
S2
A
3. 如图,正方形ABCD的面积为12,△ADE是等
边三角形,点E在正方形ABCD内,在对角线AC
上有一点P,使PB+PE的和最小,则这个最小
值为 .
4.如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.
求证:
(1)CE=BG;
(2)CE⊥BG
E
D
F
G
B
C
A
补充练习:
1、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 平方厘米.
A
B
C
D
2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.求证AE=BF;
作业
课后练习题1、2题
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
