2022-2023学年人教版数学九年级下册 26.2 实际问题与反比例函数(1)课件(共23张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学九年级下册 26.2 实际问题与反比例函数(1)课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-11 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
实际问题与反比例函数(1)
知识导入
问题
完成某项任务可以获得元的报酬,参加完成这项任务的人数为(人),人均报酬为(元),那么与之间有什么样的函数关系呢?
人均报酬
建立反比例函数模型解决实际问题.
反比例函数模型
知识精讲
(1)根据题目中的数量关系建立反比例函数模型,求出反比例函数的
解析式;
(2)确定自变量的取值范围;
建立反比例函数模型解决实际问题的步骤:
(3)根据反比例函数的图象和性质解决问题.
典例精讲
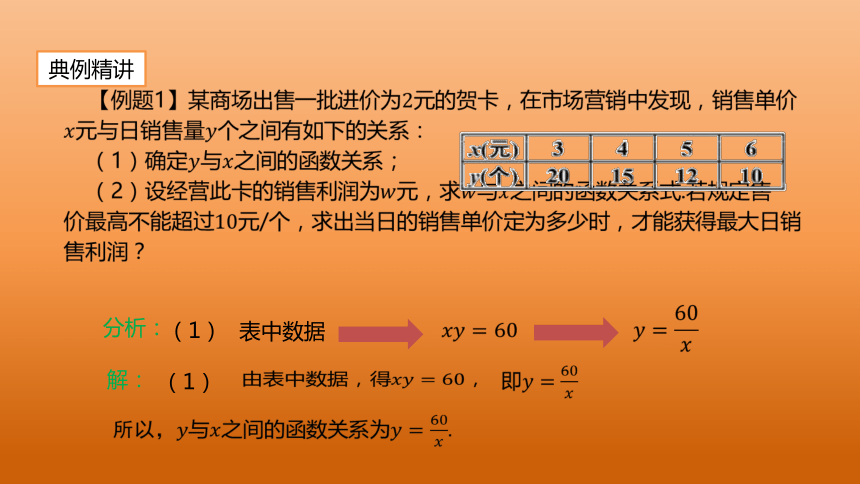
【例题1】某商场出售一批进价为元的贺卡,在市场营销中发现,销售单价元与日销售量个之间有如下的关系:
(1)确定与之间的函数关系;
(2)设经营此卡的销售利润为元,求与之间的函数关系式.若规定售
价最高不能超过元/个,求出当日的销售单价定为多少时,才能获得最大日销售利润?
分析:
(1)
表中数据
解:
(1)
由表中数据,得,
即
所以与之间的函数关系为.
典例精讲
【例题1】某商场出售一批进价为元的贺卡,在市场营销中发现,销售单价元与日销售量个之间有如下的关系:
(2)设经营此卡的销售利润为元,求与之间的函数关系式.若规定售
价最高不能超过元/个,求出当日的销售单价定为多少时,才能获得最大日销售利润?
分析:
(2)
日利润每件利润日销售量
()
典例精讲
解:
(2)
()
函数 在时随着的增大而减小,
∴当时最小,
此时最大.
所以,当日的销售单价定为元/件时,才能获得最大日销售利润.
典例精讲
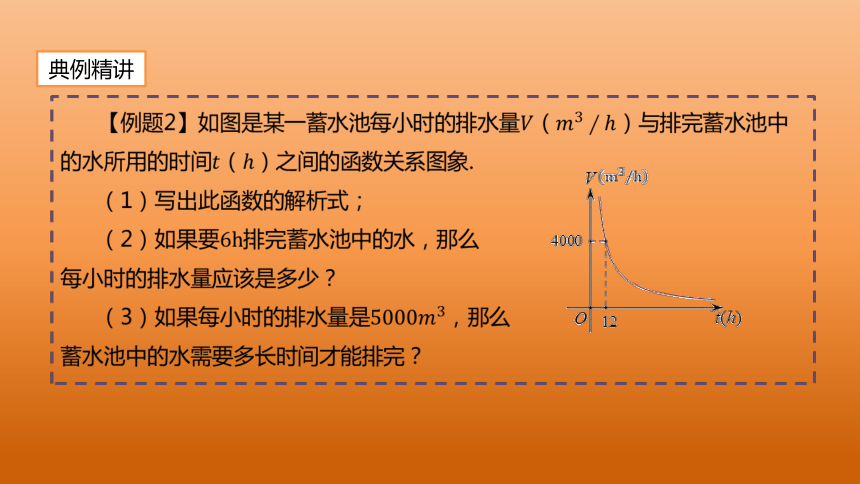
【例题2】如图是某一蓄水池每小时的排水量()与排完蓄水池中的水所用的时间()之间的函数关系图象.
(1)写出此函数的解析式;
(2)如果要排完蓄水池中的水,那么
每小时的排水量应该是多少?
(3)如果每小时的排水量是,那么
蓄水池中的水需要多长时间才能排完?
典例精讲
【例题2】如图是某一蓄水池每小时的排水量()与排完蓄水池中的水所用的时间()之间的函数关系图象.
(1)写出此函数的解析式;
分析:
(1)
每小时的排水量排完水的时间总蓄水量
典例精讲
由图象信息可知,当每小时的排水量
为时,排完蓄水池中的水需要 所以蓄水
池中蓄水量为().
∴ .
解:
(1)
所以函数的解析式为 ().
典例精讲
【例题2】如图是某一蓄水池每小时的排水量()与排完蓄水池中的水所用的时间()之间的函数关系图象.
(2)如果要排完蓄水池中的水,那么
每小时的排水量应该是多少?
分析:
(2)
求出当时,函数的值即可.
典例精讲
解:
(2)
当时,.
所以如果要排完蓄水池中的水,那么每小时的排
水量应该是.
典例精讲
【例题2】如图是某一蓄水池每小时的排水量()与排完蓄水池中的水所用的时间()之间的函数关系图象.
(3)如果每小时的排水量是,那么
蓄水池中的水需要多长时间才能排完?
分析:
(3)
求出当时,函数的值即可.
典例精讲
解:
(3)
当时,.
所以如果每小时的排水量是,那么蓄水池中
的水需要才能排完.
典例精讲
【例题3】工匠制作某种金属工具时要进行材料煅烧(此时材料温度(°)是时间(分钟)的一次函数)和锻造(此时材料温度(°)是时间(分钟)的反比例函数)两个工序,即需要将材料煅烧到,然后停止煅烧进行锻造操作. 从开始到经过分钟时,材料温度降为
已知材料的最初温度是.
(1)求锻造时与的函数关系式,并写
出自变量的取值范围;
(2)根据要求,当材料温度低于
时,须停止操作,那么锻造的时间有多长?
典例精讲
分析:
(1)
(1)求锻造时与的函数关系式,并写出自变量的取值范围.
设锻造时与的函数关系式为.
设
典例精讲
解:
(1)
设锻造时与的函数关系式为.
由图可知在反比例函数的图像上.
∴.
所以锻造时与的函数关系式.
∴.
当时,,
∴.
所以自变量的取值范围是.
典例精讲
分析:
(2)
(2)根据要求,当材料温度低于时,须停止操作,那么锻造的时间有多长?
当时,
锻造时间:(分钟).
当时,,
∴.
因为(分钟),
所以锻造的时间有分钟.
解:
(2)
课堂练习
1.某超市出售一批休闲鞋,进价为元双,经过一段时间的销售发现,日销量(双)是售价(元双)的反比例函数,且当售价为元双时,每日可售出双.
(1)求与的函数关系式;
(2)若超市计划日销售利润为元,则售价应定为多少?
课堂练习
解:
设().
把,代入上式,得,
解得.,
(1)
所以函数解析式为().
(2)
由题意,得(),
即().
解得.
所以售价应定为元.
课堂练习
2.某厂从2013年起开始投入投入技术改进资金,改进后,其产品生产成本不断降低,具体数据如下表:
(1)根据表中的数据,确定你学过的哪种函数能表示其变化规律,说明确定这种函数的理由,并求出解析式;
(2)按照这种规律,若从2017年投入资金万元.
①预计生产成本比2016年降低多少万元?
②若打算在年把每件的成本降低到万元,则还需要投入资金多少万元?
年度 2013 2014 2015 2016
投入资金(万元) 2.5 3 4 4.5
产品成本(万元/件) 7.2 6 4.5 4
课堂练习
解:
(1)
由表中数据知,
反比例函数.
理由为:
所以,.
(2)①当万元时,.
∵(万元).
∴生产成本比2016年降低(万元).
②当时,.
∴.
(万元).
所以,还需要投入资金0.625万元?
本课小结
(1)根据题目中的数量关系建立反比例函数模型,求出反比例函数的
解析式;
(2)确定自变量的取值范围;
建立反比例函数模型解决实际问题的步骤:
(3)根据反比例函数的图象和性质解决问题.
再见
实际问题与反比例函数(1)
知识导入
问题
完成某项任务可以获得元的报酬,参加完成这项任务的人数为(人),人均报酬为(元),那么与之间有什么样的函数关系呢?
人均报酬
建立反比例函数模型解决实际问题.
反比例函数模型
知识精讲
(1)根据题目中的数量关系建立反比例函数模型,求出反比例函数的
解析式;
(2)确定自变量的取值范围;
建立反比例函数模型解决实际问题的步骤:
(3)根据反比例函数的图象和性质解决问题.
典例精讲
【例题1】某商场出售一批进价为元的贺卡,在市场营销中发现,销售单价元与日销售量个之间有如下的关系:
(1)确定与之间的函数关系;
(2)设经营此卡的销售利润为元,求与之间的函数关系式.若规定售
价最高不能超过元/个,求出当日的销售单价定为多少时,才能获得最大日销售利润?
分析:
(1)
表中数据
解:
(1)
由表中数据,得,
即
所以与之间的函数关系为.
典例精讲
【例题1】某商场出售一批进价为元的贺卡,在市场营销中发现,销售单价元与日销售量个之间有如下的关系:
(2)设经营此卡的销售利润为元,求与之间的函数关系式.若规定售
价最高不能超过元/个,求出当日的销售单价定为多少时,才能获得最大日销售利润?
分析:
(2)
日利润每件利润日销售量
()
典例精讲
解:
(2)
()
函数 在时随着的增大而减小,
∴当时最小,
此时最大.
所以,当日的销售单价定为元/件时,才能获得最大日销售利润.
典例精讲
【例题2】如图是某一蓄水池每小时的排水量()与排完蓄水池中的水所用的时间()之间的函数关系图象.
(1)写出此函数的解析式;
(2)如果要排完蓄水池中的水,那么
每小时的排水量应该是多少?
(3)如果每小时的排水量是,那么
蓄水池中的水需要多长时间才能排完?
典例精讲
【例题2】如图是某一蓄水池每小时的排水量()与排完蓄水池中的水所用的时间()之间的函数关系图象.
(1)写出此函数的解析式;
分析:
(1)
每小时的排水量排完水的时间总蓄水量
典例精讲
由图象信息可知,当每小时的排水量
为时,排完蓄水池中的水需要 所以蓄水
池中蓄水量为().
∴ .
解:
(1)
所以函数的解析式为 ().
典例精讲
【例题2】如图是某一蓄水池每小时的排水量()与排完蓄水池中的水所用的时间()之间的函数关系图象.
(2)如果要排完蓄水池中的水,那么
每小时的排水量应该是多少?
分析:
(2)
求出当时,函数的值即可.
典例精讲
解:
(2)
当时,.
所以如果要排完蓄水池中的水,那么每小时的排
水量应该是.
典例精讲
【例题2】如图是某一蓄水池每小时的排水量()与排完蓄水池中的水所用的时间()之间的函数关系图象.
(3)如果每小时的排水量是,那么
蓄水池中的水需要多长时间才能排完?
分析:
(3)
求出当时,函数的值即可.
典例精讲
解:
(3)
当时,.
所以如果每小时的排水量是,那么蓄水池中
的水需要才能排完.
典例精讲
【例题3】工匠制作某种金属工具时要进行材料煅烧(此时材料温度(°)是时间(分钟)的一次函数)和锻造(此时材料温度(°)是时间(分钟)的反比例函数)两个工序,即需要将材料煅烧到,然后停止煅烧进行锻造操作. 从开始到经过分钟时,材料温度降为
已知材料的最初温度是.
(1)求锻造时与的函数关系式,并写
出自变量的取值范围;
(2)根据要求,当材料温度低于
时,须停止操作,那么锻造的时间有多长?
典例精讲
分析:
(1)
(1)求锻造时与的函数关系式,并写出自变量的取值范围.
设锻造时与的函数关系式为.
设
典例精讲
解:
(1)
设锻造时与的函数关系式为.
由图可知在反比例函数的图像上.
∴.
所以锻造时与的函数关系式.
∴.
当时,,
∴.
所以自变量的取值范围是.
典例精讲
分析:
(2)
(2)根据要求,当材料温度低于时,须停止操作,那么锻造的时间有多长?
当时,
锻造时间:(分钟).
当时,,
∴.
因为(分钟),
所以锻造的时间有分钟.
解:
(2)
课堂练习
1.某超市出售一批休闲鞋,进价为元双,经过一段时间的销售发现,日销量(双)是售价(元双)的反比例函数,且当售价为元双时,每日可售出双.
(1)求与的函数关系式;
(2)若超市计划日销售利润为元,则售价应定为多少?
课堂练习
解:
设().
把,代入上式,得,
解得.,
(1)
所以函数解析式为().
(2)
由题意,得(),
即().
解得.
所以售价应定为元.
课堂练习
2.某厂从2013年起开始投入投入技术改进资金,改进后,其产品生产成本不断降低,具体数据如下表:
(1)根据表中的数据,确定你学过的哪种函数能表示其变化规律,说明确定这种函数的理由,并求出解析式;
(2)按照这种规律,若从2017年投入资金万元.
①预计生产成本比2016年降低多少万元?
②若打算在年把每件的成本降低到万元,则还需要投入资金多少万元?
年度 2013 2014 2015 2016
投入资金(万元) 2.5 3 4 4.5
产品成本(万元/件) 7.2 6 4.5 4
课堂练习
解:
(1)
由表中数据知,
反比例函数.
理由为:
所以,.
(2)①当万元时,.
∵(万元).
∴生产成本比2016年降低(万元).
②当时,.
∴.
(万元).
所以,还需要投入资金0.625万元?
本课小结
(1)根据题目中的数量关系建立反比例函数模型,求出反比例函数的
解析式;
(2)确定自变量的取值范围;
建立反比例函数模型解决实际问题的步骤:
(3)根据反比例函数的图象和性质解决问题.
再见
