【新课标】2.5.2一元一次不等式与一次函数 课件(共24张PPT)
文档属性
| 名称 | 【新课标】2.5.2一元一次不等式与一次函数 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 17:33:34 | ||
图片预览








文档简介
(共24张PPT)
2.5.2一元一次不等式与一次函数
北师版八年级下册
教学目标
1 掌握一元一次不等式与一次函数的关系,会运用不等式解决函数有关问题。
2 通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系。
新知导入
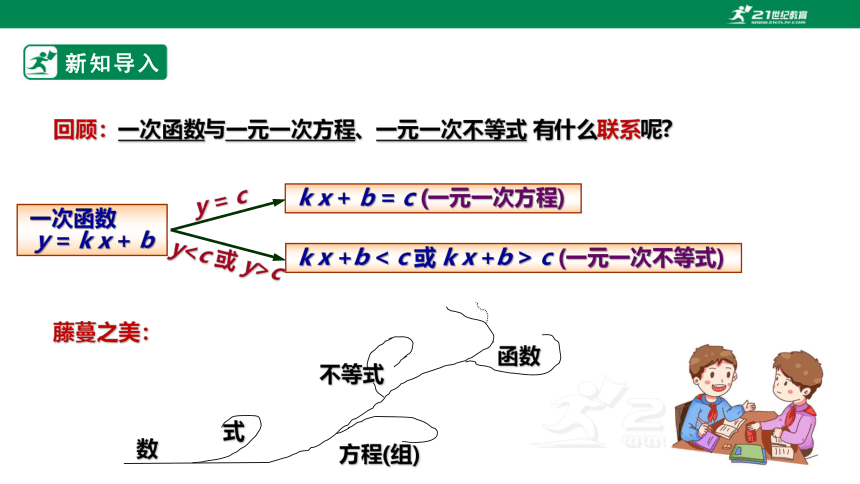
回顾:一次函数与一元一次方程、一元一次不等式 有什么联系呢
一次函数
y = k x + b
y = c
k x + b = c (一元一次方程)
yc
k x +b < c 或 k x +b > c (一元一次不等式)
藤蔓之美:
数
式
方程(组)
不等式
函数
做一做
某电信公司有甲、乙两种手机收费业务.甲种业务规定月租费10元,每通话1分钟收费0.3 元;乙种业务不收月租费,但每通话1分钟收费0.4 元.你认为何时选择甲种业务对顾客更合算?何时选择乙种业务对顾客更合算?
解:设顾客每月通话时长为x 分钟,那么甲种业务每个月的消费额为y1,乙种业务每个月的消费额为y2,根据题意可知
y1=10+0.3x y2=0.4x
新知讲解
① 当y1= y2,得10+0.3x=0.4x,解得x=100;
此时,甲、乙两种业务消费额一样.
②当y1>y2,得10+0.3x>0.4x,解得x<100;
此时,选择乙种业务比较合算.
③当y1100.
此时,选择甲种业务比较合算.
新知讲解
综上可知,
当月通话时长为100分钟时,选择甲种业务和乙种业务对顾客一样;
当月通话时长超过100分钟时,选择甲种业务对顾客更合算;
当月通话时长少于100分钟时,选择乙种业务对顾客更合算
归纳总结
方案选择问题解题思路:
(1)根据题意分别写出不同方案的函数解析式y1、y2;
(2)将方案1、方案2进行比较:①y1=y2 , ②y1y2;从而分别得到自变量的取值范围;
(3)根据实际情况选择方案.
典例精析
例、某单位计划在新年期间组织员工到某地旅游,参加旅游的人数估计为10至25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠.该选择哪一家旅行社呢?
典例精析
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1元,选择乙旅行社时,所需的费用为y2元,由题意得
y2=200×0.8(x-1), 即y2= 160x-160.
y1=200×0.75x, 即y1 = 150x;
典例精析
由y1=y2, 得150x=160x-160, 解得x=16;
由y1>y2, 得150x>160x-160,解得x<16;
由y1<y2, 得150x<160x-160,解得x>16 .
∵ 参加旅游的人数为10至25人,
∴ 当x=16时,甲、乙两家旅行社的收费相同;
当16当10≤x<16时,选择乙旅行社费用较少.
能用一次函数解答吗?
做一做
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1元,选择乙旅行社时,所需的费用为y2元,由题意得
y2=200×0.8(x-1), 即y2= 160x-160.
y1=200×0.75x, 即y1 = 150x;
在同一平面直角坐标系中画出直线y1=150x和y2=160x-160.
0
5
10
15
20
25
x
y2=160x-160
y1=150x
1500
500
1000
y
2000
2500
3000
3500
4000
新知讲解
令y1=y2两直线的交点坐标为(16,2400)
当x=16时, 甲、乙两家旅行社的收费相同;
当16当10≤x<16时,y1>y2,选择乙旅行社费用较少.
观察图象可知:
新知讲解
在本节问题中,一次函数刻画了问题中两个变量之间存在的一种相互依赖关系,而一元一次不等式则描述了问题中这两个变量满足某些特定条件时的状态.因此,可以从一次函数的角度解决一元一次不等式的问题,也可以利用一元一次不等式解决一次函数的相关问题
归纳总结
代数法:
1. 根据题意分别写出方案A、B的函数解析式yA、yB;
2. 将方案A、B进行比较:①yA>yB , ②yA3. 根据实际情况选择方案.
图象法:
1. 根据题意分别写出方案A、B的函数解析式yA、yB;
2. 在同一平面直角坐标系中画出两个一次函数的图象.
3. 确定两直线的交点坐标.
4. 确定符合条件的图象的横坐标的取值范围.
5. 根据实际情况选择方案.
方案选择问题方法和步骤:
课堂练习
1. 如图所示,某单位准备和一个体车主或一国营出租车
公司中的一家签订月租车合同,设汽车每月行驶x千米,
个体车主收费y1元,国营出租车公司收费为y2元,观察图
象可知,当 时,选用个体车较合算( )
A.x<1500 B.x=1500 C.x>1200 D.x>1500
D
课堂练习
2.某公司准备与汽车租赁公司签订租车合同,以每月用车路程为x km计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元,若y1,y2与x之间的函数关系如图所示,其中x=0对应的函数值为月固定租赁费,则下列判断错误的是( )
A.当月用车路程为2 000 km时,两家汽车租赁公司收取的租赁费用相同
B.当月用车路程为2 300 km时,租赁乙汽车租赁公司的车比较合算
C.除去月固定租赁费,甲租赁公司平均每
千米收取的费用比乙租赁公司多
D.除去月固定租赁费,甲租赁公司平均每
千米收取的费用比乙租赁公司少
D
课堂练习
3.节能灯越来越受到人们的喜爱,一种白炽灯和一种节能灯的使用费用与照明时间x之间的函数关系式分别为:当使用时间超过______小时,节能灯的使用费用低于白炽灯的使用费用。
4. 如图所示,是某电信公司甲、乙两种业务:每月通话费用y(元)与通话时间x(分钟)之间的函数关系.某企业的周经理想从两种业务中选择一种,如果周经理每个月的通话时间都在100分钟以上,那么选择_______种业务合算.
1000
甲
课堂练习
5.某公司40名员工到一景点参观,景点门票为30元/人.该景点规定满40人可以购买团体票,票价打八折.这天恰逢妇女节,该景点做活动,女士票价打五折,但不能同时享受两种优惠.请你帮助他们选择购票方案.
解:设该公司参观者中有女士x人,选择购买女士打五折票时,所需费用为y1元,选择购买团体票时,所需的费用为y2元,则
y1 = 30×0.5x +30×(40-x)= -15x +1200;
y2 = 30×40×0.8= 960.
当y1 = y2时,-15x +1200= 960,解得x = 16;
当y1 > y2时,-15x +1200 > 960,解得x < 16;
当y1 < y2时,-15x +1200 < 960,解得x > 16.
课堂练习
所以当女士不足16(0 < x <16)人时,选择购买团体票合算;
当女士恰好是16(x = 16)人时,选择两种方案所需费用相同;
当女士多于16(16 < x ≤ 40)人时,选择购买女士打五折票合算.
课堂总结
实际问题
写出两个函数表达式
不等式
解不等式
画出图象
分析图象
解决问题
板书设计
课题:2.5.2 一元一次不等式与一次函数
1、方案选择问题
2、解决优化方案问题的一般步骤.
作业布置
【必做题】
教材第53页习题2.7的1、2
【选做题】
教材第53页习题2.7的3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.5.2一元一次不等式与一次函数
北师版八年级下册
教学目标
1 掌握一元一次不等式与一次函数的关系,会运用不等式解决函数有关问题。
2 通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系。
新知导入
回顾:一次函数与一元一次方程、一元一次不等式 有什么联系呢
一次函数
y = k x + b
y = c
k x + b = c (一元一次方程)
y
k x +b < c 或 k x +b > c (一元一次不等式)
藤蔓之美:
数
式
方程(组)
不等式
函数
做一做
某电信公司有甲、乙两种手机收费业务.甲种业务规定月租费10元,每通话1分钟收费0.3 元;乙种业务不收月租费,但每通话1分钟收费0.4 元.你认为何时选择甲种业务对顾客更合算?何时选择乙种业务对顾客更合算?
解:设顾客每月通话时长为x 分钟,那么甲种业务每个月的消费额为y1,乙种业务每个月的消费额为y2,根据题意可知
y1=10+0.3x y2=0.4x
新知讲解
① 当y1= y2,得10+0.3x=0.4x,解得x=100;
此时,甲、乙两种业务消费额一样.
②当y1>y2,得10+0.3x>0.4x,解得x<100;
此时,选择乙种业务比较合算.
③当y1
此时,选择甲种业务比较合算.
新知讲解
综上可知,
当月通话时长为100分钟时,选择甲种业务和乙种业务对顾客一样;
当月通话时长超过100分钟时,选择甲种业务对顾客更合算;
当月通话时长少于100分钟时,选择乙种业务对顾客更合算
归纳总结
方案选择问题解题思路:
(1)根据题意分别写出不同方案的函数解析式y1、y2;
(2)将方案1、方案2进行比较:①y1=y2 , ②y1
(3)根据实际情况选择方案.
典例精析
例、某单位计划在新年期间组织员工到某地旅游,参加旅游的人数估计为10至25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠.该选择哪一家旅行社呢?
典例精析
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1元,选择乙旅行社时,所需的费用为y2元,由题意得
y2=200×0.8(x-1), 即y2= 160x-160.
y1=200×0.75x, 即y1 = 150x;
典例精析
由y1=y2, 得150x=160x-160, 解得x=16;
由y1>y2, 得150x>160x-160,解得x<16;
由y1<y2, 得150x<160x-160,解得x>16 .
∵ 参加旅游的人数为10至25人,
∴ 当x=16时,甲、乙两家旅行社的收费相同;
当16
能用一次函数解答吗?
做一做
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1元,选择乙旅行社时,所需的费用为y2元,由题意得
y2=200×0.8(x-1), 即y2= 160x-160.
y1=200×0.75x, 即y1 = 150x;
在同一平面直角坐标系中画出直线y1=150x和y2=160x-160.
0
5
10
15
20
25
x
y2=160x-160
y1=150x
1500
500
1000
y
2000
2500
3000
3500
4000
新知讲解
令y1=y2两直线的交点坐标为(16,2400)
当x=16时, 甲、乙两家旅行社的收费相同;
当16
观察图象可知:
新知讲解
在本节问题中,一次函数刻画了问题中两个变量之间存在的一种相互依赖关系,而一元一次不等式则描述了问题中这两个变量满足某些特定条件时的状态.因此,可以从一次函数的角度解决一元一次不等式的问题,也可以利用一元一次不等式解决一次函数的相关问题
归纳总结
代数法:
1. 根据题意分别写出方案A、B的函数解析式yA、yB;
2. 将方案A、B进行比较:①yA>yB , ②yA
图象法:
1. 根据题意分别写出方案A、B的函数解析式yA、yB;
2. 在同一平面直角坐标系中画出两个一次函数的图象.
3. 确定两直线的交点坐标.
4. 确定符合条件的图象的横坐标的取值范围.
5. 根据实际情况选择方案.
方案选择问题方法和步骤:
课堂练习
1. 如图所示,某单位准备和一个体车主或一国营出租车
公司中的一家签订月租车合同,设汽车每月行驶x千米,
个体车主收费y1元,国营出租车公司收费为y2元,观察图
象可知,当 时,选用个体车较合算( )
A.x<1500 B.x=1500 C.x>1200 D.x>1500
D
课堂练习
2.某公司准备与汽车租赁公司签订租车合同,以每月用车路程为x km计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元,若y1,y2与x之间的函数关系如图所示,其中x=0对应的函数值为月固定租赁费,则下列判断错误的是( )
A.当月用车路程为2 000 km时,两家汽车租赁公司收取的租赁费用相同
B.当月用车路程为2 300 km时,租赁乙汽车租赁公司的车比较合算
C.除去月固定租赁费,甲租赁公司平均每
千米收取的费用比乙租赁公司多
D.除去月固定租赁费,甲租赁公司平均每
千米收取的费用比乙租赁公司少
D
课堂练习
3.节能灯越来越受到人们的喜爱,一种白炽灯和一种节能灯的使用费用与照明时间x之间的函数关系式分别为:当使用时间超过______小时,节能灯的使用费用低于白炽灯的使用费用。
4. 如图所示,是某电信公司甲、乙两种业务:每月通话费用y(元)与通话时间x(分钟)之间的函数关系.某企业的周经理想从两种业务中选择一种,如果周经理每个月的通话时间都在100分钟以上,那么选择_______种业务合算.
1000
甲
课堂练习
5.某公司40名员工到一景点参观,景点门票为30元/人.该景点规定满40人可以购买团体票,票价打八折.这天恰逢妇女节,该景点做活动,女士票价打五折,但不能同时享受两种优惠.请你帮助他们选择购票方案.
解:设该公司参观者中有女士x人,选择购买女士打五折票时,所需费用为y1元,选择购买团体票时,所需的费用为y2元,则
y1 = 30×0.5x +30×(40-x)= -15x +1200;
y2 = 30×40×0.8= 960.
当y1 = y2时,-15x +1200= 960,解得x = 16;
当y1 > y2时,-15x +1200 > 960,解得x < 16;
当y1 < y2时,-15x +1200 < 960,解得x > 16.
课堂练习
所以当女士不足16(0 < x <16)人时,选择购买团体票合算;
当女士恰好是16(x = 16)人时,选择两种方案所需费用相同;
当女士多于16(16 < x ≤ 40)人时,选择购买女士打五折票合算.
课堂总结
实际问题
写出两个函数表达式
不等式
解不等式
画出图象
分析图象
解决问题
板书设计
课题:2.5.2 一元一次不等式与一次函数
1、方案选择问题
2、解决优化方案问题的一般步骤.
作业布置
【必做题】
教材第53页习题2.7的1、2
【选做题】
教材第53页习题2.7的3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
