2022-2023学年人教版七年级数学下册7.2坐标方法的简单应用同步练习 (含解析)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册7.2坐标方法的简单应用同步练习 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 182.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-11 00:00:00 | ||
图片预览




文档简介
2023年七年级下册 数学第七章【同步测试】+【课后提升】
7.2坐标方法的简单应用
同步测试阶段:
一、单选题
1.已知线段CD是由线段AB平移得到的,点A(﹣1,2)的对应点为C(3,1),则点B(﹣2,﹣2)的对应点D的坐标为( )
A.(7,﹣1) B.(7,﹣3) C.(2,﹣3) D.(2,﹣1)
2.根据下列表述,能确定具体位置是( )
A.某电影院2排 B.金寨南路
C.北偏东 D.东经 ,北纬
3.如图所示,与①中的三角形相比,②中的三角形发生的变化是( )
A.向左平移3个单位 B.向左平移1个单位
C.向上平移3个单位 D.向下平移1个单位
4.在平面直角坐标系中,将点 向右平移 个单位长度后得到点的坐标为 ,则 的值为( )
A.1 B.3 C.5 D.14
5.若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )
A.(﹣2,﹣1) B.(﹣1,0)
C.(﹣1,﹣1) D.(﹣2,0)
二、填空题
6.在平面直角坐标系中,将点 向左平移4个单位长度,再向上平移2个单位长度得到点 的坐标为 .
7.如果将点A(-3,2)向右移1个单位长度再向下平移2个单位长度单位得到点B,那么点B的坐标是 .
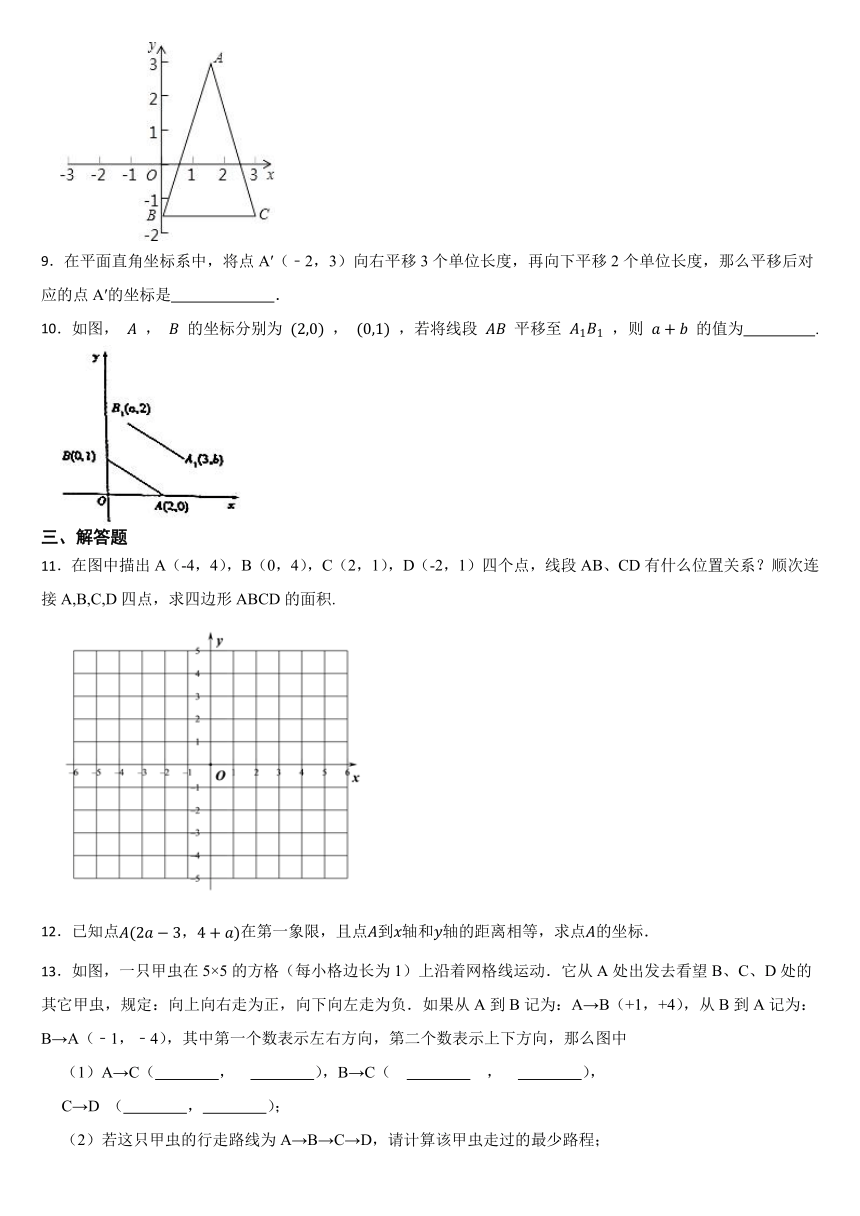
8.如图,已知等腰三角形ABC中,顶点A的坐标是( ,3),点B的坐标是(0,﹣2),BC∥x轴,则点C的坐标是 .
9.在平面直角坐标系中,将点A′(﹣2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是 .
10.如图, , 的坐标分别为 , ,若将线段 平移至 ,则 的值为 .
三、解答题
11.在图中描出A(-4,4),B(0,4),C(2,1),D(-2,1)四个点,线段AB、CD有什么位置关系?顺次连接A,B,C,D四点,求四边形ABCD的面积.
12.已知点在第一象限,且点到轴和轴的距离相等,求点的坐标.
13.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→C( , ),
C→D ( , );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的最少路程;
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置.
14.如图,在三角形ABC中,B(2,0),把三角形ABC沿AC边平移,使A点到C点,三角形ABC变换为三角形CED,已知C(0,3.5),请写出A,D,E的坐标,并说出平移的过程.
课后提升阶段:
一、单选题
1.将直角坐标系中的点(-1,-3)向上平移4个单位,再向左平移3个单位后的点的坐标为( )
A.(3,-1) B.(3,-6) C.(-4,1) D.(1,0)
2.在平面直角坐标系内,把点P(-2,1)向右平移一个单位,则得到的对应点P′的坐标是( )
A.(-2,2) B.(-1,1) C.(-3,1) D.(-2,0)
3.点A(﹣3,﹣5)向左平移3个单位,再向上平移4个单位到点B,则点B的坐标为( )
A.(1,﹣8) B.(1,﹣2)
C.(﹣6,﹣1) D.(0,﹣1)
4.如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示国旗杆的点的坐标为(0,2.5),表示中国国家博物馆的点的坐标为(4,1),则表示下列建筑的点的坐标正确的是( )
A.天安门(0,4) B.人民大会堂(﹣4,1)
C.毛主席纪念堂(﹣1,﹣3) D.正阳门(0,﹣5)
5.在平面直角坐标系中,点P(﹣2,3)向右平移3个单位长度后的坐标为( )
A.(3,6) B.(1,3) C.(1,6) D.(6,6)
二、填空题
6.把点 先向右平移2个单位,再向上平移3个单位,所得点的坐标为 .
7.有了平面直角坐标系,平面内的点可以用 来表示;同样一个点的坐标确定了该点在坐标平面内的 .
8.已知直线AB∥x轴,A点的坐标为(2,1),并且线段AB=2,则点B的坐标为
9.三角形ABC的三个顶点A(1,2),B(-1,-2),C(-2,3),将其平移到点A′(-1,-2)处,且使A与A′重合,则B、C两点对应点的坐标分别为 , .
10.在平面直角坐标系中,点 在第 象限.
三、解答题
11.已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
(1)A点的坐标为 ; B点的坐标为 ;C点的坐标为 .
(2)将点A、B、C的横坐标保持不变,纵坐标分别乘以-1,分别得点A'、B'、C',并连接A'、B'、C'得△A' B' C',请画出△A' B' C'.
(3)△A' B' C'与△ABC的位置关系是 .
12.如图所示,求出A,B,C,D,E,F,O点的坐标.
13.如图所示,△ABO中,A,B两点的坐标分别为(2,4),(7,2),C,G,F,E分别为过A,B两点所作的y轴、x轴的垂线与y轴、x轴的交点.求△AOB的面积.
14.如图的方格中有25个汉字,如四1表示“天”,请沿着以下路径去寻找你的礼物:
(1)一1→三2→二4→四3→五1
(2)五3→二1→二3→一5→三4
(3)四5→四1→一2→三3→五2.
同步测试答案:
1.【答案】C
【解析】【解答】解:由点A(﹣1,2)的对应点为C(3,1),
知线段AB向右平移4个单位、向下平移1个单位即可得到CD,
∴点B(﹣2,﹣2)的对应点D的坐标为(﹣2+4,﹣2﹣1),即(2,﹣3),
故答案为:C.
【分析】由点A(﹣1,2)的对应点为C(3,1),知线段AB向右平移4个单位、向下平移1个单位即可得到CD,因此可得点B平移后的对应点的坐标。
2.【答案】D
【解析】【解答】A. 某电影院2排,不能确定具体位置,故本选项不符合题意;
B. 金寨南路,不能确定具体位置,故本选项不符合题意;
C. 北偏东 ,不能确定具体位置,故本选项不符合题意;
D. 东经 ,北纬 ,能确定具体位置,故本选项符合题意.
故答案为:D.
【分析】根据有序数对确定地理位置,对各选项分析即可.
3.【答案】A
【解析】【解答】解:由图①到图②,点(1,1)平移到点(-2,1),
点(3,1)平移到点(0,1),都是向左平移3个单位,
故图形平移规律为:①中的三角形向左平移3个单位.
故答案为:A.
【分析】观察图形,可知点(1,1)平移到点(-2,1),可知横纵坐标由1变到-2,横坐标变化是左右平移,左减右加(横坐标加或减),即可得出答案。
4.【答案】C
【解析】【解答】解:∵点P(n-2,2n+4),
∴向右平移m个单位长度可得 ,
∵P′(4,6),
∴n-2+m=4,2n+4=6,
解得:n=1,m=5
故答案为:C.
【分析】根据横坐标、右移加,左移减可得点P(n-2,2n+4)向右平移m个单位长度可得 ,进而得n-2+m=4,2n+4=6,再解方程即可。
5.【答案】C
【解析】【解答】解:∵点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,
∴点B的横坐标为1﹣2=﹣1,纵坐标为3﹣4=﹣1,
∴B的坐标为(﹣1,﹣1).
故选C.
【分析】根据向左平移横坐标减,向下平移纵坐标减求解即可.本题考查了坐标与图形变化﹣平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
6.【答案】
【解析】【解答】解:将点P(3,3)向左平移4个单位长度,再向上平移2个单位长度得到点 的坐标是(3-4,3+2),即(-1,5).
故答案为: .
【分析】根据向左平移横坐标减,向上平移纵坐标加即可得解.
7.【答案】(-2,0)
【解析】【解答】解:将点A(-3,2)向右移1个单位长度再向下平移2个单位长度单位得到点B(-2,0),
故答案为:(-2,0).
【分析】利用点坐标平移的特征:左减右加,上加下减求解即可。
8.【答案】(3,﹣2)
【解析】【解答】解:∵BC∥x轴
∴B、C两点纵坐标相同,都是﹣2
过A点作AD⊥BC,垂足为D,则D( ,﹣2)
∵直线AD为△ABC的对称轴,由对称性可知点C的横坐标是3
∴C(3,﹣2)
【分析】根据平行于x轴的直线上的点的纵坐标相同得出:B、C两点纵坐标相同,都是﹣2,过A点作AD⊥BC,垂足为D,根据垂直于x轴的直线上的点的横坐标相同及平行于x轴的直线上的点的纵坐标相同得出D点的坐标,根据等腰三角形的对称性得出CD=BD,进而得出BC的长,从而得出C点的坐标。
9.【答案】(1,1)
【解析】【解答】解:∵将点A′(-2,3)向右平移3个单位长度,
∴得到(1,3),
∵再向下平移2个单位长度,
∴平移后对应的点A′的坐标是:(1,1).
故答案为:(1,1).
【分析】根据点的平移规律:左减右加(横坐标减或加),上加下减(纵坐标加 或减),就可求出平移后对应的点A′的坐标。
10.【答案】2
【解析】【解答】解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,
由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,
所以点A. B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2. 故答案为:2
【分析】直接利用平移中点的变化规律求解即可.
11.【答案】解:(1)画出图形直接得到AB∥x轴,DC∥x轴,所以AB∥CD;(2)S=4×3=12
【解析】【分析】先在平面直角坐标系中描点、连线,画出图形。然后证明这是一个平行四边形,从而求出平行四边形ABCD的面积=底×高。
12.【答案】解:点在第一象限,点到轴和轴的距离相等,
,
解得:,
故,,
则点的坐标为:.
【解析】【分析】根据第一象限的点横坐标与纵坐标都是正数及一个点到x轴的距离等于其纵坐标的绝对值,到y轴的距离等于其横坐标的绝对值,可得2a-3=4+a,求出a的值,然后求出2a-3、4+a的值,据此可得点A的坐标.
13.【答案】解:(1)A→C(+3,+4),B→C(+2,0),C→D(+1,﹣2);
(2)1+4+2+1+2=10;
(3)点P如图所示.
【解析】【分析】(1)根据第一个数表示左右方向,第二个数表示上下方向结合图形写出即可;
(2)根据行走路线列出算式计算即可得解;
(3)根据方格和标记方法作出线路图即可得解.
14.【答案】解:由图象知:A(﹣2,0),D(2,7),E(2,3.5),
把△ABC向右平移2个单位长度,向上平移3.5个单位长度得到△CED.
【解析】【分析】根据网格结构和平移的性质即可得到结论.
课后提升答案:
1.【答案】C
【解析】【解答】解:由点(-1,-3)向上平移4个单位,再向左平移3个单位后的点的坐标为 .
故答案为:C.
【分析】根据平移的点的坐标变化特征“左减右加、上加下减”可求解.
2.【答案】B
【解析】【分析】根据平移时,点的坐标变化规律“上加下减,左减右加”进行计算.
【解答】根据题意,从点P到点P′,点P′的纵坐标不变,横坐标是-2+1=-1,
故点P′的坐标是(-1,1).
故选B.
3.【答案】C
【解析】【解答】解:∵点A(﹣3,﹣5)向左平移3个单位,再向上平移4个单位到点B,
∴点B的坐标为(﹣3﹣3,﹣5+4),即(﹣6,﹣1).
故选C.
【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
4.【答案】B
【解析】【解答】解:建立平面直角坐标系如图所示,
天安门(0,5),人民大会堂(﹣4,1),毛主席纪念堂(0,﹣3),正阳门(0,﹣5.5),
所以,建筑的点的坐标正确的是人民大会堂.
故选B.
【分析】以中国国家博物馆的位置向左4个单位,向下1个单位为坐标原点建立平面直角坐标系,然后写出各建筑点的坐标,从而得解.
5.【答案】B
【解析】【解答】解:平移后的横坐标为﹣2+3=1,
纵坐标为3,
∴点P(﹣2,3)向右平移3个单位长度后的坐标为(1,3),
故答案为:B.
【分析】让横坐标加3,纵坐标不变即可得到所求的坐标.
6.【答案】(5,2)
【解析】【解答】解:点 先向右平移2个单位,再向上平移3个单位,所得点的坐标为(5,2)
故答案为:(5,2).
【分析】根据坐标的平移特点“左减右加,上加下减”即可求解.
7.【答案】坐标;位置
【解析】【解答】有了平面直角坐标系,平面内的点可以用坐标来表示;同样一个点的坐标确定了该点在坐标平面内的位置.
故答案为:坐标;位置.
【分析】在平面直角坐标系中,要用两个数据才能表示一个点的位置,据此填空即可.
8.【答案】(4,1)或(0,1)
【解析】【解答】解:∵AB∥x轴,点A坐标为(2,1),
∴A,B的纵坐标相等为1,
设点B的横坐标为x,则有AB=|x 2|=2,
解得:x=4或0,
∴点B的坐标为(4,1)或(0,1),
故答案为:(4,1)或(0,1).
【分析】AB∥x轴,说明A,B的纵坐标相等为1,再根据两点之间的距离公式求解即可.
9.【答案】(-3,-6);(-4,-1)
【解析】【解答】根据题意可知使点A到点A′ ,所以△ABC是先向左平移2个单位长度,再向下平移4个单位长度,所以点B,C的横坐标分别减2,纵坐标分别减4,即点B、C平移后对应点的坐标分别为(-3,-6),(-4,-1).
【分析】本题先根据点A的平移确定平移方式,再求出点B,C平移后对应点的坐标.
10.【答案】四
【解析】【解答】解:点P(3,-4)在第四象限.
11.【答案】(1)(-2,3);(-6,0);(-1,0)
(2)解:如图所示:
(3)关于x轴对称
【解析】【解答】(1)A点的坐标为(-2,3);B点的坐标为(-6,0);C点的坐标为(-1,0).(3)关于x轴对称.
【分析】(1)由平面直角坐标系的图象可以写出A、B、C坐标;
(2)先由ΔABC的纵坐标乘以-1,然后在平面直角坐标系中描出各点即可画出ΔA'B'C';
(3)由图象可以看出,两个三角形关于x轴对称。
12.【答案】解:由图中坐标系可知各点的坐标为:A(﹣2,0),B(2,0),C(1,2),D(0,4),E(﹣1,2),F(0,2),
O(0,0).
【解析】【分析】直接根据图示,在网格中数出对应的点的坐标即可.
13.【答案】解:∵A(2,4),B(7,2),
∴AC=2、CO=4、OE=7、BE=2、AF=4、EF=OE﹣OF=7﹣2=5,
由图可知,S△AOB=S矩形ACOF+S梯形AFEB﹣S△ACO﹣S△BOE,
=2×4+(2+4)×5﹣×2×4﹣×7×2,
=8+15﹣4﹣7,
=23﹣11,
=12.
【解析】【分析】根据点A、B的坐标求出AC、CO、OE、BE、AF、EF的长度,然后根据S△AOB=S矩形ACOF+S梯形AFEB﹣S△ACO﹣S△BOE列式计算即可得解.
14.【答案】解:(1)一1表示我,三2表示是,二4表示最,四3表示棒,五1表示的,所以礼物为:我是最棒的;(2)五3表示努,二1表示力,二3表示就,一5表示能,三4行,所以礼物为:努力就能行;(3)四5表示明,四1表示天,一2表示会,三3表示更,五2表示好,所以礼物为:明天会更好.
【解析】【分析】(1)根据表格,分别找出一1→三2→二4→四3→五1表示的汉字,排列即可;
(2)根据表格,分别找出五3→二1→二3→一5→三4表示的汉字,排列即可;
(3)根据表格,分别找出四5→四1→一2→三3→五2表示的汉字,排列即可.
7.2坐标方法的简单应用
同步测试阶段:
一、单选题
1.已知线段CD是由线段AB平移得到的,点A(﹣1,2)的对应点为C(3,1),则点B(﹣2,﹣2)的对应点D的坐标为( )
A.(7,﹣1) B.(7,﹣3) C.(2,﹣3) D.(2,﹣1)
2.根据下列表述,能确定具体位置是( )
A.某电影院2排 B.金寨南路
C.北偏东 D.东经 ,北纬
3.如图所示,与①中的三角形相比,②中的三角形发生的变化是( )
A.向左平移3个单位 B.向左平移1个单位
C.向上平移3个单位 D.向下平移1个单位
4.在平面直角坐标系中,将点 向右平移 个单位长度后得到点的坐标为 ,则 的值为( )
A.1 B.3 C.5 D.14
5.若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )
A.(﹣2,﹣1) B.(﹣1,0)
C.(﹣1,﹣1) D.(﹣2,0)
二、填空题
6.在平面直角坐标系中,将点 向左平移4个单位长度,再向上平移2个单位长度得到点 的坐标为 .
7.如果将点A(-3,2)向右移1个单位长度再向下平移2个单位长度单位得到点B,那么点B的坐标是 .
8.如图,已知等腰三角形ABC中,顶点A的坐标是( ,3),点B的坐标是(0,﹣2),BC∥x轴,则点C的坐标是 .
9.在平面直角坐标系中,将点A′(﹣2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是 .
10.如图, , 的坐标分别为 , ,若将线段 平移至 ,则 的值为 .
三、解答题
11.在图中描出A(-4,4),B(0,4),C(2,1),D(-2,1)四个点,线段AB、CD有什么位置关系?顺次连接A,B,C,D四点,求四边形ABCD的面积.
12.已知点在第一象限,且点到轴和轴的距离相等,求点的坐标.
13.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→C( , ),
C→D ( , );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的最少路程;
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置.
14.如图,在三角形ABC中,B(2,0),把三角形ABC沿AC边平移,使A点到C点,三角形ABC变换为三角形CED,已知C(0,3.5),请写出A,D,E的坐标,并说出平移的过程.
课后提升阶段:
一、单选题
1.将直角坐标系中的点(-1,-3)向上平移4个单位,再向左平移3个单位后的点的坐标为( )
A.(3,-1) B.(3,-6) C.(-4,1) D.(1,0)
2.在平面直角坐标系内,把点P(-2,1)向右平移一个单位,则得到的对应点P′的坐标是( )
A.(-2,2) B.(-1,1) C.(-3,1) D.(-2,0)
3.点A(﹣3,﹣5)向左平移3个单位,再向上平移4个单位到点B,则点B的坐标为( )
A.(1,﹣8) B.(1,﹣2)
C.(﹣6,﹣1) D.(0,﹣1)
4.如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示国旗杆的点的坐标为(0,2.5),表示中国国家博物馆的点的坐标为(4,1),则表示下列建筑的点的坐标正确的是( )
A.天安门(0,4) B.人民大会堂(﹣4,1)
C.毛主席纪念堂(﹣1,﹣3) D.正阳门(0,﹣5)
5.在平面直角坐标系中,点P(﹣2,3)向右平移3个单位长度后的坐标为( )
A.(3,6) B.(1,3) C.(1,6) D.(6,6)
二、填空题
6.把点 先向右平移2个单位,再向上平移3个单位,所得点的坐标为 .
7.有了平面直角坐标系,平面内的点可以用 来表示;同样一个点的坐标确定了该点在坐标平面内的 .
8.已知直线AB∥x轴,A点的坐标为(2,1),并且线段AB=2,则点B的坐标为
9.三角形ABC的三个顶点A(1,2),B(-1,-2),C(-2,3),将其平移到点A′(-1,-2)处,且使A与A′重合,则B、C两点对应点的坐标分别为 , .
10.在平面直角坐标系中,点 在第 象限.
三、解答题
11.已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
(1)A点的坐标为 ; B点的坐标为 ;C点的坐标为 .
(2)将点A、B、C的横坐标保持不变,纵坐标分别乘以-1,分别得点A'、B'、C',并连接A'、B'、C'得△A' B' C',请画出△A' B' C'.
(3)△A' B' C'与△ABC的位置关系是 .
12.如图所示,求出A,B,C,D,E,F,O点的坐标.
13.如图所示,△ABO中,A,B两点的坐标分别为(2,4),(7,2),C,G,F,E分别为过A,B两点所作的y轴、x轴的垂线与y轴、x轴的交点.求△AOB的面积.
14.如图的方格中有25个汉字,如四1表示“天”,请沿着以下路径去寻找你的礼物:
(1)一1→三2→二4→四3→五1
(2)五3→二1→二3→一5→三4
(3)四5→四1→一2→三3→五2.
同步测试答案:
1.【答案】C
【解析】【解答】解:由点A(﹣1,2)的对应点为C(3,1),
知线段AB向右平移4个单位、向下平移1个单位即可得到CD,
∴点B(﹣2,﹣2)的对应点D的坐标为(﹣2+4,﹣2﹣1),即(2,﹣3),
故答案为:C.
【分析】由点A(﹣1,2)的对应点为C(3,1),知线段AB向右平移4个单位、向下平移1个单位即可得到CD,因此可得点B平移后的对应点的坐标。
2.【答案】D
【解析】【解答】A. 某电影院2排,不能确定具体位置,故本选项不符合题意;
B. 金寨南路,不能确定具体位置,故本选项不符合题意;
C. 北偏东 ,不能确定具体位置,故本选项不符合题意;
D. 东经 ,北纬 ,能确定具体位置,故本选项符合题意.
故答案为:D.
【分析】根据有序数对确定地理位置,对各选项分析即可.
3.【答案】A
【解析】【解答】解:由图①到图②,点(1,1)平移到点(-2,1),
点(3,1)平移到点(0,1),都是向左平移3个单位,
故图形平移规律为:①中的三角形向左平移3个单位.
故答案为:A.
【分析】观察图形,可知点(1,1)平移到点(-2,1),可知横纵坐标由1变到-2,横坐标变化是左右平移,左减右加(横坐标加或减),即可得出答案。
4.【答案】C
【解析】【解答】解:∵点P(n-2,2n+4),
∴向右平移m个单位长度可得 ,
∵P′(4,6),
∴n-2+m=4,2n+4=6,
解得:n=1,m=5
故答案为:C.
【分析】根据横坐标、右移加,左移减可得点P(n-2,2n+4)向右平移m个单位长度可得 ,进而得n-2+m=4,2n+4=6,再解方程即可。
5.【答案】C
【解析】【解答】解:∵点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,
∴点B的横坐标为1﹣2=﹣1,纵坐标为3﹣4=﹣1,
∴B的坐标为(﹣1,﹣1).
故选C.
【分析】根据向左平移横坐标减,向下平移纵坐标减求解即可.本题考查了坐标与图形变化﹣平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
6.【答案】
【解析】【解答】解:将点P(3,3)向左平移4个单位长度,再向上平移2个单位长度得到点 的坐标是(3-4,3+2),即(-1,5).
故答案为: .
【分析】根据向左平移横坐标减,向上平移纵坐标加即可得解.
7.【答案】(-2,0)
【解析】【解答】解:将点A(-3,2)向右移1个单位长度再向下平移2个单位长度单位得到点B(-2,0),
故答案为:(-2,0).
【分析】利用点坐标平移的特征:左减右加,上加下减求解即可。
8.【答案】(3,﹣2)
【解析】【解答】解:∵BC∥x轴
∴B、C两点纵坐标相同,都是﹣2
过A点作AD⊥BC,垂足为D,则D( ,﹣2)
∵直线AD为△ABC的对称轴,由对称性可知点C的横坐标是3
∴C(3,﹣2)
【分析】根据平行于x轴的直线上的点的纵坐标相同得出:B、C两点纵坐标相同,都是﹣2,过A点作AD⊥BC,垂足为D,根据垂直于x轴的直线上的点的横坐标相同及平行于x轴的直线上的点的纵坐标相同得出D点的坐标,根据等腰三角形的对称性得出CD=BD,进而得出BC的长,从而得出C点的坐标。
9.【答案】(1,1)
【解析】【解答】解:∵将点A′(-2,3)向右平移3个单位长度,
∴得到(1,3),
∵再向下平移2个单位长度,
∴平移后对应的点A′的坐标是:(1,1).
故答案为:(1,1).
【分析】根据点的平移规律:左减右加(横坐标减或加),上加下减(纵坐标加 或减),就可求出平移后对应的点A′的坐标。
10.【答案】2
【解析】【解答】解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,
由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,
所以点A. B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2. 故答案为:2
【分析】直接利用平移中点的变化规律求解即可.
11.【答案】解:(1)画出图形直接得到AB∥x轴,DC∥x轴,所以AB∥CD;(2)S=4×3=12
【解析】【分析】先在平面直角坐标系中描点、连线,画出图形。然后证明这是一个平行四边形,从而求出平行四边形ABCD的面积=底×高。
12.【答案】解:点在第一象限,点到轴和轴的距离相等,
,
解得:,
故,,
则点的坐标为:.
【解析】【分析】根据第一象限的点横坐标与纵坐标都是正数及一个点到x轴的距离等于其纵坐标的绝对值,到y轴的距离等于其横坐标的绝对值,可得2a-3=4+a,求出a的值,然后求出2a-3、4+a的值,据此可得点A的坐标.
13.【答案】解:(1)A→C(+3,+4),B→C(+2,0),C→D(+1,﹣2);
(2)1+4+2+1+2=10;
(3)点P如图所示.
【解析】【分析】(1)根据第一个数表示左右方向,第二个数表示上下方向结合图形写出即可;
(2)根据行走路线列出算式计算即可得解;
(3)根据方格和标记方法作出线路图即可得解.
14.【答案】解:由图象知:A(﹣2,0),D(2,7),E(2,3.5),
把△ABC向右平移2个单位长度,向上平移3.5个单位长度得到△CED.
【解析】【分析】根据网格结构和平移的性质即可得到结论.
课后提升答案:
1.【答案】C
【解析】【解答】解:由点(-1,-3)向上平移4个单位,再向左平移3个单位后的点的坐标为 .
故答案为:C.
【分析】根据平移的点的坐标变化特征“左减右加、上加下减”可求解.
2.【答案】B
【解析】【分析】根据平移时,点的坐标变化规律“上加下减,左减右加”进行计算.
【解答】根据题意,从点P到点P′,点P′的纵坐标不变,横坐标是-2+1=-1,
故点P′的坐标是(-1,1).
故选B.
3.【答案】C
【解析】【解答】解:∵点A(﹣3,﹣5)向左平移3个单位,再向上平移4个单位到点B,
∴点B的坐标为(﹣3﹣3,﹣5+4),即(﹣6,﹣1).
故选C.
【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
4.【答案】B
【解析】【解答】解:建立平面直角坐标系如图所示,
天安门(0,5),人民大会堂(﹣4,1),毛主席纪念堂(0,﹣3),正阳门(0,﹣5.5),
所以,建筑的点的坐标正确的是人民大会堂.
故选B.
【分析】以中国国家博物馆的位置向左4个单位,向下1个单位为坐标原点建立平面直角坐标系,然后写出各建筑点的坐标,从而得解.
5.【答案】B
【解析】【解答】解:平移后的横坐标为﹣2+3=1,
纵坐标为3,
∴点P(﹣2,3)向右平移3个单位长度后的坐标为(1,3),
故答案为:B.
【分析】让横坐标加3,纵坐标不变即可得到所求的坐标.
6.【答案】(5,2)
【解析】【解答】解:点 先向右平移2个单位,再向上平移3个单位,所得点的坐标为(5,2)
故答案为:(5,2).
【分析】根据坐标的平移特点“左减右加,上加下减”即可求解.
7.【答案】坐标;位置
【解析】【解答】有了平面直角坐标系,平面内的点可以用坐标来表示;同样一个点的坐标确定了该点在坐标平面内的位置.
故答案为:坐标;位置.
【分析】在平面直角坐标系中,要用两个数据才能表示一个点的位置,据此填空即可.
8.【答案】(4,1)或(0,1)
【解析】【解答】解:∵AB∥x轴,点A坐标为(2,1),
∴A,B的纵坐标相等为1,
设点B的横坐标为x,则有AB=|x 2|=2,
解得:x=4或0,
∴点B的坐标为(4,1)或(0,1),
故答案为:(4,1)或(0,1).
【分析】AB∥x轴,说明A,B的纵坐标相等为1,再根据两点之间的距离公式求解即可.
9.【答案】(-3,-6);(-4,-1)
【解析】【解答】根据题意可知使点A到点A′ ,所以△ABC是先向左平移2个单位长度,再向下平移4个单位长度,所以点B,C的横坐标分别减2,纵坐标分别减4,即点B、C平移后对应点的坐标分别为(-3,-6),(-4,-1).
【分析】本题先根据点A的平移确定平移方式,再求出点B,C平移后对应点的坐标.
10.【答案】四
【解析】【解答】解:点P(3,-4)在第四象限.
11.【答案】(1)(-2,3);(-6,0);(-1,0)
(2)解:如图所示:
(3)关于x轴对称
【解析】【解答】(1)A点的坐标为(-2,3);B点的坐标为(-6,0);C点的坐标为(-1,0).(3)关于x轴对称.
【分析】(1)由平面直角坐标系的图象可以写出A、B、C坐标;
(2)先由ΔABC的纵坐标乘以-1,然后在平面直角坐标系中描出各点即可画出ΔA'B'C';
(3)由图象可以看出,两个三角形关于x轴对称。
12.【答案】解:由图中坐标系可知各点的坐标为:A(﹣2,0),B(2,0),C(1,2),D(0,4),E(﹣1,2),F(0,2),
O(0,0).
【解析】【分析】直接根据图示,在网格中数出对应的点的坐标即可.
13.【答案】解:∵A(2,4),B(7,2),
∴AC=2、CO=4、OE=7、BE=2、AF=4、EF=OE﹣OF=7﹣2=5,
由图可知,S△AOB=S矩形ACOF+S梯形AFEB﹣S△ACO﹣S△BOE,
=2×4+(2+4)×5﹣×2×4﹣×7×2,
=8+15﹣4﹣7,
=23﹣11,
=12.
【解析】【分析】根据点A、B的坐标求出AC、CO、OE、BE、AF、EF的长度,然后根据S△AOB=S矩形ACOF+S梯形AFEB﹣S△ACO﹣S△BOE列式计算即可得解.
14.【答案】解:(1)一1表示我,三2表示是,二4表示最,四3表示棒,五1表示的,所以礼物为:我是最棒的;(2)五3表示努,二1表示力,二3表示就,一5表示能,三4行,所以礼物为:努力就能行;(3)四5表示明,四1表示天,一2表示会,三3表示更,五2表示好,所以礼物为:明天会更好.
【解析】【分析】(1)根据表格,分别找出一1→三2→二4→四3→五1表示的汉字,排列即可;
(2)根据表格,分别找出五3→二1→二3→一5→三4表示的汉字,排列即可;
(3)根据表格,分别找出四5→四1→一2→三3→五2表示的汉字,排列即可.
