2022-2023学年人教版八年级数学下册18.1.1平行四边形的性质同步练习 (含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册18.1.1平行四边形的性质同步练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 143.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-11 22:47:38 | ||
图片预览


文档简介
2023年八年级下册 数学第十八章【同步测试】+【课后提升】
18.1.1平行四边形的性质
同步测试阶段:
一、单选题
1.如图, ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是( )
A.10 B.8 C.7 D.6
2.在平行四边形ABCD中,∠D、∠C的度数之比为3∶1,则∠A等于( )
A.45° B.135° C.50° D.130°
3.如图,在 ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=3,则四边形ABCD的面积为( )
A.6 B.12 C.20 D.24
4.已知□ABCD的周长是26cm,其中△ABC的周长是18cm,则AC的长为( )
A.12cm B.10cm C.8cm D.5cm
5.平行线之间的距离是指( )
A.从一条直线上一点到另一直线的垂线段
B.从一条直线上一点到另一条直线的垂线段长度
C.从一条直线上一点到另一条直线的垂线的长度
D.从一条直线上一点到另一条直线上的一点间线段的长度
二、填空题
6.若□ABCD中,∠A=50°,则∠C=° .
7.如图所示,在平行四边形ABCD中,DE平分∠ADC交BC于E,AF⊥DE,垂足为F,已知∠DAF=50°,则∠C的度数是 .
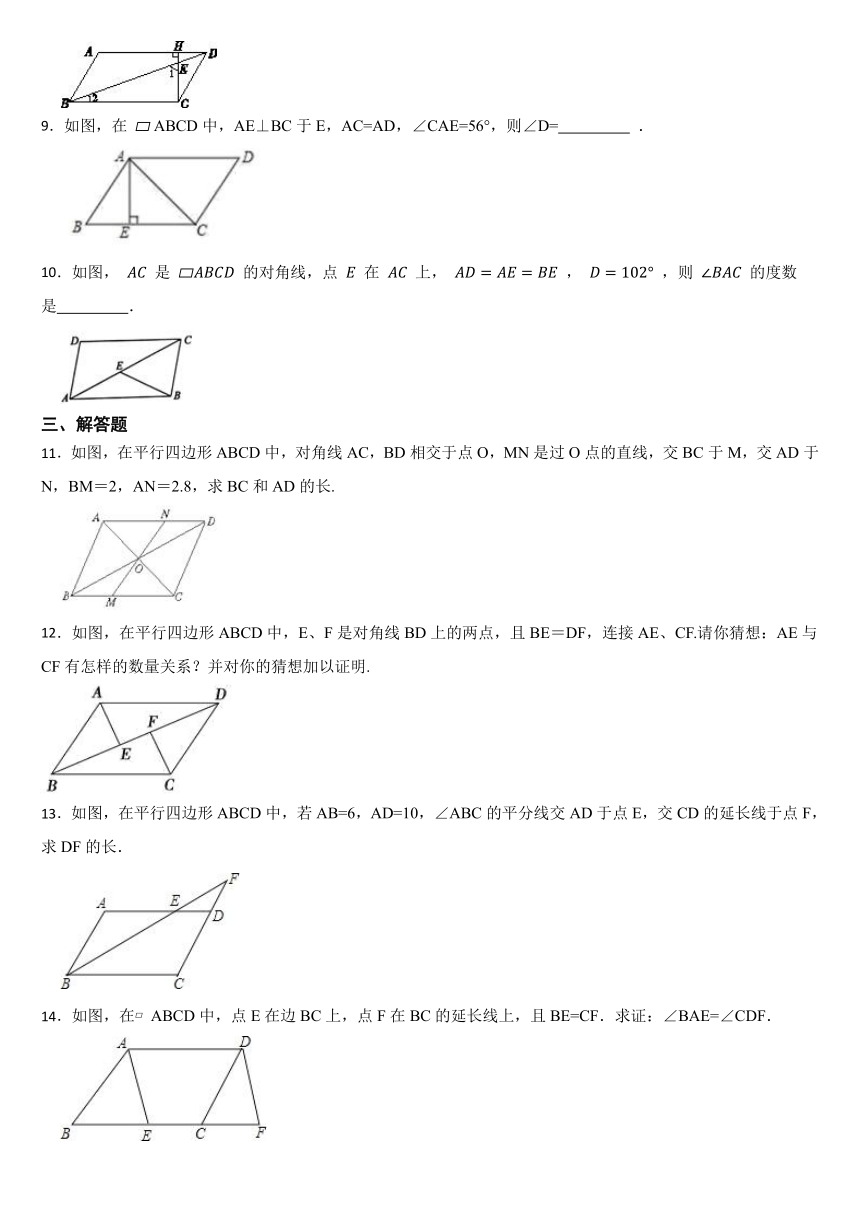
8.如图,在 ABCD中,CH⊥AD于点H,CH与BD的交点为E.如果 , ,那么
9.如图,在 ABCD中,AE⊥BC于E,AC=AD,∠CAE=56°,则∠D= .
10.如图, 是 的对角线,点 在 上, , ,则 的度数是 .
三、解答题
11.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,MN是过O点的直线,交BC于M,交AD于N,BM=2,AN=2.8,求BC和AD的长.
12.如图,在平行四边形ABCD中,E、F是对角线BD上的两点,且BE=DF,连接AE、CF.请你猜想:AE与CF有怎样的数量关系?并对你的猜想加以证明.
13.如图,在平行四边形ABCD中,若AB=6,AD=10,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
14.如图,在 ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.求证:∠BAE=∠CDF.
课后提升阶段:
一、单选题
1.如图,在平行四边形ABCD中,∠ODA=90°,AC=10,BD=6,则AD的长为( )
A.4 B.5 C.6 D.8
2.在下列性质中,平行四边形不一定具有的是( )
A.对边相等 B.对角互补 C.对边平行 D.对角相等
3.如图,在平行四边形ABCD中,若∠A=40°,则∠D的度数为( )
A.40° B.100° C.140° D.180°
4.如图,直线 ,点P是直线 上一个动点,当点P的位置发生变化时,三角形 的面积( )
A.向左移动变小 B.向右移动变小
C.始终不变 D.无法确定
5.在 ABCD中,∠ABC的角平分线交线段AD于点E,DE=1,点F是BE中点,连接CF,过点F作FG⊥BC,垂足为G,设AB=x,若 ABCD的面积为8,FG的长为整数,则整数x的值为( )
A.1 B.2 C.3 D.2或3
二、填空题
6.在 ABCD中,AB=4cm,BC=6cm,则 ABCD的周长为 cm
7. 中, , ,则 的周长为 .
8.如图,在平行四边形ABCD中,∠B<90°,BC>AB,点E、F分别在边BC和CD上,AE=6,AF=8,∠EAF=60°.
(1)若AE⊥BC,AF⊥CD,则CD:BC= ;
(2)若点E、F在分别是边BC和CD的中点,则AD= .
9.如图,E是ABCD边BC上的一点,且AB=BE,连结AE,并延长AE与DC的延长线交于点F,∠F=60°,则∠D= .
10.在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下列结论:
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
其中正确的有 .(填序号)
三、解答题
11.如图,在 ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE=CF.
12.已知的边长如图所示,求的周长.
13.如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.
14.已知:E、F是 ABCD的对角线AC上的两点,AF=CE,求证:∠CDF=∠ABE.
同步测试答案:
1.【答案】D
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴OA=AC=3,OB=BD=4,
在△AOB中:4﹣3<AB<4+3,
即1<AB<7,
∴AB的长可能为6.
故答案为:D.
【分析】根据平行四边形的性质可得OA=AC=3,OB=BD=4,再利用三角形三边的关系求解即可。
2.【答案】A
【解析】【解答】如图所示,
∵在 ABCD中,∠D、∠C的度数之比为3:1,
∴∠B:∠A=3:1,
则3∠A+∠A=180°,
解得:∠A=45°.
故答案为:A.
【分析】根据平行四边形的对角相等,可得∠B:∠A=∠D:∠C=3:1,根据平行四边形的邻角互补,可得∠B+∠A=180°,据此解答即可.
3.【答案】D
【解析】【解答】∵四边形ABCD 是平行四边形,
∴BD=2BE=6,
∵∠CBD=90°,
∴四边形ABCD的面积为:BC BD=4×6=24.
故答案为:D.
【分析】根据平行四边形的性质,可得BD的长,根据平行四边形的面积公式,可得答案.
4.【答案】D
【解析】【解答】∵□ABCD的周长是26cm,∴AB+BC=26÷2=13cm.
∵△ABC的周长是18cm,∴AC=18-13=5cm
故答案为:D.
【分析】根据平行四边形的性质,对边相等,由□ABCD的周长,得到AB+BC的值,由△ABC的周长,求出AC的值.
5.【答案】B
【解析】【解答】解:平行线之间的距离是指:从一条直线上一点到另一条直线的垂线段长度.
故选B.
【分析】根据平行线间的距离的定义直接进行选择即可.
6.【答案】50
【解析】【解答】因为平行四边形的对角相等,所以∠C=50°,
故答案为:50°.
【分析】根据平行四边形对角相等的性质可知∠C=∠A.
7.【答案】100°
【解析】【解答】解:∵AF⊥DE,
∴∠AFD=90°,
∵∠DAF=50°,
∴∠ADF=90°﹣50°=40°,
∵DE平分∠ADC,
∴∠ADC=2∠ADF=80°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠ADC=180°,
∴∠C=100°
故答案为100°
【分析】根据三角形的内角和得出∠ADF的度数,根据角平分线的定义得出∠ADC=2∠ADF=80°,根据平行四边形的对边平行得出AD∥BC,根据二直线平行同旁内角互补得出∠C+∠ADC=180°,从而即可算出答案。
8.【答案】60°
【解析】【解答】解:∵∠1=70°,∴∠DEH=70°.
∵CH⊥AD, ∴∠HDE=90°-70°=20°.
∵AD∥BC, ∴∠2=∠HDE==20°.
∵∠ABC=3∠2,∴∠ABC=60°.
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC=60°.
9.【答案】73°
【解析】【解答】解:∵AE⊥BC于E,
∴∠AEC=90°,
∵∠CAE=56°,
∴∠ACE=34°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACE=34°,
∴∠D+∠ACD=146°,
∵AC=AD,
∴∠D=∠ACD=73°,
根据答案为:73°.
【分析】先求出∠ACE=34°,再根据平行四边形的性质和平行线的性质得出∠DAC=∠ACE=34°,从而得出∠D+∠ACD=146°,再根据等腰三角形的性质得出∠D=∠ACD=73°,即可得出答案.
10.【答案】26
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AD=BC, ∠ABC=∠D=102°,
∵AD=AE=BE,
∴BC=AE=BE,
∴∠EAB=∠EBA,∠BEC=∠BCA,
∵∠BEC=∠EAB+∠EBA=2∠EAB,
∴∠ACB=2∠BAC,
∴∠BAC+∠ACB=3∠BAC=180°-∠ABC=180°-102°=78°,
∴3∠BAC=78°,
即∠BAC=26°,
故答案为:26°.
【分析】根据平行四边形及等腰三角形的性质可得∠EAB=∠EBA,∠BEC=∠BCA,再利用三角形外角的性质可得∠ACB=2∠BAC,然后由三角形内角和定理求解即可。
11.【答案】解:在平行四边新ABCD中,
∵对角线AC,BD相交于点O,MN是过O点的直线,
∴AN=MC DN=BM
∵BC=BM+MC
∴BC=BM+AN=2+2.8=4.8
∵AD=BC
∴AD=4.8
【解析】【分析】根据平行四边形的性质可求得BC和AD的长。
12.【答案】解: 猜想:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS),
∴AE=CF.
【解析】【分析】考查平行四边形的性质。
13.【答案】解:∵四边形ABCD为平行四边形,
∴AB=DC=6,AD=BC=10,AB∥DC.
∵AB∥DC,
∴∠1=∠3,
又∵BF平分∠ABC,
∴∠1=∠2,
∴∠2=∠3,
∴BC=CF=10,
∴DF=CF﹣DC=10﹣6=4
【解析】【分析】首先根据平行四边形的性质可得AB=DC=6,AD=BC=10,AB∥DC,再根据平行线的性质与角平分线的性质证明∠2=∠3,根据等角对等边可得BC=CF=10,再用CF﹣CD即可算出DF的长.
14.【答案】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠B=∠DCF,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠BAE=∠CDF
【解析】【分析】首先根据平行四边形的性质可得AB=CD,AB∥CD,再根据平行线的性质可得∠B=∠DCF,即可证明△ABE≌△DCF,再根据全等三角形性质可得到结论.
课后提升答案:
1.【答案】A
【解析】【解答】解:∵四边形ABCD是平行四边形,AC=10,BD=6,
∴OA=OC=AC=5,OB=OD=BD=3,
∵∠ODA=90°,
∴在Rt△ADO中,由勾股定理可知,,
故答案为:A.
【分析】根据平行四边形的性质可得OA=OC=AC=5,OB=OD=BD=3,再利用勾股定理可得。
2.【答案】B
【解析】【解答】解:∵平行四边形的对边平行、对角相等、对边相等,
∴选项B不符合题意;
故答案为B.
【分析】根据平行四边形的性质逐项排除即可
3.【答案】C
【解析】【解答】∵平行四边形ABCD
∴
∴
∵∠A=40°
∴
故答案为:C.
【分析】利用平行四边形的性质:邻角互补,对角相等求解即可。
4.【答案】C
【解析】【解答】解:∵直线 ,点P是直线 AB 上一个动点,
∴无论点P怎么移动,点P到CD的距离不变,
∴三角形PCD 的底不变,高不变,面积也不变,
故答案为:C.
【分析】根据平行线间的距离处处相等,可知三角形 PCD 的底不变,高相等,从而得出面积始终不变.
5.【答案】C
【解析】【解答】解:延长GF交AD于点H,如图所示.
∵四边形ABCD是平行四边形,FG⊥BC,
∴∠FHE=∠FGB=90°,AD∥BC,
∴∠AEB=∠EBC.
∵点F为BE的中点,∴EF=BF,
又∵∠HFE=∠GFB,
∴△HFE≌△GFB(AAS),
∴HF=GF,
∴HG=2GF.
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE.
∵AB=x,∴AE=x.
∵DE=1,∴AD=x+1.
∵ ABCD的面积为8,FG的长为整数,∴(x+1) 2GF=8,∴整数x为1或3.
∵当x=1时,AB=1,AD=2,则此时平行四边形的面不可能是8,故舍去,∴x=3.
故答案为:C.
【分析】根据题意和平行四边形的性质,可以得到AD和AB的关系,然后根据 ABCD的面积为8,FG的长为整数,从而可以得到整数x的值.
6.【答案】20
【解析】【解答】解:在平行四边形ABCD中,
AB=4cm,BC=6cm,
则其周长为2(AB+BC)=2(4+6)=20cm.
所以其周长为20cm.
故答案为:20.
【分析】平行四边形的周长=(长+宽)×2,据此计算即可.
7.【答案】18
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD=5,AD=BC=4,
∴ ABCD的周长为:2×(AB+AD)=2×(5+4)=18,
故答案为:18.
【分析】由平行四边形性质得出AB=CD=5,AD=BC=4,即可得出结果.
8.【答案】(1)3:4
(2)
【解析】【解答】解:(1)连接AC,如图,
∵平行四边形ABCD,
∴S△ABC=S△ACD,
即 BC AE= CD AF,
∵AE=6,AF=8,
∴3BC=4AF,
∴CD:BC=3:4,
故答案为:3:4.
( 2 )延长AF与BC延长线交于点M,过点M作MN⊥AE交AE的延长线于点N,如图,
∵平行四边形ABCD,
∴AD=BC,AD∥BM,
∴∠ADF=∠MCF,
∵F为CD的中点,
∴CF=DF,
在△AFD和△MFC,
,
∴△AFD≌△MFC(ASA),
∴AD=CM,AF=FM,
∴AM=2AF=16,
∵∠EAF=60°,∠N=90°,
∴∠AMN=30°,
∴AN= AM=8,MN= =8 ,
∵AE=6,
∴EN=AN﹣AE=2,
∴EM= =14,
∵E为BC中点,
∴EC= = AD= ,
∴EM=EC+CM= CM= AD,
∴AD= EM= ,
故答案为:
【分析】(1)连接AC,由平行四边形的性质可得S△ABC=S△ACD,于是根据面积法可求解;
(2)延长AF与BC延长线交于点M,过点M作MN⊥AE交AE的延长线于点N,由平行四边形的性质可得AD=BC,AD∥BM,结合已知用角边角可证△AFD≌△MFC,由全等三角形的对应边相等得AD=CM,AF=FM,于是AM=2AF,用三角形内角和定理得∠AMN=30°,根据30度角的直角三角形的性质可得AN=AM,然后用勾股定理可求得MN、EM的值,由线段中点的定义得EC=BC=AD=CM,由线段的构成EM=EC+CM可求得EM的值,于是AD=EM可求解.
9.【答案】60°
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,∠B=∠D,
∴∠BAE=∠F=60°,
∵AB=BE,
∴△ABE是等边三角形,
∴∠B=60°,
∴∠D=60°,
故答案为:60°.
【分析】先证明△ABE是等边三角形,可得∠B=60°,再根据平行四边形的性质可得∠D=∠B=60°。
10.【答案】①②④
【解析】【解答】解:∵当 ABCD的面积最大时,AB⊥BC,
∴ ABCD是矩形,
∴∠A=∠C=90°,AC=BD,故③错误,④正确;
∴∠A+∠C=180°;故②正确;
∴AC= =5,故①正确.
故答案为:①②④.
【分析】由当 ABCD的面积最大时,AB⊥BC,可判定 ABCD是矩形,由矩形的性质,可得②④正确,③错误,又由勾股定理求得AC=5.
11.【答案】证明:如图,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF.
又BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
在△ABE与△CDF中,
,
∴得△ABE≌△CDF(AAS),
∴AE=CF.
【解析】【分析】根据平行四边形的对边平行且相等得出 AB=CD,AB∥CD, 根据二直线平行,内错角相等得出 ∠BAE=∠DCF,根据垂直的定义得出 ∠AEB=∠CFD=90°,从而利用AAS判断出 △ABE≌△CDF ,根据全等三角形对应边相等得出 AE=CF 。
12.【答案】解:四边形ABCD是平行四边形,
,
解方程得
经检验是原方程的根
∴的周长
【解析】【分析】根据平行四边形的性质可得,求出x的值,再求出AB和AD的长,最后利用平行四边形的周长公式计算即可。
13.【答案】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠E=∠BAE,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠E=∠DAE,
∴DA=DE
【解析】【分析】由平行四边形的性质得出AB∥CD,得出内错角相等∠E=∠BAE,再由角平分线证出∠E=∠DAE,即可得出结论.
14.【答案】证明:∵AF=CE.
∴AE=CF,
∵在 ABCD中,AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中, ,
∴△ABE≌△CDF(SAS),
∴∠CDF=∠ABE.
【解析】【分析】根据平行四边形的对边相等可得AB=CD,对边平行可得AB∥CD,再根据两直线平行,内错角相等可得∠BAE=∠DCF,然后利用“边角边”证明△ABE和△CDF全等,根据全等三角形对应边相等可得结论.
18.1.1平行四边形的性质
同步测试阶段:
一、单选题
1.如图, ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是( )
A.10 B.8 C.7 D.6
2.在平行四边形ABCD中,∠D、∠C的度数之比为3∶1,则∠A等于( )
A.45° B.135° C.50° D.130°
3.如图,在 ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=3,则四边形ABCD的面积为( )
A.6 B.12 C.20 D.24
4.已知□ABCD的周长是26cm,其中△ABC的周长是18cm,则AC的长为( )
A.12cm B.10cm C.8cm D.5cm
5.平行线之间的距离是指( )
A.从一条直线上一点到另一直线的垂线段
B.从一条直线上一点到另一条直线的垂线段长度
C.从一条直线上一点到另一条直线的垂线的长度
D.从一条直线上一点到另一条直线上的一点间线段的长度
二、填空题
6.若□ABCD中,∠A=50°,则∠C=° .
7.如图所示,在平行四边形ABCD中,DE平分∠ADC交BC于E,AF⊥DE,垂足为F,已知∠DAF=50°,则∠C的度数是 .
8.如图,在 ABCD中,CH⊥AD于点H,CH与BD的交点为E.如果 , ,那么
9.如图,在 ABCD中,AE⊥BC于E,AC=AD,∠CAE=56°,则∠D= .
10.如图, 是 的对角线,点 在 上, , ,则 的度数是 .
三、解答题
11.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,MN是过O点的直线,交BC于M,交AD于N,BM=2,AN=2.8,求BC和AD的长.
12.如图,在平行四边形ABCD中,E、F是对角线BD上的两点,且BE=DF,连接AE、CF.请你猜想:AE与CF有怎样的数量关系?并对你的猜想加以证明.
13.如图,在平行四边形ABCD中,若AB=6,AD=10,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
14.如图,在 ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.求证:∠BAE=∠CDF.
课后提升阶段:
一、单选题
1.如图,在平行四边形ABCD中,∠ODA=90°,AC=10,BD=6,则AD的长为( )
A.4 B.5 C.6 D.8
2.在下列性质中,平行四边形不一定具有的是( )
A.对边相等 B.对角互补 C.对边平行 D.对角相等
3.如图,在平行四边形ABCD中,若∠A=40°,则∠D的度数为( )
A.40° B.100° C.140° D.180°
4.如图,直线 ,点P是直线 上一个动点,当点P的位置发生变化时,三角形 的面积( )
A.向左移动变小 B.向右移动变小
C.始终不变 D.无法确定
5.在 ABCD中,∠ABC的角平分线交线段AD于点E,DE=1,点F是BE中点,连接CF,过点F作FG⊥BC,垂足为G,设AB=x,若 ABCD的面积为8,FG的长为整数,则整数x的值为( )
A.1 B.2 C.3 D.2或3
二、填空题
6.在 ABCD中,AB=4cm,BC=6cm,则 ABCD的周长为 cm
7. 中, , ,则 的周长为 .
8.如图,在平行四边形ABCD中,∠B<90°,BC>AB,点E、F分别在边BC和CD上,AE=6,AF=8,∠EAF=60°.
(1)若AE⊥BC,AF⊥CD,则CD:BC= ;
(2)若点E、F在分别是边BC和CD的中点,则AD= .
9.如图,E是ABCD边BC上的一点,且AB=BE,连结AE,并延长AE与DC的延长线交于点F,∠F=60°,则∠D= .
10.在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下列结论:
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
其中正确的有 .(填序号)
三、解答题
11.如图,在 ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE=CF.
12.已知的边长如图所示,求的周长.
13.如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.
14.已知:E、F是 ABCD的对角线AC上的两点,AF=CE,求证:∠CDF=∠ABE.
同步测试答案:
1.【答案】D
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴OA=AC=3,OB=BD=4,
在△AOB中:4﹣3<AB<4+3,
即1<AB<7,
∴AB的长可能为6.
故答案为:D.
【分析】根据平行四边形的性质可得OA=AC=3,OB=BD=4,再利用三角形三边的关系求解即可。
2.【答案】A
【解析】【解答】如图所示,
∵在 ABCD中,∠D、∠C的度数之比为3:1,
∴∠B:∠A=3:1,
则3∠A+∠A=180°,
解得:∠A=45°.
故答案为:A.
【分析】根据平行四边形的对角相等,可得∠B:∠A=∠D:∠C=3:1,根据平行四边形的邻角互补,可得∠B+∠A=180°,据此解答即可.
3.【答案】D
【解析】【解答】∵四边形ABCD 是平行四边形,
∴BD=2BE=6,
∵∠CBD=90°,
∴四边形ABCD的面积为:BC BD=4×6=24.
故答案为:D.
【分析】根据平行四边形的性质,可得BD的长,根据平行四边形的面积公式,可得答案.
4.【答案】D
【解析】【解答】∵□ABCD的周长是26cm,∴AB+BC=26÷2=13cm.
∵△ABC的周长是18cm,∴AC=18-13=5cm
故答案为:D.
【分析】根据平行四边形的性质,对边相等,由□ABCD的周长,得到AB+BC的值,由△ABC的周长,求出AC的值.
5.【答案】B
【解析】【解答】解:平行线之间的距离是指:从一条直线上一点到另一条直线的垂线段长度.
故选B.
【分析】根据平行线间的距离的定义直接进行选择即可.
6.【答案】50
【解析】【解答】因为平行四边形的对角相等,所以∠C=50°,
故答案为:50°.
【分析】根据平行四边形对角相等的性质可知∠C=∠A.
7.【答案】100°
【解析】【解答】解:∵AF⊥DE,
∴∠AFD=90°,
∵∠DAF=50°,
∴∠ADF=90°﹣50°=40°,
∵DE平分∠ADC,
∴∠ADC=2∠ADF=80°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠ADC=180°,
∴∠C=100°
故答案为100°
【分析】根据三角形的内角和得出∠ADF的度数,根据角平分线的定义得出∠ADC=2∠ADF=80°,根据平行四边形的对边平行得出AD∥BC,根据二直线平行同旁内角互补得出∠C+∠ADC=180°,从而即可算出答案。
8.【答案】60°
【解析】【解答】解:∵∠1=70°,∴∠DEH=70°.
∵CH⊥AD, ∴∠HDE=90°-70°=20°.
∵AD∥BC, ∴∠2=∠HDE==20°.
∵∠ABC=3∠2,∴∠ABC=60°.
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC=60°.
9.【答案】73°
【解析】【解答】解:∵AE⊥BC于E,
∴∠AEC=90°,
∵∠CAE=56°,
∴∠ACE=34°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACE=34°,
∴∠D+∠ACD=146°,
∵AC=AD,
∴∠D=∠ACD=73°,
根据答案为:73°.
【分析】先求出∠ACE=34°,再根据平行四边形的性质和平行线的性质得出∠DAC=∠ACE=34°,从而得出∠D+∠ACD=146°,再根据等腰三角形的性质得出∠D=∠ACD=73°,即可得出答案.
10.【答案】26
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AD=BC, ∠ABC=∠D=102°,
∵AD=AE=BE,
∴BC=AE=BE,
∴∠EAB=∠EBA,∠BEC=∠BCA,
∵∠BEC=∠EAB+∠EBA=2∠EAB,
∴∠ACB=2∠BAC,
∴∠BAC+∠ACB=3∠BAC=180°-∠ABC=180°-102°=78°,
∴3∠BAC=78°,
即∠BAC=26°,
故答案为:26°.
【分析】根据平行四边形及等腰三角形的性质可得∠EAB=∠EBA,∠BEC=∠BCA,再利用三角形外角的性质可得∠ACB=2∠BAC,然后由三角形内角和定理求解即可。
11.【答案】解:在平行四边新ABCD中,
∵对角线AC,BD相交于点O,MN是过O点的直线,
∴AN=MC DN=BM
∵BC=BM+MC
∴BC=BM+AN=2+2.8=4.8
∵AD=BC
∴AD=4.8
【解析】【分析】根据平行四边形的性质可求得BC和AD的长。
12.【答案】解: 猜想:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS),
∴AE=CF.
【解析】【分析】考查平行四边形的性质。
13.【答案】解:∵四边形ABCD为平行四边形,
∴AB=DC=6,AD=BC=10,AB∥DC.
∵AB∥DC,
∴∠1=∠3,
又∵BF平分∠ABC,
∴∠1=∠2,
∴∠2=∠3,
∴BC=CF=10,
∴DF=CF﹣DC=10﹣6=4
【解析】【分析】首先根据平行四边形的性质可得AB=DC=6,AD=BC=10,AB∥DC,再根据平行线的性质与角平分线的性质证明∠2=∠3,根据等角对等边可得BC=CF=10,再用CF﹣CD即可算出DF的长.
14.【答案】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠B=∠DCF,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠BAE=∠CDF
【解析】【分析】首先根据平行四边形的性质可得AB=CD,AB∥CD,再根据平行线的性质可得∠B=∠DCF,即可证明△ABE≌△DCF,再根据全等三角形性质可得到结论.
课后提升答案:
1.【答案】A
【解析】【解答】解:∵四边形ABCD是平行四边形,AC=10,BD=6,
∴OA=OC=AC=5,OB=OD=BD=3,
∵∠ODA=90°,
∴在Rt△ADO中,由勾股定理可知,,
故答案为:A.
【分析】根据平行四边形的性质可得OA=OC=AC=5,OB=OD=BD=3,再利用勾股定理可得。
2.【答案】B
【解析】【解答】解:∵平行四边形的对边平行、对角相等、对边相等,
∴选项B不符合题意;
故答案为B.
【分析】根据平行四边形的性质逐项排除即可
3.【答案】C
【解析】【解答】∵平行四边形ABCD
∴
∴
∵∠A=40°
∴
故答案为:C.
【分析】利用平行四边形的性质:邻角互补,对角相等求解即可。
4.【答案】C
【解析】【解答】解:∵直线 ,点P是直线 AB 上一个动点,
∴无论点P怎么移动,点P到CD的距离不变,
∴三角形PCD 的底不变,高不变,面积也不变,
故答案为:C.
【分析】根据平行线间的距离处处相等,可知三角形 PCD 的底不变,高相等,从而得出面积始终不变.
5.【答案】C
【解析】【解答】解:延长GF交AD于点H,如图所示.
∵四边形ABCD是平行四边形,FG⊥BC,
∴∠FHE=∠FGB=90°,AD∥BC,
∴∠AEB=∠EBC.
∵点F为BE的中点,∴EF=BF,
又∵∠HFE=∠GFB,
∴△HFE≌△GFB(AAS),
∴HF=GF,
∴HG=2GF.
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE.
∵AB=x,∴AE=x.
∵DE=1,∴AD=x+1.
∵ ABCD的面积为8,FG的长为整数,∴(x+1) 2GF=8,∴整数x为1或3.
∵当x=1时,AB=1,AD=2,则此时平行四边形的面不可能是8,故舍去,∴x=3.
故答案为:C.
【分析】根据题意和平行四边形的性质,可以得到AD和AB的关系,然后根据 ABCD的面积为8,FG的长为整数,从而可以得到整数x的值.
6.【答案】20
【解析】【解答】解:在平行四边形ABCD中,
AB=4cm,BC=6cm,
则其周长为2(AB+BC)=2(4+6)=20cm.
所以其周长为20cm.
故答案为:20.
【分析】平行四边形的周长=(长+宽)×2,据此计算即可.
7.【答案】18
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD=5,AD=BC=4,
∴ ABCD的周长为:2×(AB+AD)=2×(5+4)=18,
故答案为:18.
【分析】由平行四边形性质得出AB=CD=5,AD=BC=4,即可得出结果.
8.【答案】(1)3:4
(2)
【解析】【解答】解:(1)连接AC,如图,
∵平行四边形ABCD,
∴S△ABC=S△ACD,
即 BC AE= CD AF,
∵AE=6,AF=8,
∴3BC=4AF,
∴CD:BC=3:4,
故答案为:3:4.
( 2 )延长AF与BC延长线交于点M,过点M作MN⊥AE交AE的延长线于点N,如图,
∵平行四边形ABCD,
∴AD=BC,AD∥BM,
∴∠ADF=∠MCF,
∵F为CD的中点,
∴CF=DF,
在△AFD和△MFC,
,
∴△AFD≌△MFC(ASA),
∴AD=CM,AF=FM,
∴AM=2AF=16,
∵∠EAF=60°,∠N=90°,
∴∠AMN=30°,
∴AN= AM=8,MN= =8 ,
∵AE=6,
∴EN=AN﹣AE=2,
∴EM= =14,
∵E为BC中点,
∴EC= = AD= ,
∴EM=EC+CM= CM= AD,
∴AD= EM= ,
故答案为:
【分析】(1)连接AC,由平行四边形的性质可得S△ABC=S△ACD,于是根据面积法可求解;
(2)延长AF与BC延长线交于点M,过点M作MN⊥AE交AE的延长线于点N,由平行四边形的性质可得AD=BC,AD∥BM,结合已知用角边角可证△AFD≌△MFC,由全等三角形的对应边相等得AD=CM,AF=FM,于是AM=2AF,用三角形内角和定理得∠AMN=30°,根据30度角的直角三角形的性质可得AN=AM,然后用勾股定理可求得MN、EM的值,由线段中点的定义得EC=BC=AD=CM,由线段的构成EM=EC+CM可求得EM的值,于是AD=EM可求解.
9.【答案】60°
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,∠B=∠D,
∴∠BAE=∠F=60°,
∵AB=BE,
∴△ABE是等边三角形,
∴∠B=60°,
∴∠D=60°,
故答案为:60°.
【分析】先证明△ABE是等边三角形,可得∠B=60°,再根据平行四边形的性质可得∠D=∠B=60°。
10.【答案】①②④
【解析】【解答】解:∵当 ABCD的面积最大时,AB⊥BC,
∴ ABCD是矩形,
∴∠A=∠C=90°,AC=BD,故③错误,④正确;
∴∠A+∠C=180°;故②正确;
∴AC= =5,故①正确.
故答案为:①②④.
【分析】由当 ABCD的面积最大时,AB⊥BC,可判定 ABCD是矩形,由矩形的性质,可得②④正确,③错误,又由勾股定理求得AC=5.
11.【答案】证明:如图,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF.
又BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
在△ABE与△CDF中,
,
∴得△ABE≌△CDF(AAS),
∴AE=CF.
【解析】【分析】根据平行四边形的对边平行且相等得出 AB=CD,AB∥CD, 根据二直线平行,内错角相等得出 ∠BAE=∠DCF,根据垂直的定义得出 ∠AEB=∠CFD=90°,从而利用AAS判断出 △ABE≌△CDF ,根据全等三角形对应边相等得出 AE=CF 。
12.【答案】解:四边形ABCD是平行四边形,
,
解方程得
经检验是原方程的根
∴的周长
【解析】【分析】根据平行四边形的性质可得,求出x的值,再求出AB和AD的长,最后利用平行四边形的周长公式计算即可。
13.【答案】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠E=∠BAE,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠E=∠DAE,
∴DA=DE
【解析】【分析】由平行四边形的性质得出AB∥CD,得出内错角相等∠E=∠BAE,再由角平分线证出∠E=∠DAE,即可得出结论.
14.【答案】证明:∵AF=CE.
∴AE=CF,
∵在 ABCD中,AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中, ,
∴△ABE≌△CDF(SAS),
∴∠CDF=∠ABE.
【解析】【分析】根据平行四边形的对边相等可得AB=CD,对边平行可得AB∥CD,再根据两直线平行,内错角相等可得∠BAE=∠DCF,然后利用“边角边”证明△ABE和△CDF全等,根据全等三角形对应边相等可得结论.
