《名师学典·数学》人教版八年级下册第十七章 勾股定理 本章复习学案
文档属性
| 名称 | 《名师学典·数学》人教版八年级下册第十七章 勾股定理 本章复习学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 436.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-15 00:00:00 | ||
图片预览


文档简介
jj《名题学典·数学》人教版八年级系列第十七章
第5课时 本章复习
1. 直角三角形的定义、性质:有一角为直角的三角形为直角三角形,其中两个锐角互余.
2.直角三角有关的定理:
(1)直角三角形中,如果一个角为30°,那么它所对的直角边是斜边的一半;
(2)勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么.
(3)勾股定理的逆定理:如果三角形的三边长a,b,c满足,那么这个三角形是直角三角形.(判定直角三角形)
3.等腰直角三角形:等腰直角三角形是特殊的等腰三角形,除了有等腰三角形的性质外,它的顶角为直角,两个锐角都是45°,且其斜边长是直角边长的倍.
4.勾股定理的证明:赵爽弦图(课本23页).21世纪教育网版权所有
5.勾股定理的应用:(1)直角根据勾股定理求直角边或斜边;(2)解决方位类型题;(3)根据定长的位置变化求它的值:如梯子的长,旗杆的长等问题;(3)最短路径:立体展开,求最短路径、平面两点间的最短路径等问题.21世纪教育网版权所有
6.勾股定理的逆定理的应用:判断直角三角形.21世纪教育网版权所有
7.这一章所学的其他概念:
(1)互逆命题:如果两个命题的题设、结论正好相反,那么这两个命题叫做互逆命题;如果把其中一个叫原命题,那么另外一个就是逆命题;
(2)互逆定理:一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理为互逆定理;如勾股定理、勾股定理的逆定理;
(3)勾股数:像15,8,17这样,能够成为直角三角形三条连长的三个正整数,称为勾股数.
8.作图:(1)会画赵爽弦图;(2)会在数轴上表示出带根号的数,如,等.
考点1:逆命题和逆定理
【例1】在下列定理中,没有逆定理的是( )
A.有斜边和一直角边对应相等的两个直角三角形全等
B.直角三角形两个锐角互余
C.全等三角形对应角相等
D.角平分线上的点到这个角两边的距离相等
分析:首先要区分逆命题和逆定理,逆命题是与原命题(成立或不成立)的题设、结论相反的,成立或者不成立;如果某定理的逆命题是成立的,那么该逆命题就是原定理的逆定理;如果该定理的逆命题不成立,那么它就没有逆定理.先写出各选项的逆命题,判断出其真假即可解答.
解:C
解析:A. 其逆命题是“两个直角三角形全等,那么斜边和一直角边对应相等”,正确,所以有逆定理;
B. 其逆命题是“两个锐角互余的三角形是直角三角形”,正确,所以有逆定理;
C. 其逆命题是“对应角相等的三角形是全等三角形”,错误,所以没有逆定理;
D. 其逆命题是“到角两边距离相等的点在角的平分线上”,正确,所以有逆定理.
练习1
(1)请写出定理:“等腰三角形的两个底角相等”的逆定理 .
(2)已知命题“等腰三角形两腰上的高相等”.
①写出逆命题;
②逆命题是真命题还是假命题?如果是真命题,请画出“图形”,写出“已知”,“求证”,再进行“证明”;如果是假命题,请举反例说明.
21世纪教育网版权所有
考点2:勾股定理的简单计算
【例2】(1)(2013?黔西南州)一直角三角形的两边长分别为3和4.则第三边的长为( )
A.5 B.
C. D.5或
(2)(2012?怀化)等腰三角形的底边长为6,底边上的中线长为4,它的腰长为( )
A.7 B.6 C.5 D.4
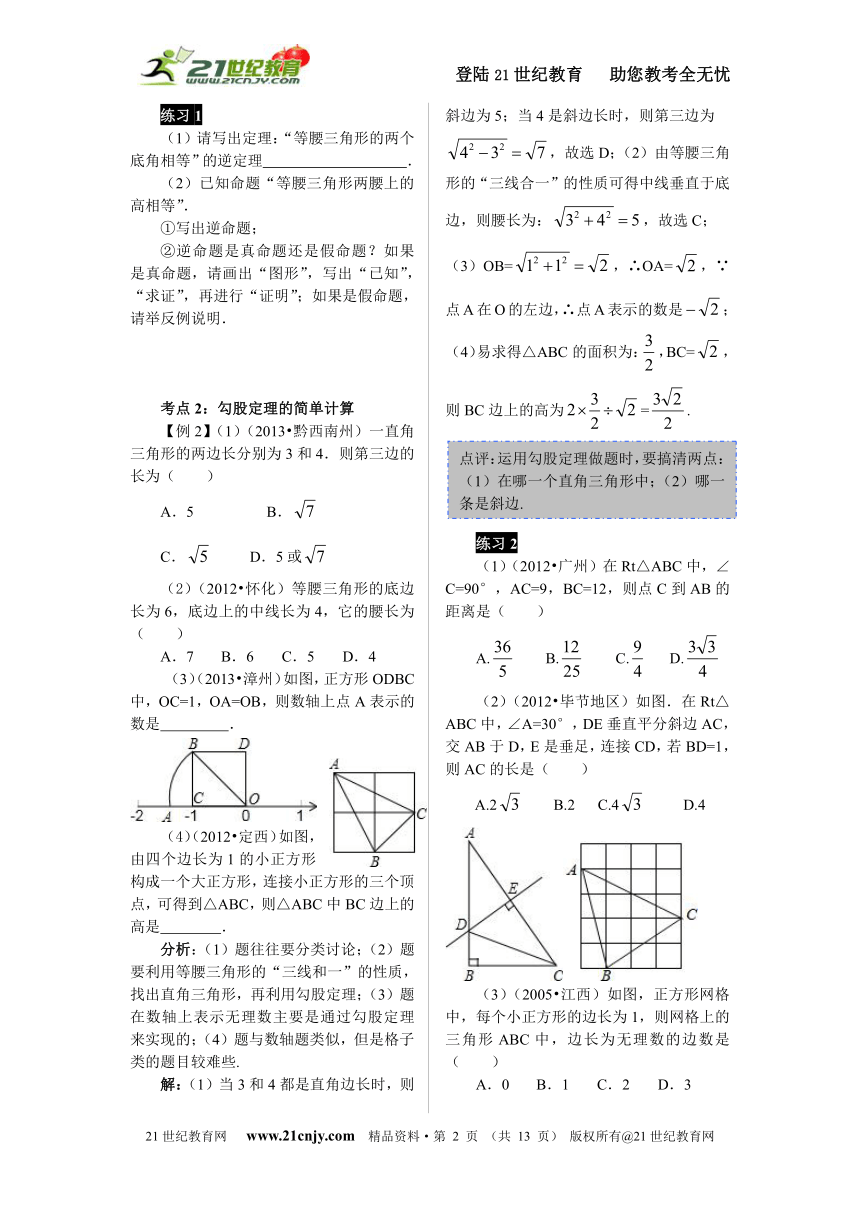
(3)(2013?漳州)如图,正方形ODBC中,OC=1,OA=OB,则数轴上点A表示的数是 .
(4)(2012?定西)如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是 .
分析:(1)题往往要分类讨论;(2)题要利用等腰三角形的“三线和一”的性质,找出直角三角形,再利用勾股定理;(3)题在数轴上表示无理数主要是通过勾股定理来实现的;(4)题与数轴题类似,但是格子类的题目较难些.
解:(1)当3和4都是直角边长时,则斜边为5;当4是斜边长时,则第三边为
,故选D;(2)由等腰三角形的“三线合一”的性质可得中线垂直于底边,则腰长为:,故选C;
OB=,∴OA=,∵点A在O的左边,∴点A表示的数是;
(4)易求得△ABC的面积为:,BC=,则BC边上的高为=.
练习2
(1)(2012?广州)在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. B. C. D.
(2)(2012?毕节地区)如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是( )
A.2 B.2 C.4 D.4
(3)(2005?江西)如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )
A.0 B.1 C.2 D.3
考点3:勾股定理的逆定理的简单计算
【例3】(1)(2006?丽水)如图,以△ABC的三边分别向外作正方形,它们的面积分别是S1,S2,S3,如果S1+S2=S3,那么△ABC的形状是 三角形.
(2)如图所示的一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,则这块地的面积为 m2.
(3)已知a、b、c为△ABC的三边,若a4+b2c2 -a2c2 -b4=0,判断△ABC的形状.
分析:(1)题根据S1+S2=S3可得AB2+BC2=AC2,即可判断;(2)可连接AC,求出边AC,从而证得△ABC是直角三角形,再算边四边形的面积;(3)通过给出的条件,把等式分解变形,找出a,b,c之间的关系,再判定三角形的形状.
解:(1)直角三角形;(2)24m2;
解析:(1)题根据S1+S2=S3可得AB2+BC2=AC2,则由勾股定理的逆定理可得△ABC是直角三角形;(2)可连接AC,在Rt△ADC中,AC=m,∴AC2+BC2=52+122=132=AB2,∴△ABC是直角三角形,则四边形ABCD的面积为:
=24;
(3)由a4+b2c2 -a2c2 -b4=0,
∴c2(b2-a2)+(a2+b2)(a2-b2)=0
∴(b2-a2)[c2-(a2+b2)]=0
∴b2-a2=0或c2-(a2+b2)=0
即b=a或c2=a2+b2
∴ABC为等腰三角形或直角三角形;
练习3
三个半圆的面积分别为S1=4.5π,S2=8π,S3=12.5π,把三个半圆拼成如图所示的图形,则△ABC一定是直角三角形吗?说明理由.
考点4:勾股定理及其逆定理的应用
【例4】(1)(2013?济南)如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为(滑轮上方的部分忽略不计)为( )
A.12m B.13m C.16m D.17m
(2)“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.若“远航”号沿东北方向航行,则“海天”号沿( )
A.西南方向航行
B.西北方向航行
C.东南方向航行
D.西北方向航行或东南方向航行
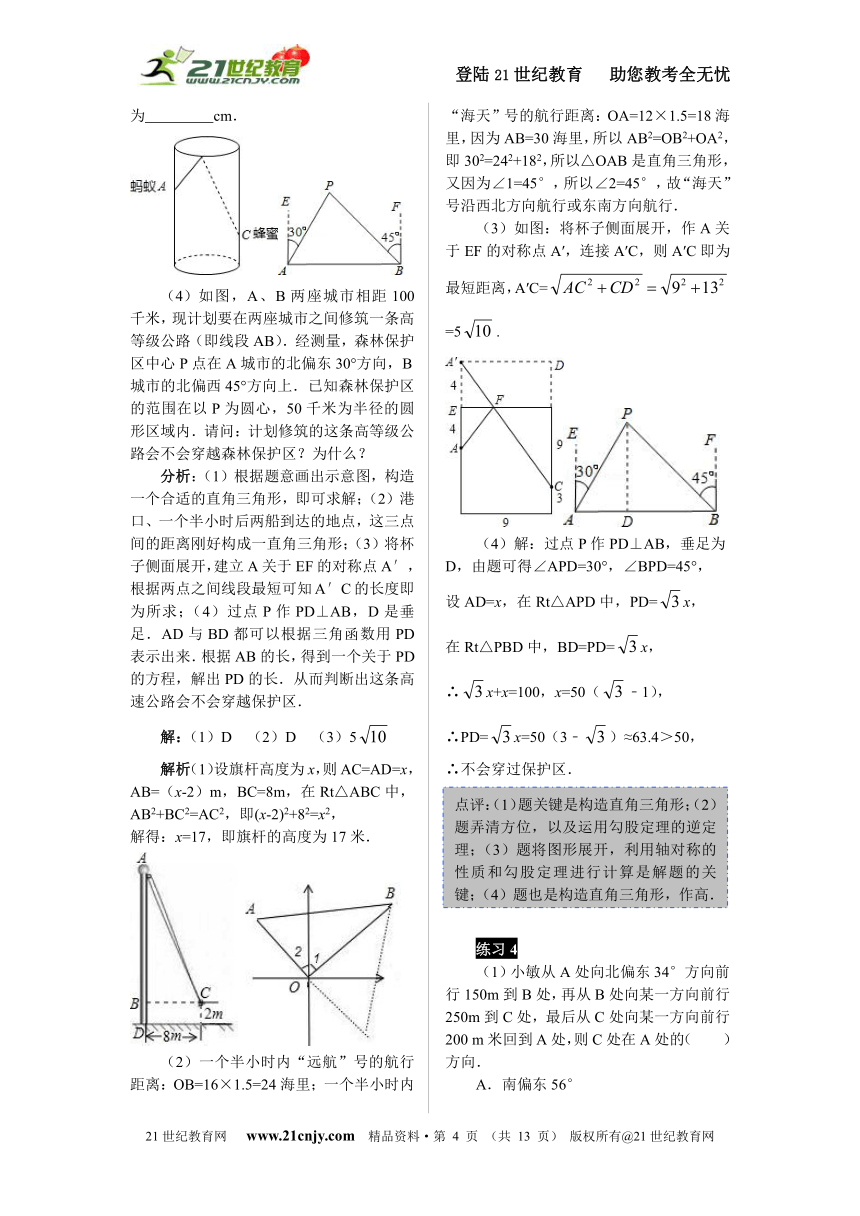
(3)(2012?青岛)如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
如图,A、B两座城市相距100千米,现计划要在两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上.已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越森林保护区?为什么?
分析:(1)根据题意画出示意图,构造一个合适的直角三角形,即可求解;(2)港口、一个半小时后两船到达的地点,这三点间的距离刚好构成一直角三角形;(3)将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′C的长度即为所求;(4)过点P作PD⊥AB,D是垂足.AD与BD都可以根据三角函数用PD表示出来.根据AB的长,得到一个关于PD的方程,解出PD的长.从而判断出这条高速公路会不会穿越保护区.
解:(1)D (2)D (3)5
解析(1)设旗杆高度为x,则AC=AD=x,AB=(x-2)m,BC=8m,在Rt△ABC中,AB2+BC2=AC2,即(x-2)2+82=x2,
解得:x=17,即旗杆的高度为17米.
(2)一个半小时内“远航”号的航行距离:OB=16×1.5=24海里;一个半小时内“海天”号的航行距离:OA=12×1.5=18海里,因为AB=30海里,所以AB2=OB2+OA2,即302=242+182,所以△OAB是直角三角形,
又因为∠1=45°,所以∠2=45°,故“海天”号沿西北方向航行或东南方向航行.
(3)如图:将杯子侧面展开,作A关于EF的对称点A′,连接A′C,则A′C即为最短距离,A′C=
=5.
(4)解:过点P作PD⊥AB,垂足为D,由题可得∠APD=30°,∠BPD=45°,
设AD=x,在Rt△APD中,PD=x,
在Rt△PBD中,BD=PD=x,
∴x+x=100,x=50(﹣1),
∴PD=x=50(3﹣)≈63.4>50,
∴不会穿过保护区.
练习4
(1)小敏从A处向北偏东34°方向前行150m到B处,再从B处向某一方向前行250m到C处,最后从C处向某一方向前行200 m米回到A处,则C处在A处的( )方向.
A.南偏东56°
B.南偏东56°或北偏西56°
C.北偏西34°
D.北偏西34°或南偏东34°
(2)长方形门框ABCD中,AB=2m,AD=1.5m.现有四块长方形薄木板,尺寸分别是:①长1.4m,宽1.2m;②长2.1m,宽1.7m;③长2.7m,宽2.1m;④长3m,宽2.6m.其中不能从门框内通过的木板有( )
A.0块 B.1块 C.2块 D.3块
(3)如图,正方体的棱长为4cm,M是EH的中点,现有一只蚂蚁位于点B处,它想沿正方体的表面爬行到点M处获取食物,则蚂蚁需爬行的最短路程为 cm.
(4)(2002?浙江)由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭.近日,A城气象局测得沙尘暴中心在A城的正西方向240km的B处,以每时12km的速度向北偏东60°方向移动,距沙尘暴中心150km的范围为受影响区域.
①A城是否受到这次沙尘暴的影响?为什么?
②若A城受这次沙尘暴影响,那么遭受影响的时间有多长?
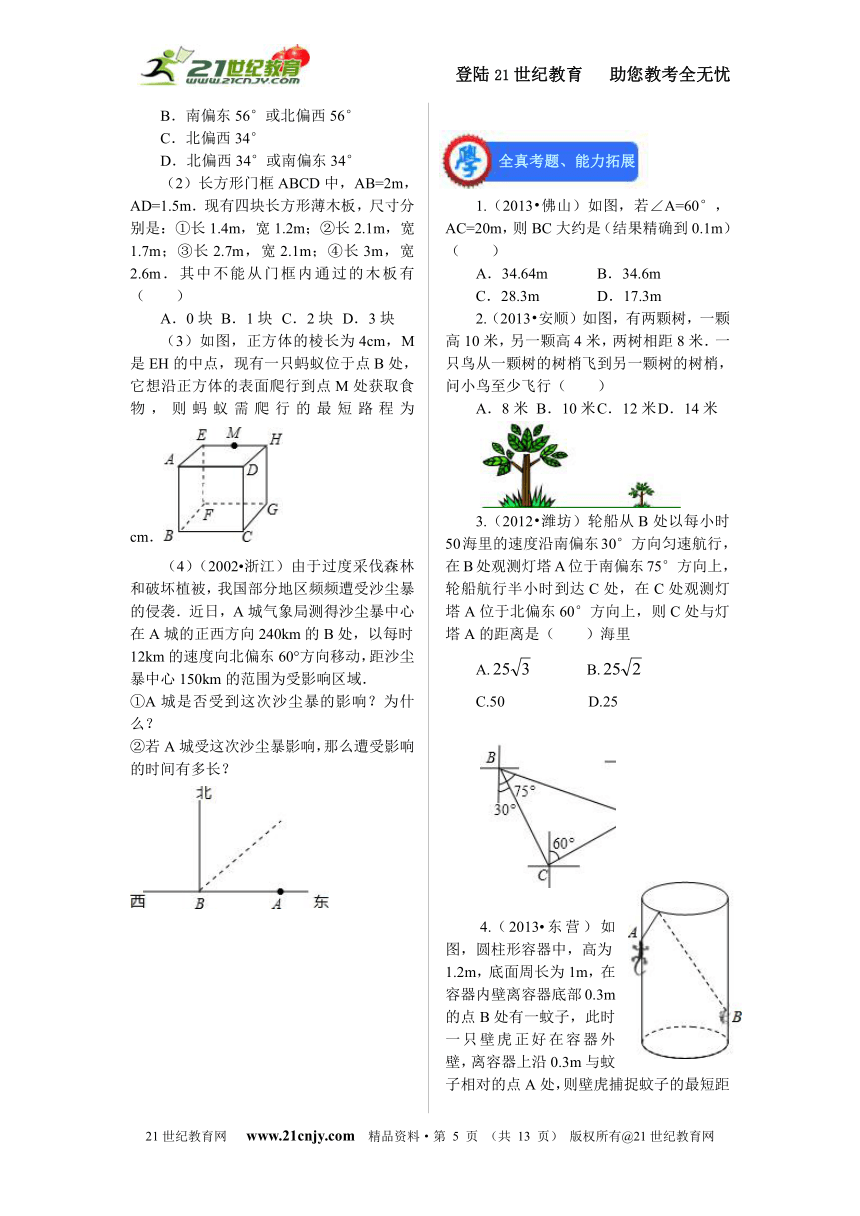
1.(2013?佛山)如图,若∠A=60°,AC=20m,则BC大约是(结果精确到0.1m) ( )
A.34.64m B.34.6m
C.28.3m D.17.3m
2.(2013?安顺)如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行( )
A.8米 B.10米 C.12米 D.14米
(2012?潍坊)轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里
A. B.
C.50 D.25
(2013?东营)如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为
m(容器厚度忽略不计).
5.(2012?泰安)如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2-GE2=EA2.
用时: 分数
一、选择题(每题4分,共32分)
1.如图,△ABC为等腰直角三角形,它的面积为8平方厘米,以它的斜边为边的正方形BCDE的面积为( )平方厘米.
A.16 B.24 C.64 D.32
2.(2011?成华区二模)如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是( )
A.1 B.2 C. D.
3.(2012?黄冈模拟)将边长分别为3cm,3cm,2cm的等腰三角形从一个圆钢圈中穿过,那么这个圆钢圈的最小直径是( )
A.2cm B.2cm
C.3cm D.cm
4.(2010?温州模拟)下列三条线段能构成直角三角形的是( )
A.1cm,2cm,3cm
B.2cm,4cm,5cm
C.6cm,8cm,10cm
D.cm,cm,cm
5.(2012?乐山模拟)一船向东航行,上午8时到达B处,看到有一灯塔在它的南偏东60°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正南方向,则这艘船航行的速度为( )
A.18海里/小时 B.18海里/小时
C.36海里/小时 D.36海里/小时
6.(2007?茂名)如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.12≤a≤13 B.12≤a≤15
C.5≤a≤12 D.5≤a≤13
(2012?北京大兴区一模)如图,圆柱底面直径AB、母线BC均为4cm,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离( )
B.
C. D.
在直角坐标系中点A(2,3)点B (-3,1),在x轴上找一点P,使PA+PB最短,则点P的坐标是( )
A.(2,0) B.(,0)
C.(,0) D.(1,0)
二、填空题(每题3分,共18分)
9. 若△ABC中的三边长分别是9、12、15,则△ABC的面积是 .
10. 在Rt△ABC中,∠C=90°,a、b、c分别△ABC的三条边,已知a+b=7,S△ABC=6,则c= .
11.已知等腰△ABC的底边BC=8,腰长AB=5,一动点P在底边上从点B开始向点C以每秒0.5的速度运动,当点P运动到PA与腰垂直的位置时,点P运动的时间应为
秒.
如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.则当收绳8秒后船向岸边移动了 米(结果保留根号).
13.如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积为24cm2,则AC长是 cm.
如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第2014个等腰直角三角形的面积S2014= .
三、解答题(共40分)
15.(2012?鄂州)小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8,试求BD的长.(10分)
16.(2009?临夏州)如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:(10分)
(1)△ACE≌△BCD;
(2)AD2+DB2=DE2.
17.(2013?本溪)校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,若测得某校车从B到C匀速行驶用时10秒,问这辆车在本路段是否超速?请说明理由(参考数据:=1.41,=1.73)
21世纪教育网版权所有
18.(2010?资阳)在军事上,常用时钟表示方位角(读数对应的时针方向),如正北为12点方向,北偏西30°为11点方向.在一次反恐演习中,甲队员在A处掩护,乙队员从A处沿12点方向以40米/分的速度前进,2分钟后到达B处.这时,甲队员发现在自己的1点方向的C处有恐怖分子,乙队员发现C处位于自己的2点方向(如图).假设距恐怖分子100米以外为安全位置.
(1)乙队员是否处于安全位置?为什么?
(2)因情况不明,甲队员立即发出指令,要求乙队员沿原路后撤,务必于15秒内到达安全位置.为此,乙队员至少应用多快的速度撤离?(结果精确到个位.参考数据:)
21世纪教育网版权所有
21世纪教育网版权所有
21世纪教育网版权所有
参考答案:
练习3 解:∵S1=π()2=4.5π,S2=π()2=8π,S3=π()2=12.5π,∴AC2=36,BC2=64,AB2=100,又∵AC2+BC2=AB2,∴△ABC一定是直角三角形.
练习4 (1)B 【解析】∵AB=150m,BC=250m,AC=200m,2002+1502=62500=2502,即AC2+AB2=BC2,∴△ABC是直角三角形,∴∠BAC为直角,过A向直线AB作垂线,则∠BAC=90°,∠1+∠3=60°,故C处在A处的南偏东56°或北偏西56°.
(2)B 【解析】门框的对角线长是:=2.5m.宽小于或等于2.5m的有:①②③.
(3)如图所示展开:连接BM,则线段BM的长就是蚂蚁需爬行的最短路程,∵正方体的棱长为4cm,M是EH的中点,∴∠Q=90°,BQ=(4+2)cm=6cm,由勾股定理得:BM=2cm.
(4)①过点A作AC⊥BM,垂足为C,在Rt△ABC中,由题意可知∠CBA=30°,∴AC=AB=×240=120,∵AC=120<150,∴A城将受这次沙尘暴的影响;
②设点E,F是以A为圆心,150km为半径的圆与MB的交点,连接AE,AF,
由题意得CE==90,∴EF=2CE=2×90=180,
∴A城受沙尘暴影响的时间为15(时).
全真考题、能力拓展
B 【解析】∵∠A=60°,∠C=90°,∴∠B=30°,∴AB=2AC,∵AC=20m,∴AB=40m,
∴BC=.
B 【解析】如图,设大树高为AB=10m,小树高为CD=4m,过C点作CE⊥AB于E,则EBDC是矩形,连接AC,∴EB=4m,EC=8m,AE=AB﹣EB=10﹣4=6m,在Rt△AEC中,AC==10m.
3.D 【解析】根据题意,∠1=∠2=30°,∵∠ACD=60°,∴∠ACB=30°+60°=90°,
∴∠CBA=75°﹣30°=45°,∴△ABC为等腰直角三角形,∵BC=50×0.5=25,∴AC=BC=25(海里).
4.1.3 【解析】如图:∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,
∴A′D=0.5m,BD=1.2m,∴将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B==1.3(m).
课时自测、认清自我
1.D 【解析】△ABC的面积为:,∴AB=AC=4,由勾股定理得BC=4,正方形BCDE的面积为32平方厘米.
2.B 【解析】∵Rt△ABC中,∠ACB=30°,∴∠ABC=60°,∵BD平分∠ABC,∴∠ABD=∠DBC=30°,∴∠DBC=∠ACB,∴BD=CD=4,在Rt△ABD中,∵∠ABD=30°,∴AD=BD=×4=2,过点D作DE⊥BC于点E,则DE=AD=2.
7.A 【解析】将圆柱展开成平面,A、B、S构成一个直角三角形,且AB=2(半圆),BS=2,则由勾股定理得AS=.
8.B 【解析】∵点A(2,3),∴点A关于x轴的对称点的坐标为(2,﹣3),设直线A′B的解析式为y=kx+b,解得k=,b=∴y=x,∴P的坐标为(,0).
二、9.54 【解析】∵92+122=225=152,∴△ABC是直角三角形,且斜边长为15,则其面积为:54.
10.5 【解析】∵Rt△ABC中,∠C=90°,a+b=7,S△ABC=6,∴ab=6,即ab=12,
∴(a+b)2=a2+b2+2ab=a2+b2+24=49,即a2+b2=25,则根据勾股定理得:c=5.
11.3.5秒或12.5秒 【解析】如图,作AD⊥BC,交BC于点D,∵BC=8cm,∴BD=CD=BC=4cm,∴AD==3,分两种情况:当点P运动t秒后有PA⊥AC时,∵AP2=PD2+AD2=PC2﹣AC2,∴PD2+AD2=PC2﹣AC2,∴PD2+32=(PD+4)2﹣52∴PD=2.25,∴BP=4﹣2.25=1.75=0.5t,∴t=3 5秒;;当点P运动t秒后有PA⊥AB时,同理可证得PD=2.25,∴BP=4+2.25=6.25=0.5t,∴t=12.5秒,∴点P运动的时间为3.5秒或12.5秒.
12.5﹣ 【解析】如图,∵AC=5米,∠B=30°,AC⊥AB,∴BC=2AC=2×5=10米,根据勾股定理,AB===5米,收绳8秒后,设船的位置为B′,∵0.5×8=4米,∴B′C=10﹣4=6米,根据勾股定理,AB′==,故BB′=AB﹣AB′=(5﹣)米.
13.4 【解析】延长CD至点E,使DE=BC,连接AE,∵∠BAD=∠BCD=90°,∴∠2+∠B=180°,∵∠1+∠2=180°,∠2+∠B=180°,∴∠1=∠B,∴△ABC≌△ADE(SAS),∴∠EAD=∠BAC,AC=AE,∵∠BAD=90°,∴∠EAC=90°,∴△ACE是等腰直角三角形,∵四边形ABCD的面积为24cm2,∴AC2=24,解得AC=4cm.
14.22012 【解析】根据直角三角形的面积公式,得S1==2﹣1;根据勾股定理,得:AB=,则S2=1=20;A1B1=2,则S3=21,依此类推,发现:Sn=2n﹣2.故答案为22012.
三、15.解:过点F作FM⊥AD于M,∵∠EDF=90°,∠E=60°,∴∠EFD=30°,∵DE=8,
∴EF=16,∴DF==8,∵EF∥AD,∴∠FDM=30°,∴FM=DF=4,
∴MD==12,∵∠C=45°,∴∠MFB=∠B=45°,∴FM=BM=4,∴BD=DM﹣BM=12﹣4.
16.证明:(1)∵∠ACB=∠ECD=90°,∴∠ACD+∠BCD=∠ACD+∠ACE,即∠BCD=∠ACE.
∵BC=AC,DC=EC,∴△ACE≌△BCD.(2)∵△ACB是等腰直角三角形,∴∠B=∠BAC=45度.∵△ACE≌△BCD,∴∠B=∠CAE=45°∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD2+AE2=DE2.由(1)知AE=DB,∴AD2+DB2=DE2.
17.解:过点D作DE⊥AB于点E,∵∠CDB=75°,∴∠CBD=15°,∠EBD=15°,
在Rt△CBD和Rt△EBD中,∵∴△CBD≌△EBD,
∴CD=DE,在Rt△ADE中,∠A=60°,AD=40米,则AE=20米,由勾股定理得DE=20米,故AC=AD+CD=AD+DE=(40+20)米,在Rt△ABC中,AB=2AC=(80+40)米,则BC=(40+60)米,则速度==4+6≈12.92米/秒,∵12.92米/秒=46.512千米/小时,∴该车没有超速.
18.解:(1)乙队员不安全.易求AB=80米,∵∠DBC=60°,∠BAC=30°,∴∠BCA=∠BAC=30°,∴BC=AB=80米<100米,∴乙队员不安全.
(2)过点C作CD⊥AB,垂足为D,在AB边上取一点B1,使CB1=100米,
在Rt△CBD中,∠CBD=60°,BC=80米,则BD=40米,CD=40米,
在Rt△CDB1中,由勾股定理知B1D==20米,
则BB1=(20﹣40)米,而≈2.13秒,
依题意结果精确到个位,所以乙队员至少应以3米/秒的速度撤离.
第5课时 本章复习
1. 直角三角形的定义、性质:有一角为直角的三角形为直角三角形,其中两个锐角互余.
2.直角三角有关的定理:
(1)直角三角形中,如果一个角为30°,那么它所对的直角边是斜边的一半;
(2)勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么.
(3)勾股定理的逆定理:如果三角形的三边长a,b,c满足,那么这个三角形是直角三角形.(判定直角三角形)
3.等腰直角三角形:等腰直角三角形是特殊的等腰三角形,除了有等腰三角形的性质外,它的顶角为直角,两个锐角都是45°,且其斜边长是直角边长的倍.
4.勾股定理的证明:赵爽弦图(课本23页).21世纪教育网版权所有
5.勾股定理的应用:(1)直角根据勾股定理求直角边或斜边;(2)解决方位类型题;(3)根据定长的位置变化求它的值:如梯子的长,旗杆的长等问题;(3)最短路径:立体展开,求最短路径、平面两点间的最短路径等问题.21世纪教育网版权所有
6.勾股定理的逆定理的应用:判断直角三角形.21世纪教育网版权所有
7.这一章所学的其他概念:
(1)互逆命题:如果两个命题的题设、结论正好相反,那么这两个命题叫做互逆命题;如果把其中一个叫原命题,那么另外一个就是逆命题;
(2)互逆定理:一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理为互逆定理;如勾股定理、勾股定理的逆定理;
(3)勾股数:像15,8,17这样,能够成为直角三角形三条连长的三个正整数,称为勾股数.
8.作图:(1)会画赵爽弦图;(2)会在数轴上表示出带根号的数,如,等.
考点1:逆命题和逆定理
【例1】在下列定理中,没有逆定理的是( )
A.有斜边和一直角边对应相等的两个直角三角形全等
B.直角三角形两个锐角互余
C.全等三角形对应角相等
D.角平分线上的点到这个角两边的距离相等
分析:首先要区分逆命题和逆定理,逆命题是与原命题(成立或不成立)的题设、结论相反的,成立或者不成立;如果某定理的逆命题是成立的,那么该逆命题就是原定理的逆定理;如果该定理的逆命题不成立,那么它就没有逆定理.先写出各选项的逆命题,判断出其真假即可解答.
解:C
解析:A. 其逆命题是“两个直角三角形全等,那么斜边和一直角边对应相等”,正确,所以有逆定理;
B. 其逆命题是“两个锐角互余的三角形是直角三角形”,正确,所以有逆定理;
C. 其逆命题是“对应角相等的三角形是全等三角形”,错误,所以没有逆定理;
D. 其逆命题是“到角两边距离相等的点在角的平分线上”,正确,所以有逆定理.
练习1
(1)请写出定理:“等腰三角形的两个底角相等”的逆定理 .
(2)已知命题“等腰三角形两腰上的高相等”.
①写出逆命题;
②逆命题是真命题还是假命题?如果是真命题,请画出“图形”,写出“已知”,“求证”,再进行“证明”;如果是假命题,请举反例说明.
21世纪教育网版权所有
考点2:勾股定理的简单计算
【例2】(1)(2013?黔西南州)一直角三角形的两边长分别为3和4.则第三边的长为( )
A.5 B.
C. D.5或
(2)(2012?怀化)等腰三角形的底边长为6,底边上的中线长为4,它的腰长为( )
A.7 B.6 C.5 D.4
(3)(2013?漳州)如图,正方形ODBC中,OC=1,OA=OB,则数轴上点A表示的数是 .
(4)(2012?定西)如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是 .
分析:(1)题往往要分类讨论;(2)题要利用等腰三角形的“三线和一”的性质,找出直角三角形,再利用勾股定理;(3)题在数轴上表示无理数主要是通过勾股定理来实现的;(4)题与数轴题类似,但是格子类的题目较难些.
解:(1)当3和4都是直角边长时,则斜边为5;当4是斜边长时,则第三边为
,故选D;(2)由等腰三角形的“三线合一”的性质可得中线垂直于底边,则腰长为:,故选C;
OB=,∴OA=,∵点A在O的左边,∴点A表示的数是;
(4)易求得△ABC的面积为:,BC=,则BC边上的高为=.
练习2
(1)(2012?广州)在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. B. C. D.
(2)(2012?毕节地区)如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是( )
A.2 B.2 C.4 D.4
(3)(2005?江西)如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )
A.0 B.1 C.2 D.3
考点3:勾股定理的逆定理的简单计算
【例3】(1)(2006?丽水)如图,以△ABC的三边分别向外作正方形,它们的面积分别是S1,S2,S3,如果S1+S2=S3,那么△ABC的形状是 三角形.
(2)如图所示的一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,则这块地的面积为 m2.
(3)已知a、b、c为△ABC的三边,若a4+b2c2 -a2c2 -b4=0,判断△ABC的形状.
分析:(1)题根据S1+S2=S3可得AB2+BC2=AC2,即可判断;(2)可连接AC,求出边AC,从而证得△ABC是直角三角形,再算边四边形的面积;(3)通过给出的条件,把等式分解变形,找出a,b,c之间的关系,再判定三角形的形状.
解:(1)直角三角形;(2)24m2;
解析:(1)题根据S1+S2=S3可得AB2+BC2=AC2,则由勾股定理的逆定理可得△ABC是直角三角形;(2)可连接AC,在Rt△ADC中,AC=m,∴AC2+BC2=52+122=132=AB2,∴△ABC是直角三角形,则四边形ABCD的面积为:
=24;
(3)由a4+b2c2 -a2c2 -b4=0,
∴c2(b2-a2)+(a2+b2)(a2-b2)=0
∴(b2-a2)[c2-(a2+b2)]=0
∴b2-a2=0或c2-(a2+b2)=0
即b=a或c2=a2+b2
∴ABC为等腰三角形或直角三角形;
练习3
三个半圆的面积分别为S1=4.5π,S2=8π,S3=12.5π,把三个半圆拼成如图所示的图形,则△ABC一定是直角三角形吗?说明理由.
考点4:勾股定理及其逆定理的应用
【例4】(1)(2013?济南)如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为(滑轮上方的部分忽略不计)为( )
A.12m B.13m C.16m D.17m
(2)“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.若“远航”号沿东北方向航行,则“海天”号沿( )
A.西南方向航行
B.西北方向航行
C.东南方向航行
D.西北方向航行或东南方向航行
(3)(2012?青岛)如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
如图,A、B两座城市相距100千米,现计划要在两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上.已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越森林保护区?为什么?
分析:(1)根据题意画出示意图,构造一个合适的直角三角形,即可求解;(2)港口、一个半小时后两船到达的地点,这三点间的距离刚好构成一直角三角形;(3)将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′C的长度即为所求;(4)过点P作PD⊥AB,D是垂足.AD与BD都可以根据三角函数用PD表示出来.根据AB的长,得到一个关于PD的方程,解出PD的长.从而判断出这条高速公路会不会穿越保护区.
解:(1)D (2)D (3)5
解析(1)设旗杆高度为x,则AC=AD=x,AB=(x-2)m,BC=8m,在Rt△ABC中,AB2+BC2=AC2,即(x-2)2+82=x2,
解得:x=17,即旗杆的高度为17米.
(2)一个半小时内“远航”号的航行距离:OB=16×1.5=24海里;一个半小时内“海天”号的航行距离:OA=12×1.5=18海里,因为AB=30海里,所以AB2=OB2+OA2,即302=242+182,所以△OAB是直角三角形,
又因为∠1=45°,所以∠2=45°,故“海天”号沿西北方向航行或东南方向航行.
(3)如图:将杯子侧面展开,作A关于EF的对称点A′,连接A′C,则A′C即为最短距离,A′C=
=5.
(4)解:过点P作PD⊥AB,垂足为D,由题可得∠APD=30°,∠BPD=45°,
设AD=x,在Rt△APD中,PD=x,
在Rt△PBD中,BD=PD=x,
∴x+x=100,x=50(﹣1),
∴PD=x=50(3﹣)≈63.4>50,
∴不会穿过保护区.
练习4
(1)小敏从A处向北偏东34°方向前行150m到B处,再从B处向某一方向前行250m到C处,最后从C处向某一方向前行200 m米回到A处,则C处在A处的( )方向.
A.南偏东56°
B.南偏东56°或北偏西56°
C.北偏西34°
D.北偏西34°或南偏东34°
(2)长方形门框ABCD中,AB=2m,AD=1.5m.现有四块长方形薄木板,尺寸分别是:①长1.4m,宽1.2m;②长2.1m,宽1.7m;③长2.7m,宽2.1m;④长3m,宽2.6m.其中不能从门框内通过的木板有( )
A.0块 B.1块 C.2块 D.3块
(3)如图,正方体的棱长为4cm,M是EH的中点,现有一只蚂蚁位于点B处,它想沿正方体的表面爬行到点M处获取食物,则蚂蚁需爬行的最短路程为 cm.
(4)(2002?浙江)由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭.近日,A城气象局测得沙尘暴中心在A城的正西方向240km的B处,以每时12km的速度向北偏东60°方向移动,距沙尘暴中心150km的范围为受影响区域.
①A城是否受到这次沙尘暴的影响?为什么?
②若A城受这次沙尘暴影响,那么遭受影响的时间有多长?
1.(2013?佛山)如图,若∠A=60°,AC=20m,则BC大约是(结果精确到0.1m) ( )
A.34.64m B.34.6m
C.28.3m D.17.3m
2.(2013?安顺)如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行( )
A.8米 B.10米 C.12米 D.14米
(2012?潍坊)轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里
A. B.
C.50 D.25
(2013?东营)如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为
m(容器厚度忽略不计).
5.(2012?泰安)如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2-GE2=EA2.
用时: 分数
一、选择题(每题4分,共32分)
1.如图,△ABC为等腰直角三角形,它的面积为8平方厘米,以它的斜边为边的正方形BCDE的面积为( )平方厘米.
A.16 B.24 C.64 D.32
2.(2011?成华区二模)如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是( )
A.1 B.2 C. D.
3.(2012?黄冈模拟)将边长分别为3cm,3cm,2cm的等腰三角形从一个圆钢圈中穿过,那么这个圆钢圈的最小直径是( )
A.2cm B.2cm
C.3cm D.cm
4.(2010?温州模拟)下列三条线段能构成直角三角形的是( )
A.1cm,2cm,3cm
B.2cm,4cm,5cm
C.6cm,8cm,10cm
D.cm,cm,cm
5.(2012?乐山模拟)一船向东航行,上午8时到达B处,看到有一灯塔在它的南偏东60°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正南方向,则这艘船航行的速度为( )
A.18海里/小时 B.18海里/小时
C.36海里/小时 D.36海里/小时
6.(2007?茂名)如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.12≤a≤13 B.12≤a≤15
C.5≤a≤12 D.5≤a≤13
(2012?北京大兴区一模)如图,圆柱底面直径AB、母线BC均为4cm,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离( )
B.
C. D.
在直角坐标系中点A(2,3)点B (-3,1),在x轴上找一点P,使PA+PB最短,则点P的坐标是( )
A.(2,0) B.(,0)
C.(,0) D.(1,0)
二、填空题(每题3分,共18分)
9. 若△ABC中的三边长分别是9、12、15,则△ABC的面积是 .
10. 在Rt△ABC中,∠C=90°,a、b、c分别△ABC的三条边,已知a+b=7,S△ABC=6,则c= .
11.已知等腰△ABC的底边BC=8,腰长AB=5,一动点P在底边上从点B开始向点C以每秒0.5的速度运动,当点P运动到PA与腰垂直的位置时,点P运动的时间应为
秒.
如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.则当收绳8秒后船向岸边移动了 米(结果保留根号).
13.如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积为24cm2,则AC长是 cm.
如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第2014个等腰直角三角形的面积S2014= .
三、解答题(共40分)
15.(2012?鄂州)小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8,试求BD的长.(10分)
16.(2009?临夏州)如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:(10分)
(1)△ACE≌△BCD;
(2)AD2+DB2=DE2.
17.(2013?本溪)校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,若测得某校车从B到C匀速行驶用时10秒,问这辆车在本路段是否超速?请说明理由(参考数据:=1.41,=1.73)
21世纪教育网版权所有
18.(2010?资阳)在军事上,常用时钟表示方位角(读数对应的时针方向),如正北为12点方向,北偏西30°为11点方向.在一次反恐演习中,甲队员在A处掩护,乙队员从A处沿12点方向以40米/分的速度前进,2分钟后到达B处.这时,甲队员发现在自己的1点方向的C处有恐怖分子,乙队员发现C处位于自己的2点方向(如图).假设距恐怖分子100米以外为安全位置.
(1)乙队员是否处于安全位置?为什么?
(2)因情况不明,甲队员立即发出指令,要求乙队员沿原路后撤,务必于15秒内到达安全位置.为此,乙队员至少应用多快的速度撤离?(结果精确到个位.参考数据:)
21世纪教育网版权所有
21世纪教育网版权所有
21世纪教育网版权所有
参考答案:
练习3 解:∵S1=π()2=4.5π,S2=π()2=8π,S3=π()2=12.5π,∴AC2=36,BC2=64,AB2=100,又∵AC2+BC2=AB2,∴△ABC一定是直角三角形.
练习4 (1)B 【解析】∵AB=150m,BC=250m,AC=200m,2002+1502=62500=2502,即AC2+AB2=BC2,∴△ABC是直角三角形,∴∠BAC为直角,过A向直线AB作垂线,则∠BAC=90°,∠1+∠3=60°,故C处在A处的南偏东56°或北偏西56°.
(2)B 【解析】门框的对角线长是:=2.5m.宽小于或等于2.5m的有:①②③.
(3)如图所示展开:连接BM,则线段BM的长就是蚂蚁需爬行的最短路程,∵正方体的棱长为4cm,M是EH的中点,∴∠Q=90°,BQ=(4+2)cm=6cm,由勾股定理得:BM=2cm.
(4)①过点A作AC⊥BM,垂足为C,在Rt△ABC中,由题意可知∠CBA=30°,∴AC=AB=×240=120,∵AC=120<150,∴A城将受这次沙尘暴的影响;
②设点E,F是以A为圆心,150km为半径的圆与MB的交点,连接AE,AF,
由题意得CE==90,∴EF=2CE=2×90=180,
∴A城受沙尘暴影响的时间为15(时).
全真考题、能力拓展
B 【解析】∵∠A=60°,∠C=90°,∴∠B=30°,∴AB=2AC,∵AC=20m,∴AB=40m,
∴BC=.
B 【解析】如图,设大树高为AB=10m,小树高为CD=4m,过C点作CE⊥AB于E,则EBDC是矩形,连接AC,∴EB=4m,EC=8m,AE=AB﹣EB=10﹣4=6m,在Rt△AEC中,AC==10m.
3.D 【解析】根据题意,∠1=∠2=30°,∵∠ACD=60°,∴∠ACB=30°+60°=90°,
∴∠CBA=75°﹣30°=45°,∴△ABC为等腰直角三角形,∵BC=50×0.5=25,∴AC=BC=25(海里).
4.1.3 【解析】如图:∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,
∴A′D=0.5m,BD=1.2m,∴将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B==1.3(m).
课时自测、认清自我
1.D 【解析】△ABC的面积为:,∴AB=AC=4,由勾股定理得BC=4,正方形BCDE的面积为32平方厘米.
2.B 【解析】∵Rt△ABC中,∠ACB=30°,∴∠ABC=60°,∵BD平分∠ABC,∴∠ABD=∠DBC=30°,∴∠DBC=∠ACB,∴BD=CD=4,在Rt△ABD中,∵∠ABD=30°,∴AD=BD=×4=2,过点D作DE⊥BC于点E,则DE=AD=2.
7.A 【解析】将圆柱展开成平面,A、B、S构成一个直角三角形,且AB=2(半圆),BS=2,则由勾股定理得AS=.
8.B 【解析】∵点A(2,3),∴点A关于x轴的对称点的坐标为(2,﹣3),设直线A′B的解析式为y=kx+b,解得k=,b=∴y=x,∴P的坐标为(,0).
二、9.54 【解析】∵92+122=225=152,∴△ABC是直角三角形,且斜边长为15,则其面积为:54.
10.5 【解析】∵Rt△ABC中,∠C=90°,a+b=7,S△ABC=6,∴ab=6,即ab=12,
∴(a+b)2=a2+b2+2ab=a2+b2+24=49,即a2+b2=25,则根据勾股定理得:c=5.
11.3.5秒或12.5秒 【解析】如图,作AD⊥BC,交BC于点D,∵BC=8cm,∴BD=CD=BC=4cm,∴AD==3,分两种情况:当点P运动t秒后有PA⊥AC时,∵AP2=PD2+AD2=PC2﹣AC2,∴PD2+AD2=PC2﹣AC2,∴PD2+32=(PD+4)2﹣52∴PD=2.25,∴BP=4﹣2.25=1.75=0.5t,∴t=3 5秒;;当点P运动t秒后有PA⊥AB时,同理可证得PD=2.25,∴BP=4+2.25=6.25=0.5t,∴t=12.5秒,∴点P运动的时间为3.5秒或12.5秒.
12.5﹣ 【解析】如图,∵AC=5米,∠B=30°,AC⊥AB,∴BC=2AC=2×5=10米,根据勾股定理,AB===5米,收绳8秒后,设船的位置为B′,∵0.5×8=4米,∴B′C=10﹣4=6米,根据勾股定理,AB′==,故BB′=AB﹣AB′=(5﹣)米.
13.4 【解析】延长CD至点E,使DE=BC,连接AE,∵∠BAD=∠BCD=90°,∴∠2+∠B=180°,∵∠1+∠2=180°,∠2+∠B=180°,∴∠1=∠B,∴△ABC≌△ADE(SAS),∴∠EAD=∠BAC,AC=AE,∵∠BAD=90°,∴∠EAC=90°,∴△ACE是等腰直角三角形,∵四边形ABCD的面积为24cm2,∴AC2=24,解得AC=4cm.
14.22012 【解析】根据直角三角形的面积公式,得S1==2﹣1;根据勾股定理,得:AB=,则S2=1=20;A1B1=2,则S3=21,依此类推,发现:Sn=2n﹣2.故答案为22012.
三、15.解:过点F作FM⊥AD于M,∵∠EDF=90°,∠E=60°,∴∠EFD=30°,∵DE=8,
∴EF=16,∴DF==8,∵EF∥AD,∴∠FDM=30°,∴FM=DF=4,
∴MD==12,∵∠C=45°,∴∠MFB=∠B=45°,∴FM=BM=4,∴BD=DM﹣BM=12﹣4.
16.证明:(1)∵∠ACB=∠ECD=90°,∴∠ACD+∠BCD=∠ACD+∠ACE,即∠BCD=∠ACE.
∵BC=AC,DC=EC,∴△ACE≌△BCD.(2)∵△ACB是等腰直角三角形,∴∠B=∠BAC=45度.∵△ACE≌△BCD,∴∠B=∠CAE=45°∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD2+AE2=DE2.由(1)知AE=DB,∴AD2+DB2=DE2.
17.解:过点D作DE⊥AB于点E,∵∠CDB=75°,∴∠CBD=15°,∠EBD=15°,
在Rt△CBD和Rt△EBD中,∵∴△CBD≌△EBD,
∴CD=DE,在Rt△ADE中,∠A=60°,AD=40米,则AE=20米,由勾股定理得DE=20米,故AC=AD+CD=AD+DE=(40+20)米,在Rt△ABC中,AB=2AC=(80+40)米,则BC=(40+60)米,则速度==4+6≈12.92米/秒,∵12.92米/秒=46.512千米/小时,∴该车没有超速.
18.解:(1)乙队员不安全.易求AB=80米,∵∠DBC=60°,∠BAC=30°,∴∠BCA=∠BAC=30°,∴BC=AB=80米<100米,∴乙队员不安全.
(2)过点C作CD⊥AB,垂足为D,在AB边上取一点B1,使CB1=100米,
在Rt△CBD中,∠CBD=60°,BC=80米,则BD=40米,CD=40米,
在Rt△CDB1中,由勾股定理知B1D==20米,
则BB1=(20﹣40)米,而≈2.13秒,
依题意结果精确到个位,所以乙队员至少应以3米/秒的速度撤离.
