6.3.1 二项式定理课前导学 学案(含答案)
文档属性
| 名称 | 6.3.1 二项式定理课前导学 学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 89.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-11 14:01:37 | ||
图片预览

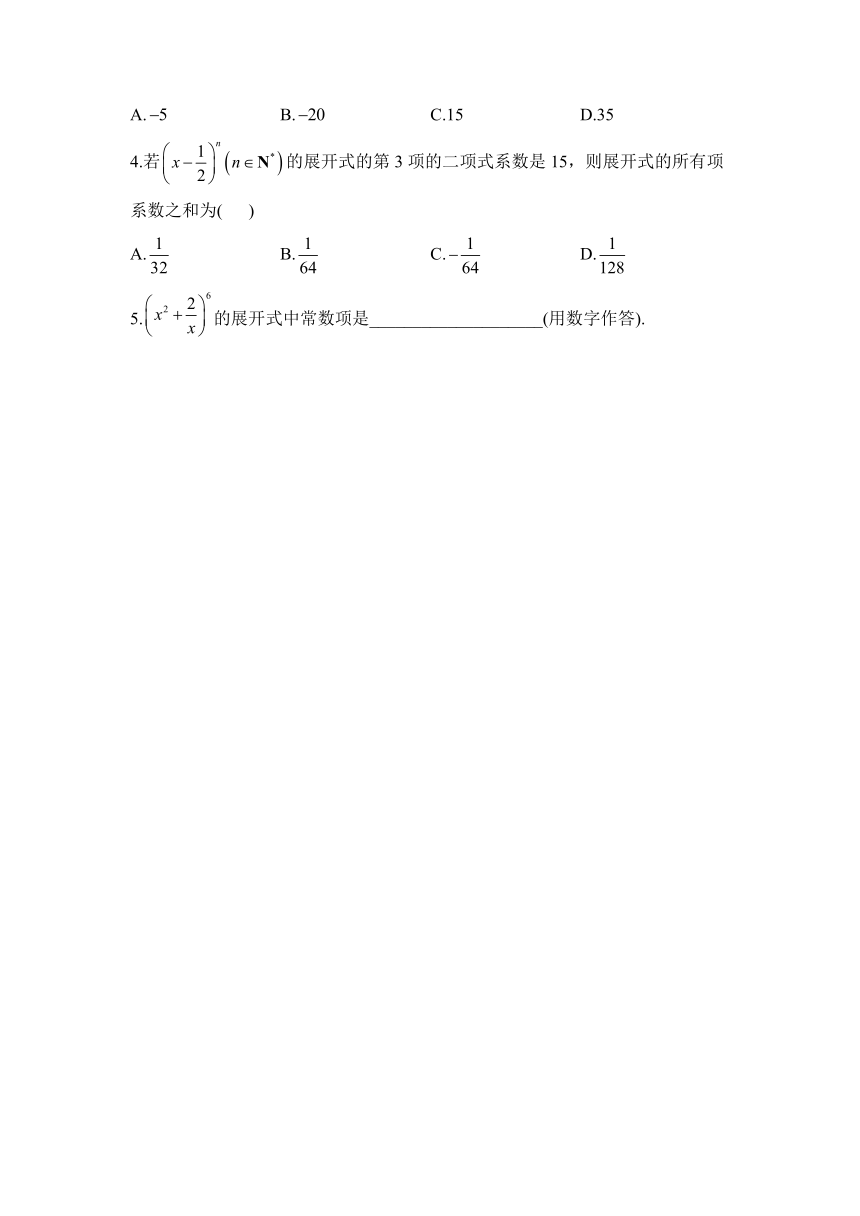
文档简介
6.3.1 二项式定理
—— 高二数学人教A版(2019)
选择性必修第三册课前导学
一、新知自学
公式,叫做_____________,右边的多项式叫做的_____________,其中各项的系数叫做_____________.式中的叫做二项展开式的_________,用表示,即通项为展开式的第项:_____________.
二、问题思考
1.利用二项式定理解题的思路是什么?
2.如何求二项展开式特定项?
3.利用二项式定理证明或判断整除问题的一般方法是什么?
三、练习检测
1.的二项展开式中,第4项是( )
A. B. C. D.
2.的展开式中的系数是( )
A.5103 B.21 C. D.945
3.已知,若,则( )
A. B. C.15 D.35
4.若的展开式的第3项的二项式系数是15,则展开式的所有项系数之和为( )
A. B. C. D.
5.的展开式中常数项是____________________(用数字作答).
【答案及解析】
一、新知自学
二项式定理 二项展开式 二项式系数 通项
二、问题思考
1.(1)求二项展开式时,要根据公式利用组合数系数作为因子写出各项,然后化简得结果.
(2)逆用二项式定理可将一些特殊的多项式化简,其方法是将多项式的项数、各项的系数及幂指数等构造成满足二项展开式的结构特征,即可逆用二项式定理将多项式化为的形式.
2.利用二项展开式的通项可以求二项展开式中任一特定项,如常数项、有理项等.解题时务必须注意:(1)是求某个特定项还是求其系数;(2)是指展开式中的第项,而非第r项;(3)有些特定项不知道是第几项,需要列出r的方程解出r,进而得.
3.(1)变形:将幂底数写成两个数之和,其中一个数是除数的倍数或k次方根;
(2)展开:将变形后的式子按二项式定理展开;
(3)判断:判断或证明展开式中各项均能被除数整除;
(4)下结论.
三、练习检测
1.答案:C
解析:展开式的通项为,所以第4项为.故选C.
2.答案:D
解析:的展开式的通项是,
令,解得,所以展开式中的系数是.故选D.
3.答案:A
解析:由题意,令,可得,解得,,
∴展开式中的系数为,故选A.
4.答案:B
解析:由题意知,解得或(舍去),故,令,得所有项系数之和为.
5.答案:240
解析:展开式的通项为,令,解得,故常数项为.
—— 高二数学人教A版(2019)
选择性必修第三册课前导学
一、新知自学
公式,叫做_____________,右边的多项式叫做的_____________,其中各项的系数叫做_____________.式中的叫做二项展开式的_________,用表示,即通项为展开式的第项:_____________.
二、问题思考
1.利用二项式定理解题的思路是什么?
2.如何求二项展开式特定项?
3.利用二项式定理证明或判断整除问题的一般方法是什么?
三、练习检测
1.的二项展开式中,第4项是( )
A. B. C. D.
2.的展开式中的系数是( )
A.5103 B.21 C. D.945
3.已知,若,则( )
A. B. C.15 D.35
4.若的展开式的第3项的二项式系数是15,则展开式的所有项系数之和为( )
A. B. C. D.
5.的展开式中常数项是____________________(用数字作答).
【答案及解析】
一、新知自学
二项式定理 二项展开式 二项式系数 通项
二、问题思考
1.(1)求二项展开式时,要根据公式利用组合数系数作为因子写出各项,然后化简得结果.
(2)逆用二项式定理可将一些特殊的多项式化简,其方法是将多项式的项数、各项的系数及幂指数等构造成满足二项展开式的结构特征,即可逆用二项式定理将多项式化为的形式.
2.利用二项展开式的通项可以求二项展开式中任一特定项,如常数项、有理项等.解题时务必须注意:(1)是求某个特定项还是求其系数;(2)是指展开式中的第项,而非第r项;(3)有些特定项不知道是第几项,需要列出r的方程解出r,进而得.
3.(1)变形:将幂底数写成两个数之和,其中一个数是除数的倍数或k次方根;
(2)展开:将变形后的式子按二项式定理展开;
(3)判断:判断或证明展开式中各项均能被除数整除;
(4)下结论.
三、练习检测
1.答案:C
解析:展开式的通项为,所以第4项为.故选C.
2.答案:D
解析:的展开式的通项是,
令,解得,所以展开式中的系数是.故选D.
3.答案:A
解析:由题意,令,可得,解得,,
∴展开式中的系数为,故选A.
4.答案:B
解析:由题意知,解得或(舍去),故,令,得所有项系数之和为.
5.答案:240
解析:展开式的通项为,令,解得,故常数项为.
