人教版(2019)新教材高中物理必修2 8.3 动能和动能定理课件(共23张PPT)
文档属性
| 名称 | 人教版(2019)新教材高中物理必修2 8.3 动能和动能定理课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-11 15:25:09 | ||
图片预览







文档简介
(共23张PPT)
动能和动能定理
初中学习过:
1. 物体由于运动而具有的能叫作动能;
2. 物体的动能与质量、速度有关。物体的质量越大,速度越大,则动能越大。
资料
资料
资料
物体动能的变化与力对物体做的功有关。
资料
资料
资料
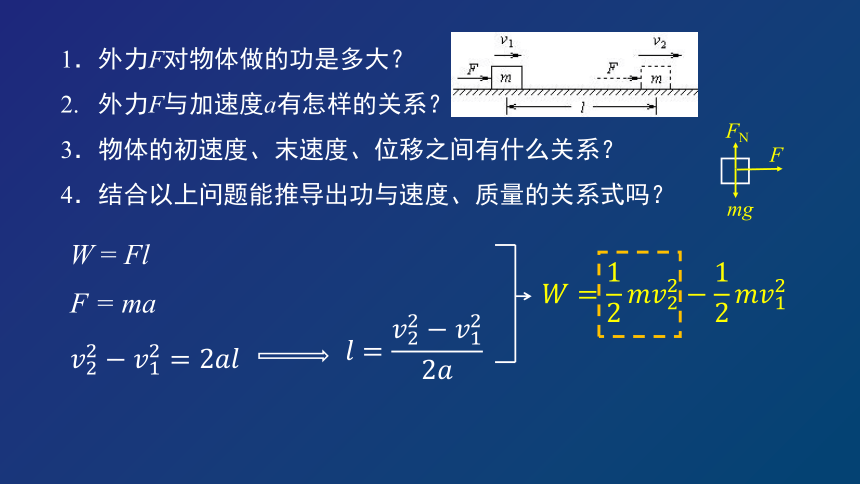
问题1:光滑水平面上,质量为m的物体,在与运动方向相同的恒力F 的作用下发生一段位移l,速度由v1增加到v2。求这个过程中外力对物体做的功(用m、v1、v2表示)。
1.外力F对物体做的功是多大?
2. 外力F与加速度a有怎样的关系?
3.物体的初速度、末速度、位移之间有什么关系?
4.结合以上问题能推导出功与速度、质量的关系式吗?
W = Fl
F = ma
mg
FN
F
1.外力F对物体做的功是多大?
2. 外力F与加速度a有怎样的关系?
3.物体的初速度、末速度、位移之间有什么关系?
4.结合以上问题能推导出功与速度、质量的关系式吗?
一、动能:(Ek)
1. 物体由于运动而具有的能叫做动能
2. 表达式:
3. 国际单位:
1kg·m2/s2
4. 动能是状态量。
焦耳(J)
=1Nm
1J=
5. 动能是标量。
问题:对于质量一定的物体
(1)动能变化,速度是否一定变化?
(2)速度变化,动能是否一定变化?
6. 动能的变化:
v
v
v
否
是
ΔEk = Ek末Ek初
= Ek末Ek初
二、动能定理
1. 内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化。
2. 表达式:
Ek末Ek初
或
ΔEk
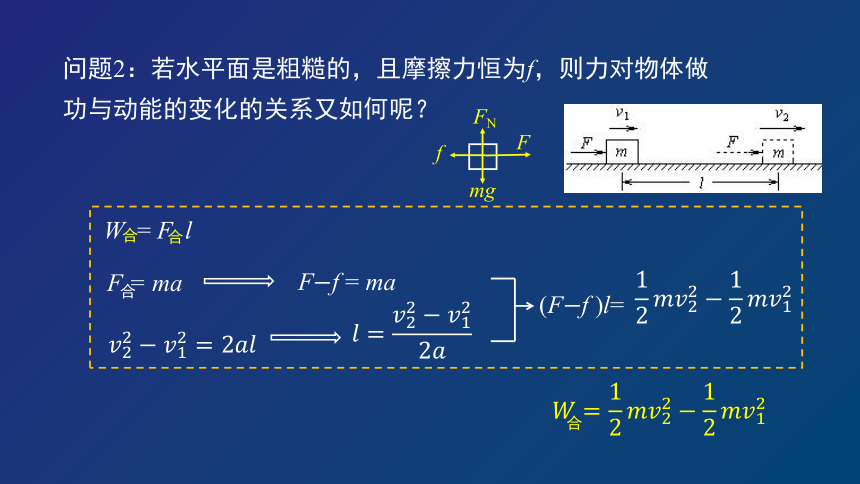
问题2:若水平面是粗糙的,且摩擦力恒为f,则力对物体做功与动能的变化的关系又如何呢?
F
mg
FN
f
W = F l
F = ma
Ff = ma
合
(Ff )l=
合
合
合
(1)如果物体受到几个力的共同作用,动能定理中的力对物体做的功W即为合力的功,它等于各个力做功的代数和。
3. 理解:
(2)当合力对物体做正功时,物体动能增加。
当合力对物体做负功时,物体动能减少。
演绎推理——科学方法
Ek末Ek初
4. 适用范围:
1→2的过程:
1
2
3
4
5
N-1
Ek2Ek1;
既适用于直线运动,也适用于曲线运动。
2→3的过程:
Ek3Ek2;
3→4的过程:
Ek4Ek3;
4→5的过程:
Ek5Ek4;
N-1→N的过程:
EkNEk(N-1)
全过程:
既适用于恒力做功,也适用于变力做功。
N
……
5. 应用动能定理解题的一般步骤:
①确定研究对象。
②通过受力分析、运动分析对物理情景进行分析,画出物体运动的示意图。
③确定研究过程及初末状态,分析该过程中各力做的功及初末状态的动能。
④根据动能定理列方程,然后求解。并对结果进行必要的讨论。
例:一架喷气式飞机,质量m为7.0×104 kg,起飞过程中从静止开始滑跑。当位移l达到2.5×103 m时,速度达到起飞速度80 m/s。在此过程中,飞机受到的平均阻力是飞机所受重力的 。g取10 m/s2,求飞机平均牵引力的大小。
解:以飞机为研究对象
ΔEk
F
mg
FN
kmg
v
l
( F-kmg )
F=1.04×105 N
v0=0
0
资料
l
例:质量为8 g的子弹,以300 m/s的速度射入厚度为5 cm的固定木板(如图所示),射穿后的速度是100 m/s。子弹射穿木板的过程中受到的平均阻力是多大?
f
v
ΔEk
f l
f ×103 N
解:以子弹为研究对象
资料
例:民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面,若斜面高 3.2 m,斜面长6.5 m,质量为60 kg的人沿斜面滑下时所受的阻力是240 N,求人滑至底端时的速度大小,g取10 m/s2。
H
L
v0=0
θ
方法一:牛顿第二定律+运动学规律
mg
FN
f
v=?
例:民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面,若斜面高 3.2 m,斜面长6.5 m,质量为60 kg的人沿斜面滑下时所受的阻力是240 N,求人滑至底端时的速度大小,g取10 m/s2。请用动能定理解答。
H
L
v0=0
θ
方法二:动能定理
mg
FN
f
ΔEk
WG+Wf
mgH f l
0
v=?
解:以人和滑雪板为研究对象
ΔEk
mgh +Wf
0
Wf J
例:哈尔滨第24届世界大学生冬运会某滑雪道为曲线轨道,滑雪道长
s=2.5×103 m,竖直高度h=720 m。运动员从该滑道顶端由静止开始滑下,经t=200s到达滑雪道底端时速度v=30 m/s,人和滑雪板的总质量
m=80 kg,取g=10 m/s2,求人和滑雪板在滑动过程中克服阻力做的功.
mg
FN
人和滑雪板克服阻力做的功为 J
f
资料
例:人们有时用“打夯”的方式把松散的地面夯实(如图所示)。设某次打夯符合以下模型:两人同时通过绳子对重物各施加一个力,力的大小均为320 N,方向都与竖直方向成37°,重物离开地面30 cm后人停止施力,最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg,
g取10 m/s2, cos 37°=0.8。求:
(1)重物刚落地时的速度是多大?
(2)重物对地面的平均冲击力是多大?
分析过程:
① 加速上升( A→B )
H
v0=0
B
A
vB
mg
vA
C
h
vC=0
② 竖直上抛,返回地面( B→A)
③ 减速下降( A→ C)
例:两人同时通过绳子对重物各施加一个力,力的大小均为320 N,方向都与竖直方向成37°,重物离开地面30 cm后人停止施力,最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg, g取10 m/s2, cos 37°=0.8。求:
(1)重物刚落地时的速度是多大?
vA
解:以A→B →A为研究过程
ΔEk
H
v0=0
B
A
vB
mg
T
T
θ
T合
mg
T合H
(2Tcosθ)H
0
例:两人同时通过绳子对重物各施加一个力,力的大小均为320 N,方向都与竖直方向成37°,重物离开地面30 cm后人停止施力,最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg, g取10 m/s2, cos 37°=0.8。求:
以A→C为研究过程
解:
ΔEk
WG+WF
mg
F
mgh Fh
= 0
F=8.18×103 N
H
v0=0
B
A
vB
vA
C
h
vC=0
(2)重物对地面的平均冲击力是多大?
根据牛顿第三定律,重物对地面的平均冲击力大小为8.18×103 N
根据牛顿第三定律,重物对地面的平均冲击力大小为8.18×103 N
例:两人同时通过绳子对重物各施加一个力,力的大小均为320 N,方向都与竖直方向成37°,重物离开地面30 cm后人停止施力,最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg, g取10 m/s2, cos 37°=0.8。求:
mg
F
H
v0=0
B
A
vB
vA
C
h
vC=0
(2)重物对地面的平均冲击力是多大?
对全过程(A→ B→ C)
解法二:
ΔEk
WT +WG+WF
T合H+mgh Fh
F=8.18×103 N
= 0
mg
T
T
θ
T合
mg
课堂小结
动能
动能定理
1. 物体由于运动而具有的能叫做动能
2. 表达式:
3. 国际单位:
焦耳(J)
4. 动能是标量、状态量
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化。
2.表达式:
Ek末Ek初
或
ΔEk
3. 适用范围:
直线、曲线;
恒力、变力。
4. 应用动能定理解决问题。
课后作业:
1. 分析教材第88页第1题、第2题;第100页第2题、第4题。
2. 查阅资料,了解动能定理在解决哪些实际的力学问题中,得到了应用?
山东舰
资料
动能和动能定理
初中学习过:
1. 物体由于运动而具有的能叫作动能;
2. 物体的动能与质量、速度有关。物体的质量越大,速度越大,则动能越大。
资料
资料
资料
物体动能的变化与力对物体做的功有关。
资料
资料
资料
问题1:光滑水平面上,质量为m的物体,在与运动方向相同的恒力F 的作用下发生一段位移l,速度由v1增加到v2。求这个过程中外力对物体做的功(用m、v1、v2表示)。
1.外力F对物体做的功是多大?
2. 外力F与加速度a有怎样的关系?
3.物体的初速度、末速度、位移之间有什么关系?
4.结合以上问题能推导出功与速度、质量的关系式吗?
W = Fl
F = ma
mg
FN
F
1.外力F对物体做的功是多大?
2. 外力F与加速度a有怎样的关系?
3.物体的初速度、末速度、位移之间有什么关系?
4.结合以上问题能推导出功与速度、质量的关系式吗?
一、动能:(Ek)
1. 物体由于运动而具有的能叫做动能
2. 表达式:
3. 国际单位:
1kg·m2/s2
4. 动能是状态量。
焦耳(J)
=1Nm
1J=
5. 动能是标量。
问题:对于质量一定的物体
(1)动能变化,速度是否一定变化?
(2)速度变化,动能是否一定变化?
6. 动能的变化:
v
v
v
否
是
ΔEk = Ek末Ek初
= Ek末Ek初
二、动能定理
1. 内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化。
2. 表达式:
Ek末Ek初
或
ΔEk
问题2:若水平面是粗糙的,且摩擦力恒为f,则力对物体做功与动能的变化的关系又如何呢?
F
mg
FN
f
W = F l
F = ma
Ff = ma
合
(Ff )l=
合
合
合
(1)如果物体受到几个力的共同作用,动能定理中的力对物体做的功W即为合力的功,它等于各个力做功的代数和。
3. 理解:
(2)当合力对物体做正功时,物体动能增加。
当合力对物体做负功时,物体动能减少。
演绎推理——科学方法
Ek末Ek初
4. 适用范围:
1→2的过程:
1
2
3
4
5
N-1
Ek2Ek1;
既适用于直线运动,也适用于曲线运动。
2→3的过程:
Ek3Ek2;
3→4的过程:
Ek4Ek3;
4→5的过程:
Ek5Ek4;
N-1→N的过程:
EkNEk(N-1)
全过程:
既适用于恒力做功,也适用于变力做功。
N
……
5. 应用动能定理解题的一般步骤:
①确定研究对象。
②通过受力分析、运动分析对物理情景进行分析,画出物体运动的示意图。
③确定研究过程及初末状态,分析该过程中各力做的功及初末状态的动能。
④根据动能定理列方程,然后求解。并对结果进行必要的讨论。
例:一架喷气式飞机,质量m为7.0×104 kg,起飞过程中从静止开始滑跑。当位移l达到2.5×103 m时,速度达到起飞速度80 m/s。在此过程中,飞机受到的平均阻力是飞机所受重力的 。g取10 m/s2,求飞机平均牵引力的大小。
解:以飞机为研究对象
ΔEk
F
mg
FN
kmg
v
l
( F-kmg )
F=1.04×105 N
v0=0
0
资料
l
例:质量为8 g的子弹,以300 m/s的速度射入厚度为5 cm的固定木板(如图所示),射穿后的速度是100 m/s。子弹射穿木板的过程中受到的平均阻力是多大?
f
v
ΔEk
f l
f ×103 N
解:以子弹为研究对象
资料
例:民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面,若斜面高 3.2 m,斜面长6.5 m,质量为60 kg的人沿斜面滑下时所受的阻力是240 N,求人滑至底端时的速度大小,g取10 m/s2。
H
L
v0=0
θ
方法一:牛顿第二定律+运动学规律
mg
FN
f
v=?
例:民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面,若斜面高 3.2 m,斜面长6.5 m,质量为60 kg的人沿斜面滑下时所受的阻力是240 N,求人滑至底端时的速度大小,g取10 m/s2。请用动能定理解答。
H
L
v0=0
θ
方法二:动能定理
mg
FN
f
ΔEk
WG+Wf
mgH f l
0
v=?
解:以人和滑雪板为研究对象
ΔEk
mgh +Wf
0
Wf J
例:哈尔滨第24届世界大学生冬运会某滑雪道为曲线轨道,滑雪道长
s=2.5×103 m,竖直高度h=720 m。运动员从该滑道顶端由静止开始滑下,经t=200s到达滑雪道底端时速度v=30 m/s,人和滑雪板的总质量
m=80 kg,取g=10 m/s2,求人和滑雪板在滑动过程中克服阻力做的功.
mg
FN
人和滑雪板克服阻力做的功为 J
f
资料
例:人们有时用“打夯”的方式把松散的地面夯实(如图所示)。设某次打夯符合以下模型:两人同时通过绳子对重物各施加一个力,力的大小均为320 N,方向都与竖直方向成37°,重物离开地面30 cm后人停止施力,最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg,
g取10 m/s2, cos 37°=0.8。求:
(1)重物刚落地时的速度是多大?
(2)重物对地面的平均冲击力是多大?
分析过程:
① 加速上升( A→B )
H
v0=0
B
A
vB
mg
vA
C
h
vC=0
② 竖直上抛,返回地面( B→A)
③ 减速下降( A→ C)
例:两人同时通过绳子对重物各施加一个力,力的大小均为320 N,方向都与竖直方向成37°,重物离开地面30 cm后人停止施力,最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg, g取10 m/s2, cos 37°=0.8。求:
(1)重物刚落地时的速度是多大?
vA
解:以A→B →A为研究过程
ΔEk
H
v0=0
B
A
vB
mg
T
T
θ
T合
mg
T合H
(2Tcosθ)H
0
例:两人同时通过绳子对重物各施加一个力,力的大小均为320 N,方向都与竖直方向成37°,重物离开地面30 cm后人停止施力,最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg, g取10 m/s2, cos 37°=0.8。求:
以A→C为研究过程
解:
ΔEk
WG+WF
mg
F
mgh Fh
= 0
F=8.18×103 N
H
v0=0
B
A
vB
vA
C
h
vC=0
(2)重物对地面的平均冲击力是多大?
根据牛顿第三定律,重物对地面的平均冲击力大小为8.18×103 N
根据牛顿第三定律,重物对地面的平均冲击力大小为8.18×103 N
例:两人同时通过绳子对重物各施加一个力,力的大小均为320 N,方向都与竖直方向成37°,重物离开地面30 cm后人停止施力,最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg, g取10 m/s2, cos 37°=0.8。求:
mg
F
H
v0=0
B
A
vB
vA
C
h
vC=0
(2)重物对地面的平均冲击力是多大?
对全过程(A→ B→ C)
解法二:
ΔEk
WT +WG+WF
T合H+mgh Fh
F=8.18×103 N
= 0
mg
T
T
θ
T合
mg
课堂小结
动能
动能定理
1. 物体由于运动而具有的能叫做动能
2. 表达式:
3. 国际单位:
焦耳(J)
4. 动能是标量、状态量
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化。
2.表达式:
Ek末Ek初
或
ΔEk
3. 适用范围:
直线、曲线;
恒力、变力。
4. 应用动能定理解决问题。
课后作业:
1. 分析教材第88页第1题、第2题;第100页第2题、第4题。
2. 查阅资料,了解动能定理在解决哪些实际的力学问题中,得到了应用?
山东舰
资料
