16.1 二次根式(实例均为2013中考教师讲解典型题)课件
文档属性
| 名称 | 16.1 二次根式(实例均为2013中考教师讲解典型题)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 829.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-16 00:00:00 | ||
图片预览










文档简介
课件30张PPT。二 次 根 式
1.掌握二次根式的性质.(重点)
2.会用二次根式的性质将简单的二次根式化简.(重点、难点)1.二次根式的性质.
(1) 是__的算术平方根,所以 =__;
是__的算术平方根,所以 =__.
(2) =__, =____, =____, =___.
(3) =__, =____, =____,
=___.
(4) =__.553340.21040.2100【思考】1. (a≥0)的取值范围是多少?
提示: (a≥0)表示非负数a的算术平方根,所以 ≥0.
2.通过对上面(1)中的填空,你能发现 (a≥0)的值等于
多少?
提示: 表示非负数a的算术平方根,
所以 =a(a≥0).3.通过对上面(2)(3)(4)的计算你能发现 的值有什么规
律?
提示:①当a>0时, =a;
②当a=0时, =0;
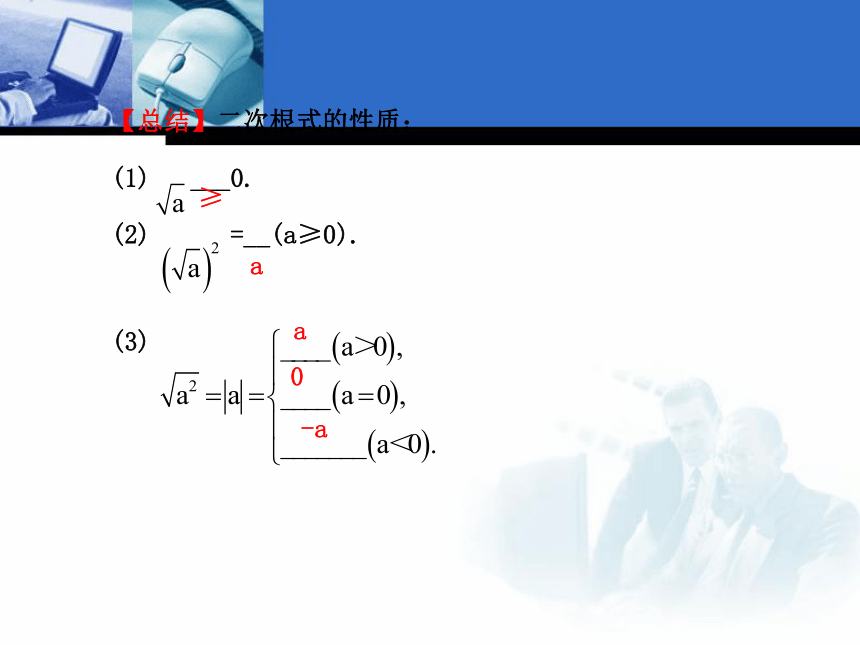
③当a<0时, =-a.【总结】二次根式的性质:
(1) ___0.
(2) =__(a≥0).
(3)≥aa0-a2.代数式.
用基本运算符号(加、减、乘、除、乘方和开方)把___和表示
数的_____连接起来的式子.数字母 (打“√”或“×”)
(1) =15.( )
(2) =-17.( )
(3) =10-2.( )
(4)当a是非负数时, ( )
(5) =±a2.( )√×√√×知识点 1 二次根式的性质
【例1】计算:
【思路点拨】(1)题利用 =a(a≥0)计算.(2)题利用
(ab)2=a2b2及 =a(a≥0)进行计算.(3)题先转化为 的
形式,再利用 =a(a≥0)计算.(4)题利用 =a
(a≥0)计算.【自主解答】(1)
(2)
(3)
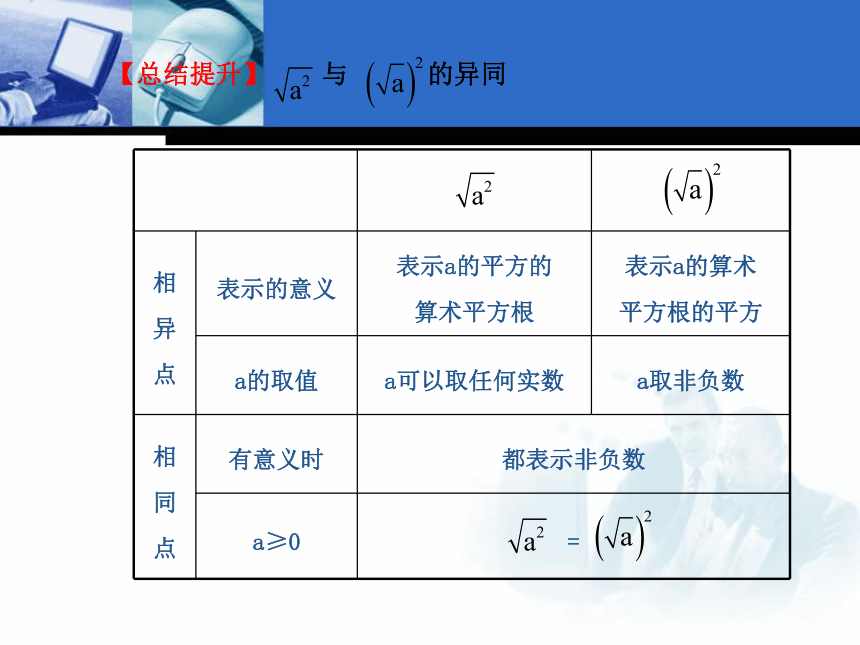
(4)【总结提升】 与 的异同知识点 2 二次根式性质的应用
【例2】(2013·青海中考)已知实数a在数轴上的位置如图所
示,则化简|a-1|+ 的结果是________.【教你解题】【总结提升】利用 =|a|化简时的两点注意
(1)用 =|a|化简时,要注意被开方数中a的符号,当a<0
时, =-a,而不是 =a.
(2)若被开方数是多项式,应先因式分解,再根据条件进行化
简.题组一:二次根式的性质
1.下列各式成立的是( )
【解析】选C.因为 所以选项A不成立;因为
=5,所以选项B不成立;因为 =10, =10,所以
因此,选项C成立;因为
=4×5=20,所以 ≠-20,因此,选项D不成立.2.如果x是任意实数,则 =( )
A.x B.-x C.x2 D.|x|
【解析】选D.∵x是任意实数,①当x>0时, =x;②当x=0
时, =0;③当x<0时, =-x.
∴ =|x|.3.若 那么关于x的说法是( )
A.x=2 B.x≥2
C.x是任意实数 D.x≤2
【解析】选C.∵
x-2与2-x互为相反数,
∴任意实数x都会满足4.(2013·连云港中考)计算: =______.
【解析】利用 =a(a≥0)直接计算: =3.
答案:35.计算: =_______.
【解析】
答案:1.86.计算: =______.
【解析】
答案:7.计算:
【解析】(1)
(2)
(3) =4-π+π-3=1.题组二:二次根式性质的应用
1.若a为任意实数,下列等式中成立的是( )
【解析】选D.当a<0时, 无意义,因此,若a为任意实数,
则 =a不一定成立;当a>0时, 无意义,因此,若a为
任意实数,则 =-a不一定成立;当a<0时, =-a,
因此,若a为任意实数,则 =a不一定成立;因为
=|a|,所以a为任意实数, 一定成立.2.若x,y为实数,且 则 的值为( )
A.-2 B.2 C.±2 D.4
【解析】选B.由非负数的性质得x+2=0,y-2=0,解得x=-2,
y=2,因此,3.若x>2,化简 的结果为( )
A.x-2 B.2-x
C.x+2 D.-2-x
【解析】选A.∵x>2,∴x-2>0.
∴【变式训练】已知 则x的取值范围是_____.
【解析】∵
∴1-2x≥0,解得
答案:4.实数a,b在数轴上的位置如图所示,则 的化简结
果为_______.
【解析】由题图可知a>0,b<0,且|a|<|b|,所以a+b<0,所
以 =-(a+b)+a=-a-b+a=-b.
答案:-b5.已知a,b,c为三角形的三条边,则
=___________.
【解析】∵a,b,c为三角形的三条边,
∴a+b-c>0,b-a-c<0.
∴
=a+b-c-(b-a-c)
=a+b-c-b+a+c=2a.
答案:2a6.当x=______时,代数式 有最小值,其最小值是_____.
【解析】∵
∴ 的最小值为0.
∴4x+5=0,∴
答案: 07.计算:(1)
(2)
(3)
【解析】(1)
(2)
(3)【想一想错在哪?】化简:
提示:应分x<1和x>1两种情况讨论.
1.掌握二次根式的性质.(重点)
2.会用二次根式的性质将简单的二次根式化简.(重点、难点)1.二次根式的性质.
(1) 是__的算术平方根,所以 =__;
是__的算术平方根,所以 =__.
(2) =__, =____, =____, =___.
(3) =__, =____, =____,
=___.
(4) =__.553340.21040.2100【思考】1. (a≥0)的取值范围是多少?
提示: (a≥0)表示非负数a的算术平方根,所以 ≥0.
2.通过对上面(1)中的填空,你能发现 (a≥0)的值等于
多少?
提示: 表示非负数a的算术平方根,
所以 =a(a≥0).3.通过对上面(2)(3)(4)的计算你能发现 的值有什么规
律?
提示:①当a>0时, =a;
②当a=0时, =0;
③当a<0时, =-a.【总结】二次根式的性质:
(1) ___0.
(2) =__(a≥0).
(3)≥aa0-a2.代数式.
用基本运算符号(加、减、乘、除、乘方和开方)把___和表示
数的_____连接起来的式子.数字母 (打“√”或“×”)
(1) =15.( )
(2) =-17.( )
(3) =10-2.( )
(4)当a是非负数时, ( )
(5) =±a2.( )√×√√×知识点 1 二次根式的性质
【例1】计算:
【思路点拨】(1)题利用 =a(a≥0)计算.(2)题利用
(ab)2=a2b2及 =a(a≥0)进行计算.(3)题先转化为 的
形式,再利用 =a(a≥0)计算.(4)题利用 =a
(a≥0)计算.【自主解答】(1)
(2)
(3)
(4)【总结提升】 与 的异同知识点 2 二次根式性质的应用
【例2】(2013·青海中考)已知实数a在数轴上的位置如图所
示,则化简|a-1|+ 的结果是________.【教你解题】【总结提升】利用 =|a|化简时的两点注意
(1)用 =|a|化简时,要注意被开方数中a的符号,当a<0
时, =-a,而不是 =a.
(2)若被开方数是多项式,应先因式分解,再根据条件进行化
简.题组一:二次根式的性质
1.下列各式成立的是( )
【解析】选C.因为 所以选项A不成立;因为
=5,所以选项B不成立;因为 =10, =10,所以
因此,选项C成立;因为
=4×5=20,所以 ≠-20,因此,选项D不成立.2.如果x是任意实数,则 =( )
A.x B.-x C.x2 D.|x|
【解析】选D.∵x是任意实数,①当x>0时, =x;②当x=0
时, =0;③当x<0时, =-x.
∴ =|x|.3.若 那么关于x的说法是( )
A.x=2 B.x≥2
C.x是任意实数 D.x≤2
【解析】选C.∵
x-2与2-x互为相反数,
∴任意实数x都会满足4.(2013·连云港中考)计算: =______.
【解析】利用 =a(a≥0)直接计算: =3.
答案:35.计算: =_______.
【解析】
答案:1.86.计算: =______.
【解析】
答案:7.计算:
【解析】(1)
(2)
(3) =4-π+π-3=1.题组二:二次根式性质的应用
1.若a为任意实数,下列等式中成立的是( )
【解析】选D.当a<0时, 无意义,因此,若a为任意实数,
则 =a不一定成立;当a>0时, 无意义,因此,若a为
任意实数,则 =-a不一定成立;当a<0时, =-a,
因此,若a为任意实数,则 =a不一定成立;因为
=|a|,所以a为任意实数, 一定成立.2.若x,y为实数,且 则 的值为( )
A.-2 B.2 C.±2 D.4
【解析】选B.由非负数的性质得x+2=0,y-2=0,解得x=-2,
y=2,因此,3.若x>2,化简 的结果为( )
A.x-2 B.2-x
C.x+2 D.-2-x
【解析】选A.∵x>2,∴x-2>0.
∴【变式训练】已知 则x的取值范围是_____.
【解析】∵
∴1-2x≥0,解得
答案:4.实数a,b在数轴上的位置如图所示,则 的化简结
果为_______.
【解析】由题图可知a>0,b<0,且|a|<|b|,所以a+b<0,所
以 =-(a+b)+a=-a-b+a=-b.
答案:-b5.已知a,b,c为三角形的三条边,则
=___________.
【解析】∵a,b,c为三角形的三条边,
∴a+b-c>0,b-a-c<0.
∴
=a+b-c-(b-a-c)
=a+b-c-b+a+c=2a.
答案:2a6.当x=______时,代数式 有最小值,其最小值是_____.
【解析】∵
∴ 的最小值为0.
∴4x+5=0,∴
答案: 07.计算:(1)
(2)
(3)
【解析】(1)
(2)
(3)【想一想错在哪?】化简:
提示:应分x<1和x>1两种情况讨论.
