17.1.1 勾股定理(实例均为2013中考教师讲解典型题)课件
文档属性
| 名称 | 17.1.1 勾股定理(实例均为2013中考教师讲解典型题)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 767.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-16 00:00:00 | ||
图片预览










文档简介
课件31张PPT。勾 股 定 理
1.掌握利用勾股定理解决实际问题.(重点)
2.理解立体图形中两点间距离最短问题.(重点、难点)一、利用勾股定理解决实际问题的一般步骤
1.将实际问题转化为数学问题.
2.明确已知条件及结论.
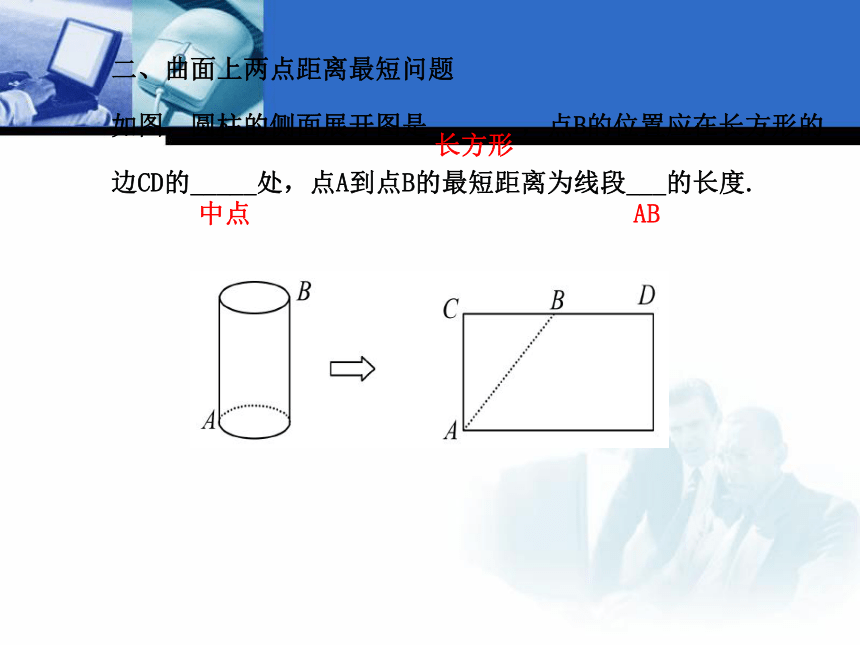
3.利用勾股定理解答,确定实际问题的答案.二、曲面上两点距离最短问题
如图,圆柱的侧面展开图是_______,点B的位置应在长方形的
边CD的_____处,点A到点B的最短距离为线段___的长度.长方形中点AB【思考】1.平面内,两点之间的最短距离怎样确定?
提示:连接两点之间的线段的长度即是.
2.如上图,怎样确定线段AB的长度?
提示:根据勾股定理,即AB2=AC2+BC2.
【总结】解决曲面上两点之间的距离最短问题的思路是:把立
体图形展开为_________,将曲面两点间最短距离问题转化为
平面内_______________问题.平面图形两点间线段长度 (打“√”或“×”)
(1)应用勾股定理的前提是三角形是直角三角形.( )
(2)只用米尺不能确定一个门框的两边是否垂直.( )
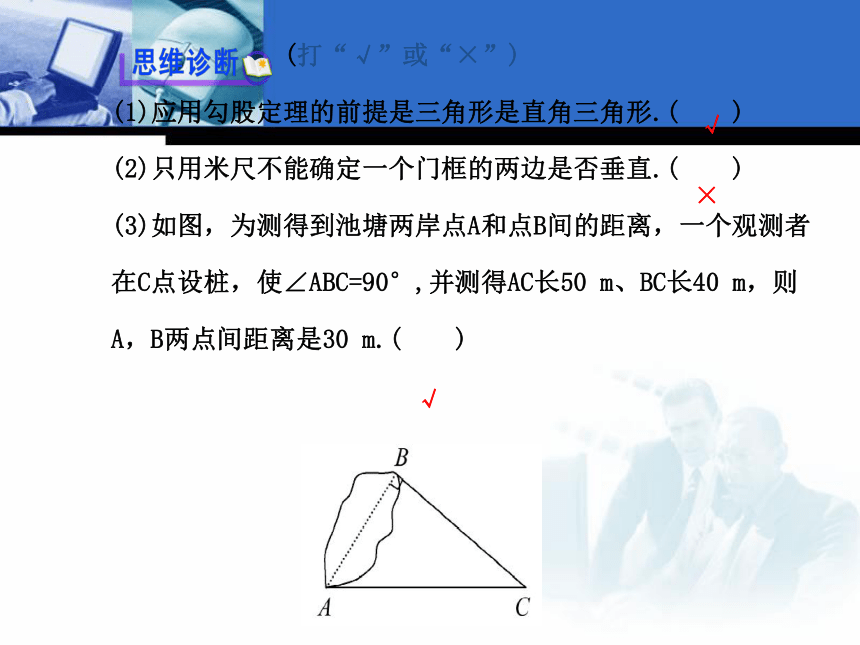
(3)如图,为测得到池塘两岸点A和点B间的距离,一个观测者
在C点设桩,使∠ABC=90°,并测得AC长50 m、BC长40 m,则
A,B两点间距离是30 m.( )√×√知识点 1 勾股定理的实际应用
【例1】如图,在公路AB旁有一座山,
现有一C处需要爆破,已知点C与公路
上的停靠站A距离为300 m,与公路上
另一停靠站B的距离为400 m,且CA⊥CB,为了安全起见,爆破点C周围半径250 m范围内不得进入,问在进行爆破时,公路AB段是否因有危险而需要暂时封锁?【思路点拨】要判断公路AB段是否需要封锁→需要计算点C到AB的距离与250 m的大小关系→借助勾股定理和三角形的面积计算点C到AB的距离.【自主解答】作CD⊥AB于D.
因为BC=400 m,AC=300 m,∠ACB=90°,根据勾股定理,得AC2+BC2=AB2,即3002+4002=AB2,所以AB=500 m.
由三角形的面积可知:
所以500·CD=400×300,
所以CD=240 m.
因为240<250,即点C到AB的距离
小于250 m,
所以有危险,公路AB段需要暂时封锁.【总结提升】应用勾股定理解决实际问题的步骤
(1)读懂题意,建立数学模型.
(2)分析数量关系,数形结合,正确标图,将已知条件体现到图形中,充分利用图形的功能和性质.
(3)应用勾股定理进行计算或建立等量关系,构建方程求解.
(4)解决实际问题.知识点 2 立体图形中最短路径问题
【例2】如图所示,有一个长、宽都是2 m,高
为3 m的长方体纸盒,一只小蚂蚁从A点爬到B点,
那么这只蚂蚁爬行的最短路径为( )
A.3 m B.4 m C.5 m D.6 m
【思路点拨】展开面两种情况→连接AB→勾股定理→计算→比较→答案.【自主解答】选C.展开包含点A,点B的两个面,有两种情况,如图:
分别连接AB,得Rt△ABD,
由勾股定理得图(1)中AB2=(2+2)2+32=25,
图(2)中AB2=22+(3+2)2=29,因为29>25,
所以蚂蚁应沿图(1)展开图中AB爬行,爬行最短路径为5 m,故选C.【总结提升】求立体图形中最短路径问题的“四步法”题组一:勾股定理的实际应用
1.如图,在水塔O的东北方向32 m处有一抽水站A.在水塔的东南方向24 m处有一建筑工地B,若在AB间建一直水管,则水管的长为( )
A.45 m B.40 m C.50 m D.56 m【解析】选B.由题意知△AOB为直角三角形,
因为OA=32 m,OB=24 m,
所以2.在布置新年联欢会的会场时,小虎准备把同学们做的拉花用上,他搬来了一架高为2.5 m的梯子,要想把拉花挂在高2.4 m的墙上,小虎应把梯子的底端放在距离墙______m处.
【解析】由勾股定理得,梯子的底端到墙的距离为
答案:0.73.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200 m,结果他在水中实际游了520 m,则该河流的宽度为_________m.
【解析】由勾股定理得,
答案:4804.如图所示,学校有一块长方形花圃,有极
少数人为了避开拐角走“捷径”,在花圃内
走出了一条“路”.他们仅仅少走了_______
步路(假设2步为1 m),却踩伤了花草.
【解析】根据勾股定理可得斜边长是
则少走的距离是3+4-5=2(m),即4步.
答案:45.小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,求旗杆的高度.【解析】设旗杆的高度AC为x m,
那么绳子的长度AB为(x+1) m,
根据题意得到△ABC为直角三角形,∠C=90°,
根据勾股定理得到:
52+x2=(x+1)2,
解得x=12.
答:旗杆的高度为12 m.6.如图所示,从电线杆离地8 m高的A处向地面B处拉一条长
10 m的缆绳,如果从电线杆离地6 m高的C处同样拉一条长10 m
的缆绳,这条缆绳在地面的固定点D与B点的距离有多远?【解析】在Rt△AEB中,AE=8,AB=10,
由勾股定理得,EB=6;
在Rt△CED中,CE=6,CD=10,由勾股定理得,DE=8,所以DB=DE-BE=8-6=2(m).题组二:立体图形中最短路径问题
1.如图,圆柱的底面周长为12 cm,高AB为4 cm,
BC是直径,一只蚂蚁从点A出发沿着圆柱体的表
面爬行到点C的最短路程大约是( )
A.6 cm B.12 cm
C.12.6 cm D.16 cm【解析】选C.把圆柱沿直径BC剪开成两半,展开成平面后可
得如图所示,则蚂蚁从点A爬行到点C的最短路程是长方形的对
角线AC的长,因为AB=4,BC=12,所以2.如图,长方体的底面边长分别为1 cm和3 cm,
高为6 cm.如果用一根细线从点A开始经过4个侧
面缠绕一圈到达点B,那么所用细线最短需要( )
A.8 cm B.10 cm
C.12 cm D.15 cm
【解析】选B.把长方体的四个侧面展开为一个长方形,这个长方形的长为3+1+3+1=8,宽为6,此时从A到B的最短距离为线段AB.连接AB,由勾股定理可求出AB=10.3.如图,一个正方体盒子的棱长为a cm,顶点C′处有一只昆虫甲,顶点A处有一只昆虫乙.假设昆虫甲在顶点C′处不动,昆虫乙沿盒壁爬行到昆虫甲的位置C′的最短路径的长是________cm.(盒壁的厚度忽略不计)【解析】由题意画出部分平面展开图,如图所示,∵CC′=AB=BC=a cm,
所以AC′=
答案:4.如图所示的圆柱体中底面圆的半径是 高为2,若一只小
虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短
路程是________(结果保留根号).【解析】分两种情况进行计算,再比较哪条线路的长度最
短.(1)以底面圆周长的一半和高BC为直角边,AC为斜边,构建
直角三角形,求得斜边AC的长为 (2)AB为底面圆的直径与
高BC的和是 所以小虫爬行的最短路程是
答案:【想一想错在哪?】如图,王大伯家屋后有一块
长12 m,宽8 m的矩形空地,他在以长边BC为直
径的半圆内种菜,他家养的一只羊平时拴A处的
一棵树上,为了不让羊吃到菜,拴羊的绳长可
以选用( )
A.3 m B.5 m C.7 m D.9 m提示:没正确分析题意,应该利用勾股定理解答.
1.掌握利用勾股定理解决实际问题.(重点)
2.理解立体图形中两点间距离最短问题.(重点、难点)一、利用勾股定理解决实际问题的一般步骤
1.将实际问题转化为数学问题.
2.明确已知条件及结论.
3.利用勾股定理解答,确定实际问题的答案.二、曲面上两点距离最短问题
如图,圆柱的侧面展开图是_______,点B的位置应在长方形的
边CD的_____处,点A到点B的最短距离为线段___的长度.长方形中点AB【思考】1.平面内,两点之间的最短距离怎样确定?
提示:连接两点之间的线段的长度即是.
2.如上图,怎样确定线段AB的长度?
提示:根据勾股定理,即AB2=AC2+BC2.
【总结】解决曲面上两点之间的距离最短问题的思路是:把立
体图形展开为_________,将曲面两点间最短距离问题转化为
平面内_______________问题.平面图形两点间线段长度 (打“√”或“×”)
(1)应用勾股定理的前提是三角形是直角三角形.( )
(2)只用米尺不能确定一个门框的两边是否垂直.( )
(3)如图,为测得到池塘两岸点A和点B间的距离,一个观测者
在C点设桩,使∠ABC=90°,并测得AC长50 m、BC长40 m,则
A,B两点间距离是30 m.( )√×√知识点 1 勾股定理的实际应用
【例1】如图,在公路AB旁有一座山,
现有一C处需要爆破,已知点C与公路
上的停靠站A距离为300 m,与公路上
另一停靠站B的距离为400 m,且CA⊥CB,为了安全起见,爆破点C周围半径250 m范围内不得进入,问在进行爆破时,公路AB段是否因有危险而需要暂时封锁?【思路点拨】要判断公路AB段是否需要封锁→需要计算点C到AB的距离与250 m的大小关系→借助勾股定理和三角形的面积计算点C到AB的距离.【自主解答】作CD⊥AB于D.
因为BC=400 m,AC=300 m,∠ACB=90°,根据勾股定理,得AC2+BC2=AB2,即3002+4002=AB2,所以AB=500 m.
由三角形的面积可知:
所以500·CD=400×300,
所以CD=240 m.
因为240<250,即点C到AB的距离
小于250 m,
所以有危险,公路AB段需要暂时封锁.【总结提升】应用勾股定理解决实际问题的步骤
(1)读懂题意,建立数学模型.
(2)分析数量关系,数形结合,正确标图,将已知条件体现到图形中,充分利用图形的功能和性质.
(3)应用勾股定理进行计算或建立等量关系,构建方程求解.
(4)解决实际问题.知识点 2 立体图形中最短路径问题
【例2】如图所示,有一个长、宽都是2 m,高
为3 m的长方体纸盒,一只小蚂蚁从A点爬到B点,
那么这只蚂蚁爬行的最短路径为( )
A.3 m B.4 m C.5 m D.6 m
【思路点拨】展开面两种情况→连接AB→勾股定理→计算→比较→答案.【自主解答】选C.展开包含点A,点B的两个面,有两种情况,如图:
分别连接AB,得Rt△ABD,
由勾股定理得图(1)中AB2=(2+2)2+32=25,
图(2)中AB2=22+(3+2)2=29,因为29>25,
所以蚂蚁应沿图(1)展开图中AB爬行,爬行最短路径为5 m,故选C.【总结提升】求立体图形中最短路径问题的“四步法”题组一:勾股定理的实际应用
1.如图,在水塔O的东北方向32 m处有一抽水站A.在水塔的东南方向24 m处有一建筑工地B,若在AB间建一直水管,则水管的长为( )
A.45 m B.40 m C.50 m D.56 m【解析】选B.由题意知△AOB为直角三角形,
因为OA=32 m,OB=24 m,
所以2.在布置新年联欢会的会场时,小虎准备把同学们做的拉花用上,他搬来了一架高为2.5 m的梯子,要想把拉花挂在高2.4 m的墙上,小虎应把梯子的底端放在距离墙______m处.
【解析】由勾股定理得,梯子的底端到墙的距离为
答案:0.73.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200 m,结果他在水中实际游了520 m,则该河流的宽度为_________m.
【解析】由勾股定理得,
答案:4804.如图所示,学校有一块长方形花圃,有极
少数人为了避开拐角走“捷径”,在花圃内
走出了一条“路”.他们仅仅少走了_______
步路(假设2步为1 m),却踩伤了花草.
【解析】根据勾股定理可得斜边长是
则少走的距离是3+4-5=2(m),即4步.
答案:45.小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,求旗杆的高度.【解析】设旗杆的高度AC为x m,
那么绳子的长度AB为(x+1) m,
根据题意得到△ABC为直角三角形,∠C=90°,
根据勾股定理得到:
52+x2=(x+1)2,
解得x=12.
答:旗杆的高度为12 m.6.如图所示,从电线杆离地8 m高的A处向地面B处拉一条长
10 m的缆绳,如果从电线杆离地6 m高的C处同样拉一条长10 m
的缆绳,这条缆绳在地面的固定点D与B点的距离有多远?【解析】在Rt△AEB中,AE=8,AB=10,
由勾股定理得,EB=6;
在Rt△CED中,CE=6,CD=10,由勾股定理得,DE=8,所以DB=DE-BE=8-6=2(m).题组二:立体图形中最短路径问题
1.如图,圆柱的底面周长为12 cm,高AB为4 cm,
BC是直径,一只蚂蚁从点A出发沿着圆柱体的表
面爬行到点C的最短路程大约是( )
A.6 cm B.12 cm
C.12.6 cm D.16 cm【解析】选C.把圆柱沿直径BC剪开成两半,展开成平面后可
得如图所示,则蚂蚁从点A爬行到点C的最短路程是长方形的对
角线AC的长,因为AB=4,BC=12,所以2.如图,长方体的底面边长分别为1 cm和3 cm,
高为6 cm.如果用一根细线从点A开始经过4个侧
面缠绕一圈到达点B,那么所用细线最短需要( )
A.8 cm B.10 cm
C.12 cm D.15 cm
【解析】选B.把长方体的四个侧面展开为一个长方形,这个长方形的长为3+1+3+1=8,宽为6,此时从A到B的最短距离为线段AB.连接AB,由勾股定理可求出AB=10.3.如图,一个正方体盒子的棱长为a cm,顶点C′处有一只昆虫甲,顶点A处有一只昆虫乙.假设昆虫甲在顶点C′处不动,昆虫乙沿盒壁爬行到昆虫甲的位置C′的最短路径的长是________cm.(盒壁的厚度忽略不计)【解析】由题意画出部分平面展开图,如图所示,∵CC′=AB=BC=a cm,
所以AC′=
答案:4.如图所示的圆柱体中底面圆的半径是 高为2,若一只小
虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短
路程是________(结果保留根号).【解析】分两种情况进行计算,再比较哪条线路的长度最
短.(1)以底面圆周长的一半和高BC为直角边,AC为斜边,构建
直角三角形,求得斜边AC的长为 (2)AB为底面圆的直径与
高BC的和是 所以小虫爬行的最短路程是
答案:【想一想错在哪?】如图,王大伯家屋后有一块
长12 m,宽8 m的矩形空地,他在以长边BC为直
径的半圆内种菜,他家养的一只羊平时拴A处的
一棵树上,为了不让羊吃到菜,拴羊的绳长可
以选用( )
A.3 m B.5 m C.7 m D.9 m提示:没正确分析题意,应该利用勾股定理解答.
