17.1.2 勾股定理(实例均为2013中考教师讲解典型题)课件
文档属性
| 名称 | 17.1.2 勾股定理(实例均为2013中考教师讲解典型题)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 804.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-16 00:00:00 | ||
图片预览






文档简介
课件29张PPT。勾 股 定 理
1.掌握利用勾股定理在数轴上表示无理数.(重点)
2.会用勾股定理求线段的长.(重点、难点)1.在数轴上表示
要在数轴上画出表示 的点,只要画出长为 的线段即可.
利用勾股定理,长为 的线段是直角边为正整数__,__的直角
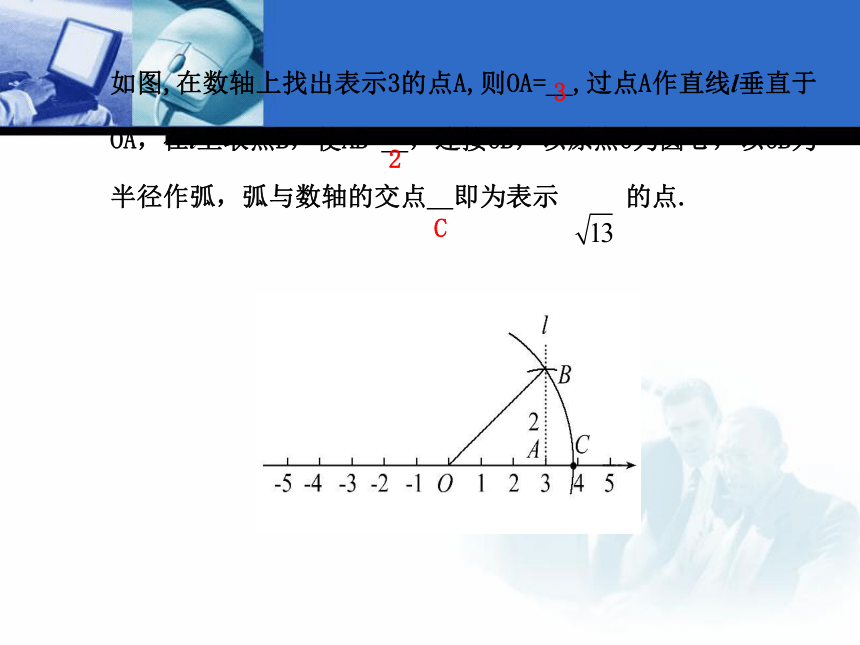
三角形的斜边.23如图,在数轴上找出表示3的点A,则OA=__,过点A作直线l垂直于
OA,在l上取点B,使AB=__,连接OB,以原点O为圆心,以OB为
半径作弧,弧与数轴的交点__即为表示 的点.32C2.作长为 (n为正整数)的线段.
(1)有理数和_______都可以在数轴上表示出来.
(2)当直角三角形的两直角边分别为1,1,斜边长为____,即
当两直角边分别为 1,斜边长为____,即
…,依次可以画出长为 …,的线
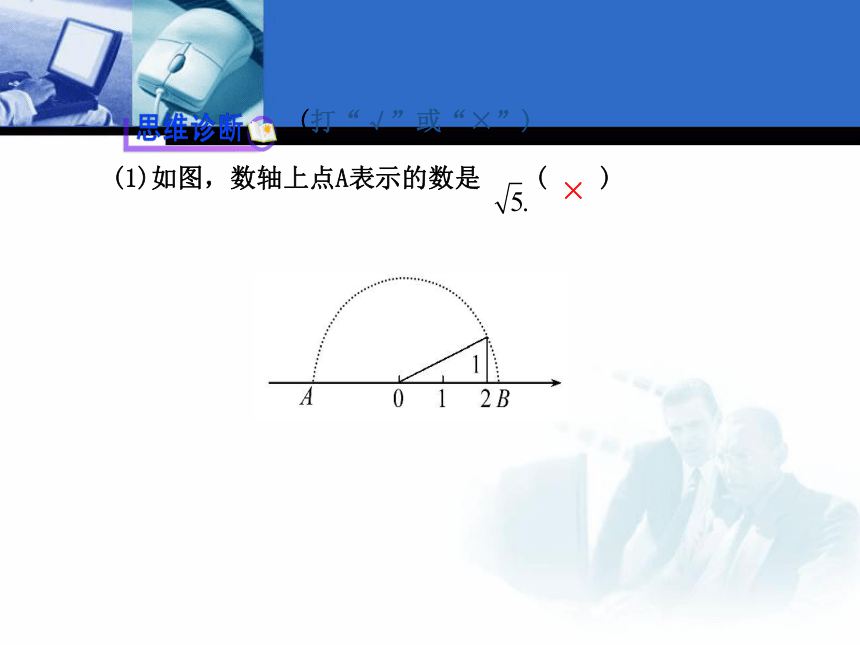
段.无理数 (打“√”或“×”)
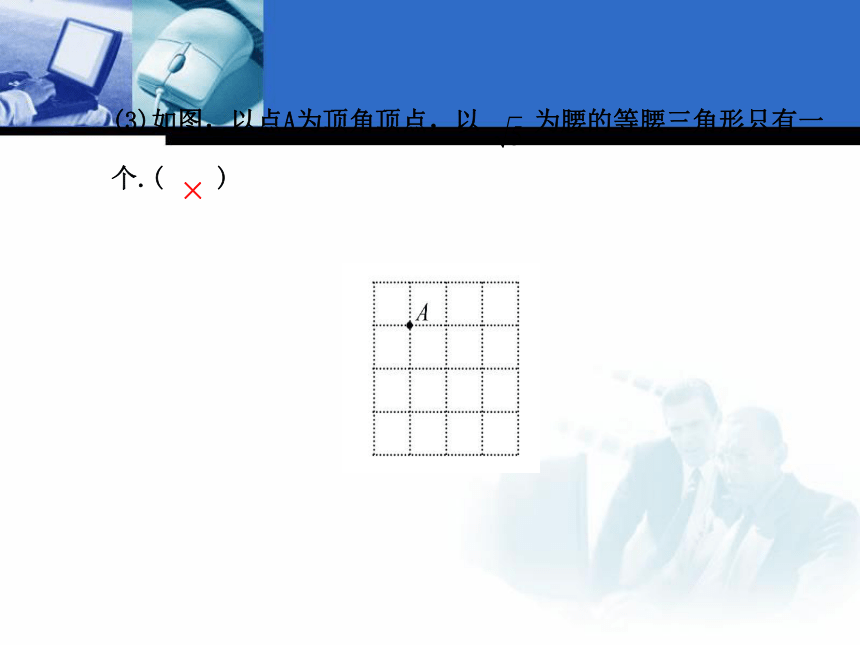
(1)如图,数轴上点A表示的数是 ( )×(2)如图,点A(0,8),AB=10,则点B的坐标是(-6,0).( )√(3)如图,以点A为顶角顶点,以 为腰的等腰三角形只有一
个.( )×知识点 1 在数轴上表示无理数
【例1】在数轴上作出表示 的点.
【思路点拨】根据在数轴上表示无理数的方法→先把 视为
直角三角形斜边的长→确定两条直角边的长度→在数轴上作出.【自主解答】(1)作一个两直角边分别为2,5的直角三角形OAB.
(2)以原点O为圆心,所画直角三角形OAB的斜边OA为半径画
弧,交数轴的正半轴于一点C,点C就是所求的表示 的点.【总结提升】在数轴上表示无理数的三步法
一“拆分”:利用勾股定理拆分出哪两条线段长的平方和等于所画线段(斜边)长的平方.
二“构造”:以数轴原点为直角三角形斜边的顶点,构造直角三角形.
三“画弧”:以数轴原点为圆心,以斜边长为半径画弧,即可在数轴上找到表示该无理数的点.知识点 2 勾股定理在网格中的应用
【例2】如图所示,在一个有4×4个小正方
形组成的正方形网格中,阴影部分的面积
与正方形ABCD的面积比是( )
A.3∶4 B.9∶16
C.5∶8 D.1∶2
【思路点拨】设每一个小正方形的边长为1→大正方形的面积→根据勾股定理确定阴影部分正方形的边长及面积.【自主解答】选C.设每一个小正方形的边长为1,则正方形
ABCD的面积就是4×4=16,阴影部分正方形的边长应该是直角
三角形DEF的斜边,另外两条直角边长度分别是1和3,根据勾
股定理可以求出 所以阴影部分正方形的面积就是
所以阴影部分的面积与正方形ABCD的面积比是
10∶16=5∶8.【总结提升】网格中的勾股定理
正方形网格中的每一个角都是直角,所以在正方形网格中的计算都可以归结为求任意两个格点之间的长度问题,一般情况下都是应用勾股定理来进行计算,关键是确定每一条边所在的直角三角形.题组一:在数轴上表示无理数
1.如图,矩形OABC的边OA长为2 ,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )【解析】选D.由勾股定理求出 根据同弧的半径相
等,得这个点表示的实数是2.如图所示,点P是第一象限的角平分线上一点,且OP=2,则点P的坐标为( )【解析】选B.过点P作PA⊥x轴,垂足为点A,由题意得△OPA为
等腰直角三角形,所以OA=PA,根据勾股定理得,OA2+PA2=
OP2,解得OA=PA= 点P在第一象限,故选B.3.(2013·漳州中考)如图,正方形ODBC
中,OC=1,OA=OB,则数轴上点A表示的
数是_________.
【解析】∵OC=1, ∴ ∵OA=OB,
∴数轴上点A表示的数是
答案:4.在数轴上作出表示 的点.
【解析】在数轴上作一个两直角边分别为2,1的直角三角形;
以原点为圆心,所画直角边的斜边为半径画弧,交数轴的负半
轴于一点A,这点就是所求的表示 的点.题组二:勾股定理在网格中的应用
1.如图所示的正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )
A.0 B.1 C.2 D.3【解析】选D.观察图形,应用勾股定理,得AB2=29,
BC2=13,AC2=34,所以三边长都是无理数.2.如图,在6×6的网格(小正方形的边长为1)
中有一个三角形ABC,则三角形ABC的周长是
________(精确到0.001).
【解析】根据题意,得AC=2,BC=3.根据勾股定理得
则三角形的周长是
答案:8.6063.如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是___________.【解析】如图,根据正方形的性质知面积①=面积②,面积③=
面积④,从而得△ABC的面积为一个半正方形的面积即 由勾
股定理可得 ∴BC边上的高是
答案:4.(2013·铜仁中考)如图,已知∠AOB=45°,A1,A2,A3,…,An
在射线OA上,B1,B2,B3,…,Bn在射线OB上,且A1B1⊥OA,
A2B2⊥OA,…,AnBn⊥OA;A2B1⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,
6…),若OA1=1,则A6B6的长是__________.【解析】∠AOB=45°,OA1=1,且A1B1⊥OA,A2B2⊥OA,
∴A1B1=OA1=1,A2B1= 可求A2B2=2,A3B2= A3B3=4=22,
A4B3= …,A6B6=25=32.
答案:32【想一想错在哪?】如图所示,甲船以每小时航行16 n mile的速度离开港口,向东南航行,乙船在同时同地向西南航行,已知它们离开港口一个半小时后分别到达B,A处,且相距
30 n mile,问乙船每小时航行多少n mile?提示:本题错在没有说明三角形是直角三角形.
1.掌握利用勾股定理在数轴上表示无理数.(重点)
2.会用勾股定理求线段的长.(重点、难点)1.在数轴上表示
要在数轴上画出表示 的点,只要画出长为 的线段即可.
利用勾股定理,长为 的线段是直角边为正整数__,__的直角
三角形的斜边.23如图,在数轴上找出表示3的点A,则OA=__,过点A作直线l垂直于
OA,在l上取点B,使AB=__,连接OB,以原点O为圆心,以OB为
半径作弧,弧与数轴的交点__即为表示 的点.32C2.作长为 (n为正整数)的线段.
(1)有理数和_______都可以在数轴上表示出来.
(2)当直角三角形的两直角边分别为1,1,斜边长为____,即
当两直角边分别为 1,斜边长为____,即
…,依次可以画出长为 …,的线
段.无理数 (打“√”或“×”)
(1)如图,数轴上点A表示的数是 ( )×(2)如图,点A(0,8),AB=10,则点B的坐标是(-6,0).( )√(3)如图,以点A为顶角顶点,以 为腰的等腰三角形只有一
个.( )×知识点 1 在数轴上表示无理数
【例1】在数轴上作出表示 的点.
【思路点拨】根据在数轴上表示无理数的方法→先把 视为
直角三角形斜边的长→确定两条直角边的长度→在数轴上作出.【自主解答】(1)作一个两直角边分别为2,5的直角三角形OAB.
(2)以原点O为圆心,所画直角三角形OAB的斜边OA为半径画
弧,交数轴的正半轴于一点C,点C就是所求的表示 的点.【总结提升】在数轴上表示无理数的三步法
一“拆分”:利用勾股定理拆分出哪两条线段长的平方和等于所画线段(斜边)长的平方.
二“构造”:以数轴原点为直角三角形斜边的顶点,构造直角三角形.
三“画弧”:以数轴原点为圆心,以斜边长为半径画弧,即可在数轴上找到表示该无理数的点.知识点 2 勾股定理在网格中的应用
【例2】如图所示,在一个有4×4个小正方
形组成的正方形网格中,阴影部分的面积
与正方形ABCD的面积比是( )
A.3∶4 B.9∶16
C.5∶8 D.1∶2
【思路点拨】设每一个小正方形的边长为1→大正方形的面积→根据勾股定理确定阴影部分正方形的边长及面积.【自主解答】选C.设每一个小正方形的边长为1,则正方形
ABCD的面积就是4×4=16,阴影部分正方形的边长应该是直角
三角形DEF的斜边,另外两条直角边长度分别是1和3,根据勾
股定理可以求出 所以阴影部分正方形的面积就是
所以阴影部分的面积与正方形ABCD的面积比是
10∶16=5∶8.【总结提升】网格中的勾股定理
正方形网格中的每一个角都是直角,所以在正方形网格中的计算都可以归结为求任意两个格点之间的长度问题,一般情况下都是应用勾股定理来进行计算,关键是确定每一条边所在的直角三角形.题组一:在数轴上表示无理数
1.如图,矩形OABC的边OA长为2 ,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )【解析】选D.由勾股定理求出 根据同弧的半径相
等,得这个点表示的实数是2.如图所示,点P是第一象限的角平分线上一点,且OP=2,则点P的坐标为( )【解析】选B.过点P作PA⊥x轴,垂足为点A,由题意得△OPA为
等腰直角三角形,所以OA=PA,根据勾股定理得,OA2+PA2=
OP2,解得OA=PA= 点P在第一象限,故选B.3.(2013·漳州中考)如图,正方形ODBC
中,OC=1,OA=OB,则数轴上点A表示的
数是_________.
【解析】∵OC=1, ∴ ∵OA=OB,
∴数轴上点A表示的数是
答案:4.在数轴上作出表示 的点.
【解析】在数轴上作一个两直角边分别为2,1的直角三角形;
以原点为圆心,所画直角边的斜边为半径画弧,交数轴的负半
轴于一点A,这点就是所求的表示 的点.题组二:勾股定理在网格中的应用
1.如图所示的正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )
A.0 B.1 C.2 D.3【解析】选D.观察图形,应用勾股定理,得AB2=29,
BC2=13,AC2=34,所以三边长都是无理数.2.如图,在6×6的网格(小正方形的边长为1)
中有一个三角形ABC,则三角形ABC的周长是
________(精确到0.001).
【解析】根据题意,得AC=2,BC=3.根据勾股定理得
则三角形的周长是
答案:8.6063.如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是___________.【解析】如图,根据正方形的性质知面积①=面积②,面积③=
面积④,从而得△ABC的面积为一个半正方形的面积即 由勾
股定理可得 ∴BC边上的高是
答案:4.(2013·铜仁中考)如图,已知∠AOB=45°,A1,A2,A3,…,An
在射线OA上,B1,B2,B3,…,Bn在射线OB上,且A1B1⊥OA,
A2B2⊥OA,…,AnBn⊥OA;A2B1⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,
6…),若OA1=1,则A6B6的长是__________.【解析】∠AOB=45°,OA1=1,且A1B1⊥OA,A2B2⊥OA,
∴A1B1=OA1=1,A2B1= 可求A2B2=2,A3B2= A3B3=4=22,
A4B3= …,A6B6=25=32.
答案:32【想一想错在哪?】如图所示,甲船以每小时航行16 n mile的速度离开港口,向东南航行,乙船在同时同地向西南航行,已知它们离开港口一个半小时后分别到达B,A处,且相距
30 n mile,问乙船每小时航行多少n mile?提示:本题错在没有说明三角形是直角三角形.
