18.1.2 平行四边形的判定(实例均为2013中考教师讲解典型题)课件
文档属性
| 名称 | 18.1.2 平行四边形的判定(实例均为2013中考教师讲解典型题)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 696.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-16 23:34:01 | ||
图片预览








文档简介
课件27张PPT。平行四边形的判定
(第2课时) 1.掌握三角形的中位线定理.(重点)
2.会应用三角形的中位线定理进行计算或证明.(重点、难点)1.三角形的中位线的定义:连接三角形两边_____的线段.
2.三角形中位线定理的证明:
如图,DE是△ABC的中位线,求证:DE∥BC,中点证明:如图,延长DE到点F,使EF=DE,连接FC,
在△ADE和△CFE中,
∴△ADE≌△CFE(____),
∴AD=CF,DE=FE,∠ADE=∠F,
∴AD∥CF,DE=SAS又∵AD=DB,∴DB FC,
∴四边形DBCF是___________,
∴DE∥___,DE= DF=_____.平行四边形BC【总结】三角形的中位线定理:
(1)位置关系:三角形的中位线_______第三边.
(2)数量关系:三角形的中位线等于第三边的_____.平行于一半 (打“√”或“×”)
(1)三角形的中位线是直线.( )
(2)一个三角形只有一条中位线.( )
(3)一个三角形的周长是36,则以这个三角形各边中点为顶点
的三角形的周长是18.( )
(4)DE是△ABC的中位线,如果DE=2,那么BC=4.( )××√×知识点 1 三角形的中位线定理
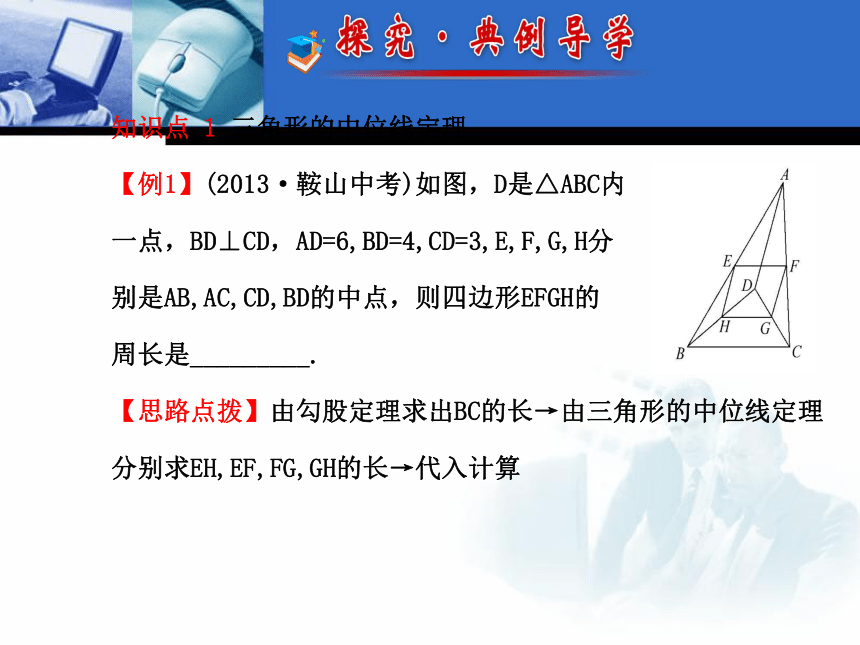
【例1】(2013·鞍山中考)如图,D是△ABC内
一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分
别是AB,AC,CD,BD的中点,则四边形EFGH的
周长是_________.
【思路点拨】由勾股定理求出BC的长→由三角形的中位线定理分别求EH,EF,FG,GH的长→代入计算【自主解答】∵BD⊥CD,BD=4,CD=3,
∴
∵E,F,G,H分别是AB,AC,CD,BD的中点,
∴
∴四边形EFGH的周长为EH+GH+FG+EF=AD+BC,又∵AD=6,BC=5,
∴四边形EFGH的周长为6+5=11.
答案:11【总结提升】三角形的中位线定理的两个结论及四个应用
(1)两个结论:
①中位线与第三边的位置关系——互相平行.
②中位线与第三边的数量关系——中位线等于第三边的一半.
(2)四个应用:
①求线段的长度.
②证明线段相等或平行.
③求角的度数.
④证明线段的倍分关系.知识点 2 三角形中位线定理的实际应用
【例2】(2013·宿迁中考)如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=20 m,则A,B之间的距离是________m.【思路点拨】由C,D分别是边OA,OB的中点,首先判定CD是△AOB的中位线,然后根据三角形的中位线定理,由CD的长,求出A,B之间的距离.
【自主解答】∵C,D分别是OA,OB的中点,
∴CD是△AOB的中位线.
∴AB=2CD=2×20=40 m.
∴A,B之间的距离是40 m.
答案:40【总结提升】三角形的中位线的实际应用
三角形中位线的有关知识,常用来解决以测量距离为背景的题目,解题时常先把实际问题转化为数学问题,再分两步走:一定(依照三角形中位线定义,确定哪条线段是三角形的中位线);二算(根据三角形中位线的性质定理,利用三角形的第三边是三角形中位线的2倍进行计算).题组一:三角形的中位线定理
1.(2013·昆明中考)如图,在△ABC中,
点D,E分别是AB,AC的中点,∠A=50°,
∠ADE=60°,则∠C的度数为( )
A.50° B.60°
C.70° D.80°【解析】选C.由题意得∠AED=180°-∠A-∠ADE=70°,∵点D,E分别是AB,AC的中点,∴DE是△ABC的中位线,∴DE∥BC,∴∠C=∠AED=70°.2.(2013·铜仁中考)已知△ABC的各边长度分别为3 cm,4 cm,
5 cm,则连接各边中点的三角形的周长为( )
A.2 cm B.7 cm C.5 cm D.6 cm
【解析】选D.由三角形的中位线定理可知,连接各边中点的三
角形的周长为 ×(3+4+5)=6 cm.【归纳整合】三角形三条中位线的性质
(1)任何一个三角形都有三条中位线.
(2)三条中位线围成的三角形,其周长是原三角形周长的一半,面积为原三角形面积的四分之一.
(3)三条中位线把原三角形分割成4个全等的小三角形,在原三角形中形成三个面积相等的平行四边形.3.如图,在?ABCD中,AB=10,BC=6,E,F分别是AD,DC的中点,若EF=7,则四边形EACF的周长是( )
A.20 B.22 C.29 D.31
【解析】选C.由已知得AE=3,CF=5,AC=2EF=14,
故四边形EACF的周长是29.4.(2013·邵阳中考)如图所示,在△ABC中,
点D,E分别是AB,AC的中点,连接DE,若
DE=5,则BC=_______.
【解析】∵在△ABC中,点D,E分别是AB,AC的中点,∴
∵DE=5,∴BC=10.
答案:105.已知,如图,在△ABC中,CF平分∠ACB,
CA=CD,AE=EB,
求证:
【证明】∵CA=CD,
CF平分∠ACB,∴AF=DF,
∵AE=EB,∴EF为△ABD的中位线,∴题组二:三角形中位线定理的实际应用
1.如图,是屋架设计图的一部分,点D
是斜梁AB的中点,立柱BC,DE垂直于
横梁AC,AB=8 m,∠A=30°,则DE等
于( )
A.1 m B.2 m C.3 m D.4 m【解析】选B.∵点D是斜梁AB的中点,立柱BC,DE垂直于横梁
AC,∴点E是AC的中点,
∴DE是直角三角形ABC的中位线,
根据三角形的中位线定理得:
又∵在Rt△ABC中,∠A=30°,
∴
故2.如图所示,吴伯伯家一块等边三角形的
空地ABC,已知点E,F分别是边AB,AC的
中点,量得EF=5 m,他想把四边形BCFE用
篱笆围成一圈放养小鸡,则需要篱笆的长
是( )
A.15 m B.20 m C.25 m D.30 m【解析】选C.∵点E,F分别是边AB,AC的中点,EF=5 m,∴BC=2EF=10 m,
∵△ABC是等边三角形,∴AB=BC=AC,
∴
∴篱笆的长为BE+BC+CF+EF
=5+10+5+5=25(m).3.厨房角柜的台面是三角形,如图,如果
把各边中点的连线所围成的三角形铺上黑
色大理石(图中阴影部分).其余部分铺上
白色大理石,那么黑色大理石的面积与白
色大理石面积的比是( )【解析】选C.如图,∵D,E,F分别是AB,BC,AC的中点,
∴DF=BE=EC,EF=AD=BD,DE=AF=FC,∴△BDE≌
△DAF≌△EFC≌△FED,
∴S△BDE=S△DAF=S△EFC=S△FED.
∴黑色大理石的面积与白色大理石面积的比是1∶3.
故选C.【想一想错在哪?】在Rt△ABC中,AC=5,BC=12,D为AC的中点,E为BC的中点,则DE的长为__________.
提示:题目中没有说明哪个角为直角,AB的值应该有两种可能.
(第2课时) 1.掌握三角形的中位线定理.(重点)
2.会应用三角形的中位线定理进行计算或证明.(重点、难点)1.三角形的中位线的定义:连接三角形两边_____的线段.
2.三角形中位线定理的证明:
如图,DE是△ABC的中位线,求证:DE∥BC,中点证明:如图,延长DE到点F,使EF=DE,连接FC,
在△ADE和△CFE中,
∴△ADE≌△CFE(____),
∴AD=CF,DE=FE,∠ADE=∠F,
∴AD∥CF,DE=SAS又∵AD=DB,∴DB FC,
∴四边形DBCF是___________,
∴DE∥___,DE= DF=_____.平行四边形BC【总结】三角形的中位线定理:
(1)位置关系:三角形的中位线_______第三边.
(2)数量关系:三角形的中位线等于第三边的_____.平行于一半 (打“√”或“×”)
(1)三角形的中位线是直线.( )
(2)一个三角形只有一条中位线.( )
(3)一个三角形的周长是36,则以这个三角形各边中点为顶点
的三角形的周长是18.( )
(4)DE是△ABC的中位线,如果DE=2,那么BC=4.( )××√×知识点 1 三角形的中位线定理
【例1】(2013·鞍山中考)如图,D是△ABC内
一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分
别是AB,AC,CD,BD的中点,则四边形EFGH的
周长是_________.
【思路点拨】由勾股定理求出BC的长→由三角形的中位线定理分别求EH,EF,FG,GH的长→代入计算【自主解答】∵BD⊥CD,BD=4,CD=3,
∴
∵E,F,G,H分别是AB,AC,CD,BD的中点,
∴
∴四边形EFGH的周长为EH+GH+FG+EF=AD+BC,又∵AD=6,BC=5,
∴四边形EFGH的周长为6+5=11.
答案:11【总结提升】三角形的中位线定理的两个结论及四个应用
(1)两个结论:
①中位线与第三边的位置关系——互相平行.
②中位线与第三边的数量关系——中位线等于第三边的一半.
(2)四个应用:
①求线段的长度.
②证明线段相等或平行.
③求角的度数.
④证明线段的倍分关系.知识点 2 三角形中位线定理的实际应用
【例2】(2013·宿迁中考)如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=20 m,则A,B之间的距离是________m.【思路点拨】由C,D分别是边OA,OB的中点,首先判定CD是△AOB的中位线,然后根据三角形的中位线定理,由CD的长,求出A,B之间的距离.
【自主解答】∵C,D分别是OA,OB的中点,
∴CD是△AOB的中位线.
∴AB=2CD=2×20=40 m.
∴A,B之间的距离是40 m.
答案:40【总结提升】三角形的中位线的实际应用
三角形中位线的有关知识,常用来解决以测量距离为背景的题目,解题时常先把实际问题转化为数学问题,再分两步走:一定(依照三角形中位线定义,确定哪条线段是三角形的中位线);二算(根据三角形中位线的性质定理,利用三角形的第三边是三角形中位线的2倍进行计算).题组一:三角形的中位线定理
1.(2013·昆明中考)如图,在△ABC中,
点D,E分别是AB,AC的中点,∠A=50°,
∠ADE=60°,则∠C的度数为( )
A.50° B.60°
C.70° D.80°【解析】选C.由题意得∠AED=180°-∠A-∠ADE=70°,∵点D,E分别是AB,AC的中点,∴DE是△ABC的中位线,∴DE∥BC,∴∠C=∠AED=70°.2.(2013·铜仁中考)已知△ABC的各边长度分别为3 cm,4 cm,
5 cm,则连接各边中点的三角形的周长为( )
A.2 cm B.7 cm C.5 cm D.6 cm
【解析】选D.由三角形的中位线定理可知,连接各边中点的三
角形的周长为 ×(3+4+5)=6 cm.【归纳整合】三角形三条中位线的性质
(1)任何一个三角形都有三条中位线.
(2)三条中位线围成的三角形,其周长是原三角形周长的一半,面积为原三角形面积的四分之一.
(3)三条中位线把原三角形分割成4个全等的小三角形,在原三角形中形成三个面积相等的平行四边形.3.如图,在?ABCD中,AB=10,BC=6,E,F分别是AD,DC的中点,若EF=7,则四边形EACF的周长是( )
A.20 B.22 C.29 D.31
【解析】选C.由已知得AE=3,CF=5,AC=2EF=14,
故四边形EACF的周长是29.4.(2013·邵阳中考)如图所示,在△ABC中,
点D,E分别是AB,AC的中点,连接DE,若
DE=5,则BC=_______.
【解析】∵在△ABC中,点D,E分别是AB,AC的中点,∴
∵DE=5,∴BC=10.
答案:105.已知,如图,在△ABC中,CF平分∠ACB,
CA=CD,AE=EB,
求证:
【证明】∵CA=CD,
CF平分∠ACB,∴AF=DF,
∵AE=EB,∴EF为△ABD的中位线,∴题组二:三角形中位线定理的实际应用
1.如图,是屋架设计图的一部分,点D
是斜梁AB的中点,立柱BC,DE垂直于
横梁AC,AB=8 m,∠A=30°,则DE等
于( )
A.1 m B.2 m C.3 m D.4 m【解析】选B.∵点D是斜梁AB的中点,立柱BC,DE垂直于横梁
AC,∴点E是AC的中点,
∴DE是直角三角形ABC的中位线,
根据三角形的中位线定理得:
又∵在Rt△ABC中,∠A=30°,
∴
故2.如图所示,吴伯伯家一块等边三角形的
空地ABC,已知点E,F分别是边AB,AC的
中点,量得EF=5 m,他想把四边形BCFE用
篱笆围成一圈放养小鸡,则需要篱笆的长
是( )
A.15 m B.20 m C.25 m D.30 m【解析】选C.∵点E,F分别是边AB,AC的中点,EF=5 m,∴BC=2EF=10 m,
∵△ABC是等边三角形,∴AB=BC=AC,
∴
∴篱笆的长为BE+BC+CF+EF
=5+10+5+5=25(m).3.厨房角柜的台面是三角形,如图,如果
把各边中点的连线所围成的三角形铺上黑
色大理石(图中阴影部分).其余部分铺上
白色大理石,那么黑色大理石的面积与白
色大理石面积的比是( )【解析】选C.如图,∵D,E,F分别是AB,BC,AC的中点,
∴DF=BE=EC,EF=AD=BD,DE=AF=FC,∴△BDE≌
△DAF≌△EFC≌△FED,
∴S△BDE=S△DAF=S△EFC=S△FED.
∴黑色大理石的面积与白色大理石面积的比是1∶3.
故选C.【想一想错在哪?】在Rt△ABC中,AC=5,BC=12,D为AC的中点,E为BC的中点,则DE的长为__________.
提示:题目中没有说明哪个角为直角,AB的值应该有两种可能.
