18.1.1 平行四边形的性质(实例均为2013中考教师讲解典型题)课件
文档属性
| 名称 | 18.1.1 平行四边形的性质(实例均为2013中考教师讲解典型题)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 708.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-16 23:40:42 | ||
图片预览







文档简介
课件25张PPT。平行四边形的性质
1.掌握平行四边形的对角线互相平分.(重点)
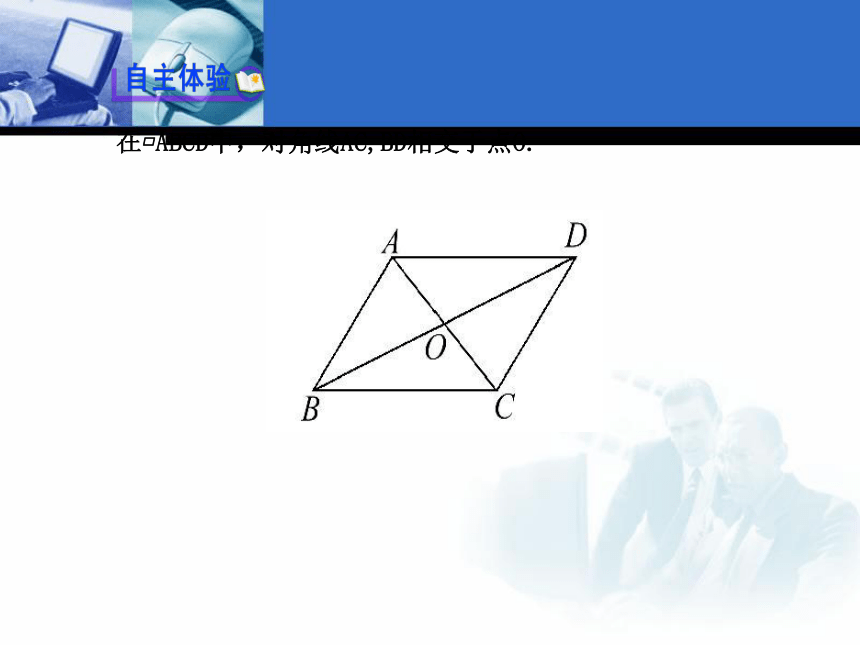
2.熟练应用平行四边形的性质进行计算或证明.(重点、难点)在?ABCD中,对角线AC,BD相交于点O.【思考】
1.平行四边形有哪些性质?
提示:平行四边形的对边相等,对角相等.
2.结合平行四边形的性质,你能判断△ABO与△CDO有怎样的关
系吗?
提示:全等.
3.由此可以得到哪些相等的线段?
提示:OA=OC,OB=OD.
【总结】平行四边形的性质:平行四边形的对角线_________.互相平分 (打“√”或“×”)
(1)平行四边形的对角线相等.( )
(2)平行四边形的对角线把平行四边形分成4个全等的三角
形.( )
(3)平行四边形的对角线平分一组对角.( )×××知识点 1 平行四边形的对角线互相平分
【例1】(2013·南充中考)如图,在?ABCD中,
对角线AC,BD交于点O,经过点O的直线交AB
于点E,交CD于点F.
求证:OE=OF.
【思路点拨】四边形ABCD是平行四边形→AO=CO,AB∥CD→△AOE≌△COF→OE=OF【自主解答】∵四边形ABCD是平行四边形,
∴AO=CO , AB∥CD,∴∠EAO=∠FCO,
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴OE=OF.
【总结提升】平行四边形性质的应用知识点 2 平行四边形性质的综合运用
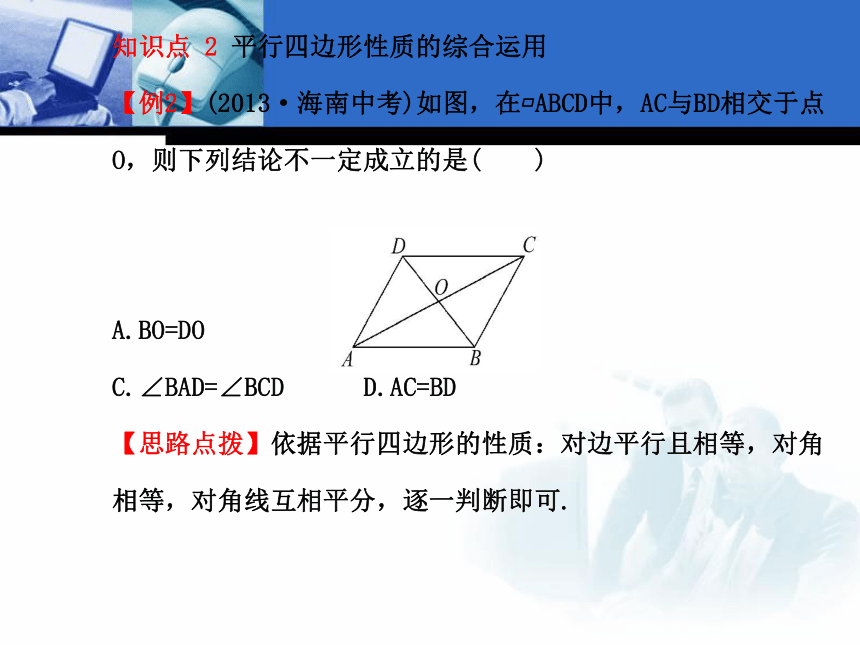
【例2】(2013·海南中考)如图,在?ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )
A.BO=DO B.CD=AB
C.∠BAD=∠BCD D.AC=BD
【思路点拨】依据平行四边形的性质:对边平行且相等,对角相等,对角线互相平分,逐一判断即可.【自主解答】选D.根据平行四边形的对角线互相平分,可得BO=DO,选项A正确;根据平行四边形的对边相等,可得CD=AB,选项B正确;根据平行四边形的对角相等,可得∠BAD=∠BCD,选项C正确;而选项D中“AC=BD”说明对角线相等,平行四边形没有这一性质,因此选项D错误;故选D.【总结提升】平行四边形性质的综合运用
研究平行四边形的性质往往从边、角、对角线3个方面考虑:①边:平行四边形的对边平行且相等.②角:平行四边形的对角相等、邻角互补.③对角线:平行四边形的对角线互相平分.题组一:平行四边形的对角线互相平分
1.如图所示,在?ABCD中,对角线AC,BD交于点O,下列式子中一定成立的是( )
A.AO=OD B.OA=OC C.∠AOD=120° D.∠DOC=45°
【解析】选B.根据平行四边形的对角线互相平分可知一定成立的是选项B.2.如图所示,在平行四边形ABCD中,O为对角
线AC,BD的交点,与△AOD全等的是( )
A.△ABC B.△ADC
C.△BCD D.△COB
【解析】选D.∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,AD=BC,
∴△AOD≌△COB(ASA).3.如图,在平行四边形ABCD中,AC,BD为
对角线,BC=6,BC边上的高为4,则图中
阴影部分的面积为( )
A.3 B.6 C.12 D.24
【解析】选C.由于在平行四边形中,对边分别平行且相等,
对角线互相平分,图中的线段把平行四边形分成5组全等三角
形,通过仔细观察分析图中阴影部分,可得出每组全等三角形
中有一个带阴影,所以阴影部分的面积是平行四边形面积的一
半.所以S阴影= ×6×4=12.4.若点O为?ABCD的对角线AC与BD的交点,且AO+BO=11 cm,则AC+BD=_______cm.
【解析】∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴AC=2AO,BD=2BO,
∴AC+BD=2(AO+BO)=22 cm.
答案:225.如图,在四边形ABCD中,AB∥CD,
AD∥BC,AC,BD相交于点O.若AC=6,
则线段AO的长度等于_________.
【解析】∵在四边形ABCD中,AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵AC=6,
∴AO=
答案:36.如图所示,平行四边形ABCD的周长是18 cm,对角线AC,BD相交于点O,若△AOD与△AOB的周长差是5 cm,则边AB的长是_______cm.【解析】∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵△AOD的周长=OA+OD+AD,
△AOB的周长=OA+OB+AB,
又∵△AOD与△AOB的周长差是5 cm,
∴AD=AB+5,设AB=x,AD=5+x,
则2(x+5+x)=18,解得x=2,即AB=2 cm.
答案:27.如图,?ABCD和?EAFC的顶点D,B,E,F在同一条直线上.求证:DE=BF.
【证明】连接AC,交BD于O.
则OB=OD,OE=OF,
∴OD-OE=OB-OF,即DE=BF.题组二:平行四边形性质的综合运用
1.(2013·云南中考)如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论正确的是( )
A.S?ABCD=4S△AOB
B.AC=BD
C.AC⊥BD
D.平行四边形ABCD是轴对称图形【解析】选A.平行四边形两条对角线把它分成的四个三角形有两对全等三角形,但是这四个三角形的面积都是相等的,因为△AOD与△AOB是等底等高的,A正确;平行四边形的对角线互相平分,但不一定相等也不一定垂直,所以B,C错误;对于平行四边形不一定能找到一条直线,沿此直线折叠,使直线两旁的部分完全重合,所以它不一定是轴对称图形,D错误.故选A. 2.如图所示,?ABCD中,两条对角线AC,
BD相交于点O,AF⊥BD于F,CE⊥BD于E,
则图中全等三角形的对数共有( )
A.5对 B.6对 C.7对 D.8对
【解析】选C.∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OA=OC,OB=OD.
∴△ABD≌△CDB,△ACD≌△CAB,△AOB≌△COD,△AOD≌△COB.
∵AF⊥BD于F,CE⊥BD于E,
∴△ABF≌△CDE,△AFD≌△CEB,△AOF≌△COE.3.如图所示,在?ABCD中,E,F是对角线AC上的两点,AE=CF,求证:BE=DF.【证明】∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS),
∴BE=DF.【想一想错在哪?】如图,线段AB,AD相交于点A,若过点B作BE∥AD,在BE上取一点C,使BC=AD,连接CD,则AC与BD的关系是
_________.提示:画图时考虑不周全而漏解,点C可能在点B的左侧,也可能在点B的右侧.
1.掌握平行四边形的对角线互相平分.(重点)
2.熟练应用平行四边形的性质进行计算或证明.(重点、难点)在?ABCD中,对角线AC,BD相交于点O.【思考】
1.平行四边形有哪些性质?
提示:平行四边形的对边相等,对角相等.
2.结合平行四边形的性质,你能判断△ABO与△CDO有怎样的关
系吗?
提示:全等.
3.由此可以得到哪些相等的线段?
提示:OA=OC,OB=OD.
【总结】平行四边形的性质:平行四边形的对角线_________.互相平分 (打“√”或“×”)
(1)平行四边形的对角线相等.( )
(2)平行四边形的对角线把平行四边形分成4个全等的三角
形.( )
(3)平行四边形的对角线平分一组对角.( )×××知识点 1 平行四边形的对角线互相平分
【例1】(2013·南充中考)如图,在?ABCD中,
对角线AC,BD交于点O,经过点O的直线交AB
于点E,交CD于点F.
求证:OE=OF.
【思路点拨】四边形ABCD是平行四边形→AO=CO,AB∥CD→△AOE≌△COF→OE=OF【自主解答】∵四边形ABCD是平行四边形,
∴AO=CO , AB∥CD,∴∠EAO=∠FCO,
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴OE=OF.
【总结提升】平行四边形性质的应用知识点 2 平行四边形性质的综合运用
【例2】(2013·海南中考)如图,在?ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )
A.BO=DO B.CD=AB
C.∠BAD=∠BCD D.AC=BD
【思路点拨】依据平行四边形的性质:对边平行且相等,对角相等,对角线互相平分,逐一判断即可.【自主解答】选D.根据平行四边形的对角线互相平分,可得BO=DO,选项A正确;根据平行四边形的对边相等,可得CD=AB,选项B正确;根据平行四边形的对角相等,可得∠BAD=∠BCD,选项C正确;而选项D中“AC=BD”说明对角线相等,平行四边形没有这一性质,因此选项D错误;故选D.【总结提升】平行四边形性质的综合运用
研究平行四边形的性质往往从边、角、对角线3个方面考虑:①边:平行四边形的对边平行且相等.②角:平行四边形的对角相等、邻角互补.③对角线:平行四边形的对角线互相平分.题组一:平行四边形的对角线互相平分
1.如图所示,在?ABCD中,对角线AC,BD交于点O,下列式子中一定成立的是( )
A.AO=OD B.OA=OC C.∠AOD=120° D.∠DOC=45°
【解析】选B.根据平行四边形的对角线互相平分可知一定成立的是选项B.2.如图所示,在平行四边形ABCD中,O为对角
线AC,BD的交点,与△AOD全等的是( )
A.△ABC B.△ADC
C.△BCD D.△COB
【解析】选D.∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,AD=BC,
∴△AOD≌△COB(ASA).3.如图,在平行四边形ABCD中,AC,BD为
对角线,BC=6,BC边上的高为4,则图中
阴影部分的面积为( )
A.3 B.6 C.12 D.24
【解析】选C.由于在平行四边形中,对边分别平行且相等,
对角线互相平分,图中的线段把平行四边形分成5组全等三角
形,通过仔细观察分析图中阴影部分,可得出每组全等三角形
中有一个带阴影,所以阴影部分的面积是平行四边形面积的一
半.所以S阴影= ×6×4=12.4.若点O为?ABCD的对角线AC与BD的交点,且AO+BO=11 cm,则AC+BD=_______cm.
【解析】∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴AC=2AO,BD=2BO,
∴AC+BD=2(AO+BO)=22 cm.
答案:225.如图,在四边形ABCD中,AB∥CD,
AD∥BC,AC,BD相交于点O.若AC=6,
则线段AO的长度等于_________.
【解析】∵在四边形ABCD中,AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵AC=6,
∴AO=
答案:36.如图所示,平行四边形ABCD的周长是18 cm,对角线AC,BD相交于点O,若△AOD与△AOB的周长差是5 cm,则边AB的长是_______cm.【解析】∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵△AOD的周长=OA+OD+AD,
△AOB的周长=OA+OB+AB,
又∵△AOD与△AOB的周长差是5 cm,
∴AD=AB+5,设AB=x,AD=5+x,
则2(x+5+x)=18,解得x=2,即AB=2 cm.
答案:27.如图,?ABCD和?EAFC的顶点D,B,E,F在同一条直线上.求证:DE=BF.
【证明】连接AC,交BD于O.
则OB=OD,OE=OF,
∴OD-OE=OB-OF,即DE=BF.题组二:平行四边形性质的综合运用
1.(2013·云南中考)如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论正确的是( )
A.S?ABCD=4S△AOB
B.AC=BD
C.AC⊥BD
D.平行四边形ABCD是轴对称图形【解析】选A.平行四边形两条对角线把它分成的四个三角形有两对全等三角形,但是这四个三角形的面积都是相等的,因为△AOD与△AOB是等底等高的,A正确;平行四边形的对角线互相平分,但不一定相等也不一定垂直,所以B,C错误;对于平行四边形不一定能找到一条直线,沿此直线折叠,使直线两旁的部分完全重合,所以它不一定是轴对称图形,D错误.故选A. 2.如图所示,?ABCD中,两条对角线AC,
BD相交于点O,AF⊥BD于F,CE⊥BD于E,
则图中全等三角形的对数共有( )
A.5对 B.6对 C.7对 D.8对
【解析】选C.∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OA=OC,OB=OD.
∴△ABD≌△CDB,△ACD≌△CAB,△AOB≌△COD,△AOD≌△COB.
∵AF⊥BD于F,CE⊥BD于E,
∴△ABF≌△CDE,△AFD≌△CEB,△AOF≌△COE.3.如图所示,在?ABCD中,E,F是对角线AC上的两点,AE=CF,求证:BE=DF.【证明】∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS),
∴BE=DF.【想一想错在哪?】如图,线段AB,AD相交于点A,若过点B作BE∥AD,在BE上取一点C,使BC=AD,连接CD,则AC与BD的关系是
_________.提示:画图时考虑不周全而漏解,点C可能在点B的左侧,也可能在点B的右侧.
