18.2.1 矩形(实例均为2013中考教师讲解典型题)课件
文档属性
| 名称 | 18.2.1 矩形(实例均为2013中考教师讲解典型题)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 666.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-16 23:45:01 | ||
图片预览






文档简介
课件28张PPT。矩形(第2课时) 1.能判断一个四边形为矩形.(重点)
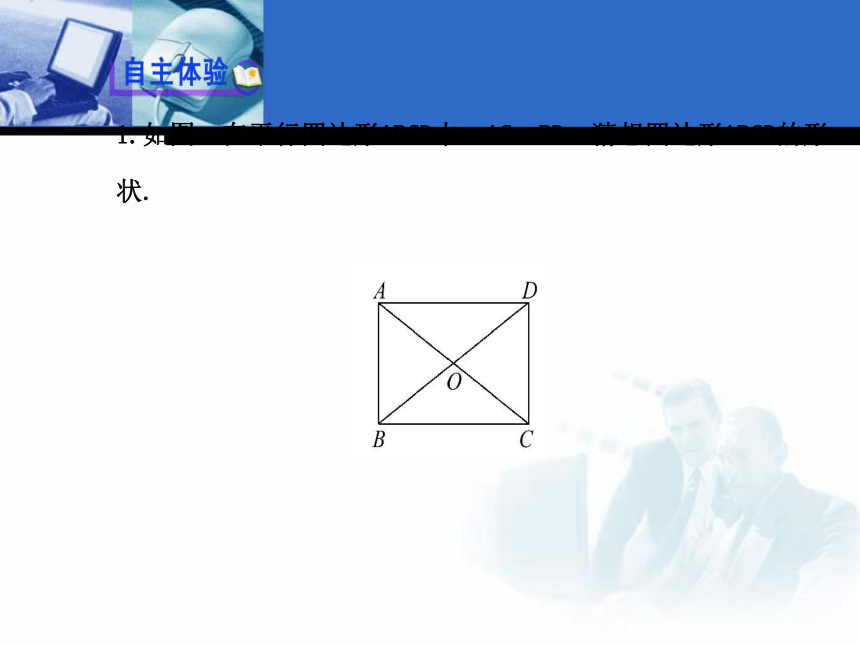
2.会用矩形的性质和判定定理进行计算或证明.(重点、难点)1.如图,在平行四边形ABCD中,AC=BD,猜想四边形ABCD的形状.【思考】(1)△ABC与△DCB有怎样的关系?
提示:全等
(2)∠ABC,∠DCB的度数是多少?
提示:∠ABC=∠DCB=90°.
(3)由此可判定四边形ABCD是哪种特殊平行四边形?
提示:矩形2.若一个四边形有三个内角是直角.
【思考】(1)这个四边形的第四个角是什么角?
提示:直角.
(2)这个四边形的两组对角相等,它是什么四边形?
提示:平行四边形.
(3)这个四边形是矩形吗?理由是什么?
提示:是.有一个角是直角的平行四边形是矩形.【总结】矩形的判定方法:
(1)有一个角是_____的平行四边形是矩形.
(2)对角线_____的平行四边形是矩形.
(3)有三个角是_____的四边形是矩形.直角相等直角 (打“√”或“×”)
(1)有一个角是直角的四边形是矩形.( )
(2)对角线相等的四边形是矩形.( )
(3)四个角都相等的四边形是矩形.( )
(4)对角线相等且互相平分的四边形是矩形.( )××√√知识点 矩形的判定
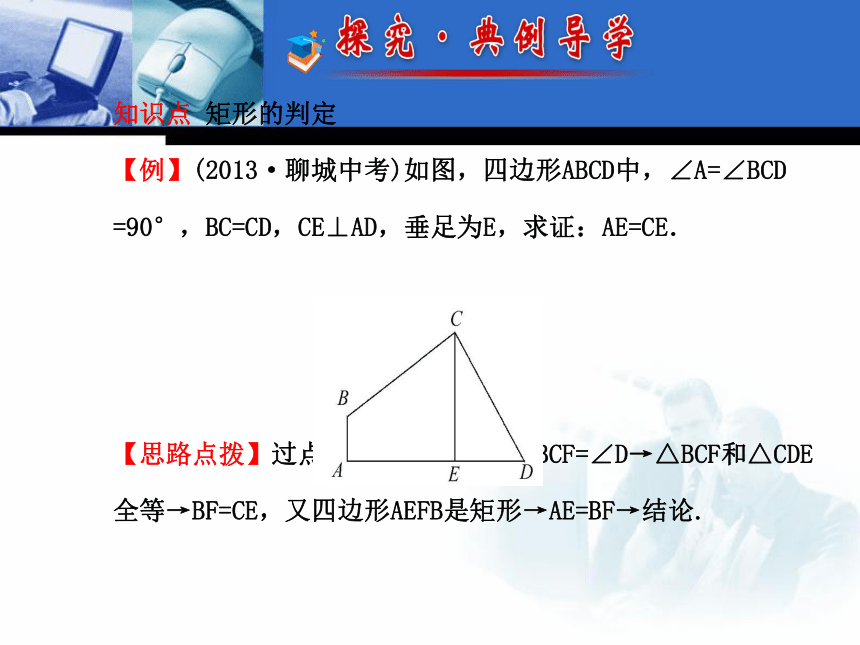
【例】(2013·聊城中考)如图,四边形ABCD中,∠A=∠BCD
=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.
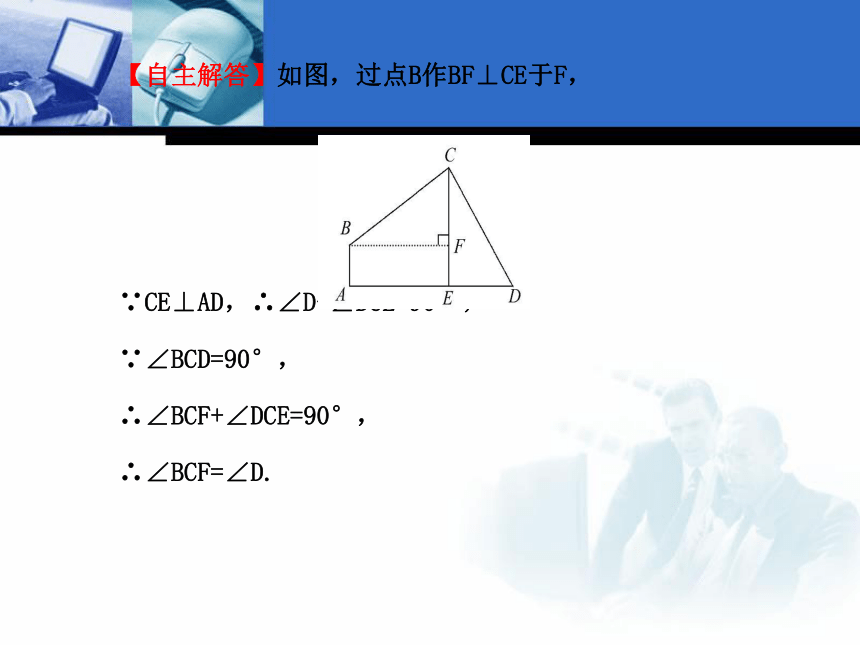
【思路点拨】过点B作BF⊥CE于F→∠BCF=∠D→△BCF和△CDE全等→BF=CE,又四边形AEFB是矩形→AE=BF→结论.【自主解答】如图,过点B作BF⊥CE于F,
∵CE⊥AD,∴∠D+∠DCE=90°,
∵∠BCD=90°,
∴∠BCF+∠DCE=90°,
∴∠BCF=∠D.在△BCF和△CDE中,
∴△BCF≌△CDE(AAS),
∴BF=CE.
又∵∠A=90°,CE⊥AD,BF⊥CE,
∴四边形AEFB是矩形,
∴AE=BF,∴AE=CE.【总结提升】矩形的判定方法题组:矩形的判定
1.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
【解析】选D.由条件知四边形ABCD是平行四边形,若AC=BD,即对角线相等,故是矩形.【变式备选】如图,四边形ABCD的对角线为AC,BD,且AC=BD,则下列条件能判定四边形ABCD是矩形的是( )
A.AB=BC
B.AC,BD互相平分
C.AC⊥BD
D.AB∥CD
【解析】选B.若AC,BD互相平分,则四边形ABCD是平行四边形,又AC=BD,故是矩形.2.如图,在四边形ABCD中,已知AB∥DC,AB=DC.在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是______________.(填上你认为正确的一个答案即可)【解析】答案不唯一,添加的条件可以是∠A=90°,
理由是:∵AB∥DC,AB=DC,
∴四边形ABCD是平行四边形,
∵∠A=90°,∴平行四边形ABCD是矩形.
答案:∠A=90°(答案不唯一)3.(2013·宿迁中考)如图,一个平行四边
形的活动框架,对角线是两根橡皮筋.若
改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为________度时,两条对角线长度相等.
【解析】根据对角线相等的平行四边形是矩形,可以得到∠α=90°.
答案:904.如图,已知E是?ABCD中BC边的中点,
连接AE并延长AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE.
(2)连接AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.【证明】(1)∵E是BC的中点,∴BE=CE.
∵四边形ABCD是平行四边形,∴AB∥DF,
∴∠BAE=∠CFE.
在△ABE与△FCE中
∴△ABE≌△FCE(AAS).(2)∵∠AEC=∠ABE+∠BAE,∠AEC=2∠ABC,
∴∠ABE=∠BAE,∴AE=BE.
∵△ABE≌△FCE,
∴AE=EF.∵BE=CE,
∴AE=EF=BE=CE,且AF=BC,
∴四边形ABFC为矩形.5.(2013·南通中考)如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:四边形BCDE是矩形.【证明】∵∠BAD=∠CAE,
∴∠BAD-∠BAC=∠CAE-∠BAC,
∴∠BAE=∠CAD.
∵在△BAE和△CAD中,
∴△BAE≌△CAD(SAS),
∴∠BEA=∠CDA,BE=CD,
∵DE=BC,∴四边形BCDE是平行四边形.∵AE=AD,∴∠AED=∠ADE,
∵∠BEA=∠CDA,∴∠BED=∠CDE,
∵四边形BCDE是平行四边形,
∴BE∥CD,
∴∠CDE+∠BED=180°,
∴∠BED=∠CDE=90°,
∴四边形BCDE是矩形.6.(2013·临沂中考)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC.
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.【解析】(1)∵E是AD的中点,∴AE=ED.
∵AF∥BC,∴∠AFE=∠DBE, ∠FAE=∠BDE,
∴△AFE≌△DBE,∴AF=DB.
∵AD是BC边上的中线,
∴DB=DC,∴AF=DC.(2)四边形ADCF是菱形.
证明:由(1)知,AF=DC,
∵AF∥CD,
∴四边形ADCF是平行四边形.
又∵AB⊥AC,
∴△ABC是直角三角形.
∵AD是BC边上的中线,
∴∴平行四边形ADCF是菱形.
即四边形ADCF是菱形.【想一想错在哪?】已知:如图,?ABCD各角的平分线分别相交于点E,F,G,H,求证:四边形EFGH是矩形.提示:一个角是90°的四边形不一定是矩形,还要说明它是平行四边形或还有另外两个角是直角.
2.会用矩形的性质和判定定理进行计算或证明.(重点、难点)1.如图,在平行四边形ABCD中,AC=BD,猜想四边形ABCD的形状.【思考】(1)△ABC与△DCB有怎样的关系?
提示:全等
(2)∠ABC,∠DCB的度数是多少?
提示:∠ABC=∠DCB=90°.
(3)由此可判定四边形ABCD是哪种特殊平行四边形?
提示:矩形2.若一个四边形有三个内角是直角.
【思考】(1)这个四边形的第四个角是什么角?
提示:直角.
(2)这个四边形的两组对角相等,它是什么四边形?
提示:平行四边形.
(3)这个四边形是矩形吗?理由是什么?
提示:是.有一个角是直角的平行四边形是矩形.【总结】矩形的判定方法:
(1)有一个角是_____的平行四边形是矩形.
(2)对角线_____的平行四边形是矩形.
(3)有三个角是_____的四边形是矩形.直角相等直角 (打“√”或“×”)
(1)有一个角是直角的四边形是矩形.( )
(2)对角线相等的四边形是矩形.( )
(3)四个角都相等的四边形是矩形.( )
(4)对角线相等且互相平分的四边形是矩形.( )××√√知识点 矩形的判定
【例】(2013·聊城中考)如图,四边形ABCD中,∠A=∠BCD
=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.
【思路点拨】过点B作BF⊥CE于F→∠BCF=∠D→△BCF和△CDE全等→BF=CE,又四边形AEFB是矩形→AE=BF→结论.【自主解答】如图,过点B作BF⊥CE于F,
∵CE⊥AD,∴∠D+∠DCE=90°,
∵∠BCD=90°,
∴∠BCF+∠DCE=90°,
∴∠BCF=∠D.在△BCF和△CDE中,
∴△BCF≌△CDE(AAS),
∴BF=CE.
又∵∠A=90°,CE⊥AD,BF⊥CE,
∴四边形AEFB是矩形,
∴AE=BF,∴AE=CE.【总结提升】矩形的判定方法题组:矩形的判定
1.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
【解析】选D.由条件知四边形ABCD是平行四边形,若AC=BD,即对角线相等,故是矩形.【变式备选】如图,四边形ABCD的对角线为AC,BD,且AC=BD,则下列条件能判定四边形ABCD是矩形的是( )
A.AB=BC
B.AC,BD互相平分
C.AC⊥BD
D.AB∥CD
【解析】选B.若AC,BD互相平分,则四边形ABCD是平行四边形,又AC=BD,故是矩形.2.如图,在四边形ABCD中,已知AB∥DC,AB=DC.在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是______________.(填上你认为正确的一个答案即可)【解析】答案不唯一,添加的条件可以是∠A=90°,
理由是:∵AB∥DC,AB=DC,
∴四边形ABCD是平行四边形,
∵∠A=90°,∴平行四边形ABCD是矩形.
答案:∠A=90°(答案不唯一)3.(2013·宿迁中考)如图,一个平行四边
形的活动框架,对角线是两根橡皮筋.若
改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为________度时,两条对角线长度相等.
【解析】根据对角线相等的平行四边形是矩形,可以得到∠α=90°.
答案:904.如图,已知E是?ABCD中BC边的中点,
连接AE并延长AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE.
(2)连接AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.【证明】(1)∵E是BC的中点,∴BE=CE.
∵四边形ABCD是平行四边形,∴AB∥DF,
∴∠BAE=∠CFE.
在△ABE与△FCE中
∴△ABE≌△FCE(AAS).(2)∵∠AEC=∠ABE+∠BAE,∠AEC=2∠ABC,
∴∠ABE=∠BAE,∴AE=BE.
∵△ABE≌△FCE,
∴AE=EF.∵BE=CE,
∴AE=EF=BE=CE,且AF=BC,
∴四边形ABFC为矩形.5.(2013·南通中考)如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:四边形BCDE是矩形.【证明】∵∠BAD=∠CAE,
∴∠BAD-∠BAC=∠CAE-∠BAC,
∴∠BAE=∠CAD.
∵在△BAE和△CAD中,
∴△BAE≌△CAD(SAS),
∴∠BEA=∠CDA,BE=CD,
∵DE=BC,∴四边形BCDE是平行四边形.∵AE=AD,∴∠AED=∠ADE,
∵∠BEA=∠CDA,∴∠BED=∠CDE,
∵四边形BCDE是平行四边形,
∴BE∥CD,
∴∠CDE+∠BED=180°,
∴∠BED=∠CDE=90°,
∴四边形BCDE是矩形.6.(2013·临沂中考)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC.
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.【解析】(1)∵E是AD的中点,∴AE=ED.
∵AF∥BC,∴∠AFE=∠DBE, ∠FAE=∠BDE,
∴△AFE≌△DBE,∴AF=DB.
∵AD是BC边上的中线,
∴DB=DC,∴AF=DC.(2)四边形ADCF是菱形.
证明:由(1)知,AF=DC,
∵AF∥CD,
∴四边形ADCF是平行四边形.
又∵AB⊥AC,
∴△ABC是直角三角形.
∵AD是BC边上的中线,
∴∴平行四边形ADCF是菱形.
即四边形ADCF是菱形.【想一想错在哪?】已知:如图,?ABCD各角的平分线分别相交于点E,F,G,H,求证:四边形EFGH是矩形.提示:一个角是90°的四边形不一定是矩形,还要说明它是平行四边形或还有另外两个角是直角.
