一次函数(第3课时)(实例均为2013中考教师讲解典型题)
文档属性
| 名称 | 一次函数(第3课时)(实例均为2013中考教师讲解典型题) |  | |
| 格式 | zip | ||
| 文件大小 | 671.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-12 08:21:09 | ||
图片预览











文档简介
课件30张PPT。一次函数(第3课时)1.会用待定系数法求一次函数的解析式.(重点)
2.灵活运用一次函数的有关知识解决相关实际问题.(重点、难点)已知一个一次函数当自变量x=3时,函数值y=5,当x=-4时,
y=-9.求这个一次函数的解析式.
设一次函数的解析式为_______,将题目中的两种关系代入
得:_____________
解得:_________
所以这个一次函数的解析式为_______.y=kx+by=2x-1【归纳】求一次函数解析式的步骤:
(1)先设出___________.
(2)再根据条件列出解析式中关于未知系数的方程.
(3)解方程,确定_________.
(4)根据求出的未知系数确定函数解析式.函数解析式未知系数 (打“√”或“×”)
(1)知道一点能确定一次函数y=kx-2的解析式.( )
(2)过点(-2,1)的一次函数有无数多个.( )
(3)过点(0,1)和点(1,0)的直线为y=x+1.( )
(4)经过原点的直线不是一次函数.( )√√××知识点 1 用待定系数法求一次函数解析式?
【例1】已知一次函数y=kx+b的图象经过点A(-1,3)和点
B(2,-3).求这个一次函数的解析式.
【思路点拨】把点A和点B的坐标代入y=kx+b得到关于k和b的二元一次方程组→解二元一次方程组→把k和b的值代入y=kx+b得一次函数解析式.【自主解答】依题意将A,B两点的坐标代入y=kx+b得
解得
∴所求一次函数的解析式是y=-2x+1.【总结提升】点的坐标在求函数解析式中的作用
(1)函数解析式与函数图象可以相互转化,实现这种转化的工具就是点的坐标.
(2)若已知图象上某点的坐标,就可以把该点的横、纵坐标作为解析式中的一对x,y的值,代入函数解析式,从而得到一个关于待定系数的方程.知识点 2 用一次函数解决实际问题?
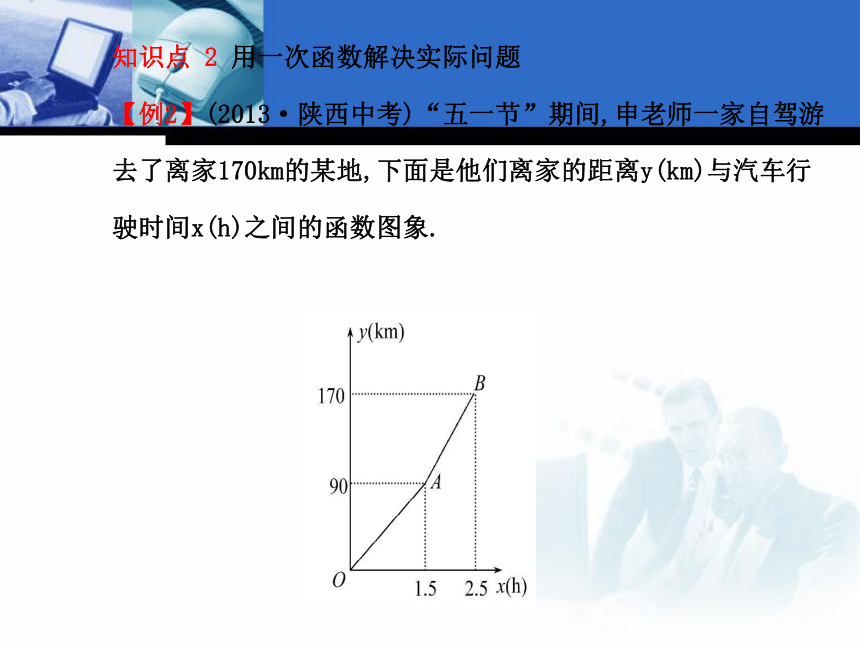
【例2】(2013·陕西中考)“五一节”期间,申老师一家自驾游去了离家170km的某地,下面是他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象.(1)求他们出发0.5h时,离家多少km.
(2)求出AB段图象的函数解析式.
(3)他们出发2h时,离目的地还有多少km.【解题探究】1.观察图象,若求OA的解析式,所给的条件有哪些?
提示:OA经过原点,是正比例函数,而OA经过点A(1.5,90),可求OA的解析式.
2.若求AB的解析式,所给的条件有哪些?
提示:由图象可得,AB经过点A(1.5,90)和点B(2.5,170).
3.出发2h,属于哪段函数问题?
提示:OA段的函数自变量取值范围为0≤x≤1.5,AB段的函数自变量取值范围为1.5≤x≤2.5,∴应将x=2代入AB段函数解析式求行驶的路程.4.请根据以上探究写出本题的解题过程:
提示:(1)设OA段图象的函数解析式为y=kx.
∵当x=1.5时,y=90,
∴1.5k=90,
∴k=60.
∴该段图象的函数解析式为y=60x,0≤x≤1.5,
∴当x=0.5时,y=60×0.5=30.
故他们出发0.5h时,离家30km.(2)设AB段图象的函数解析式为y=k′x+b.
∵A(1.5,90),B(2.5,170)在AB上,
∴
解得
∴AB段图象的函数解析式为
y=80x-30,1.5≤x≤2.5.(3)∵当x=2时,y=80×2-30=130,
∴170-130=40.
故他们出发2 h时,离目的地还有40 km.【总结提升】待定系数法在实际问题中应用的“两种情况”
(1)当问题已明确所求解的函数是一次函数时,便可用待定系数法.
(2)若函数的图象是线段(或直线),所求的函数就是一次函数,而且用待定系数法解答时,只需在线段(或直线)上找出两个已知点.题组一:用待定系数法求一次函数解析式
1.已知一次函数y=kx+b(k≠0)经过(2,-1),(-3,4)两点,则它的图象不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限【解析】选C.将(2,-1),(-3,4)代入一次函数y=kx+b中得:
解得
∴一次函数解析式为y=-x+1,其不经过第三象限.2.(2013·常州中考)已知一次函数y=kx+b(k,b为常数且k≠0)的图象经过点A(0,-2)和点B(1,0),则k= ,b= .
【解析】由题意得b=-2且k+b=0,所以k=2.
答案:2 -23.若一次函数y=(2-m)x+m的图象经过点(-1,0),则这个一次函数的解析式是 .
【解析】∵一次函数y=(2-m)x+m的图象经过点(-1,0),
∴0=(2-m)×(-1)+m,解得m=1,
∴这个一次函数的解析式是y=x+1.
答案:y=x+14.一次函数y=kx+b的图象与y轴交点的纵坐标为-3,且当x=1时,y=-1,则该一次函数的解析式是____________.
【解析】根据题意设y=kx-3,且当x=1时,y=-1,
∴-1=k-3,解得k=2.
∴该函数的解析式为y=2x-3.
答案:y=2x-35.求与直线y=x平行,并且经过点P(1,2)的一次函数的解析式.
【解析】根据题意,设一次函数解析式为y=kx+b,
∵该函数图象与直线y=x平行,∴k=1,
由经过点P(1,2)得:1+b=2,
解得:b=1,
∴该一次函数的解析式为y=x+1.题组二:用一次函数解决实际问题
1.弹簧的长度与所挂物体的质量关系为一次函数,由图可知,不挂物体时,弹簧的长度为( )
A.7cm B.8cm C.9cm D.10cm【解析】选D.设直线解析式为y=kx+b,由图象可知,直线过
(5,12.5),(20,20)两点,代入得
解得 即y=0.5x+10,当x=0时,y=10,
即不挂物体时,弹簧的长度为10 cm.2.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
A.20 kg B.25 kg
C.28 kg D.30 kg【解析】选A.设y与x的函数解析式为y=kx+b,
由题意可知
所以k=30,b=-600,
所以函数解析式为y=30x-600,
当y=0时,30x-600=0,所以x=20.3.如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(min)之间的函数关系,则通话8 min应付电话费__________元.【解析】由图象可得,点B(3,2.4),C(5,4.4),
设射线BC的解析式为y=kt+b(t≥3),
则 解得
所以,射线BC的解析式为y=t-0.6(t≥3),
当t=8时,y=8-0.6=7.4(元).
答案:7.44.(2013·湘潭中考)莲城超市以10元/件的价格调进一批商品,根据前期销售情况,每天销售量y(件)与该商品定价x(元)是一次函数关系,如图所示.
(1)求销售量y与定价x之间的函数解析式.
(2)如果超市将该商品的销售价定为13元/件,不考虑其他因素,求超市每天销售这种商品所获得的利润.【解析】(1)设y=kx+b(k≠0),
由图象可知,
解得
故销售量y与定价x之间的函数解析式是:
y=-2x+32.
(2)超市每天销售这种商品所获得的利润是:
W=(-2x+32)(13-10)=-6x+96.【想一想错在哪?】已知一次函数y=kx+4的图象与两坐标轴围成的三角形的面积为8,求一次函数的解析式.
提示:用点的坐标表示线段的长度时,要加上绝对值符号.
2.灵活运用一次函数的有关知识解决相关实际问题.(重点、难点)已知一个一次函数当自变量x=3时,函数值y=5,当x=-4时,
y=-9.求这个一次函数的解析式.
设一次函数的解析式为_______,将题目中的两种关系代入
得:_____________
解得:_________
所以这个一次函数的解析式为_______.y=kx+by=2x-1【归纳】求一次函数解析式的步骤:
(1)先设出___________.
(2)再根据条件列出解析式中关于未知系数的方程.
(3)解方程,确定_________.
(4)根据求出的未知系数确定函数解析式.函数解析式未知系数 (打“√”或“×”)
(1)知道一点能确定一次函数y=kx-2的解析式.( )
(2)过点(-2,1)的一次函数有无数多个.( )
(3)过点(0,1)和点(1,0)的直线为y=x+1.( )
(4)经过原点的直线不是一次函数.( )√√××知识点 1 用待定系数法求一次函数解析式?
【例1】已知一次函数y=kx+b的图象经过点A(-1,3)和点
B(2,-3).求这个一次函数的解析式.
【思路点拨】把点A和点B的坐标代入y=kx+b得到关于k和b的二元一次方程组→解二元一次方程组→把k和b的值代入y=kx+b得一次函数解析式.【自主解答】依题意将A,B两点的坐标代入y=kx+b得
解得
∴所求一次函数的解析式是y=-2x+1.【总结提升】点的坐标在求函数解析式中的作用
(1)函数解析式与函数图象可以相互转化,实现这种转化的工具就是点的坐标.
(2)若已知图象上某点的坐标,就可以把该点的横、纵坐标作为解析式中的一对x,y的值,代入函数解析式,从而得到一个关于待定系数的方程.知识点 2 用一次函数解决实际问题?
【例2】(2013·陕西中考)“五一节”期间,申老师一家自驾游去了离家170km的某地,下面是他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象.(1)求他们出发0.5h时,离家多少km.
(2)求出AB段图象的函数解析式.
(3)他们出发2h时,离目的地还有多少km.【解题探究】1.观察图象,若求OA的解析式,所给的条件有哪些?
提示:OA经过原点,是正比例函数,而OA经过点A(1.5,90),可求OA的解析式.
2.若求AB的解析式,所给的条件有哪些?
提示:由图象可得,AB经过点A(1.5,90)和点B(2.5,170).
3.出发2h,属于哪段函数问题?
提示:OA段的函数自变量取值范围为0≤x≤1.5,AB段的函数自变量取值范围为1.5≤x≤2.5,∴应将x=2代入AB段函数解析式求行驶的路程.4.请根据以上探究写出本题的解题过程:
提示:(1)设OA段图象的函数解析式为y=kx.
∵当x=1.5时,y=90,
∴1.5k=90,
∴k=60.
∴该段图象的函数解析式为y=60x,0≤x≤1.5,
∴当x=0.5时,y=60×0.5=30.
故他们出发0.5h时,离家30km.(2)设AB段图象的函数解析式为y=k′x+b.
∵A(1.5,90),B(2.5,170)在AB上,
∴
解得
∴AB段图象的函数解析式为
y=80x-30,1.5≤x≤2.5.(3)∵当x=2时,y=80×2-30=130,
∴170-130=40.
故他们出发2 h时,离目的地还有40 km.【总结提升】待定系数法在实际问题中应用的“两种情况”
(1)当问题已明确所求解的函数是一次函数时,便可用待定系数法.
(2)若函数的图象是线段(或直线),所求的函数就是一次函数,而且用待定系数法解答时,只需在线段(或直线)上找出两个已知点.题组一:用待定系数法求一次函数解析式
1.已知一次函数y=kx+b(k≠0)经过(2,-1),(-3,4)两点,则它的图象不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限【解析】选C.将(2,-1),(-3,4)代入一次函数y=kx+b中得:
解得
∴一次函数解析式为y=-x+1,其不经过第三象限.2.(2013·常州中考)已知一次函数y=kx+b(k,b为常数且k≠0)的图象经过点A(0,-2)和点B(1,0),则k= ,b= .
【解析】由题意得b=-2且k+b=0,所以k=2.
答案:2 -23.若一次函数y=(2-m)x+m的图象经过点(-1,0),则这个一次函数的解析式是 .
【解析】∵一次函数y=(2-m)x+m的图象经过点(-1,0),
∴0=(2-m)×(-1)+m,解得m=1,
∴这个一次函数的解析式是y=x+1.
答案:y=x+14.一次函数y=kx+b的图象与y轴交点的纵坐标为-3,且当x=1时,y=-1,则该一次函数的解析式是____________.
【解析】根据题意设y=kx-3,且当x=1时,y=-1,
∴-1=k-3,解得k=2.
∴该函数的解析式为y=2x-3.
答案:y=2x-35.求与直线y=x平行,并且经过点P(1,2)的一次函数的解析式.
【解析】根据题意,设一次函数解析式为y=kx+b,
∵该函数图象与直线y=x平行,∴k=1,
由经过点P(1,2)得:1+b=2,
解得:b=1,
∴该一次函数的解析式为y=x+1.题组二:用一次函数解决实际问题
1.弹簧的长度与所挂物体的质量关系为一次函数,由图可知,不挂物体时,弹簧的长度为( )
A.7cm B.8cm C.9cm D.10cm【解析】选D.设直线解析式为y=kx+b,由图象可知,直线过
(5,12.5),(20,20)两点,代入得
解得 即y=0.5x+10,当x=0时,y=10,
即不挂物体时,弹簧的长度为10 cm.2.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
A.20 kg B.25 kg
C.28 kg D.30 kg【解析】选A.设y与x的函数解析式为y=kx+b,
由题意可知
所以k=30,b=-600,
所以函数解析式为y=30x-600,
当y=0时,30x-600=0,所以x=20.3.如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(min)之间的函数关系,则通话8 min应付电话费__________元.【解析】由图象可得,点B(3,2.4),C(5,4.4),
设射线BC的解析式为y=kt+b(t≥3),
则 解得
所以,射线BC的解析式为y=t-0.6(t≥3),
当t=8时,y=8-0.6=7.4(元).
答案:7.44.(2013·湘潭中考)莲城超市以10元/件的价格调进一批商品,根据前期销售情况,每天销售量y(件)与该商品定价x(元)是一次函数关系,如图所示.
(1)求销售量y与定价x之间的函数解析式.
(2)如果超市将该商品的销售价定为13元/件,不考虑其他因素,求超市每天销售这种商品所获得的利润.【解析】(1)设y=kx+b(k≠0),
由图象可知,
解得
故销售量y与定价x之间的函数解析式是:
y=-2x+32.
(2)超市每天销售这种商品所获得的利润是:
W=(-2x+32)(13-10)=-6x+96.【想一想错在哪?】已知一次函数y=kx+4的图象与两坐标轴围成的三角形的面积为8,求一次函数的解析式.
提示:用点的坐标表示线段的长度时,要加上绝对值符号.
