19.1.1 函数(实例均为2013中考教师讲解典型题)课件
文档属性
| 名称 | 19.1.1 函数(实例均为2013中考教师讲解典型题)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 677.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-16 00:00:00 | ||
图片预览









文档简介
课件36张PPT。 函数的图象(第2课时)1.了解表示函数的三种方法.(重点)
2.能根据具体情况选用适当的方法表示函数.会用函数相关知识解决实际问题.(重点、难点)根据下列问题填空:
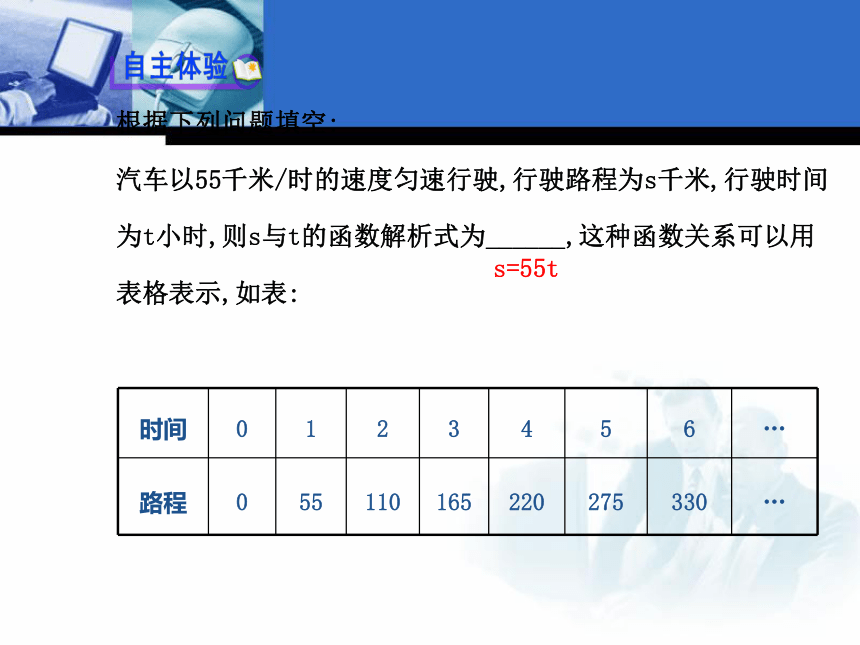
汽车以55千米/时的速度匀速行驶,行驶路程为s千米,行驶时间
为t小时,则s与t的函数解析式为______,这种函数关系可以用
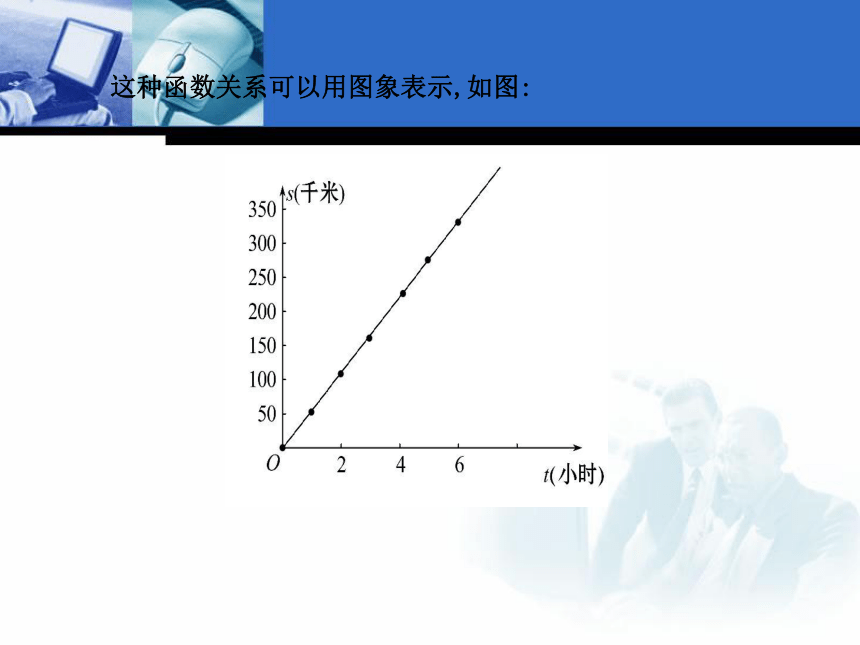
表格表示,如表:s=55t这种函数关系可以用图象表示,如图:【思考】以上问题分别用了哪几种方法表示函数关系?
提示:一是用含自变量t的代数式表示s的方法;二是把一些自变
量t和其对应的函数值s列成一个表格来表示的;三是用图象来
表示函数关系.
【总结】表示函数的方法有三种,分别是_________、_______、
_______.解析式法列表法图象法 (打“√”或“×”)
(1)每种函数关系都可以用解析式法来表示.( )
(2)两个变量间的关系只能用解析式表示.( )
(3)借助表格可以表示出函数值随自变量的变化情况.( )
(4)图象能直观地表示两个变量间的数量关系.( )××√×知识点 1 函数的三种表示方法?
【例1】1~6个月的婴儿生长发育得非常快,他们的体重y(克)和月龄x(月)间的关系可以用y=a+700x表示,其中a是婴儿出生时的体重.假设一个婴儿出生时的体重为4000克.
(1)请用表格表示,在1~6个月内,这个婴儿的体重y与月龄x之间的关系.
(2)请指出这个关系式中的常量和变量,并指出变量之间存在什么关系.【思路点拨】(1)把x的值分别代入y=4000+700x求值即可.
(2)由关系式及表格确定常量、变量以及变量之间的关系.【自主解答】(1)这个婴儿的体重y与月龄x之间的关系如表所示:
(2)因为y与x之间的关系式是y=4000+700x,所以常量是4000和700,变量是y与x,由表格可以看出对于变量x的每一个值,变量y都有唯一的值与它对应,因此y是x的函数.【总结提升】函数三种表示方法的选用技巧
(1)列表法:需要直接用部分函数值表达函数关系时选用列表法.
(2)图象法:需要明显表现函数变化趋势时选用图象法.
(3)解析式法:需要明显表现自变量与函数的对应规律时选用解析式法.知识点 2 用函数知识解决问题?
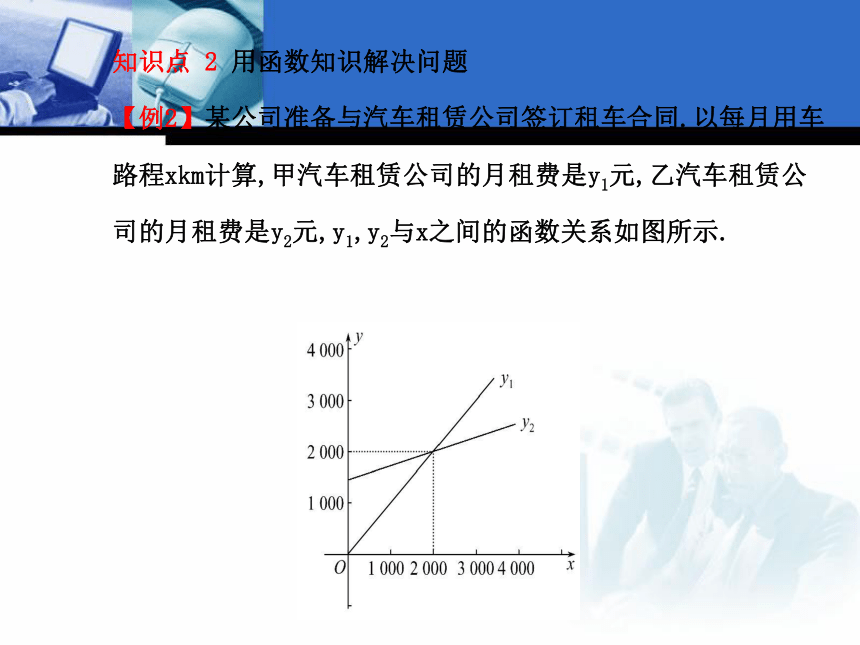
【例2】某公司准备与汽车租赁公司签订租车合同.以每月用车路程xkm计算,甲汽车租赁公司的月租费是y1元,乙汽车租赁公司的月租费是y2元,y1,y2与x之间的函数关系如图所示.(1)每月用车路程为 km时,租用两家汽车租赁公司的车所需的费用相同.
(2)若每月用车的路程约为2300km,那么租用哪家的车所需的费用较少?为什么?【解题探究】
(1)①从图象中可否看出,表示两家汽车租赁公司的车所需费用相同的点?
提示:当直线y1,y2相交时,两家汽车租赁公司的车所需的费用相同,交点的横坐标为每月用车路程.
②当x取何值时,租用两家汽车租赁公司的车所需费用相同?
提示:由图象可得,交点的坐标为(2000,2000),即每月用车路程为2000km时,租用两家汽车租赁公司的车所需的费用相同.(2)①要比较两家汽车租赁公司的车所需费用的多少,是否需要求出具体的费用?
提示:不用求,根据图象找到当x=2300时,两个函数图象所对应的点,比较两个点的纵坐标即可.
②若每月用车的路程约为2300km,那么租用哪家的车所需的费用较少?
提示:当x=2300时,y1>y2,∴y2较小.即每月用车的路程约为2300km时,租用乙汽车租赁公司的车所需的费用较少.【总结提升】利用函数知识解决实际问题的步骤
(1)理解题意,注意问题中变量之间的数量关系.
(2)观察图象,特别是图象中的常量、变量以及两坐标轴表示的意义等.
(3)对这些信息进行处理,解决问题.题组一:函数的三种表示方法
1.在某次实验中,测得两个变量m和v之间的4组对应数据如表.则m与v之间的关系最接近于下列各关系式中的( )
A.v=2m-2 B.v=m2-1
C.v=3m-3 D.v=m+1【解析】选B.当m=4时,A.v=2m-2=6;B.v=m2-1=15;C.v=3m-3=9;D.v=m+1=5.故选B.2.下列表格列出了一项实验的统计数据,它表示皮球从一定高度落下时,下落高度y与弹跳高度x的关系,能表示这种关系的函数解析式为( )
A.y=x2 B.y=2x-10
C.y=x+25 D.y= x+5【解析】选B.当x=30时,y=2×30-10=50;当x=45时,y=2×45-10=80;当x=55时,y=2×55-10=100;当x=80时,y=2×80-10=150;都能成立.3.(2013·佛山中考)某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )【解析】选B.图象应分三个阶段,第一阶段:匀速跑步到公园,在这个阶段,离家的距离随时间的增加而增大;
第二阶段:在公园停留了一段时间,这一阶段离家的距离不随时间的变化而改变.故D错误;
第三阶段:沿原路匀速步行回家,这一阶段,离家的距离随时间的增加而减小,故A错误,并且这个阶段的速度小于第一阶段的速度,则C错误.4.图中的圆点是有规律地从里到外逐层排列的.设y为第n层(n为正整数)圆点的个数,则y与n之间的函数解析式为y=______.【解析】因为对于每一个x的值,y都有唯一的值和它相对应,可以发现:圆点个数是所在层数的4倍.
所以y与n之间的函数解析式是y=4n.
答案:4n题组二:用函数知识解决问题
1.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数
据:
设鸭的质量为xkg,烤制时间为tmin,估计当x=3.2时,t的值为
( )
A.144 B.146 C.148 D.149【解析】选C.从表中可以看出,烤鸭的质量每增加0.5kg,烤制的时间增加20min,则t与x的函数解析式为t=40x+20.
当x=3.2时,t=40×3.2+20=148.2.(2013·哈尔滨中考)梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10kg以上(不含10kg)的种子,超过10kg的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:kg)之间的函数关系如图所示.下列四种说法:①一次购买种子数量不超过10kg时,销售价格为5元/kg;
②一次购买30kg种子时,付款金额为100元;
③一次购买10kg以上种子时,超过10kg的那部分种子的价格打五折;
④一次购买40kg种子比分两次购买且每次购买20kg种子少花25元钱.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个【解析】选D.一次购买种子数量不超过10kg时,销售价格为50÷10=5(元/kg),①正确;一次购买10kg以上种子时,超过10kg的那部分种子的销售价格为(150-50)÷(50-10)=2.5(元/kg),所以购买30kg种子的金额为5×10+2.5×20=100(元),②正确;超过10kg的那部分种子的销售价格为2.5元/kg,所以超过10kg的那部分种子的价格打五折,③正确;一次购买40kg种子的金额为5×10+2.5×30=125(元),分两次购买且每次购买20kg种子的金额为2×(5×10+2.5×10)=150(元),150-125=25(元),④正确.故选D.3.甲、乙两个工程队完成某项工程,首先是甲队单独做了10天,然后乙队加入共同完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系,那么实际完成这项工程所用的时间比由甲队单独完成这项工程所需时间少 天.【解析】由图象知甲队10天完成工程的 ,所以甲队单独完成
这项工程需40天;甲乙两队合做4天完成工程的 ,所以甲乙两
队完成14天后的工程还需8天,这样实际完成这项工程用22天.
因此实际完成这项工程所用的时间比由甲队单独完成这项工程
所需时间少18天.
答案:184.如图,OA,BA分别表示甲、乙两名学生匀速跑步运动的函数图象,图中s和t分别表示运动路程和时间,根据图象判断跑步快者比慢者每秒快 m.【解析】根据图象跑步快者经过8s追上慢者,并且快的比慢的多跑12m,12÷8=1.5(m).
答案:1.55.某市区内乘出租车的价格y(元)与路程x(km)的函数关系如图所示.
(1)根据图象写出两条信息.
(2)小明从学校出发乘出租车回家用了13元,求学校离小明家的路程.【解析】(1)不超过2km的路程付费5元;多于2km的路程,每千米1÷0.625=1.6(元).
(2)由图象知多于2km的路程为(13-5)÷1.6=5km.故学校离小明家的路程为7km.【想一想错在哪?】如图所示是自行车行驶路程与时间的关系 图,则整个过程的平均速度是多少?提示:只算了自行车行驶的时间,把中间一个小时的休息时间没算在整个过程中出错.
2.能根据具体情况选用适当的方法表示函数.会用函数相关知识解决实际问题.(重点、难点)根据下列问题填空:
汽车以55千米/时的速度匀速行驶,行驶路程为s千米,行驶时间
为t小时,则s与t的函数解析式为______,这种函数关系可以用
表格表示,如表:s=55t这种函数关系可以用图象表示,如图:【思考】以上问题分别用了哪几种方法表示函数关系?
提示:一是用含自变量t的代数式表示s的方法;二是把一些自变
量t和其对应的函数值s列成一个表格来表示的;三是用图象来
表示函数关系.
【总结】表示函数的方法有三种,分别是_________、_______、
_______.解析式法列表法图象法 (打“√”或“×”)
(1)每种函数关系都可以用解析式法来表示.( )
(2)两个变量间的关系只能用解析式表示.( )
(3)借助表格可以表示出函数值随自变量的变化情况.( )
(4)图象能直观地表示两个变量间的数量关系.( )××√×知识点 1 函数的三种表示方法?
【例1】1~6个月的婴儿生长发育得非常快,他们的体重y(克)和月龄x(月)间的关系可以用y=a+700x表示,其中a是婴儿出生时的体重.假设一个婴儿出生时的体重为4000克.
(1)请用表格表示,在1~6个月内,这个婴儿的体重y与月龄x之间的关系.
(2)请指出这个关系式中的常量和变量,并指出变量之间存在什么关系.【思路点拨】(1)把x的值分别代入y=4000+700x求值即可.
(2)由关系式及表格确定常量、变量以及变量之间的关系.【自主解答】(1)这个婴儿的体重y与月龄x之间的关系如表所示:
(2)因为y与x之间的关系式是y=4000+700x,所以常量是4000和700,变量是y与x,由表格可以看出对于变量x的每一个值,变量y都有唯一的值与它对应,因此y是x的函数.【总结提升】函数三种表示方法的选用技巧
(1)列表法:需要直接用部分函数值表达函数关系时选用列表法.
(2)图象法:需要明显表现函数变化趋势时选用图象法.
(3)解析式法:需要明显表现自变量与函数的对应规律时选用解析式法.知识点 2 用函数知识解决问题?
【例2】某公司准备与汽车租赁公司签订租车合同.以每月用车路程xkm计算,甲汽车租赁公司的月租费是y1元,乙汽车租赁公司的月租费是y2元,y1,y2与x之间的函数关系如图所示.(1)每月用车路程为 km时,租用两家汽车租赁公司的车所需的费用相同.
(2)若每月用车的路程约为2300km,那么租用哪家的车所需的费用较少?为什么?【解题探究】
(1)①从图象中可否看出,表示两家汽车租赁公司的车所需费用相同的点?
提示:当直线y1,y2相交时,两家汽车租赁公司的车所需的费用相同,交点的横坐标为每月用车路程.
②当x取何值时,租用两家汽车租赁公司的车所需费用相同?
提示:由图象可得,交点的坐标为(2000,2000),即每月用车路程为2000km时,租用两家汽车租赁公司的车所需的费用相同.(2)①要比较两家汽车租赁公司的车所需费用的多少,是否需要求出具体的费用?
提示:不用求,根据图象找到当x=2300时,两个函数图象所对应的点,比较两个点的纵坐标即可.
②若每月用车的路程约为2300km,那么租用哪家的车所需的费用较少?
提示:当x=2300时,y1>y2,∴y2较小.即每月用车的路程约为2300km时,租用乙汽车租赁公司的车所需的费用较少.【总结提升】利用函数知识解决实际问题的步骤
(1)理解题意,注意问题中变量之间的数量关系.
(2)观察图象,特别是图象中的常量、变量以及两坐标轴表示的意义等.
(3)对这些信息进行处理,解决问题.题组一:函数的三种表示方法
1.在某次实验中,测得两个变量m和v之间的4组对应数据如表.则m与v之间的关系最接近于下列各关系式中的( )
A.v=2m-2 B.v=m2-1
C.v=3m-3 D.v=m+1【解析】选B.当m=4时,A.v=2m-2=6;B.v=m2-1=15;C.v=3m-3=9;D.v=m+1=5.故选B.2.下列表格列出了一项实验的统计数据,它表示皮球从一定高度落下时,下落高度y与弹跳高度x的关系,能表示这种关系的函数解析式为( )
A.y=x2 B.y=2x-10
C.y=x+25 D.y= x+5【解析】选B.当x=30时,y=2×30-10=50;当x=45时,y=2×45-10=80;当x=55时,y=2×55-10=100;当x=80时,y=2×80-10=150;都能成立.3.(2013·佛山中考)某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )【解析】选B.图象应分三个阶段,第一阶段:匀速跑步到公园,在这个阶段,离家的距离随时间的增加而增大;
第二阶段:在公园停留了一段时间,这一阶段离家的距离不随时间的变化而改变.故D错误;
第三阶段:沿原路匀速步行回家,这一阶段,离家的距离随时间的增加而减小,故A错误,并且这个阶段的速度小于第一阶段的速度,则C错误.4.图中的圆点是有规律地从里到外逐层排列的.设y为第n层(n为正整数)圆点的个数,则y与n之间的函数解析式为y=______.【解析】因为对于每一个x的值,y都有唯一的值和它相对应,可以发现:圆点个数是所在层数的4倍.
所以y与n之间的函数解析式是y=4n.
答案:4n题组二:用函数知识解决问题
1.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数
据:
设鸭的质量为xkg,烤制时间为tmin,估计当x=3.2时,t的值为
( )
A.144 B.146 C.148 D.149【解析】选C.从表中可以看出,烤鸭的质量每增加0.5kg,烤制的时间增加20min,则t与x的函数解析式为t=40x+20.
当x=3.2时,t=40×3.2+20=148.2.(2013·哈尔滨中考)梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10kg以上(不含10kg)的种子,超过10kg的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:kg)之间的函数关系如图所示.下列四种说法:①一次购买种子数量不超过10kg时,销售价格为5元/kg;
②一次购买30kg种子时,付款金额为100元;
③一次购买10kg以上种子时,超过10kg的那部分种子的价格打五折;
④一次购买40kg种子比分两次购买且每次购买20kg种子少花25元钱.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个【解析】选D.一次购买种子数量不超过10kg时,销售价格为50÷10=5(元/kg),①正确;一次购买10kg以上种子时,超过10kg的那部分种子的销售价格为(150-50)÷(50-10)=2.5(元/kg),所以购买30kg种子的金额为5×10+2.5×20=100(元),②正确;超过10kg的那部分种子的销售价格为2.5元/kg,所以超过10kg的那部分种子的价格打五折,③正确;一次购买40kg种子的金额为5×10+2.5×30=125(元),分两次购买且每次购买20kg种子的金额为2×(5×10+2.5×10)=150(元),150-125=25(元),④正确.故选D.3.甲、乙两个工程队完成某项工程,首先是甲队单独做了10天,然后乙队加入共同完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系,那么实际完成这项工程所用的时间比由甲队单独完成这项工程所需时间少 天.【解析】由图象知甲队10天完成工程的 ,所以甲队单独完成
这项工程需40天;甲乙两队合做4天完成工程的 ,所以甲乙两
队完成14天后的工程还需8天,这样实际完成这项工程用22天.
因此实际完成这项工程所用的时间比由甲队单独完成这项工程
所需时间少18天.
答案:184.如图,OA,BA分别表示甲、乙两名学生匀速跑步运动的函数图象,图中s和t分别表示运动路程和时间,根据图象判断跑步快者比慢者每秒快 m.【解析】根据图象跑步快者经过8s追上慢者,并且快的比慢的多跑12m,12÷8=1.5(m).
答案:1.55.某市区内乘出租车的价格y(元)与路程x(km)的函数关系如图所示.
(1)根据图象写出两条信息.
(2)小明从学校出发乘出租车回家用了13元,求学校离小明家的路程.【解析】(1)不超过2km的路程付费5元;多于2km的路程,每千米1÷0.625=1.6(元).
(2)由图象知多于2km的路程为(13-5)÷1.6=5km.故学校离小明家的路程为7km.【想一想错在哪?】如图所示是自行车行驶路程与时间的关系 图,则整个过程的平均速度是多少?提示:只算了自行车行驶的时间,把中间一个小时的休息时间没算在整个过程中出错.
