19.2.3一次函数与方程、不等式(实例均为2013中考教师讲解典型题)课件 新人教版
文档属性
| 名称 | 19.2.3一次函数与方程、不等式(实例均为2013中考教师讲解典型题)课件 新人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 772.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-17 12:05:13 | ||
图片预览










文档简介
课件33张PPT。 一次函数与方程、不等式
(第2课时)1.会根据一次函数图象求一元一次不等式的解集,会求二元一次方程的解.(重点)
2.理解一次函数与一元一次不等式、二元一次方程的关系.(重点、难点)一、一次函数与一元一次不等式的关系
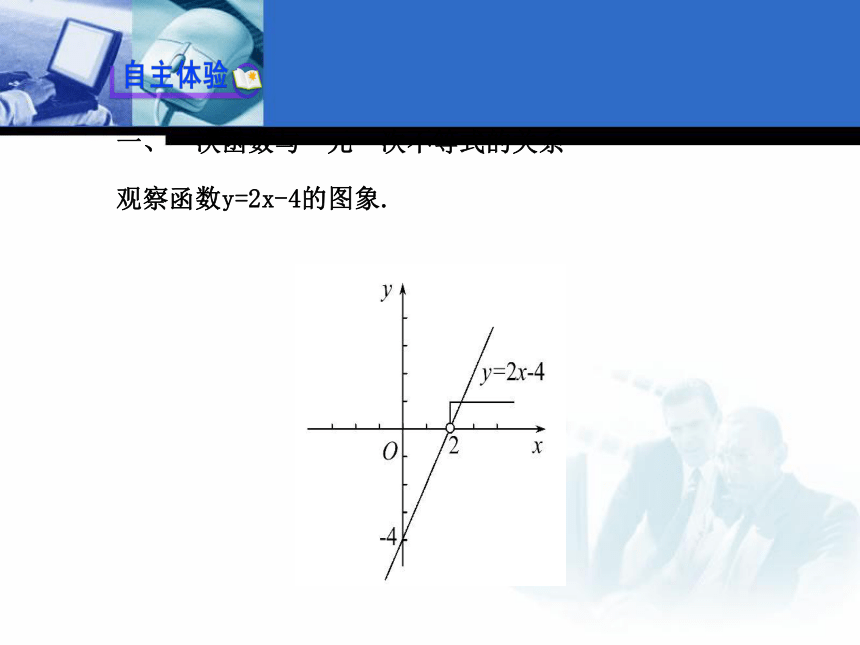
观察函数y=2x-4的图象.【思考】1.当自变量x取何值时,函数值大于0?
提示:当x>2时,直线y=2x-4上的点全在x轴上方,即这时y=2x-4>0.
2.当自变量x取何值时,函数值小于0?
提示:当x<2时,直线y=2x-4上的点全在x轴下方,即这时y=2x-4<0.【总结】任何一个以x为未知数的一元一次不等式都可以变形
为_______________(a≠0)的形式,所以解一元一次不等式相当
于在某个一次函数_______的值大于0或小于0时,求自变量x的
取值范围.ax+b>0或ax+b<0y=ax+b二、一次函数与二元一次方程组
1.每一个含有未知数x和y的二元一次方程,都可以改写为
_______________________的形式,所以每个这样的方程都对应
一个一次函数,于是也对应一条_____,这条直线上每个点的坐
标(x,y)都是这个二元一次方程的解.
2.含有未知数x和y的两个二元一次方程组成的方程组的解,是
对应的两个一次函数图象交点的坐标.y=kx+b(k,b是常数,k≠0)直线 (打“√”或“×”)
(1)函数值大于0的点都在x轴的上方.( )
(2)由直线y=x-b与x轴交于点(3,0),知x-b>0的解集为x>
3.( )
(3)以x+y=2的解组成坐标的点都在直线y=x-2上.( )
(4)方程组 没有解,则一次函数y=2-x与
的图象必定平行.( )√√×√知识点 1 用函数图象的方法解不等式?
【例1】用画一次函数图象的方法解不等式2x+1>3x+4.
【思路点拨】将不等式转化为kx+b>0的形式→画相应函数y=kx+b的图象→得到相应自变量的取值范围.【自主解答】原不等式可化为:-x-3>0,
画出函数y=-x-3的图象
从图象可以看出,当x<-3时这条直线上的点在x轴的上方,即此时-x-3>0,因此不等式2x+1>3x+4的解集是x<-3.【总结提升】用图象法解不等式的“三字诀”知识点 2 用函数图象的方法解二元一次方程组
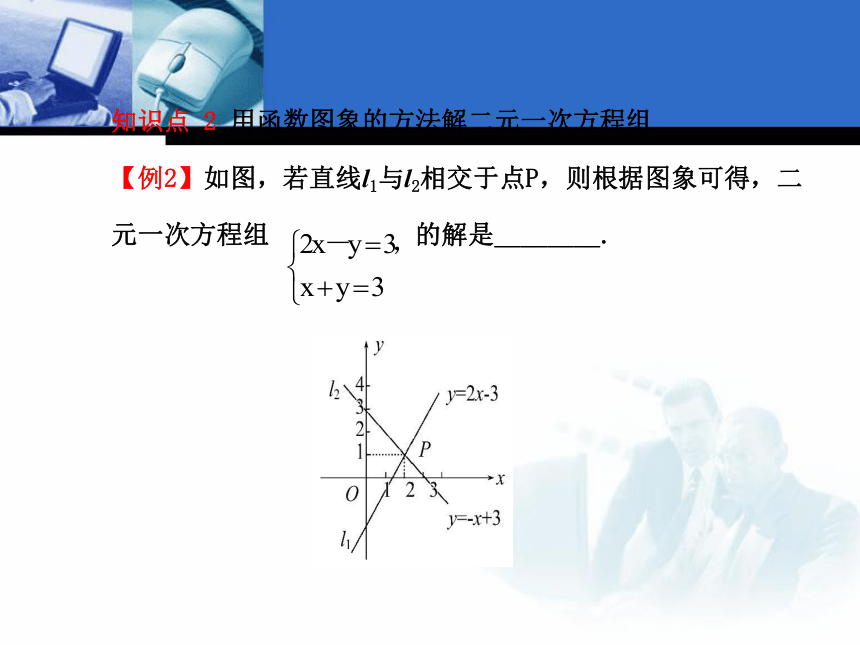
【例2】如图,若直线l1与l2相交于点P,则根据图象可得,二
元一次方程组 的解是________.【解题探究】1.二元一次方程2x-y=3与一次函数y=2x-3有什么关系?
提示:这条直线y=2x-3上每个点的坐标(x,y)都是这个二元一次方程2x-y=3的解.
2.二元一次方程 x+y=3与一次函数y=-x+3有什么关系?
提示:这条直线y=-x+3上每个点的坐标(x,y)都是这个二元一次方程x+y=3的解.3.方程组 与一次函数y=2x-3和一次函数y=-x+3有
什么关系?
提示:这两条直线的交点的坐标(x,y)就是方程组
的解.
4.直线y=2x-3和直线y=-x+3的交点为_______,所以方程组
的解为________(2,1)【总结提升】用图象法确定二元一次方程组的解
(1)将两个方程都化为y=kx+b(k,b是常数,k≠0)的形式.
(2)画出两个函数的图象,确定交点坐标.
(3)两个一次函数图象交点的坐标是这个二元一次方程组的解.题组一:用函数图象的方法解不等式
1.(2013·娄底中考)一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( )
A.x<0 B.x>0 C.x<2 D.x>2【解析】选C.y>0对应一次函数图象在x轴上方,自变量的范围是x<2.2.(2013·铜仁中考)如图,直线y=kx+b交坐标
轴于A(-2,0),B(0,3)两点,则不等式kx+b>0的
解集是( )
A.x>3 B.-2C.x<-2 D.x>-2
【解析】选D.由函数图象可知,y=kx+b交x轴于(-2,0),
所以当x>-2时,y>0,即kx+b>0.3.如图,函数y=ax-1的图象过点(1,2),则
不等式ax-1>2的解集是 .
【解析】根据图象可知:y=ax-1>2的x的
取值范围是x>1,
即不等式ax-1>2的解集是x>1.
答案:x>14.如图,直线l1:y=x+1与直线l2:y=mx+n相
交于点P(a,2),则关于x的不等式x+1≥mx
+n的解集为 .
【解析】把y=2代入y=x+1,得x=1,
∴点P的坐标为(1,2),
根据图象可知当x≥1时,y=x+1的函数值大于y=mx+n相应的函数值.
因而不等式x+1≥mx+n的解集是:x≥1.
答案:x≥15.兄弟俩赛跑,开始前,弟弟在哥哥前方9m,已知弟弟每秒跑3m,哥哥每秒跑4m,列出函数关系式,画出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过100m?【解析】设兄弟俩赛跑的时间为x秒.哥哥跑过的路程为y1,弟弟跑过的路程为y2,根据题意,得y1=4x,y2=3x+9.函数图象如图:
从图象上来看:(1)当09时,哥哥跑在弟弟前面.
(3)弟弟先跑过20m,哥哥先跑过100m.题组二:用函数图象的方法解二元一次方程组
1.两条直线y=k1x+b1和y=k2x+b2相交于点A(-2,3),则方程组
的解是( )【解析】选B.∵两条直线y=k1x+b1和y=k2x+b2相交于点A(-2,
3),
∴x=-2,y=3就是方程组 的解.
∴方程组 的解为2.如图,以两条直线l1,l2的交点坐标为解的方程组是( )【解析】选C.直线l1经过(2,3),(0,-1),易知其函数解析式
为y=2x-1;直线l2经过(2,3),(0,1),易知其函数解析式为
y=x+1;因此以两条直线l1,l2的交点坐标为解的方程组可以
是:3.函数y=2x-3的图象上任意一点的坐标都一定满足二元一次方程:_________.
【解析】y=2x-3移项得2x-y-3=0.
答案:2x-y-3=04.如图,已知一次函数y=ax+b和正比例函数y=kx的图象交于点
P,则根据图象可得二元一次方程组 的解是_____.【解析】根据题意可知,二元一次方程组 的解就
是一次函数y=ax+b和正比例函数y=kx图象的交点P的坐标,由
一次函数y=ax+b和正比例函数y=kx的图象的交点为(-4,-2),
可得二元一次方程组 的解是
答案:5.已知两直线y1=2x-3,y2=6-x,
(1)在同一坐标系中作出它们的图象.
(2)求它们的交点A的坐标.
(3)根据图象指出x为何值时,y1>y2;x为何值时,y1(4)求这两条直线与x轴所围成的三角形的面积.【解析】(1)如图:(2)解方程组 得
∴A(3,3).
(3)当x>3时,y1>y2;当x<3时,y1(4)可求得 C(6,0),
则【想一想错在哪?】当自变量x满足什么条件时,一次函数
y=-2x+4的值满足y>-2?
提示:读图不认真,x>2时,对应的函数值在x轴下方,即y<0.
(第2课时)1.会根据一次函数图象求一元一次不等式的解集,会求二元一次方程的解.(重点)
2.理解一次函数与一元一次不等式、二元一次方程的关系.(重点、难点)一、一次函数与一元一次不等式的关系
观察函数y=2x-4的图象.【思考】1.当自变量x取何值时,函数值大于0?
提示:当x>2时,直线y=2x-4上的点全在x轴上方,即这时y=2x-4>0.
2.当自变量x取何值时,函数值小于0?
提示:当x<2时,直线y=2x-4上的点全在x轴下方,即这时y=2x-4<0.【总结】任何一个以x为未知数的一元一次不等式都可以变形
为_______________(a≠0)的形式,所以解一元一次不等式相当
于在某个一次函数_______的值大于0或小于0时,求自变量x的
取值范围.ax+b>0或ax+b<0y=ax+b二、一次函数与二元一次方程组
1.每一个含有未知数x和y的二元一次方程,都可以改写为
_______________________的形式,所以每个这样的方程都对应
一个一次函数,于是也对应一条_____,这条直线上每个点的坐
标(x,y)都是这个二元一次方程的解.
2.含有未知数x和y的两个二元一次方程组成的方程组的解,是
对应的两个一次函数图象交点的坐标.y=kx+b(k,b是常数,k≠0)直线 (打“√”或“×”)
(1)函数值大于0的点都在x轴的上方.( )
(2)由直线y=x-b与x轴交于点(3,0),知x-b>0的解集为x>
3.( )
(3)以x+y=2的解组成坐标的点都在直线y=x-2上.( )
(4)方程组 没有解,则一次函数y=2-x与
的图象必定平行.( )√√×√知识点 1 用函数图象的方法解不等式?
【例1】用画一次函数图象的方法解不等式2x+1>3x+4.
【思路点拨】将不等式转化为kx+b>0的形式→画相应函数y=kx+b的图象→得到相应自变量的取值范围.【自主解答】原不等式可化为:-x-3>0,
画出函数y=-x-3的图象
从图象可以看出,当x<-3时这条直线上的点在x轴的上方,即此时-x-3>0,因此不等式2x+1>3x+4的解集是x<-3.【总结提升】用图象法解不等式的“三字诀”知识点 2 用函数图象的方法解二元一次方程组
【例2】如图,若直线l1与l2相交于点P,则根据图象可得,二
元一次方程组 的解是________.【解题探究】1.二元一次方程2x-y=3与一次函数y=2x-3有什么关系?
提示:这条直线y=2x-3上每个点的坐标(x,y)都是这个二元一次方程2x-y=3的解.
2.二元一次方程 x+y=3与一次函数y=-x+3有什么关系?
提示:这条直线y=-x+3上每个点的坐标(x,y)都是这个二元一次方程x+y=3的解.3.方程组 与一次函数y=2x-3和一次函数y=-x+3有
什么关系?
提示:这两条直线的交点的坐标(x,y)就是方程组
的解.
4.直线y=2x-3和直线y=-x+3的交点为_______,所以方程组
的解为________(2,1)【总结提升】用图象法确定二元一次方程组的解
(1)将两个方程都化为y=kx+b(k,b是常数,k≠0)的形式.
(2)画出两个函数的图象,确定交点坐标.
(3)两个一次函数图象交点的坐标是这个二元一次方程组的解.题组一:用函数图象的方法解不等式
1.(2013·娄底中考)一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( )
A.x<0 B.x>0 C.x<2 D.x>2【解析】选C.y>0对应一次函数图象在x轴上方,自变量的范围是x<2.2.(2013·铜仁中考)如图,直线y=kx+b交坐标
轴于A(-2,0),B(0,3)两点,则不等式kx+b>0的
解集是( )
A.x>3 B.-2
【解析】选D.由函数图象可知,y=kx+b交x轴于(-2,0),
所以当x>-2时,y>0,即kx+b>0.3.如图,函数y=ax-1的图象过点(1,2),则
不等式ax-1>2的解集是 .
【解析】根据图象可知:y=ax-1>2的x的
取值范围是x>1,
即不等式ax-1>2的解集是x>1.
答案:x>14.如图,直线l1:y=x+1与直线l2:y=mx+n相
交于点P(a,2),则关于x的不等式x+1≥mx
+n的解集为 .
【解析】把y=2代入y=x+1,得x=1,
∴点P的坐标为(1,2),
根据图象可知当x≥1时,y=x+1的函数值大于y=mx+n相应的函数值.
因而不等式x+1≥mx+n的解集是:x≥1.
答案:x≥15.兄弟俩赛跑,开始前,弟弟在哥哥前方9m,已知弟弟每秒跑3m,哥哥每秒跑4m,列出函数关系式,画出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过100m?【解析】设兄弟俩赛跑的时间为x秒.哥哥跑过的路程为y1,弟弟跑过的路程为y2,根据题意,得y1=4x,y2=3x+9.函数图象如图:
从图象上来看:(1)当0
(3)弟弟先跑过20m,哥哥先跑过100m.题组二:用函数图象的方法解二元一次方程组
1.两条直线y=k1x+b1和y=k2x+b2相交于点A(-2,3),则方程组
的解是( )【解析】选B.∵两条直线y=k1x+b1和y=k2x+b2相交于点A(-2,
3),
∴x=-2,y=3就是方程组 的解.
∴方程组 的解为2.如图,以两条直线l1,l2的交点坐标为解的方程组是( )【解析】选C.直线l1经过(2,3),(0,-1),易知其函数解析式
为y=2x-1;直线l2经过(2,3),(0,1),易知其函数解析式为
y=x+1;因此以两条直线l1,l2的交点坐标为解的方程组可以
是:3.函数y=2x-3的图象上任意一点的坐标都一定满足二元一次方程:_________.
【解析】y=2x-3移项得2x-y-3=0.
答案:2x-y-3=04.如图,已知一次函数y=ax+b和正比例函数y=kx的图象交于点
P,则根据图象可得二元一次方程组 的解是_____.【解析】根据题意可知,二元一次方程组 的解就
是一次函数y=ax+b和正比例函数y=kx图象的交点P的坐标,由
一次函数y=ax+b和正比例函数y=kx的图象的交点为(-4,-2),
可得二元一次方程组 的解是
答案:5.已知两直线y1=2x-3,y2=6-x,
(1)在同一坐标系中作出它们的图象.
(2)求它们的交点A的坐标.
(3)根据图象指出x为何值时,y1>y2;x为何值时,y1
∴A(3,3).
(3)当x>3时,y1>y2;当x<3时,y1
则【想一想错在哪?】当自变量x满足什么条件时,一次函数
y=-2x+4的值满足y>-2?
提示:读图不认真,x>2时,对应的函数值在x轴下方,即y<0.
