20.2数据的波动程度(实例均为2013中考教师讲解典型题)课件 新人教版
文档属性
| 名称 | 20.2数据的波动程度(实例均为2013中考教师讲解典型题)课件 新人教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 771.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-17 00:00:00 | ||
图片预览











文档简介
课件31张PPT。数据的波动程度
第2课时1.进一步体会刻画数据离散程度的意义.(难点)
2.会通过计算数据的方差,决策生活实际问题.(重点、难点)
3.体会样本与总体关系,知道可以通过样本方差推断总体方差.方差与生活决策问题
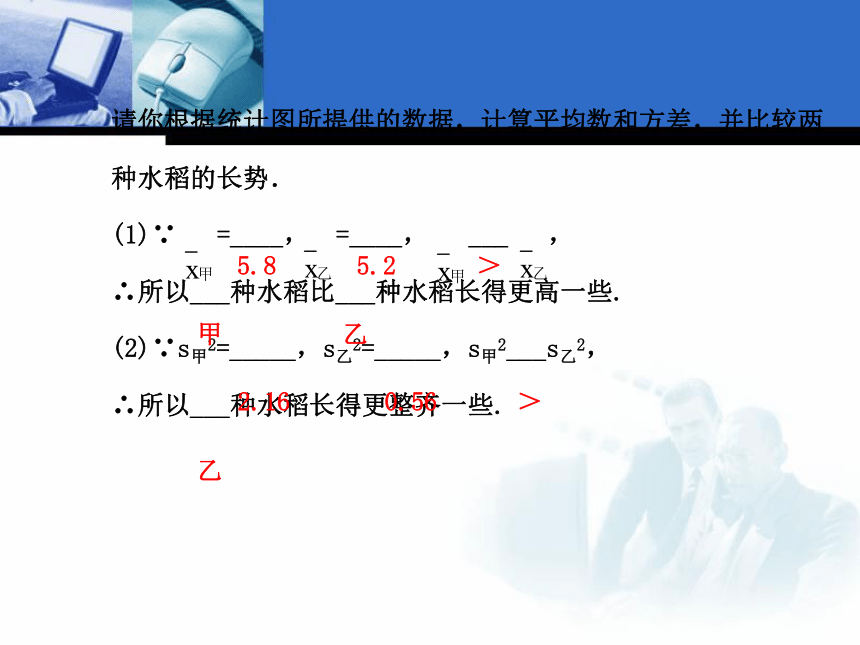
水稻种植是某市的传统农业.为了比较甲、乙两种水稻的长势,农技人员从两块试验田中,分别随机抽取5棵植株,将测得的苗高数据绘制成下图:请你根据统计图所提供的数据,计算平均数和方差,并比较两种水稻的长势.
(1)∵ =____, =____, ___ ,
∴所以___种水稻比___种水稻长得更高一些.
(2)∵s甲2=_____,s乙2=_____,s甲2___s乙2,
∴所以___种水稻长得更整齐一些.5.85.2>甲乙2.160.56>乙【总结】一般对于两组数据来说,可从平均数和方差两个方面
进行比较,平均数反映一组数据的_________,方差则反映一
组数据在平均数左右的_________,因此从平均数看或从方差
看,各有长处.一般水平波动大小 (打“√”或“×”)
(1)学习成绩方差越大,波动越大,成绩越差.( )
(2)若甲组数据的方差s甲2=0.39,乙组数据的方差s乙2=0.25,
则甲组数据比乙组数据大.( )
(3)两组数据中平均数与中位数都较大的一组,方差也较大.
( )
(4)若甲组数据的方差s甲2=0.1,乙组数据的方差s乙2=0.01,
则甲组数据比乙组数据稳定.( )××××(5)10块试验田得到两组不同品种的水稻产量数据,若平均亩
产量相等,则方差小的品种好.( )√知识点 方差的实际应用?
【例】为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据见表格和统计图:根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为谁的成绩好些?
(2)计算出sB2的大小,考虑平均数与方差,说明谁的成绩好些.
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参加竞赛较合适?说明你的理由.【思路点拨】(1)根据平均数与完全符合要求的个数两个量比较,平均数相等,完全符合要求的个数多的成绩好.
(2)根据平均数与方差两个量比较,平均数相等,方差小的成绩好.
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况时,要考虑谁的走势逐渐趋于稳定,即谁的潜力更大.【自主解答】(1)由于A与B的平均数都是20,但B完全符合要求
的个数比A多,所以B的成绩要好些.
(2)由统计图可知sB2= [5(20-20)2+3(19.9-20)2+(20.1-
20)2+(20.2-20)2]=0.008,而sA2=0.026,此时有sA2>
sB2,所以B的波动性小,即B的成绩较好.
(3)派A去参赛较合适.
理由:从图中折线走势可知,尽管A的成绩前面起伏较大,但
后来逐渐稳定,误差小,预测A的潜力大,可选派A去参赛更容
易取得好成绩.【总结提升】方差的两个应用
(1)衡量一组数据的波动情况:当两组数据的平均数相等或接近时,用方差来考察数据的有关特征,方差小的较稳定.
(2)用样本方差估计总体方差:考察总体方差时,如果所要考察的总体有许多个体,或考察本身有破坏性,实际中常用样本方差近似地估计总体方差.题组:方差的实际应用
1.(2013·重庆中考)为了比较甲、乙两种水稻秧苗谁出苗更整齐,每种秧苗各随机抽取50株,分别量出每株长度,发现两组秧苗的平均长度一样,甲、乙的方差分别是3.5,10.9,则下列说法正确的是( )A.甲秧苗出苗更整齐
B.乙秧苗出苗更整齐
C.甲、乙出苗一样整齐
D.无法确定甲、乙出苗谁更整齐
【解析】选A.因为甲、乙两种秧苗各随机抽取50株,发现两组秧苗的平均长度一样,并且甲、乙的方差分别是3.5,10.9,甲的方差较小,所以甲秧苗出苗更整齐.2.样本方差的作用是( )
A.用来估计总体的数值大小
B.用来估计样本的数值大小
C.用来衡量样本容量的大小
D.用来衡量样本的波动大小,估计总体的波动大小
【解析】选D.方差是反映一组数据的波动大小的一个量,因此样本方差的作用是用来衡量样本的波动大小,估计总体的波动大小.3.同班的两名学生在一学年里各次的数学考试成绩的平均分相
等,但他们的方差不相等,能正确评价他俩的数学学习情况的是
( )
A.学习水平一样
B.方差大的学生说明潜力大
C.方差较小的学生成绩较稳定
D.方差较小的学生成绩不稳定【解析】选C.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.4.某电器集团营销点自去年12月份至今年5月份销售两种不同品牌冰箱的数量如图,则下列说法正确的是( )A.甲品牌销售量较稳定
B.乙品牌销售量较稳定
C.甲、乙品牌销售量一样稳定
D.不能确定哪种品牌销售量稳定【解析】选B.读图可得甲品牌的平均数为(7+10+8+10+12+13)
÷6=10,乙品牌的平均数为(9+10+11+9+12+9)÷6=10,故
由于s甲2>s乙2,则销售量较稳定的是乙.5.(2012·咸宁中考)某班团支部统计了该班甲、乙、丙、丁四
名同学在5月份“书香校园”活动中的课外阅读时间,他们平
均每天课外阅读时间 与方差s2如表所示,你认为表现最好
的是( )
A.甲 B.乙 C.丙 D.丁【解析】选C.因为乙、丙的平均数大于甲、丁的平均数,故
乙、丙表现较好,又因丙的方差小于乙的方差,则丙的表现比
较稳定,所以丙的表现最好.6.某市统计局网站消息:我市实施了一系列增加居民收入的政策,确保了市区城镇居民收入水平保持增长.2010年到2013年,我市城镇居民人均可支配收入分别为:19027元、21689元、
24104元、26864元.某报评论说,这4年的年度人均可支配收入增长相当平稳.从统计学的角度看,“增长率相当平稳”说明这组数据增长率的( )比较小.( )
A.中位数 B.平均数
C.众数 D.方差【解析】选D.由“增长率相当平稳”说明这组数据的波动较小,从统计学的角度看,这组数据增长率的方差比较小.7.对人数相同的甲、乙两个班级的学生进行一次数学能力测试,统计出方差的大小关系是:s甲2>s乙2,由此可知这次测试结果( )
A.甲班成绩好 B.乙班成绩好
C.两班成绩一样好 D.无法确定
【解析】选D.由于方差的大小只反映数据的波动大小,故无法体现整体水平的高低.8.因业务扩大,拉巴新购置了甲、乙、丙三台牛肉干包装机分装质量相同的牛肉干,现从它们各自已经分装好的牛肉干包中随机抽取了10包,测得它们实际质量的方差分别为s甲2=0.55,s乙2=0.27,s丙2=0.31.可以确定____牛肉干包装机的质量最稳定.(填甲、乙、丙中的一个)
【解析】∵s甲2=0.55,s乙2=0.27,s丙2=0.31,∴s甲2>s丙2>
s乙2,∴质量最稳定的是乙.
答案:乙9.今年5月甲、乙两种股票连续10天开盘价格如下:(单位:元)
则在10天中,甲、乙两种股票波动较大的是 .
【解析】甲的方差约为0.011;乙的方差约为0.029,比较可得:乙的方差较大,故乙种股票波动较大.
答案:乙10.在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统
计表和扇形统计图如下:
(1)根据提供的信息,补全统计表及扇形统计图.
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如
果只能选一人参加比赛,你认为应该派谁去?并说明理由.
(参考资料:s2= )【解析】(1)补全统计表及扇形统计图如下表及图所示:
(2)应该派甲去.
理由: (10×4+9×3+8×2+7×1)=9(环).
s甲2= [4×(10-9)2+3×(9-9)2+2×(8-9)2+1×(7-9)2]=1.
因为甲、乙两人的平均成绩相同,而s甲2<s乙2,说明甲的成绩
比乙稳定.所以应派甲去.【想一想错在哪?】某校九年级上学期期末统一考试后,甲、乙两班的数学成绩(单位:分)统计情况如下表所示:
从各统计指标综合来看,你认为哪个班的成绩较好?为什么?提示:方差是反映一组数据波动大小的量,在平均数相等或相近时,可以作为评价成绩是否稳定的标准,而不能作为评价成绩好坏的标准.
第2课时1.进一步体会刻画数据离散程度的意义.(难点)
2.会通过计算数据的方差,决策生活实际问题.(重点、难点)
3.体会样本与总体关系,知道可以通过样本方差推断总体方差.方差与生活决策问题
水稻种植是某市的传统农业.为了比较甲、乙两种水稻的长势,农技人员从两块试验田中,分别随机抽取5棵植株,将测得的苗高数据绘制成下图:请你根据统计图所提供的数据,计算平均数和方差,并比较两种水稻的长势.
(1)∵ =____, =____, ___ ,
∴所以___种水稻比___种水稻长得更高一些.
(2)∵s甲2=_____,s乙2=_____,s甲2___s乙2,
∴所以___种水稻长得更整齐一些.5.85.2>甲乙2.160.56>乙【总结】一般对于两组数据来说,可从平均数和方差两个方面
进行比较,平均数反映一组数据的_________,方差则反映一
组数据在平均数左右的_________,因此从平均数看或从方差
看,各有长处.一般水平波动大小 (打“√”或“×”)
(1)学习成绩方差越大,波动越大,成绩越差.( )
(2)若甲组数据的方差s甲2=0.39,乙组数据的方差s乙2=0.25,
则甲组数据比乙组数据大.( )
(3)两组数据中平均数与中位数都较大的一组,方差也较大.
( )
(4)若甲组数据的方差s甲2=0.1,乙组数据的方差s乙2=0.01,
则甲组数据比乙组数据稳定.( )××××(5)10块试验田得到两组不同品种的水稻产量数据,若平均亩
产量相等,则方差小的品种好.( )√知识点 方差的实际应用?
【例】为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据见表格和统计图:根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为谁的成绩好些?
(2)计算出sB2的大小,考虑平均数与方差,说明谁的成绩好些.
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参加竞赛较合适?说明你的理由.【思路点拨】(1)根据平均数与完全符合要求的个数两个量比较,平均数相等,完全符合要求的个数多的成绩好.
(2)根据平均数与方差两个量比较,平均数相等,方差小的成绩好.
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况时,要考虑谁的走势逐渐趋于稳定,即谁的潜力更大.【自主解答】(1)由于A与B的平均数都是20,但B完全符合要求
的个数比A多,所以B的成绩要好些.
(2)由统计图可知sB2= [5(20-20)2+3(19.9-20)2+(20.1-
20)2+(20.2-20)2]=0.008,而sA2=0.026,此时有sA2>
sB2,所以B的波动性小,即B的成绩较好.
(3)派A去参赛较合适.
理由:从图中折线走势可知,尽管A的成绩前面起伏较大,但
后来逐渐稳定,误差小,预测A的潜力大,可选派A去参赛更容
易取得好成绩.【总结提升】方差的两个应用
(1)衡量一组数据的波动情况:当两组数据的平均数相等或接近时,用方差来考察数据的有关特征,方差小的较稳定.
(2)用样本方差估计总体方差:考察总体方差时,如果所要考察的总体有许多个体,或考察本身有破坏性,实际中常用样本方差近似地估计总体方差.题组:方差的实际应用
1.(2013·重庆中考)为了比较甲、乙两种水稻秧苗谁出苗更整齐,每种秧苗各随机抽取50株,分别量出每株长度,发现两组秧苗的平均长度一样,甲、乙的方差分别是3.5,10.9,则下列说法正确的是( )A.甲秧苗出苗更整齐
B.乙秧苗出苗更整齐
C.甲、乙出苗一样整齐
D.无法确定甲、乙出苗谁更整齐
【解析】选A.因为甲、乙两种秧苗各随机抽取50株,发现两组秧苗的平均长度一样,并且甲、乙的方差分别是3.5,10.9,甲的方差较小,所以甲秧苗出苗更整齐.2.样本方差的作用是( )
A.用来估计总体的数值大小
B.用来估计样本的数值大小
C.用来衡量样本容量的大小
D.用来衡量样本的波动大小,估计总体的波动大小
【解析】选D.方差是反映一组数据的波动大小的一个量,因此样本方差的作用是用来衡量样本的波动大小,估计总体的波动大小.3.同班的两名学生在一学年里各次的数学考试成绩的平均分相
等,但他们的方差不相等,能正确评价他俩的数学学习情况的是
( )
A.学习水平一样
B.方差大的学生说明潜力大
C.方差较小的学生成绩较稳定
D.方差较小的学生成绩不稳定【解析】选C.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.4.某电器集团营销点自去年12月份至今年5月份销售两种不同品牌冰箱的数量如图,则下列说法正确的是( )A.甲品牌销售量较稳定
B.乙品牌销售量较稳定
C.甲、乙品牌销售量一样稳定
D.不能确定哪种品牌销售量稳定【解析】选B.读图可得甲品牌的平均数为(7+10+8+10+12+13)
÷6=10,乙品牌的平均数为(9+10+11+9+12+9)÷6=10,故
由于s甲2>s乙2,则销售量较稳定的是乙.5.(2012·咸宁中考)某班团支部统计了该班甲、乙、丙、丁四
名同学在5月份“书香校园”活动中的课外阅读时间,他们平
均每天课外阅读时间 与方差s2如表所示,你认为表现最好
的是( )
A.甲 B.乙 C.丙 D.丁【解析】选C.因为乙、丙的平均数大于甲、丁的平均数,故
乙、丙表现较好,又因丙的方差小于乙的方差,则丙的表现比
较稳定,所以丙的表现最好.6.某市统计局网站消息:我市实施了一系列增加居民收入的政策,确保了市区城镇居民收入水平保持增长.2010年到2013年,我市城镇居民人均可支配收入分别为:19027元、21689元、
24104元、26864元.某报评论说,这4年的年度人均可支配收入增长相当平稳.从统计学的角度看,“增长率相当平稳”说明这组数据增长率的( )比较小.( )
A.中位数 B.平均数
C.众数 D.方差【解析】选D.由“增长率相当平稳”说明这组数据的波动较小,从统计学的角度看,这组数据增长率的方差比较小.7.对人数相同的甲、乙两个班级的学生进行一次数学能力测试,统计出方差的大小关系是:s甲2>s乙2,由此可知这次测试结果( )
A.甲班成绩好 B.乙班成绩好
C.两班成绩一样好 D.无法确定
【解析】选D.由于方差的大小只反映数据的波动大小,故无法体现整体水平的高低.8.因业务扩大,拉巴新购置了甲、乙、丙三台牛肉干包装机分装质量相同的牛肉干,现从它们各自已经分装好的牛肉干包中随机抽取了10包,测得它们实际质量的方差分别为s甲2=0.55,s乙2=0.27,s丙2=0.31.可以确定____牛肉干包装机的质量最稳定.(填甲、乙、丙中的一个)
【解析】∵s甲2=0.55,s乙2=0.27,s丙2=0.31,∴s甲2>s丙2>
s乙2,∴质量最稳定的是乙.
答案:乙9.今年5月甲、乙两种股票连续10天开盘价格如下:(单位:元)
则在10天中,甲、乙两种股票波动较大的是 .
【解析】甲的方差约为0.011;乙的方差约为0.029,比较可得:乙的方差较大,故乙种股票波动较大.
答案:乙10.在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统
计表和扇形统计图如下:
(1)根据提供的信息,补全统计表及扇形统计图.
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如
果只能选一人参加比赛,你认为应该派谁去?并说明理由.
(参考资料:s2= )【解析】(1)补全统计表及扇形统计图如下表及图所示:
(2)应该派甲去.
理由: (10×4+9×3+8×2+7×1)=9(环).
s甲2= [4×(10-9)2+3×(9-9)2+2×(8-9)2+1×(7-9)2]=1.
因为甲、乙两人的平均成绩相同,而s甲2<s乙2,说明甲的成绩
比乙稳定.所以应派甲去.【想一想错在哪?】某校九年级上学期期末统一考试后,甲、乙两班的数学成绩(单位:分)统计情况如下表所示:
从各统计指标综合来看,你认为哪个班的成绩较好?为什么?提示:方差是反映一组数据波动大小的量,在平均数相等或相近时,可以作为评价成绩是否稳定的标准,而不能作为评价成绩好坏的标准.
