物理人教版(2019)必修第二册7.3万有引力理论的成就(共16张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册7.3万有引力理论的成就(共16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-11 18:13:34 | ||
图片预览






文档简介
(共16张PPT)
万有引力理论的成就
怎样称量地球的质量呢?
计算天体质量
方法一:重力加速度法(g、R)
算一算:设地面附近的重力加速度g=9.8m/s2,地球半径R =6.4×106m,引力常量G=6.67×10-11 N·m2/kg2,试估算地球的质量。
卡文迪什被称为“第一个称量地球质量的人”!
GM=gR2(黄金代换式)
GM=gR2
若不考虑地球自转的影响
计算天体质量
算一算:已知月球绕地球周期T=27.3天,月地平均距离r=3.84×108m,引力常量G=6.67×10-11 N·m2/kg2,试估算地球的质量。
方法二:环绕法(T、r)
计算天体质量
★需要记忆的公式:球的体积计算公式:
物体的密度计算公式:
计算天体密度
解题思路:
1、不考虑天体自转,天体表面物体所受万有引力等于重力(重力加速度法)
2、环绕天体做匀速圆周运动所受万有引力提供向心力
(环绕法)
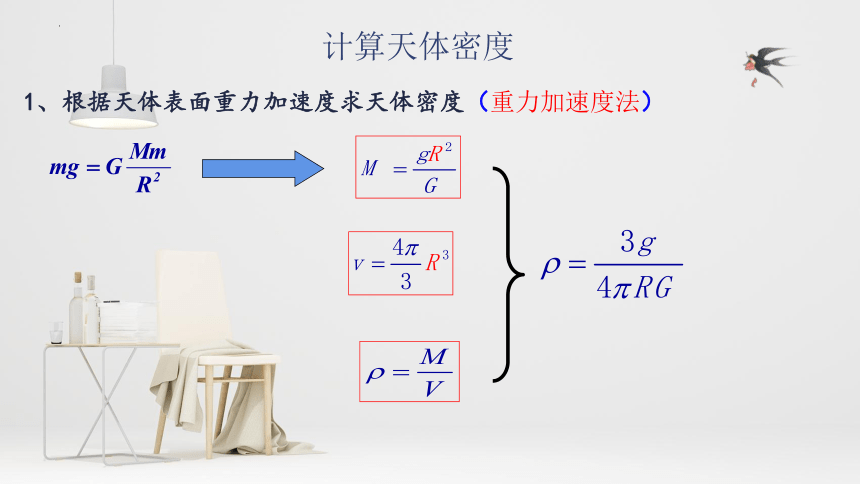
1、根据天体表面重力加速度求天体密度(重力加速度法)
计算天体密度
2、利用环绕天体(如卫星)求天体密度(环绕法)
r≈R
当卫星环绕中心天体表面运动时
R
r
结论:当卫星环绕中心天体表面运动时,轨道半径r≈R,则此中心天体的密度为:
典例:设火星探测器在距离火星表面h高度做周期为T的匀速圆周运动。已知火星的半径为R,引力常量为G。求:
(1)探测到的火星质量;
(2)探测到的火星表面的重力加速度;
(3)探测到的火星的密度。
典例:假设航天员登月后,站在月球表面沿水平方向以初速度v0抛出一个小球,经时间t落地,落地时速度与水平地面间的夹角为α,已知月球半径为R,引力常量为G,求:
(1)月球表面的重力加速度g;
(2)月球的质量m月;
(3)月球的密度ρ。
在18世纪发现的第七个行星——天王星的运动轨道,总是同根据万有引力定律计算出来的有一定偏离.当时有人预测,肯定在其轨道外还有一颗未发现的新星. 英国亚当斯和法国勒维烈各自独立地利用万有引力定律计算出这颗“新行星”的轨道.后来, 1846年9月23日由德国的伽勒发现了海王星。
海王星 笔尖下发现的行星
发现未知天体
(英)亚当斯 (法)勒维耶
海王星发现之后,人们发现它的轨道也与理论计算的不一致。于是几位学者用亚当斯和勒维耶列的方法预言另一颗行星的存在。
在预言提出之后,1930年3月14日,汤博发现了这颗行星——冥王星。
发现未知天体
哈雷依据万有引力定律,用一年时间计算了它们的轨道。发现 1531 年、1607 年和 1682 年出现的这三颗彗星轨道看起来如出一辙,他大胆预言,这三次出现的彗星是同一颗星(图 7.3-3),周期约为 76 年,并预言它将于 1758 年底或 1759 年初再次回归。1759 年 3 月这颗彗星如期通过了近日点,它最近一次回归是 1986 年,它的下次回归将在2061 年左右。
预言哈雷彗星回归
天体运动的分析与计算
天体运动的线速度、角速度、周期、向心加速度与半径关系如何?
在地球表面,忽略自转
黄金代换公式
典例:如图1所示,a、b是两颗绕地球做匀速圆周运动的人造地球卫星,它们距地面的高度分别是R和2R(R为地球半径).求两卫星的线速度、角速度、周期之比?
图1
解析 两卫星均做匀速圆周运动,则有F万=F向
由
得
由
得
由
得
结
束
万有引力理论的成就
怎样称量地球的质量呢?
计算天体质量
方法一:重力加速度法(g、R)
算一算:设地面附近的重力加速度g=9.8m/s2,地球半径R =6.4×106m,引力常量G=6.67×10-11 N·m2/kg2,试估算地球的质量。
卡文迪什被称为“第一个称量地球质量的人”!
GM=gR2(黄金代换式)
GM=gR2
若不考虑地球自转的影响
计算天体质量
算一算:已知月球绕地球周期T=27.3天,月地平均距离r=3.84×108m,引力常量G=6.67×10-11 N·m2/kg2,试估算地球的质量。
方法二:环绕法(T、r)
计算天体质量
★需要记忆的公式:球的体积计算公式:
物体的密度计算公式:
计算天体密度
解题思路:
1、不考虑天体自转,天体表面物体所受万有引力等于重力(重力加速度法)
2、环绕天体做匀速圆周运动所受万有引力提供向心力
(环绕法)
1、根据天体表面重力加速度求天体密度(重力加速度法)
计算天体密度
2、利用环绕天体(如卫星)求天体密度(环绕法)
r≈R
当卫星环绕中心天体表面运动时
R
r
结论:当卫星环绕中心天体表面运动时,轨道半径r≈R,则此中心天体的密度为:
典例:设火星探测器在距离火星表面h高度做周期为T的匀速圆周运动。已知火星的半径为R,引力常量为G。求:
(1)探测到的火星质量;
(2)探测到的火星表面的重力加速度;
(3)探测到的火星的密度。
典例:假设航天员登月后,站在月球表面沿水平方向以初速度v0抛出一个小球,经时间t落地,落地时速度与水平地面间的夹角为α,已知月球半径为R,引力常量为G,求:
(1)月球表面的重力加速度g;
(2)月球的质量m月;
(3)月球的密度ρ。
在18世纪发现的第七个行星——天王星的运动轨道,总是同根据万有引力定律计算出来的有一定偏离.当时有人预测,肯定在其轨道外还有一颗未发现的新星. 英国亚当斯和法国勒维烈各自独立地利用万有引力定律计算出这颗“新行星”的轨道.后来, 1846年9月23日由德国的伽勒发现了海王星。
海王星 笔尖下发现的行星
发现未知天体
(英)亚当斯 (法)勒维耶
海王星发现之后,人们发现它的轨道也与理论计算的不一致。于是几位学者用亚当斯和勒维耶列的方法预言另一颗行星的存在。
在预言提出之后,1930年3月14日,汤博发现了这颗行星——冥王星。
发现未知天体
哈雷依据万有引力定律,用一年时间计算了它们的轨道。发现 1531 年、1607 年和 1682 年出现的这三颗彗星轨道看起来如出一辙,他大胆预言,这三次出现的彗星是同一颗星(图 7.3-3),周期约为 76 年,并预言它将于 1758 年底或 1759 年初再次回归。1759 年 3 月这颗彗星如期通过了近日点,它最近一次回归是 1986 年,它的下次回归将在2061 年左右。
预言哈雷彗星回归
天体运动的分析与计算
天体运动的线速度、角速度、周期、向心加速度与半径关系如何?
在地球表面,忽略自转
黄金代换公式
典例:如图1所示,a、b是两颗绕地球做匀速圆周运动的人造地球卫星,它们距地面的高度分别是R和2R(R为地球半径).求两卫星的线速度、角速度、周期之比?
图1
解析 两卫星均做匀速圆周运动,则有F万=F向
由
得
由
得
由
得
结
束
