新课标北师大版四下5.3《方程》课件(32张PPT)
文档属性
| 名称 | 新课标北师大版四下5.3《方程》课件(32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 14:27:09 | ||
图片预览








文档简介
(共32张PPT)
方程
北师大版四年级下册
教学目标
1.学习目标描述:借助天平的平衡关系,理解方程的意义,了解方程与等式的关系,会用方程表示生活情境中简单的数量关系。
2.学习内容分析:本节课是在学生已经学过用字母表示数的基础上展开的,为下面等式的性质和解方程的教学作铺垫,有着承前启后的重要作用。方程是表示等量关系的一种模式,学习方程最重要的方面是能够根据具体问题中的数量关系,找出等量关系列出方程。教材编排时,创设了多方面的问题情境,使学生通过对多个实例的讨论,
教学目标
发现了方程能刻画现实生活中的很多问题,从而体会到方程的作用,并产生积极的学习愿望,这对于学生学习方程起了重要的作用。
3.学科核心素养分析:经历将现实问题抽象成等式与方程的过程,积累将等量关系符号化的活动经验。在丰富的问题情境中感受生活中存在大量的等量关系,体验数学与生活的密切联系。
新知导入
看图写出等量关系。
100g
一只小狗的重量=两只小猫的重量
一个石榴的总量=100g
新知导入
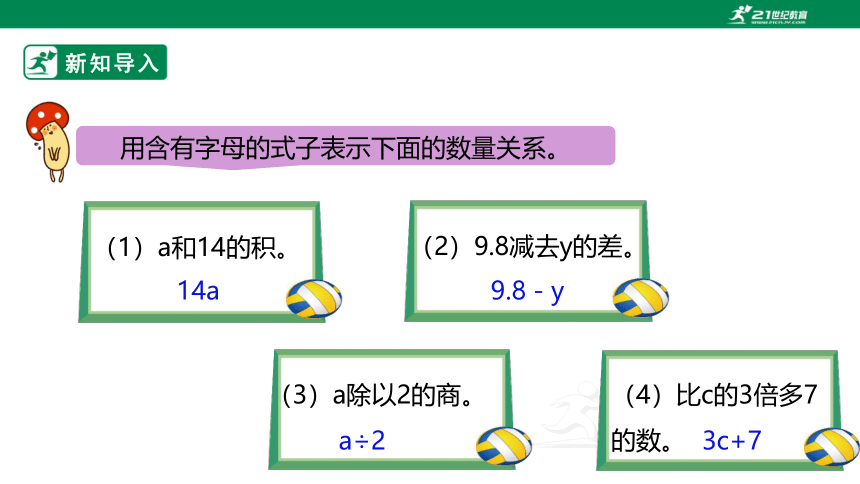
用含有字母的式子表示下面的数量关系。
(1)a和14的积。
(2)9.8减去y的差。
(3)a除以2的商。
(4)比c的3倍多7的数。
14a
9.8-y
a÷2
3c+7
新知导入
玩跷跷板的时候,如果两边的重量不一样,重的一边就会把轻的一边翘起来;当两边的重量相等时,跷跷板就平衡了。
新知讲解
10g
2g
指针在中间
天平正好平衡
说明天平两边一样重。
10g=樱桃的质量+2g
新知讲解
说一说下面各图中的等量关系。
每盒种子的质量×4=2000g
2000毫升=每个热水瓶盛水量×2+200毫升
新知讲解
思考:
如果用未知数x来表示樱桃的质量,你能用式子表示天平中的等量关系?
10g
2g
10g=樱桃的质量+2g
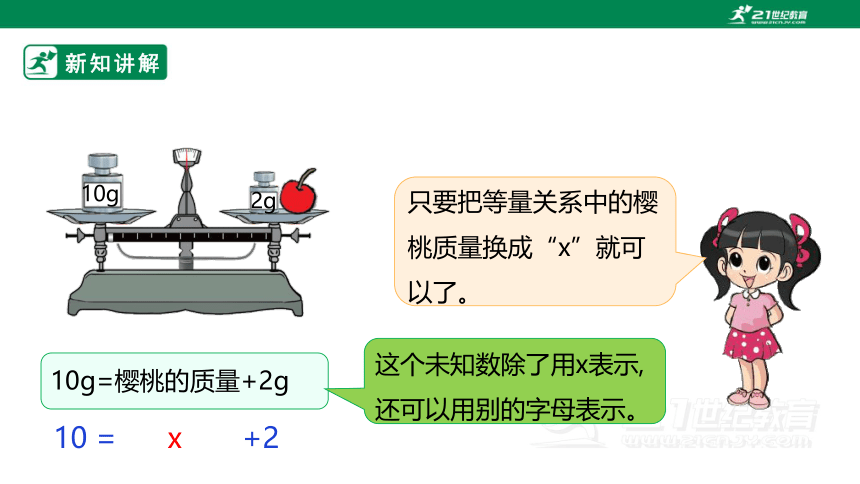
新知讲解
10g
2g
10g=樱桃的质量+2g
只要把等量关系中的樱桃质量换成“x”就可以了。
10 = x +2
这个未知数除了用x表示,还可以用别的字母表示。
新知讲解
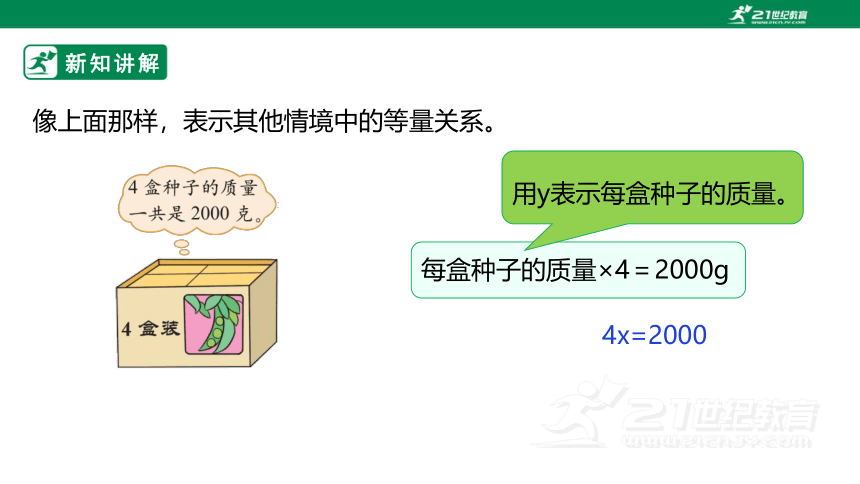
像上面那样,表示其他情境中的等量关系。
每盒种子的质量×4=2000g
用y表示每盒种子的质量。
4x=2000
新知讲解
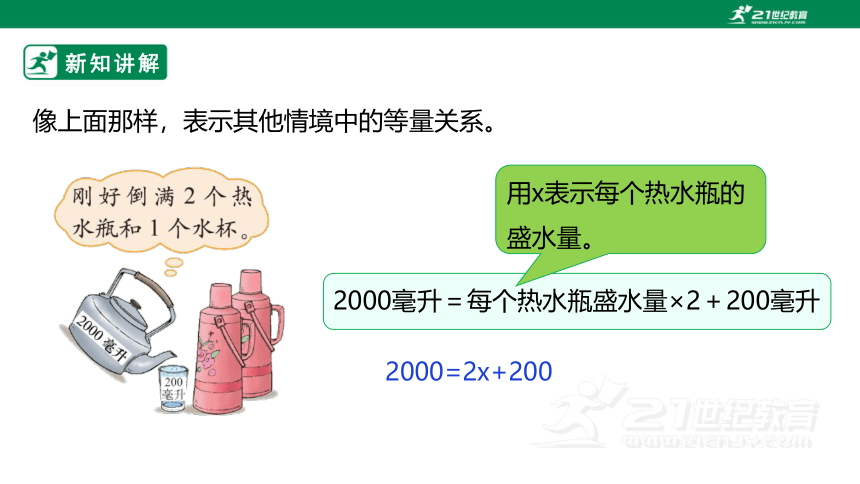
像上面那样,表示其他情境中的等量关系。
2000毫升=每个热水瓶盛水量×2+200毫升
用x表示每个热水瓶的盛水量。
2000=2x+200
新知讲解
10=x+2
4y=2000
2000=2z+200
像这样左右两边相等的式子,我们把它叫做等式。
思考:
观察左面的等式,它们有什么共同点?与同伴进行交流。
新知讲解
10=x+2
4y=2000
2000=2z+200
这三个等式都含有未知数。
像10=x+2,4y=2000,…这样含有未知数的等式叫做方程。
新知讲解
方程必须具备两个条件:(1)必须是等式;(2)必须含有未知数。
新知讲解
你知道吗?
公元250年前后,古希腊数学家丢番图写了一本数学巨著《算术》,引入了未知数的概念,并使用符号表示未知数,这是数学史上的一个重要事件,开启了符号代数的大门。因此,人们常常称丢番图为“代数学之父”。
新知讲解
50+50=100
是等式但不是方程
50+x=100
是等式也是方程
所有的方程都是等式,所有的等式不一定是方程。
等式
方程
课堂练习
选一选。
方程
3x
7x=35
5<z
课堂练习
选一选。
方程
x=7
4+9=14
7+a
课堂练习
选一选。
方程
3+4<a
8a
32-a=15
课堂练习
选一选。
等式
6>a
8=y
65÷x
课堂练习
判断。
含有未知数的式子是方程。
对
错
课堂练习
判断。
所有的方程都是等式,但所有的等式不一定都是方程。
对
错
课堂练习
判断。
x-13=24是方程,但不是等式。
对
错
课堂练习
判断。
x=0不是方程。
对
错
360g
课堂练习
看图列出方程。
C=48厘米
16厘米
y厘米
xg
xg
xg
(16+y)×2=48
3x=360
课堂练习
4.拓展应用:某工厂有女职工x人,男职工432人,男职工人数比女职工人数的2倍还多32人,女职工有多少人 (只列方程)
女职工人数×2+32=男职工人数
2x+32=432
先写出等量关系。
课堂总结
通过今天的学习,你有哪些收获?
我知道了含有未知数的等式是方程。
我还能根据等量关系列出方程了。
板书设计
方程
10g=樱桃的质量+2g 10=x+2
每盒种子的质量×4=2000g 4y=2000
2000毫升=每个热水瓶盛水量×2+200毫升 2000=2z+200
含有未知数的等式是方程。
作业布置
完成“练一练”第1~2题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
方程
北师大版四年级下册
教学目标
1.学习目标描述:借助天平的平衡关系,理解方程的意义,了解方程与等式的关系,会用方程表示生活情境中简单的数量关系。
2.学习内容分析:本节课是在学生已经学过用字母表示数的基础上展开的,为下面等式的性质和解方程的教学作铺垫,有着承前启后的重要作用。方程是表示等量关系的一种模式,学习方程最重要的方面是能够根据具体问题中的数量关系,找出等量关系列出方程。教材编排时,创设了多方面的问题情境,使学生通过对多个实例的讨论,
教学目标
发现了方程能刻画现实生活中的很多问题,从而体会到方程的作用,并产生积极的学习愿望,这对于学生学习方程起了重要的作用。
3.学科核心素养分析:经历将现实问题抽象成等式与方程的过程,积累将等量关系符号化的活动经验。在丰富的问题情境中感受生活中存在大量的等量关系,体验数学与生活的密切联系。
新知导入
看图写出等量关系。
100g
一只小狗的重量=两只小猫的重量
一个石榴的总量=100g
新知导入
用含有字母的式子表示下面的数量关系。
(1)a和14的积。
(2)9.8减去y的差。
(3)a除以2的商。
(4)比c的3倍多7的数。
14a
9.8-y
a÷2
3c+7
新知导入
玩跷跷板的时候,如果两边的重量不一样,重的一边就会把轻的一边翘起来;当两边的重量相等时,跷跷板就平衡了。
新知讲解
10g
2g
指针在中间
天平正好平衡
说明天平两边一样重。
10g=樱桃的质量+2g
新知讲解
说一说下面各图中的等量关系。
每盒种子的质量×4=2000g
2000毫升=每个热水瓶盛水量×2+200毫升
新知讲解
思考:
如果用未知数x来表示樱桃的质量,你能用式子表示天平中的等量关系?
10g
2g
10g=樱桃的质量+2g
新知讲解
10g
2g
10g=樱桃的质量+2g
只要把等量关系中的樱桃质量换成“x”就可以了。
10 = x +2
这个未知数除了用x表示,还可以用别的字母表示。
新知讲解
像上面那样,表示其他情境中的等量关系。
每盒种子的质量×4=2000g
用y表示每盒种子的质量。
4x=2000
新知讲解
像上面那样,表示其他情境中的等量关系。
2000毫升=每个热水瓶盛水量×2+200毫升
用x表示每个热水瓶的盛水量。
2000=2x+200
新知讲解
10=x+2
4y=2000
2000=2z+200
像这样左右两边相等的式子,我们把它叫做等式。
思考:
观察左面的等式,它们有什么共同点?与同伴进行交流。
新知讲解
10=x+2
4y=2000
2000=2z+200
这三个等式都含有未知数。
像10=x+2,4y=2000,…这样含有未知数的等式叫做方程。
新知讲解
方程必须具备两个条件:(1)必须是等式;(2)必须含有未知数。
新知讲解
你知道吗?
公元250年前后,古希腊数学家丢番图写了一本数学巨著《算术》,引入了未知数的概念,并使用符号表示未知数,这是数学史上的一个重要事件,开启了符号代数的大门。因此,人们常常称丢番图为“代数学之父”。
新知讲解
50+50=100
是等式但不是方程
50+x=100
是等式也是方程
所有的方程都是等式,所有的等式不一定是方程。
等式
方程
课堂练习
选一选。
方程
3x
7x=35
5<z
课堂练习
选一选。
方程
x=7
4+9=14
7+a
课堂练习
选一选。
方程
3+4<a
8a
32-a=15
课堂练习
选一选。
等式
6>a
8=y
65÷x
课堂练习
判断。
含有未知数的式子是方程。
对
错
课堂练习
判断。
所有的方程都是等式,但所有的等式不一定都是方程。
对
错
课堂练习
判断。
x-13=24是方程,但不是等式。
对
错
课堂练习
判断。
x=0不是方程。
对
错
360g
课堂练习
看图列出方程。
C=48厘米
16厘米
y厘米
xg
xg
xg
(16+y)×2=48
3x=360
课堂练习
4.拓展应用:某工厂有女职工x人,男职工432人,男职工人数比女职工人数的2倍还多32人,女职工有多少人 (只列方程)
女职工人数×2+32=男职工人数
2x+32=432
先写出等量关系。
课堂总结
通过今天的学习,你有哪些收获?
我知道了含有未知数的等式是方程。
我还能根据等量关系列出方程了。
板书设计
方程
10g=樱桃的质量+2g 10=x+2
每盒种子的质量×4=2000g 4y=2000
2000毫升=每个热水瓶盛水量×2+200毫升 2000=2z+200
含有未知数的等式是方程。
作业布置
完成“练一练”第1~2题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
