第六单元 运算律(学生版+教师版) 2022-2023学年四年级数学下册单元复习讲义(苏教版含答案)
文档属性
| 名称 | 第六单元 运算律(学生版+教师版) 2022-2023学年四年级数学下册单元复习讲义(苏教版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 00:00:00 | ||
图片预览




文档简介
苏教版数学四年级下册
第六单元 运算律
知识点01:加法交换律
两个数相加,交换两个加数的位置,和不变。
用字母表示:a+b=b+a。
知识点02:加法结合律
三个数相加,先把前两个数相加,再与第三个数相加,或者先把后两个数相加再与第一个数相加,和不变。
2. 用字母表示 :(a+b)+c=a+(b+c)。
知识点03:加法运算律的应用
在连加算式中,当某些加数相加可以凑成整十、整百整千......数时,应用加法运算律可以使计算简便。
知识点04:乘法交换律
两个数相乘交换两个录数的位置积不变
用字母表示:a×b=b×a。
知识点05:乘法结合律
1.三个数相乘,先把前两个数相乘,再与第三个数相乘,或者先把后两个数相乘,再与第一个数相乘积不变。
2. 用字母表示:(a×b)×c=a×(b×c)。
知识点06:乘法分配律
两个数的和与一个数相乘,可以先把这两个数分别与这个数相乘再相加。
用字母表示:(a+b)×c=a×c+b×c。
知识点07:乘法运算律的应用
在连乘算式中,当某两个乘数的积正好是整十、整百整千...数时,应用乘法运算律可以使计算简便.
两个数相乘,如果有一个数接近整百数可以先将这个数转化成整百数加或减一个数的形式,再应用乘法分配律进行计算。
在求两积之和的算式中,如果乘法算式中有一个乘数相同,另外两个乘数相加可以凑成整十、整百、整千...数时,可以根据乘法分配律的逆运算来计算。
知识点08:解决问题
解决问题之前,可以先画图或列表整理题中的条件和问题,再从不同的角度去思考,就会得到不同的解题方法。
考点01:加法运算律
【典例分析01】想一想,填一填.
【分析】根据整数加法的计算法则计算并填空即可.
【解答】解:
【点评】这道题目考查的是整数加法,属于基础题目,要熟练掌握并计算.
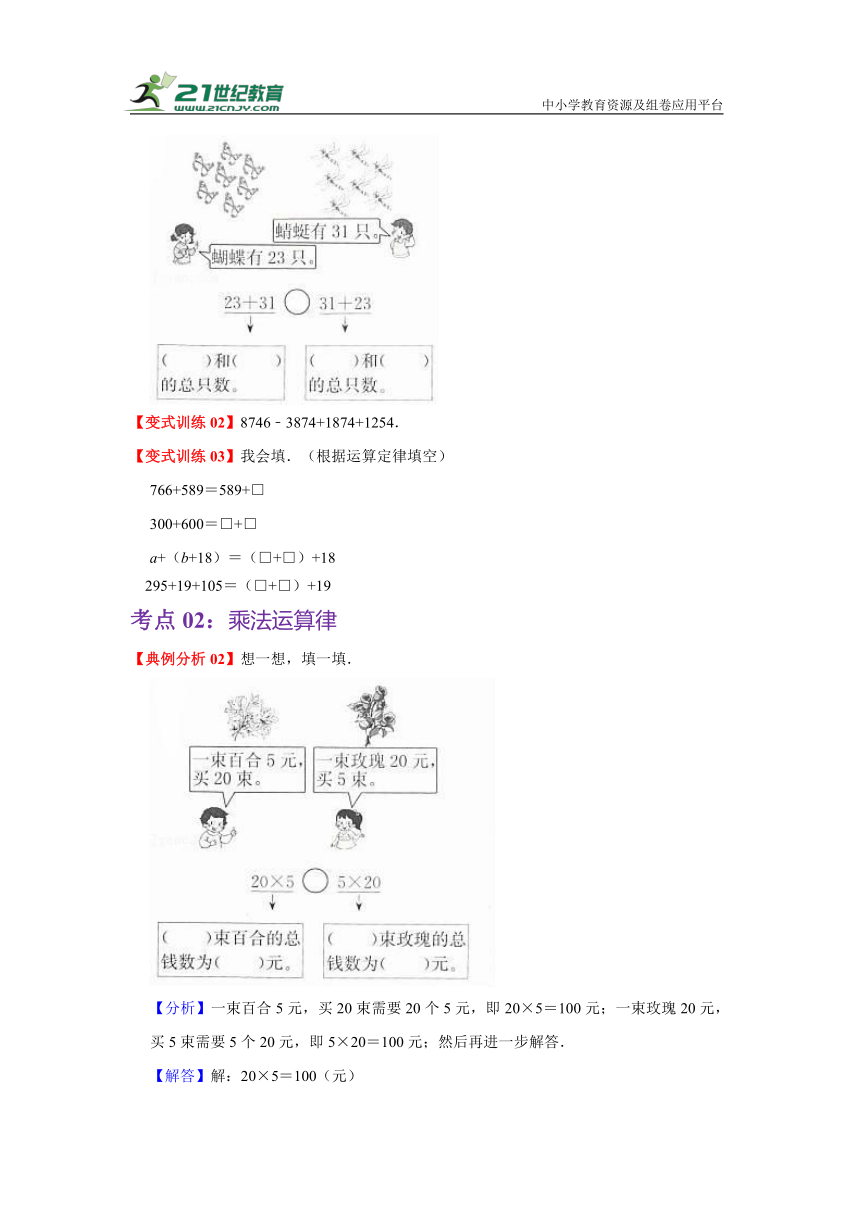
【变式训练01】想一想,填一填.
【变式训练02】8746﹣3874+1874+1254.
【变式训练03】我会填.(根据运算定律填空)
766+589=589+□
300+600=□+□
a+(b+18)=(□+□)+18
295+19+105=(□+□)+19
考点02:乘法运算律
【典例分析02】想一想,填一填.
【分析】一束百合5元,买20束需要20个5元,即20×5=100元;一束玫瑰20元,买5束需要5个20元,即5×20=100元;然后再进一步解答.
【解答】解:20×5=100(元)
表示20束百合的总钱数为100元;
5×20=100(元)
表示5束玫瑰的总钱数为100元;
所以,20×5=5×20.
故答案为:
.
【点评】考查了整数乘法的意义的灵活运用.
【变式训练01】你能很快说出每盏灯笼上三个数连加的和与三个数连乘的积吗?
【变式训练02】用4块同样大小的长方形木板拼成一个广告牌(如图),已知每块木板长25dm,宽16dm,新广告牌的面积是多少平方米?(用两种方法解答)
【变式训练03】《百科知识》每套125元,《数学王国》每套35元。学校各买了6套,一共花多少钱?
考点03:运算定律与简便运算
【典例分析03】计算417﹣198时,可以这样想:417﹣198=417﹣200+2=219,请你试着用这样的方法计算:621+198= 621+200﹣2 = 819 。
【分析】计算417﹣198时,可以这样想:417﹣198=417﹣200+2=219,这是运用凑整法,把198,看成整百数200,减去200就多减了2,再加上2;计算621+198时可以把198看成200,621加200比621加198多加了2,再减去2即可。
【解答】解:621+198
=621+200﹣2
=819
故答案为:621+200﹣2,819。
【点评】本题考查了运用凑整法计算整数加法、减法的方法,注意找清楚多加了几或者多减去了几。
【变式训练01】25× ×4=25× ×34
a×8﹣b× =〔a〇 〕×
【变式训练02】两个加数相加,交换加数的位置,和不变,这叫做加法交换律,用字母表示是a+b=b+a,请你像第3题的同学一样,用一种喜欢的方式表示加法交换律的意思。
【变式训练03】水果店运进28箱苹果和22箱梨,每箱苹果和梨都是25kg,这些苹果和梨一共多少千克?
一.选择题(共5小题)
1.(11+13+15+17+19)﹣(10+12+14+16+18)=( )
A.5 B.4 C.3 D.0
2.a+b+c+d=(a+d)+(b+c),这道算式运用了( )
A.加法交换律 B.加法结合律
C.加法交换律和结合律
3.计算125×18×8时,明明是按照125×8×18来算的,他这样算的依据是( )
A.乘法结合律 B.乘法分配律 C.乘法交换律
4.计算36×25时,这样计算:36×25=9×(4×25)=9×100=900,运用了( )
A.乘法交换律 B.乘法结合律 C.乘法分配律
5.102×47=(100+2)×47=100×47+2×47运用了( )
A.乘法交换律 B.乘法分配律 C.乘法结合律 D.加法结合律
二.填空题(共5小题)
6.a×b=b×a这个运算规律是 律.
7.根据加法结合律在横线上填上适当的数或字母。
a+(8+b)=( + )+b
8.已知△﹣□=80,那么35×△﹣35×□= 。
9.根据学过的运算律填一填。
(1)38×2×5=38×( ×5)
(2)(81+79)+21= +( +21)
10. +45= +82,这里运用了加法 ,用字母表示是 。
三.判断题(共5小题)
11.85×48+85×52=85×(48+52)运用了乘法分配律。
12.a+5=b+6应用了加法交换律。
13.125﹣45+55=125﹣(45+55)。
14.57×26=26×57,运用了乘法交换律。
15.1×2+3=1×3+2是运用了乘法的交换律。
四.计算题(共1小题)
16.用简便方法计算。
①8×9×125 ②205×17﹣5×17
五.应用题(共5小题)
17.果农李大伯把六筐香蕉送到水果超市,这六筐香蕉的质量依次是58kg、53kg、42kg、47kg、49kg、51kg。请你帮李大伯计算一下这六筐香蕉一共重多少千克。
18.小丽买如图的一套衣服和鞋子,一共要花多少钱?
19.某学校兴趣小组(不能重复参加)人员情况如下表:
小组名称 舞蹈 声乐 书法 乒乓球
人数 124 57 76 43
你能很快算出全校共有多少人参加兴趣小组吗?
20.一套运动服的上衣要97元,裤子要63元。现在需要购买这样的运动服35套,需要准备多少元钱?
21.卫生防疫站要为三个社区的适龄儿童注射疫苗,至少要准备多少个一次性注射器?
社区 融辉社区 幸福社区 红旗社区
适龄儿童人数 152 347 248
一.选择题(共5小题)
1.下列等式没有应用乘法交换律的是( )
A.甲×乙=乙×甲 B.a×b=b×a
C.9×8×5=9×(8×5)
2.若a+b=23,则(a+6)+(b﹣5)的结果是( )
A.22 B.23 C.24
3.55+64+145+36的简便算法是( )
A.(36+55)+(145+64) B.(36+145)+(64+55)
C.(36+64)+(145+55)
4.小明计算器上的数字键“9”坏了,下面( )算式可以算出199×4的得数。
A.200﹣1×4 B.200×4﹣4 C.200﹣4
5.下面运用加法结合律的式子是( )
A.45+76=46+75
B.63+72+128=63+(72+128)
C.128﹣75﹣45=128﹣(75﹣45)
D.a+b+c=b+a+c
二.填空题(共5小题)
6.(2+4+6+…+18+20)﹣(1+3+5+…17+19)= .
7.为使加法计算更加简便,学习了加法交换律和 律。根据这些运算定律,可以得知:650+258= +650,261+ +108=261+(92+108)
8.小燕在计算36×(□+20)时,错算成了36×□+20,那么错误的结果比正确的结果 (填“大”或“小”),错误的结果与正确的结果相差 。
9.(40+35)×50= × + × 应用了 律,用字母表示为 。
10.小刚的计算器上数字键“2”坏了,他要用计算器计算358×24,他可以怎样用这个计算器算出正确的结果?请写出2道不同的算式。 或 。
三.判断题(共5小题)
11.728+72﹣28=728﹣28+72。
12.a+b+c=b+(a+c)运用了加法交换律和加法结合律。
13.65+130+35+70=(65+35)+(130+70),只运用了加法交换律。
14.32×(7×3)=32×7+32×3. .
15.(a×b)×c=a×(c×b). .
四.计算题(共1小题)
16.简便运算。
208+106+192+194 8×(125+9)
56×99+56 25×37×4
五.应用题(共5小题)
17.
18.一只小猴喜欢吃香蕉,主人对它说:“每天早上吃三根,晚上吃四根。”小猴听了很生气。主人马上改口说:“那就早上吃四根,晚上吃三根吧!”小猴觉得自己占便宜了,很开心。对此,你是怎么想的?
19.小玲每天早上要喝一盒牛奶,吃一个蛋糕。
20.实验小学图书室有8个书架,每个书架都有7层,每层可放125本书.这些书架一共可放多少本书?
21.四季超市运来大米和面粉各48袋,大米每袋75千克,面粉每袋25千克,一共运来大米和面粉共多少千克?
一.选择题(共5小题)
1.与37×20的得数相等的算式是( )
A.20×37 B.27×20 C.2×37
2.(2021春 河东区期末)506+720+280=506+(720+280)运用了( )
A.加法交换律 B.加法结合律
C.乘法分配律 D.加法交换律和结合律
3.(2021春 钦州期末)下面算式中,( )所表示的不是加法交换律。
A.a+b=c+d B.20+a+b=a+b+20
C.a+x=x+a
4.(2022春 昆明月考)25×16与( )的结果相等。
A.25×10×6 B.25×4×4 C.25×10+6 D.20+5×16
5.(2022春 正安县期末)如果〇+ =10,那么78×〇+78× =( )
A.7800 B.780 C.78 D.无法确定
二.填空题(共5小题)
6.97+198+199+200+201+202+203+204= .
7.(2022秋 顺德区期中)如果用字母a、b、c表示算式(49×125)×8=49×(125×8)中的三个数,那么算式中的规律可以写成
8.(2022春 市中区期末)(100+2)×75=100×75+2×75,这里运用的运算律是 ,用字母表示这个运算律是 。
9.(2021秋 恩阳区 期末)360+ +108=360+(92+ )
10.(2021秋 华州区期中)运用加法交换律和乘法交换律填一填。
279+135= +279 72×138= ×
三.判断题(共5小题)
11.(2022秋 宁陕县期末)56×99=56×100﹣1
12.25×(7×4)=(25×4)×7
13.(2020秋 白云区期末)等式7bc=7(bc)是运用了乘法结合律。
14.(2022秋 上思县期末)整数的运算律对于分数同样适用。
15.(2022春 江汉区期末)54×70+54×28+2=54×(70+28+2)。
四.计算题(共1小题)
16.(2021秋 临洮县期末)脱式计算,能简算的要简算。
720+[(12+24)×2] 25×48+25×52 (125+16)×8
75+149+51+125 8×56×125 87×101
五.应用题(共5小题)
17.(2022秋 怀柔区期末)请你结合生活中的事例,用你喜欢的方式(可以画图,也可以讲数学故事……),说说等10+7+13=10+(7+13)为什么成立。
18.(2022春 德州期中)乒乓球训练馆买了1200个乒乓球,每25个装一袋,每4袋装一盒,需要准备多少个盒子?(用简便方法来计算)
19.(2022 南京模拟)小明从周一到周四每天踢毽子的次数如下:156下、195下、144下、205下。这四天他一共踢了多少下毽子?
20.(2021春 汤阴县期中)同学们从学校到博物馆要走1200米,先走了236米到新华书店,又走了464米到人民广场,同学们还要走多少米才能到博物馆?
中小学教育资源及组卷应用平台
21.(2022春 德州期中)学校食堂购进大米和面粉各204袋,大米每袋56元,面粉每袋44元。大米和面粉一共花了多少元?(用简便方法来计算)
苏教版数学四年级下册
第六单元 运算律
知识点01:加法交换律
两个数相加,交换两个加数的位置,和不变。
用字母表示:a+b=b+a。
知识点02:加法结合律
三个数相加,先把前两个数相加,再与第三个数相加,或者先把后两个数相加再与第一个数相加,和不变。
2. 用字母表示 :(a+b)+c=a+(b+c)。
知识点03:加法运算律的应用
在连加算式中,当某些加数相加可以凑成整十、整百整千......数时,应用加法运算律可以使计算简便。
知识点04:乘法交换律
两个数相乘交换两个录数的位置积不变
用字母表示:a×b=b×a。
知识点05:乘法结合律
1.三个数相乘,先把前两个数相乘,再与第三个数相乘,或者先把后两个数相乘,再与第一个数相乘积不变。
2. 用字母表示:(a×b)×c=a×(b×c)。
知识点06:乘法分配律
两个数的和与一个数相乘,可以先把这两个数分别与这个数相乘再相加。
用字母表示:(a+b)×c=a×c+b×c。
知识点07:乘法运算律的应用
在连乘算式中,当某两个乘数的积正好是整十、整百整千...数时,应用乘法运算律可以使计算简便.
两个数相乘,如果有一个数接近整百数可以先将这个数转化成整百数加或减一个数的形式,再应用乘法分配律进行计算。
在求两积之和的算式中,如果乘法算式中有一个乘数相同,另外两个乘数相加可以凑成整十、整百、整千...数时,可以根据乘法分配律的逆运算来计算。
知识点08:解决问题
解决问题之前,可以先画图或列表整理题中的条件和问题,再从不同的角度去思考,就会得到不同的解题方法。
考点01:加法运算律
【典例分析01】想一想,填一填.
【分析】根据整数加法的计算法则计算并填空即可.
【解答】解:
【点评】这道题目考查的是整数加法,属于基础题目,要熟练掌握并计算.
【变式训练01】想一想,填一填.
【分析】根据整数加法的运算法则计算即可.根据图示可知:31是蜻蜓的只数,23是蝴蝶的只数,求两数的和,就是求两种动物的总只数.
【解答】解:如图:
.
【点评】本题主要考查整数加法的应用,关键利用整数加法中交换两个加数的位置,和不变的规律计算.
【变式训练02】8746﹣3874+1874+1254.
【分析】通过观察,此题运用加法交换律与结合律简算.
【解答】解:8746﹣3874+1874+1254,
=(8746+1254)﹣(3874﹣1874),
=10000﹣2000,
=8000.
【点评】王成此题,应注意分时式中数据,运用合适的运算定律进行简算.
【变式训练03】我会填.(根据运算定律填空)
766+589=589+□
300+600=□+□
a+(b+18)=(□+□)+18
295+19+105=(□+□)+19
【分析】加法交换律:a+b=b+a.
加法结合律:(a+b)+c=a+(b+c).
第1、2 题利用加法交换律填空即可.
第3题利用加法结合律填空即可.
第4题利用加法交换律和加法结合律填空即可.
【解答】解:766+589=589+766
300+600=600+300
a+(b+18)=(a+b)+18
295+19+105=(295+105)+19.
故答案为:766;a,b;600,300;295,105.
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.
考点02:乘法运算律
【典例分析02】想一想,填一填.
【分析】一束百合5元,买20束需要20个5元,即20×5=100元;一束玫瑰20元,买5束需要5个20元,即5×20=100元;然后再进一步解答.
【解答】解:20×5=100(元)
表示20束百合的总钱数为100元;
5×20=100(元)
表示5束玫瑰的总钱数为100元;
所以,20×5=5×20.
故答案为:
.
【点评】考查了整数乘法的意义的灵活运用.
【变式训练01】你能很快说出每盏灯笼上三个数连加的和与三个数连乘的积吗?
【分析】三个数连加的和按照从左到右顺序解答;三个数连乘的积运用乘法交换律解答.
【解答】解:(1)4+16+5
=20+5
=25
4×16×5
=4×5×16
=20×16
=320
(2)25+35+4
=60+4
=64
25×35×4
=25×4×35
=100×35
=3500
填图如下:
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.
【变式训练02】用4块同样大小的长方形木板拼成一个广告牌(如图),已知每块木板长25dm,宽16dm,新广告牌的面积是多少平方米?(用两种方法解答)
【分析】(1)根据长方形的面积公式S=ab求出一个长方形的面积,然后再乘4即可;
(2)先求出新广告牌的长:25×4=100分米,宽16分米,再根据长方形的面积公式S=ab解答即可.
【解答】解:(1)25×16×4
=400×4
=1600(平方分米)
(2)25×4×16
=100×16
=1600(平方分米)
1600平方分米=16平方米
答:新广告牌的面积是16平方米.
【点评】本题考查了图形的拼组,关键是灵活运用长方形的面积公式S=ab.
【变式训练03】《百科知识》每套125元,《数学王国》每套35元。学校各买了6套,一共花多少钱?
【分析】用每套《百科知识》的价钱加每套《数学王国》的价钱,再乘6即可解答。
【解答】解:(125+35)×6
=160×6
=960(元)
答:一共花960元钱。
【点评】本题是经济问题应用题,根据单价×数量=总价进行解答。
考点03:运算定律与简便运算
【典例分析03】计算417﹣198时,可以这样想:417﹣198=417﹣200+2=219,请你试着用这样的方法计算:621+198= 621+200﹣2 = 819 。
【分析】计算417﹣198时,可以这样想:417﹣198=417﹣200+2=219,这是运用凑整法,把198,看成整百数200,减去200就多减了2,再加上2;计算621+198时可以把198看成200,621加200比621加198多加了2,再减去2即可。
【解答】解:621+198
=621+200﹣2
=819
故答案为:621+200﹣2,819。
【点评】本题考查了运用凑整法计算整数加法、减法的方法,注意找清楚多加了几或者多减去了几。
【变式训练01】25× 34 ×4=25× 4 ×34
a×8﹣b× 8 =〔a〇 b 〕× 8
【分析】根据乘法交换律填空即可;
按照乘法分配律进行填空。
【解答】解:25×34×4=25×4×34
a×8﹣b×8=〔a﹣b〕×8
故答案为:34,4,8,﹣,b,8。
【点评】本题主要考查了学生对运算定律的熟练掌握情况,牢记定律内容是解答本题的关键。
【变式训练02】两个加数相加,交换加数的位置,和不变,这叫做加法交换律,用字母表示是a+b=b+a,请你像第3题的同学一样,用一种喜欢的方式表示加法交换律的意思。
【分析】交换两个加数的位置,和不变,这叫做加法交换律,如两个小长方形拼成一个图形,无论怎么拼它们的面积和不变,由此解答。
【解答】解:加法交换律可以这样表示:
两个小长方形的面积分别是a和b,则两种拼法面积相等
即:a+b=b+a。(答案不唯一)
【点评】本题考查了学生对于加法交换律的理解。
【变式训练03】水果店运进28箱苹果和22箱梨,每箱苹果和梨都是25kg,这些苹果和梨一共多少千克?
【分析】先用28加上22求出各一箱的单价和,然后再乘每箱的质量即可。
【解答】解:(28+22)×25
=50×25
=1250(千克)
答:这些苹果和梨一共1250千克。
【点评】本题考查了学生对于乘法分配律的理解和实际运用。
一.选择题(共5小题)
1.(11+13+15+17+19)﹣(10+12+14+16+18)=( )
A.5 B.4 C.3 D.0
【分析】根据题意,减去10+12+14+16+18的和,就是分别减去它们各自的数,然后根据加法交换和结合律,带着符号进行结合,再进一步解答即可.
【解答】解:(11+13+15+17+19)﹣(10+12+14+16+18)
=11+13+15+17+19﹣10﹣12﹣14﹣16﹣18
=(11﹣10)+(13﹣12)+(15﹣14)+(17﹣16)+(19﹣18)
=1+1+1+1+1
=5
故选:A。
【点评】去掉括号注意符号的变化,带着符号进行交换与结合时,一定也要注意符号,然后进一步解答即可.
2.a+b+c+d=(a+d)+(b+c),这道算式运用了( )
A.加法交换律 B.加法结合律
C.加法交换律和结合律
【分析】根据加法交换律、加法结合律的意义:两个数相加,交换加数的位置,它们的和不变,这叫做加法交换律;
三个数相加,可以先把前两个数相加再加上第三个数,或者先把后两个数相加再加上第一个数,它们的和不变,这叫做加法结合律,由此解答即可。
【解答】解:根据分析可得:
a+b+c+d=(a+d)+(b+c),这道算式运用了:加法交换律和结合律。
故选:C。
【点评】此题考查的目的是理解加法交换律、结合律的意义,并能够灵活运用。
3.计算125×18×8时,明明是按照125×8×18来算的,他这样算的依据是( )
A.乘法结合律 B.乘法分配律 C.乘法交换律
【分析】根据乘法交换律a×b×c=a×c×b进行解答即可。
【解答】解:128×18×8=125×8×18
运用了乘法交换律。
故选:C。
【点评】熟练地掌握乘法交换律是解答本题的关键。
4.计算36×25时,这样计算:36×25=9×(4×25)=9×100=900,运用了( )
A.乘法交换律 B.乘法结合律 C.乘法分配律
【分析】根据乘法结合律a×b×c=a×(b×c)进行解答即可。
【解答】解:36×25
=9×4×25
=9×(4×25)
=9×100
=900
运用了乘法结合律。
故选:B。
【点评】熟练地掌握乘法结合律是解答本题的关键。
5.102×47=(100+2)×47=100×47+2×47运用了( )
A.乘法交换律 B.乘法分配律 C.乘法结合律 D.加法结合律
【分析】两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加,这叫做乘法分配律,用字母表示为:a×(b+c)=a×b+a×c;据此解答即可。
【解答】解:102×47
=(100+2)×47
=100×47+2×47
=4700+94
=4794
答:运用了乘法分配律。
故选:B。
【点评】熟练掌握乘法分配律是解答此题的关键。
二.填空题(共5小题)
6.a×b=b×a这个运算规律是 乘法交换 律.
【分析】乘法交换律:两个因数交换位置,积不变,据此判断即可.
【解答】解:a×b=b×a这个运算规律是乘法交换律.
故答案为:乘法交换.
【点评】此题主要考查了运算定律与简便运算,要熟练掌握,注意乘法交换律的应用.
7.根据加法结合律在横线上填上适当的数或字母。
a+(8+b)=( a + 8 )+b
【分析】a+8+b中,先计算后面两个数的和与先计算前面两个数的和,结果相同。
【解答】解:a+(8+b)=(a+8)+b
故答案为:a,8。
【点评】本题是一道有关加法的交换律和结合律的题目。
8.已知△﹣□=80,那么35×△﹣35×□= 2800 。
【分析】乘法分配律:两个数的和同一个数相乘,可以把两个加数分别和这个数相乘,再把两个积相加,结果不变。公式是:(a+b)×c=a×c+b×c。
【解答】解:已知△﹣□=80,
35×△﹣35×□
=35×(△﹣□)
=35×80
=2800
故答案为:2800。
【点评】此题主要考查了乘法分配律的应用,要熟练掌握。
9.根据学过的运算律填一填。
(1)38×2×5=38×( 2 ×5)
(2)(81+79)+21= 81 +( 79 +21)
【分析】根据乘法结合律a×b×c=a×(b×c)、加法结合律a+b+c=a+(b+c)进行解答即可。
【解答】解:(1)38×2×5=38×(2×5)
(2)(81+79)+21=81+(79+21)
故答案为:2;81,79。
【点评】熟练地掌握乘法、加法结合律是解答本题的关键。
10. 82 +45= 45 +82,这里运用了加法 交换律 ,用字母表示是 a+b=b+a 。
【分析】根据加法交换律a+b=b+a进行解答即可。
【解答】解:82+45=45+82,运用了加法交换律,字母表示是:a+b=b+a。
故答案为:82,45,交换律,a+b=b+a。
【点评】本题主要考查了学生对加法交换律公式的灵活掌握。
三.判断题(共5小题)
11.85×48+85×52=85×(48+52)运用了乘法分配律。 √
【分析】乘法分配律是指两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加,所以85×48+85×52=85×(48+52)运用了乘法分配律。
【解答】解:85×48+85×52=85×(48+52)运用了乘法分配律,
所以题中说法正确。
故答案为:√。
【点评】此题主要考查了乘法分配律的应用,要熟练掌握,解答此题的关键是要明确:乘法分配律是指两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。
12.a+5=b+6应用了加法交换律。 ×
【分析】根据加法交换律a+b=b+a进行判断。
【解答】解:a+5=b+6没有应用加法交换律,所以原题干说法错误。
故答案为:×。
【点评】本题主要考查了学生对加法交换律的掌握。
13.125﹣45+55=125﹣(45+55)。 ×
【分析】根据减法的运算性质a﹣b﹣c=a﹣(b+c),解答此题。
【解答】解:因为125﹣45﹣55=125﹣(45+55),所以125﹣45+55=125﹣(45+55)错误。
故答案为:×。
【点评】此题考查了减法运算性质的灵活运用。
14.57×26=26×57,运用了乘法交换律。 √
【分析】乘法交换律:两个因数相乘,交换因数的位置,积不变,两个因数的大小不变,只是位置交换了,据此判断即可。
【解答】解:因为运用乘法交换律时,两个因数的大小不变,只是位置交换了,
所以57×26=26×57运用了乘法交换律,
所以题中说法正确。
故答案为:√。
【点评】此题主要考查了运算定律与简便运算,要熟练掌握,注意运算顺序,注意加法交换律的应用。
15.1×2+3=1×3+2是运用了乘法的交换律。 ×
【分析】根据乘法交换律a×b=b×a进行解答即可。
【解答】解:1×2+3=6
1×3+2=5
两个算式的结果不相同,是不相等的算式,所以原题干说法错误。
故答案为:×。
【点评】本题主要考查了学生对乘法交换律的掌握,注意运算的准确性。
四.计算题(共1小题)
16.用简便方法计算。
①8×9×125 ②205×17﹣5×17
【分析】①根据乘法交换律简算;
②根据乘法分配律简算。
【解答】解:①8×9×125
=8×125×9
=1000×9
=9000
②205×17﹣5×17
=(205﹣5)×17
=200×17
=3400
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算。
五.应用题(共5小题)
17.果农李大伯把六筐香蕉送到水果超市,这六筐香蕉的质量依次是58kg、53kg、42kg、47kg、49kg、51kg。请你帮李大伯计算一下这六筐香蕉一共重多少千克。
【分析】根据题意,把这6筐香蕉的质量相加即可求解,注意计算时按照简便方法进行计算。
【解答】解:58+53+42+47+49+51
=(58+42)+(53+47)+(49+51)
=100+100+100
=300(千克)
答:这六筐香蕉一共重300千克。
【点评】此题主要依据加法的意义解决问题,解答时要注意简便方法的运用。
18.小丽买如图的一套衣服和鞋子,一共要花多少钱?
【分析】求一共要花多少钱,把一套衣服和鞋子的单价相加,再用加法结合律简算即可。
【解答】解:89+102+98
=89+(102+98)
=89+200
=289(元)
答:一共要花289元钱。
【点评】此题重点考查了学生对加法结合律的掌握与运用情况。
19.某学校兴趣小组(不能重复参加)人员情况如下表:
小组名称 舞蹈 声乐 书法 乒乓球
人数 124 57 76 43
你能很快算出全校共有多少人参加兴趣小组吗?
【分析】求全校共有多少人参加兴趣小组,把四个小组的人数相加,再用加法的交换律与结合律简算即可。
【解答】解:124+57+76+43
=(124+76)+(57+43)
=200+100
=300(人)
答:全校共有300人参加兴趣小组。
【点评】此题重点考查了学生对加法交换律和结合律的掌握与运用情况。
20.一套运动服的上衣要97元,裤子要63元。现在需要购买这样的运动服35套,需要准备多少元钱?
【分析】一套衣服需要(97+63)元,乘35即可求出总价。
【解答】解:(97+63)×35
=160×35
=5600(元)
答:需要准备5600元钱。
【点评】解答此题的关键是掌握求价格的相关公式。
21.卫生防疫站要为三个社区的适龄儿童注射疫苗,至少要准备多少个一次性注射器?
社区 融辉社区 幸福社区 红旗社区
适龄儿童人数 152 347 248
【分析】求至少要准备多少个一次性注射器,需要把三个社区适龄儿童人数相加,每个适龄儿童需要一个一次性注射器,据此解答即可.
【解答】解:152+347+248
=152+248+347
=400+347
=747(个)
答:至少要准备747个一次性注射器.
【点评】此题考查了整数加法的应用,要根据题意准确找出加数,此题要灵活运用加法交换律.
一.选择题(共5小题)
1.下列等式没有应用乘法交换律的是( )
A.甲×乙=乙×甲 B.a×b=b×a
C.9×8×5=9×(8×5)
【分析】根据乘法交换律a×b=b×a、乘法结合律a×b×c=a×(b×c)进行解答即可。
【解答】解:A甲×乙=乙×甲,运用了乘法交换律;
B.a×b=b×a,运用了乘法交换律;
C.9×8×5=9×(8×5),运用了乘法结合律。
没有应用乘法交换律的是9×8×5=9×(8×5)。
故选:C。
【点评】熟练地掌握乘法交换律、乘法结合律是解答本题的关键。
2.若a+b=23,则(a+6)+(b﹣5)的结果是( )
A.22 B.23 C.24
【分析】先把(a+6)+(b﹣5)化简为:a+b+6﹣5,再把a+b=23代入a+b+6﹣5计算即可。
【解答】解:(a+6)+(b﹣5)
=a+6+b﹣5
=a+b+6﹣5
=23+6﹣5
=29﹣5
=24
答:(a+6)+(b﹣5)的结果是24。
故选:C。
【点评】先把要求的式子化简,再运用代入法求值即可。
3.55+64+145+36的简便算法是( )
A.(36+55)+(145+64) B.(36+145)+(64+55)
C.(36+64)+(145+55)
【分析】运用加法交换律及结合律计算.
【解答】解:55+64+145+36
=36+64+145+55
=(36+64)+(145+55)
=100+200
=300
故选:C。
【点评】本题主要考查学生对加法交换律及结合律的掌握情况.
4.小明计算器上的数字键“9”坏了,下面( )算式可以算出199×4的得数。
A.200﹣1×4 B.200×4﹣4 C.200﹣4
【分析】199×4可以看作求199个4的和,它比200个4少1个4,1个4就是4,所以它等于200与4的积再减4。
【解答】解:199×4
=200×4﹣1×4
=200×4﹣4
故选:B。
【点评】此题重点考查乘法分配律的意义和应用。
5.下面运用加法结合律的式子是( )
A.45+76=46+75
B.63+72+128=63+(72+128)
C.128﹣75﹣45=128﹣(75﹣45)
D.a+b+c=b+a+c
【分析】根据加法结合律的意义,三个数相加,可以先前两个数相加,再加上第三个数,也可以先把后两个数相加,再加上第一个数,和不变。据此解答。
【解答】解:运用加法结合律的式子是:63+72+128=63+(72+128)。
故选:B。
【点评】此题考查的目的是理解掌握加法结合律的意义及应用。
二.填空题(共5小题)
6.(2+4+6+…+18+20)﹣(1+3+5+…17+19)= 10 .
【分析】根据题意可知,2+4+6+…+18+20是10个偶数相加的和,减去1+3+5+…17+19是10个奇数相加和,等于连续减去这10奇数,可得(2﹣1)+(4﹣3)+(6﹣5)+…+(18﹣17)+(20﹣19),可以得到10个1,然后再进一步解答即可.
【解答】解:(2+4+6+…+18+20)﹣(1+3+5+…17+19),
=2+4+6+…+18+20﹣1﹣3﹣5﹣…﹣17﹣19,
=(2﹣1)+(4﹣3)+(6﹣5)+…+(18﹣17)+(20﹣19),
=1+1+1+1+1+1+1+1+1+1,
=10.
【点评】本题的关键是根据连减的性质,把括号去掉,然后再根据加法交换律和结合律进一步解答即可.
7.为使加法计算更加简便,学习了加法交换律和 加法结合 律。根据这些运算定律,可以得知:650+258= 258 +650,261+ 92 +108=261+(92+108)
【分析】根据加法交换律a+b=b+a,加法结合律a+(b+c)=(a+b)+c,进行解答即可。
【解答】解:为使加法计算更加简便,学习了加法交换律和加法结合律。根据这些运算定律,可以得知:650+258=258+650,261+92+108=261+(92+108)。
故答案为:加法结合;258;92。
【点评】本题考查加法交换律和加法结合律的应用。注意计算的准确性。
8.小燕在计算36×(□+20)时,错算成了36×□+20,那么错误的结果比正确的结果 小 (填“大”或“小”),错误的结果与正确的结果相差 700 。
【分析】根据乘法分配律的意义,(a+b)×c=a×c+b×c,小燕在计算36×(□+20)时,错算成了36×□+20,显然错误结果比正确结果小,求出正确结果减去错误结果即可。
【解答】解:36×(□+20)
=36×□+36×20
=36×□+720
36×□+720﹣(36×□+20)
=36×□+720﹣36×□﹣20
=720﹣20
=700
答:错误的结果比正确的结果小,错误的结果与正确答案相差700。
故答案为:小,700。
【点评】此题先观察这两个算式的区别在什么地方,再对其中的一个变形,变成相接近的形式,进而求解。
9.(40+35)×50= 40 × 50 + 35 × 50 应用了 乘法分配 律,用字母表示为 (a+b)c=ac+bc 。
【分析】根据乘法分配律的意义,两个数的和与一个相乘,可以把两个加数分别与这个数相乘,然后把两个积相加,结果不变。据此解答。
【解答】解:(40+35)×50
=40×50+35×50
=2000+1750
=3750
应用了乘法分配律,用字母表示为:(a+b)c=ac+bc。
故答案为:40、50、35、50;乘法分配,(a+b)c=ac+bc。
【点评】此题考查的目的是理解掌握乘法分配律的意义及应用。
10.小刚的计算器上数字键“2”坏了,他要用计算器计算358×24,他可以怎样用这个计算器算出正确的结果?请写出2道不同的算式。 358×3×8 或 358×4×6 。
【分析】根据乘法的意义:358乘24,转化为358×3×8、358×4×6乘积,据此解答。
【解答】解:358×24,
转化为358×3×8、358×4×6乘积。
故答案为:358×3×8、358×4×6。
【点评】本题考查了数的拆分,关键吧24分成3与8、4与6的积,由此进行解答即可。
三.判断题(共5小题)
11.728+72﹣28=728﹣28+72。 √
【分析】加法交换律:两个加数交换位置,和不变。在同一级运算中,既可以按从左到右的运算顺序计算,也可交换﹣28与+72的位置,据此解答即可。
【解答】解:因为是同一级运算,可交换﹣28与+72的位置,所以728+72﹣28=728﹣28+72;所以原题说法正确。
故答案为:√。
【点评】此题重点考查了学生对加法交换律的掌握与运用情况。
12.a+b+c=b+(a+c)运用了加法交换律和加法结合律。 √
【分析】a+b+c=b+(a+c)是先交换了a和b的位置,然后把后两个加数结合在一起,由此求解。
【解答】解:a+b+c=b+(a+c)应用了加法交换律和加法结合律。原题说法正确。
故答案为:√。
【点评】①加法交换律:两个加数交换位置,和不变,如a+b=b+a;
②加法结合律:先把前两个数相加,或先把后两个数相加,和不变,如:a+b+c=a+(b+c)。
13.65+130+35+70=(65+35)+(130+70),只运用了加法交换律。 ×
【分析】根据加法交换律、加法结合律的意义,先运用加法交换律,再运用加法结合律简算。
【解答】解:65+130+35+70
=(65+35)+(130+70)
=100+200
=300
所以运用了加法交换律和加法结合律。
因此,题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解掌握加法交换律、加法结合律的意义,并且能够灵活运用加法交换律、加法结合律进行简算。
14.32×(7×3)=32×7+32×3. × .
【分析】本题应先算7×3,再与32相乘,不能用乘法分配律运算,因为不是32×(7+3)
【解答】解:32×(7×3)
=32×21
=672
不能运用乘法分配律来求解,因为不是32×(7+3)
所以题干的说法是错误的
故答案为:×
【点评】考查学生对乘法分配律的掌握情况.
15.(a×b)×c=a×(c×b). √ .
【分析】首先根据乘法结合律,可得(a×b)×c=a×(b×c);然后根据乘法交换律,可得a×(b×c)=a×(c×b),所以(a×b)×c=a×(c×b).
【解答】解:因为(a×b)×c=a×(c×b),
所以题中说法正确.
故答案为:√.
【点评】此题主要考查了运算定律与简便运算,要熟练掌握,注意乘法交换律和乘法结合律的应用.
四.计算题(共1小题)
16.简便运算。
208+106+192+194 8×(125+9)
56×99+56 25×37×4
【分析】(1)根据加法交换律和加法结合律简算;
(2)根据乘法分配律简算;
(3)根据乘法分配律简算;
(4)根据乘法交换律简算。
【解答】解:(1)208+106+192+194
=(208+192)+(106+194)
=400+300
=700
(2)8×(125+9)
=8×125+8×9
=1000+72
=1072
(3)56×99+56
=56×(99+1)
=56×100
=5600
(4)25×37×4
=25×4×37
=100×37
=3700
【点评】此题是考查四则混合运算,要仔细观察算式的特点,灵活运用一些定律进行简便计算。
五.应用题(共5小题)
17.
【分析】根据单价×数量=总价,可以运用乘法分配律,先求出买一件夹克衫和一条裤子需要多少元,再求出买4件夹克衫和4条裤子需要多少元,然后再加上一件短袖衫的价格即可。据此解答。
【解答】解:(65+45)×4+32
=110×4+32
=440+32
=472(元)
答:一共要付472元。
【点评】此题考查的目的是理解掌握单价、数量、总价三者之间的关系及应用,乘法分配律的意义及应用。
18.一只小猴喜欢吃香蕉,主人对它说:“每天早上吃三根,晚上吃四根。”小猴听了很生气。主人马上改口说:“那就早上吃四根,晚上吃三根吧!”小猴觉得自己占便宜了,很开心。对此,你是怎么想的?
【分析】猴子再精,也精不过主人。小猴每天早上吃的根数与晚上吃的根数之和,就是一天吃的根数,根据加法交换律,一天吃的根数不变。
【解答】解:3+4=4+3
小猴并没占到便宜,每天吃的根数不变。
【点评】此题是考查加法交换律的应用。交换两个加数的位置,和不变。
19.小玲每天早上要喝一盒牛奶,吃一个蛋糕。
【分析】根据题意,可以分别求出一个星期买牛奶花多少钱,买蛋糕花多少钱,然后合并起来,也可以根据乘法分配律,a×c+b×c=(a+b)×c,先求出一天买牛奶和蛋糕花多少钱,再求一个星期一共花多少钱。然后与30元进行比较即可,据此解答。
【解答】解:3×7+2×7
=21+14
=35(元)
或(3+2)×7
=5×7
=35(元)
30<35
答:不够。
【点评】此题考查的目的是理解整数乘法、加法的意义及应用,乘法分配律的意义及应用,整数大小比较的方法及应用。
20.实验小学图书室有8个书架,每个书架都有7层,每层可放125本书.这些书架一共可放多少本书?
【分析】先用每层放书的本数乘上7层,求出每个书架可以放几本书,再用每个书架放书的本数乘上8,即可求出8个书架可以放书的本数.
【解答】解:125×7×8
=125×8×7
=1000×7
=7000(本)
答:这些书架一共可放7000本书.
【点评】解决本题根据乘法的意义:求几个几是多少列出连乘算式求解即可.
21.四季超市运来大米和面粉各48袋,大米每袋75千克,面粉每袋25千克,一共运来大米和面粉共多少千克?
【分析】根据题意可知,大米的袋数×每袋大米的重量+面粉的袋数×每袋大米的重量=一共运来大米和面粉的总重量,依此列式并根据乘法分配律的特点进行计算即可。
【解答】解:48×75+48×25
=48×(75+25)
=48×100
=4800(千克)
答:一共运来大米和面粉共4800千克。
【点评】此题考查的是运用乘法分配律的特点解决实际问题,应熟练掌握。
一.选择题(共5小题)
1.与37×20的得数相等的算式是( )
A.20×37 B.27×20 C.2×37
【分析】乘法交换律:两个数相乘,交换因数的位置,积不变。用公式表示为:a×b=b×a。
【解答】解:37×20=20×37
故选:A。
【点评】本题利用具体的算式考查了学生对于乘法交换律的理解。
2.(2021春 河东区期末)506+720+280=506+(720+280)运用了( )
A.加法交换律 B.加法结合律
C.乘法分配律 D.加法交换律和结合律
【分析】根据加法结合律a+b+c=a+(b+c)进行解答即可。
【解答】解:506+720+280=506+(720+280)运用了加法结合律。
故选:B。
【点评】熟练地掌握加法结合律是解答本题的关键。
3.(2021春 钦州期末)下面算式中,( )所表示的不是加法交换律。
A.a+b=c+d B.20+a+b=a+b+20
C.a+x=x+a
【分析】根据加法交换律a+b=b+a进行解答即可。
【解答】解:A.a+b=c+d,表示的不是加法交换律;
B.20+a+b=a+b+20,表示的是加法交换律;
C.a+x=x+a,表示的是加法交换律。
故选:A。
【点评】熟练地掌握加法交换律是解答本题的关键。
4.(2022春 昆明月考)25×16与( )的结果相等。
A.25×10×6 B.25×4×4 C.25×10+6 D.20+5×16
【分析】因为25×4=100,所以把16分成4×4,则25×16=25×(4×4),再用乘法结合律,先算25×4=100,再算100×4即可解答。
【解答】解:25×16
=25×(4×4)
=25×4×4
=100×4
=400
答:25×16与25×4×4的结果相等。
故选:B。
【点评】本题考查了用乘法结合律灵活计算的能力。
5.(2022春 正安县期末)如果〇+ =10,那么78×〇+78× =( )
A.7800 B.780 C.78 D.无法确定
【分析】根据乘法分配律a×c+b×c=(a+b)×c进行解答即可。
【解答】解:78×〇+78×
=78×(〇+□)
=78×10
=780
故选:B。
【点评】熟练地掌握乘法分配律是解答本题的关键。
二.填空题(共5小题)
6.97+198+199+200+201+202+203+204= 1504 .
【分析】通过分析式中数据可以发现,只要把201、202、203、204分别写成200加一个一位数的形式,然后运用加法交换律和结合律,进行简算即可.
【解答】解:97+198+199+200+201+202+203+204,
=97+198+199+200+(200+1)+(200+2)+(200+3)+(200+4),
=97+198+199+200+200+1+200+2+200+3+200+4,
=(97+3)+(198+2)+(199+1)+200+200+200+200+200+4,
=100+200×7+4,
=1504.
故答案为:1504.
【点评】此题考查了加减法中的巧算,比较简单,只要认真观察,即可找到解题捷径.
7.(2022秋 顺德区期中)如果用字母a、b、c表示算式(49×125)×8=49×(125×8)中的三个数,那么算式中的规律可以写成 a×b×c=a×(b×c)
【分析】根据乘法结合律a×b×c=a×(b×c)进行解答即可。
【解答】解:(49×125)×8=49×(125×8),算式中的规律可以写成a×b×c=a×(b×c)。
故答案为:a×b×c=a×(b×c)。
【点评】本题主要考查了学生对乘法结合律的掌握。
8.(2022春 市中区期末)(100+2)×75=100×75+2×75,这里运用的运算律是 乘法分配律 ,用字母表示这个运算律是 (a+b)×c=a×c+b×c 。
【分析】根据乘法分配律(a+b)×c=a×c+b×c进行解答即可。
【解答】解:(100+2)×75=100×75+2×75,这里运用的运算律是乘法分配律,用字母表示这个运算律是(a+b)×c=a×c+b×c。
故答案为:乘法分配律,(a+b)×c=a×c+b×c。
【点评】熟练地掌握乘法分配律是解答本题的关键。
9.(2021秋 恩阳区 期末)360+ 92 +108=360+(92+ 108 )
【分析】根据加法结合律a+b+c=a+(b+c)进行解答即可。
【解答】解:360+92+108
=360+(92+108)
=360+200
=560
故答案为:92,108。
【点评】熟练地掌握加法结合律是解答本题的关键。
10.(2021秋 华州区期中)运用加法交换律和乘法交换律填一填。
279+135= 135 +279 72×138= 138 × 72
【分析】根据加法交换律、乘法交换律的意义,a+b=b+a,a×b=b×a,据此解答即可。
【解答】解:
279+135=135+279 72×138=138×72
故答案为:135,138,72。
【点评】此题考查的目的是理解掌握加法交换律、乘法交换律的意义及应用。
三.判断题(共5小题)
11.(2022秋 宁陕县期末)56×99=56×100﹣1 ×
【分析】根据题意,把99看作100﹣1,然后利用乘法的分配律解答.
【解答】解:56×99
=56×(100﹣1)
=56×100﹣1×56
=5600﹣56
=5544.
故答案为:×.
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.
12.25×(7×4)=(25×4)×7 √
【分析】根据乘法交换律a×b=b×a,乘法结合律a×b×c=a×(b×c)进行解答即可。
【解答】解:25×(7×4)
=(25×4)×7
=100×7
=700
所以原题干说法正确。
故答案为:√。
【点评】本题主要考查了学生对乘法交换律和结合律的掌握。
13.(2020秋 白云区期末)等式7bc=7(bc)是运用了乘法结合律。 √
【分析】乘法结合律:先乘前两个数,或先乘后两个数,积不变;用字母表示为:a×b×c=a×(b×c);据此解答。
【解答】解:由以上分析7bc=7(bc)运用了乘法结合律,所以原题干正确。
故答案为:√。
【点评】此题考查了学生对乘法结合律的掌握与运用。
14.(2022秋 上思县期末)整数的运算律对于分数同样适用。 √
【分析】整数加法、乘法的运算定律对于小数、分数同样适用。
【解答】解:整数加法的运算定律,对于分数同样适用,此说法正确。
故答案为:√。
【点评】此题考查的目的是使学生明确:整数加法、乘法的运算定律对于小数、分数同样适用。
15.(2022春 江汉区期末)54×70+54×28+2=54×(70+28+2)。 ×
【分析】根据乘法分配律的意义直接判断作答。
【解答】解:54×70+54×28+2
=54×(70+28)+2
=54×98+2
=54×100﹣54×2+2
=5400﹣108+2
=5294
原题说法错误。
故答案为:×。
【点评】解答本题的关键是熟记乘法分配律的公式:a×(b+c)=ab+ac。
四.计算题(共1小题)
16.(2021秋 临洮县期末)脱式计算,能简算的要简算。
720+[(12+24)×2] 25×48+25×52 (125+16)×8
75+149+51+125 8×56×125 87×101
【分析】(1)先算小括号里面的加法,再算中括号里面的乘法,最后算括号外的加法;
(2)根据乘法分配律简算;
(3)根据乘法分配律简算;
(4)根据加法交换律和加法结合律简算;
(5)根据乘法交换律简算;
(6)先把101分解成(100+1),再根据乘法分配律简算。
【解答】解:(1)720+[(12+24)×2]
=720+[36×2]
=720+72
=792
(2)25×48+25×52
=25×(48+52)
=25×100
=2500
(3)(125+16)×8
=125×8+16×8
=1000+128
=1128
(4)75+149+51+125
=(75+125)+(149+51)
=200+200
=400
(5)8×56×125
=8×125×56
=1000×56
=56000
(6)87×101
=87×(100+1)
=87×100+87×1
=8700+87
=8787
【点评】此题是考查四则混合运算,要仔细观察算式的特点,灵活运用一些定律进行简便计算。
五.应用题(共5小题)
17.(2022秋 怀柔区期末)请你结合生活中的事例,用你喜欢的方式(可以画图,也可以讲数学故事……),说说等10+7+13=10+(7+13)为什么成立。
【分析】10+7+13=10+(7+13)这是符合加法结合律的算式,可以举例说明加法结合律即可。
【解答】解:如图:三条线段的长度分别是10厘米,7厘米和13厘米,
那么三条线段的总长度可以表示为:
10+7+13=30(厘米)
也可以表示为:10+(7+13)=30(厘米)
所以:10+7+13=10+(7+13)。(答案不唯一)
【点评】本题考查了学生对于加法结合律的理解和应用。
18.(2022春 德州期中)乒乓球训练馆买了1200个乒乓球,每25个装一袋,每4袋装一盒,需要准备多少个盒子?(用简便方法来计算)
【分析】1200个乒乓球,每25个装一袋,用1200除以25求出1200里面有多少个25,就是可以装成多少袋,又每4袋装一盒,再用总袋数除以4,即可求出需要准备多少个盒子,计算时可以根据除法的性质计算。
【解答】解:1200÷25÷4
=1200÷(25×4)
=1200÷100
=12(个)
答:需要准备12个盒子。
【点评】解决本题根据除法的包含意义列出算式,再根据除法的计算性质进行简便运算。
19.(2022 南京模拟)小明从周一到周四每天踢毽子的次数如下:156下、195下、144下、205下。这四天他一共踢了多少下毽子?
【分析】求一共踢了多少下毽子,就是求和,把所有的加数相加156、195、144、205所得的和就是这四天他一共踢了多少下毽子。
【解答】解:156+195+144+205
=(156+144)+(195+205)
=300+400
=700(下)
答:这四天他一共踢了700下毽子。
【点评】本题考查了加法交换律和结合律的综合应用。
20.(2021春 汤阴县期中)同学们从学校到博物馆要走1200米,先走了236米到新华书店,又走了464米到人民广场,同学们还要走多少米才能到博物馆?
【分析】先用总路程减去236米,求出从新华书店道博物馆的路程,再减去464米,就是还要走的路程,计算时可以运用减法的性质进行简算。
【解答】解:1200﹣236﹣464
=1200﹣(236+464)
=1200﹣700
=500(米)
答:同学们还要走500米才能到博物馆。
【点评】解决本题也可以先求出已经走的路程,再用总路程减去已经走的路程即可;列式为1200﹣(236+464)。
21.(2022春 德州期中)学校食堂购进大米和面粉各204袋,大米每袋56元,面粉每袋44元。大米和面粉一共花了多少元?(用简便方法来计算)
【分析】大米每袋56元,204袋大米的价格就是204个56元,用56乘204即可求出大米的价格,同理求出面粉的价格,再相加即可,计算时根据乘法分配律简算。
【解答】解:56×204+44×204
=(56+44)×204
=100×204
=20400(元)
答:大米和面粉一共花了20400元。
【点评】解决本题根据乘法的意义列出算式,再根据乘法分配律简算。
第六单元 运算律
知识点01:加法交换律
两个数相加,交换两个加数的位置,和不变。
用字母表示:a+b=b+a。
知识点02:加法结合律
三个数相加,先把前两个数相加,再与第三个数相加,或者先把后两个数相加再与第一个数相加,和不变。
2. 用字母表示 :(a+b)+c=a+(b+c)。
知识点03:加法运算律的应用
在连加算式中,当某些加数相加可以凑成整十、整百整千......数时,应用加法运算律可以使计算简便。
知识点04:乘法交换律
两个数相乘交换两个录数的位置积不变
用字母表示:a×b=b×a。
知识点05:乘法结合律
1.三个数相乘,先把前两个数相乘,再与第三个数相乘,或者先把后两个数相乘,再与第一个数相乘积不变。
2. 用字母表示:(a×b)×c=a×(b×c)。
知识点06:乘法分配律
两个数的和与一个数相乘,可以先把这两个数分别与这个数相乘再相加。
用字母表示:(a+b)×c=a×c+b×c。
知识点07:乘法运算律的应用
在连乘算式中,当某两个乘数的积正好是整十、整百整千...数时,应用乘法运算律可以使计算简便.
两个数相乘,如果有一个数接近整百数可以先将这个数转化成整百数加或减一个数的形式,再应用乘法分配律进行计算。
在求两积之和的算式中,如果乘法算式中有一个乘数相同,另外两个乘数相加可以凑成整十、整百、整千...数时,可以根据乘法分配律的逆运算来计算。
知识点08:解决问题
解决问题之前,可以先画图或列表整理题中的条件和问题,再从不同的角度去思考,就会得到不同的解题方法。
考点01:加法运算律
【典例分析01】想一想,填一填.
【分析】根据整数加法的计算法则计算并填空即可.
【解答】解:
【点评】这道题目考查的是整数加法,属于基础题目,要熟练掌握并计算.
【变式训练01】想一想,填一填.
【变式训练02】8746﹣3874+1874+1254.
【变式训练03】我会填.(根据运算定律填空)
766+589=589+□
300+600=□+□
a+(b+18)=(□+□)+18
295+19+105=(□+□)+19
考点02:乘法运算律
【典例分析02】想一想,填一填.
【分析】一束百合5元,买20束需要20个5元,即20×5=100元;一束玫瑰20元,买5束需要5个20元,即5×20=100元;然后再进一步解答.
【解答】解:20×5=100(元)
表示20束百合的总钱数为100元;
5×20=100(元)
表示5束玫瑰的总钱数为100元;
所以,20×5=5×20.
故答案为:
.
【点评】考查了整数乘法的意义的灵活运用.
【变式训练01】你能很快说出每盏灯笼上三个数连加的和与三个数连乘的积吗?
【变式训练02】用4块同样大小的长方形木板拼成一个广告牌(如图),已知每块木板长25dm,宽16dm,新广告牌的面积是多少平方米?(用两种方法解答)
【变式训练03】《百科知识》每套125元,《数学王国》每套35元。学校各买了6套,一共花多少钱?
考点03:运算定律与简便运算
【典例分析03】计算417﹣198时,可以这样想:417﹣198=417﹣200+2=219,请你试着用这样的方法计算:621+198= 621+200﹣2 = 819 。
【分析】计算417﹣198时,可以这样想:417﹣198=417﹣200+2=219,这是运用凑整法,把198,看成整百数200,减去200就多减了2,再加上2;计算621+198时可以把198看成200,621加200比621加198多加了2,再减去2即可。
【解答】解:621+198
=621+200﹣2
=819
故答案为:621+200﹣2,819。
【点评】本题考查了运用凑整法计算整数加法、减法的方法,注意找清楚多加了几或者多减去了几。
【变式训练01】25× ×4=25× ×34
a×8﹣b× =〔a〇 〕×
【变式训练02】两个加数相加,交换加数的位置,和不变,这叫做加法交换律,用字母表示是a+b=b+a,请你像第3题的同学一样,用一种喜欢的方式表示加法交换律的意思。
【变式训练03】水果店运进28箱苹果和22箱梨,每箱苹果和梨都是25kg,这些苹果和梨一共多少千克?
一.选择题(共5小题)
1.(11+13+15+17+19)﹣(10+12+14+16+18)=( )
A.5 B.4 C.3 D.0
2.a+b+c+d=(a+d)+(b+c),这道算式运用了( )
A.加法交换律 B.加法结合律
C.加法交换律和结合律
3.计算125×18×8时,明明是按照125×8×18来算的,他这样算的依据是( )
A.乘法结合律 B.乘法分配律 C.乘法交换律
4.计算36×25时,这样计算:36×25=9×(4×25)=9×100=900,运用了( )
A.乘法交换律 B.乘法结合律 C.乘法分配律
5.102×47=(100+2)×47=100×47+2×47运用了( )
A.乘法交换律 B.乘法分配律 C.乘法结合律 D.加法结合律
二.填空题(共5小题)
6.a×b=b×a这个运算规律是 律.
7.根据加法结合律在横线上填上适当的数或字母。
a+(8+b)=( + )+b
8.已知△﹣□=80,那么35×△﹣35×□= 。
9.根据学过的运算律填一填。
(1)38×2×5=38×( ×5)
(2)(81+79)+21= +( +21)
10. +45= +82,这里运用了加法 ,用字母表示是 。
三.判断题(共5小题)
11.85×48+85×52=85×(48+52)运用了乘法分配律。
12.a+5=b+6应用了加法交换律。
13.125﹣45+55=125﹣(45+55)。
14.57×26=26×57,运用了乘法交换律。
15.1×2+3=1×3+2是运用了乘法的交换律。
四.计算题(共1小题)
16.用简便方法计算。
①8×9×125 ②205×17﹣5×17
五.应用题(共5小题)
17.果农李大伯把六筐香蕉送到水果超市,这六筐香蕉的质量依次是58kg、53kg、42kg、47kg、49kg、51kg。请你帮李大伯计算一下这六筐香蕉一共重多少千克。
18.小丽买如图的一套衣服和鞋子,一共要花多少钱?
19.某学校兴趣小组(不能重复参加)人员情况如下表:
小组名称 舞蹈 声乐 书法 乒乓球
人数 124 57 76 43
你能很快算出全校共有多少人参加兴趣小组吗?
20.一套运动服的上衣要97元,裤子要63元。现在需要购买这样的运动服35套,需要准备多少元钱?
21.卫生防疫站要为三个社区的适龄儿童注射疫苗,至少要准备多少个一次性注射器?
社区 融辉社区 幸福社区 红旗社区
适龄儿童人数 152 347 248
一.选择题(共5小题)
1.下列等式没有应用乘法交换律的是( )
A.甲×乙=乙×甲 B.a×b=b×a
C.9×8×5=9×(8×5)
2.若a+b=23,则(a+6)+(b﹣5)的结果是( )
A.22 B.23 C.24
3.55+64+145+36的简便算法是( )
A.(36+55)+(145+64) B.(36+145)+(64+55)
C.(36+64)+(145+55)
4.小明计算器上的数字键“9”坏了,下面( )算式可以算出199×4的得数。
A.200﹣1×4 B.200×4﹣4 C.200﹣4
5.下面运用加法结合律的式子是( )
A.45+76=46+75
B.63+72+128=63+(72+128)
C.128﹣75﹣45=128﹣(75﹣45)
D.a+b+c=b+a+c
二.填空题(共5小题)
6.(2+4+6+…+18+20)﹣(1+3+5+…17+19)= .
7.为使加法计算更加简便,学习了加法交换律和 律。根据这些运算定律,可以得知:650+258= +650,261+ +108=261+(92+108)
8.小燕在计算36×(□+20)时,错算成了36×□+20,那么错误的结果比正确的结果 (填“大”或“小”),错误的结果与正确的结果相差 。
9.(40+35)×50= × + × 应用了 律,用字母表示为 。
10.小刚的计算器上数字键“2”坏了,他要用计算器计算358×24,他可以怎样用这个计算器算出正确的结果?请写出2道不同的算式。 或 。
三.判断题(共5小题)
11.728+72﹣28=728﹣28+72。
12.a+b+c=b+(a+c)运用了加法交换律和加法结合律。
13.65+130+35+70=(65+35)+(130+70),只运用了加法交换律。
14.32×(7×3)=32×7+32×3. .
15.(a×b)×c=a×(c×b). .
四.计算题(共1小题)
16.简便运算。
208+106+192+194 8×(125+9)
56×99+56 25×37×4
五.应用题(共5小题)
17.
18.一只小猴喜欢吃香蕉,主人对它说:“每天早上吃三根,晚上吃四根。”小猴听了很生气。主人马上改口说:“那就早上吃四根,晚上吃三根吧!”小猴觉得自己占便宜了,很开心。对此,你是怎么想的?
19.小玲每天早上要喝一盒牛奶,吃一个蛋糕。
20.实验小学图书室有8个书架,每个书架都有7层,每层可放125本书.这些书架一共可放多少本书?
21.四季超市运来大米和面粉各48袋,大米每袋75千克,面粉每袋25千克,一共运来大米和面粉共多少千克?
一.选择题(共5小题)
1.与37×20的得数相等的算式是( )
A.20×37 B.27×20 C.2×37
2.(2021春 河东区期末)506+720+280=506+(720+280)运用了( )
A.加法交换律 B.加法结合律
C.乘法分配律 D.加法交换律和结合律
3.(2021春 钦州期末)下面算式中,( )所表示的不是加法交换律。
A.a+b=c+d B.20+a+b=a+b+20
C.a+x=x+a
4.(2022春 昆明月考)25×16与( )的结果相等。
A.25×10×6 B.25×4×4 C.25×10+6 D.20+5×16
5.(2022春 正安县期末)如果〇+ =10,那么78×〇+78× =( )
A.7800 B.780 C.78 D.无法确定
二.填空题(共5小题)
6.97+198+199+200+201+202+203+204= .
7.(2022秋 顺德区期中)如果用字母a、b、c表示算式(49×125)×8=49×(125×8)中的三个数,那么算式中的规律可以写成
8.(2022春 市中区期末)(100+2)×75=100×75+2×75,这里运用的运算律是 ,用字母表示这个运算律是 。
9.(2021秋 恩阳区 期末)360+ +108=360+(92+ )
10.(2021秋 华州区期中)运用加法交换律和乘法交换律填一填。
279+135= +279 72×138= ×
三.判断题(共5小题)
11.(2022秋 宁陕县期末)56×99=56×100﹣1
12.25×(7×4)=(25×4)×7
13.(2020秋 白云区期末)等式7bc=7(bc)是运用了乘法结合律。
14.(2022秋 上思县期末)整数的运算律对于分数同样适用。
15.(2022春 江汉区期末)54×70+54×28+2=54×(70+28+2)。
四.计算题(共1小题)
16.(2021秋 临洮县期末)脱式计算,能简算的要简算。
720+[(12+24)×2] 25×48+25×52 (125+16)×8
75+149+51+125 8×56×125 87×101
五.应用题(共5小题)
17.(2022秋 怀柔区期末)请你结合生活中的事例,用你喜欢的方式(可以画图,也可以讲数学故事……),说说等10+7+13=10+(7+13)为什么成立。
18.(2022春 德州期中)乒乓球训练馆买了1200个乒乓球,每25个装一袋,每4袋装一盒,需要准备多少个盒子?(用简便方法来计算)
19.(2022 南京模拟)小明从周一到周四每天踢毽子的次数如下:156下、195下、144下、205下。这四天他一共踢了多少下毽子?
20.(2021春 汤阴县期中)同学们从学校到博物馆要走1200米,先走了236米到新华书店,又走了464米到人民广场,同学们还要走多少米才能到博物馆?
中小学教育资源及组卷应用平台
21.(2022春 德州期中)学校食堂购进大米和面粉各204袋,大米每袋56元,面粉每袋44元。大米和面粉一共花了多少元?(用简便方法来计算)
苏教版数学四年级下册
第六单元 运算律
知识点01:加法交换律
两个数相加,交换两个加数的位置,和不变。
用字母表示:a+b=b+a。
知识点02:加法结合律
三个数相加,先把前两个数相加,再与第三个数相加,或者先把后两个数相加再与第一个数相加,和不变。
2. 用字母表示 :(a+b)+c=a+(b+c)。
知识点03:加法运算律的应用
在连加算式中,当某些加数相加可以凑成整十、整百整千......数时,应用加法运算律可以使计算简便。
知识点04:乘法交换律
两个数相乘交换两个录数的位置积不变
用字母表示:a×b=b×a。
知识点05:乘法结合律
1.三个数相乘,先把前两个数相乘,再与第三个数相乘,或者先把后两个数相乘,再与第一个数相乘积不变。
2. 用字母表示:(a×b)×c=a×(b×c)。
知识点06:乘法分配律
两个数的和与一个数相乘,可以先把这两个数分别与这个数相乘再相加。
用字母表示:(a+b)×c=a×c+b×c。
知识点07:乘法运算律的应用
在连乘算式中,当某两个乘数的积正好是整十、整百整千...数时,应用乘法运算律可以使计算简便.
两个数相乘,如果有一个数接近整百数可以先将这个数转化成整百数加或减一个数的形式,再应用乘法分配律进行计算。
在求两积之和的算式中,如果乘法算式中有一个乘数相同,另外两个乘数相加可以凑成整十、整百、整千...数时,可以根据乘法分配律的逆运算来计算。
知识点08:解决问题
解决问题之前,可以先画图或列表整理题中的条件和问题,再从不同的角度去思考,就会得到不同的解题方法。
考点01:加法运算律
【典例分析01】想一想,填一填.
【分析】根据整数加法的计算法则计算并填空即可.
【解答】解:
【点评】这道题目考查的是整数加法,属于基础题目,要熟练掌握并计算.
【变式训练01】想一想,填一填.
【分析】根据整数加法的运算法则计算即可.根据图示可知:31是蜻蜓的只数,23是蝴蝶的只数,求两数的和,就是求两种动物的总只数.
【解答】解:如图:
.
【点评】本题主要考查整数加法的应用,关键利用整数加法中交换两个加数的位置,和不变的规律计算.
【变式训练02】8746﹣3874+1874+1254.
【分析】通过观察,此题运用加法交换律与结合律简算.
【解答】解:8746﹣3874+1874+1254,
=(8746+1254)﹣(3874﹣1874),
=10000﹣2000,
=8000.
【点评】王成此题,应注意分时式中数据,运用合适的运算定律进行简算.
【变式训练03】我会填.(根据运算定律填空)
766+589=589+□
300+600=□+□
a+(b+18)=(□+□)+18
295+19+105=(□+□)+19
【分析】加法交换律:a+b=b+a.
加法结合律:(a+b)+c=a+(b+c).
第1、2 题利用加法交换律填空即可.
第3题利用加法结合律填空即可.
第4题利用加法交换律和加法结合律填空即可.
【解答】解:766+589=589+766
300+600=600+300
a+(b+18)=(a+b)+18
295+19+105=(295+105)+19.
故答案为:766;a,b;600,300;295,105.
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.
考点02:乘法运算律
【典例分析02】想一想,填一填.
【分析】一束百合5元,买20束需要20个5元,即20×5=100元;一束玫瑰20元,买5束需要5个20元,即5×20=100元;然后再进一步解答.
【解答】解:20×5=100(元)
表示20束百合的总钱数为100元;
5×20=100(元)
表示5束玫瑰的总钱数为100元;
所以,20×5=5×20.
故答案为:
.
【点评】考查了整数乘法的意义的灵活运用.
【变式训练01】你能很快说出每盏灯笼上三个数连加的和与三个数连乘的积吗?
【分析】三个数连加的和按照从左到右顺序解答;三个数连乘的积运用乘法交换律解答.
【解答】解:(1)4+16+5
=20+5
=25
4×16×5
=4×5×16
=20×16
=320
(2)25+35+4
=60+4
=64
25×35×4
=25×4×35
=100×35
=3500
填图如下:
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.
【变式训练02】用4块同样大小的长方形木板拼成一个广告牌(如图),已知每块木板长25dm,宽16dm,新广告牌的面积是多少平方米?(用两种方法解答)
【分析】(1)根据长方形的面积公式S=ab求出一个长方形的面积,然后再乘4即可;
(2)先求出新广告牌的长:25×4=100分米,宽16分米,再根据长方形的面积公式S=ab解答即可.
【解答】解:(1)25×16×4
=400×4
=1600(平方分米)
(2)25×4×16
=100×16
=1600(平方分米)
1600平方分米=16平方米
答:新广告牌的面积是16平方米.
【点评】本题考查了图形的拼组,关键是灵活运用长方形的面积公式S=ab.
【变式训练03】《百科知识》每套125元,《数学王国》每套35元。学校各买了6套,一共花多少钱?
【分析】用每套《百科知识》的价钱加每套《数学王国》的价钱,再乘6即可解答。
【解答】解:(125+35)×6
=160×6
=960(元)
答:一共花960元钱。
【点评】本题是经济问题应用题,根据单价×数量=总价进行解答。
考点03:运算定律与简便运算
【典例分析03】计算417﹣198时,可以这样想:417﹣198=417﹣200+2=219,请你试着用这样的方法计算:621+198= 621+200﹣2 = 819 。
【分析】计算417﹣198时,可以这样想:417﹣198=417﹣200+2=219,这是运用凑整法,把198,看成整百数200,减去200就多减了2,再加上2;计算621+198时可以把198看成200,621加200比621加198多加了2,再减去2即可。
【解答】解:621+198
=621+200﹣2
=819
故答案为:621+200﹣2,819。
【点评】本题考查了运用凑整法计算整数加法、减法的方法,注意找清楚多加了几或者多减去了几。
【变式训练01】25× 34 ×4=25× 4 ×34
a×8﹣b× 8 =〔a〇 b 〕× 8
【分析】根据乘法交换律填空即可;
按照乘法分配律进行填空。
【解答】解:25×34×4=25×4×34
a×8﹣b×8=〔a﹣b〕×8
故答案为:34,4,8,﹣,b,8。
【点评】本题主要考查了学生对运算定律的熟练掌握情况,牢记定律内容是解答本题的关键。
【变式训练02】两个加数相加,交换加数的位置,和不变,这叫做加法交换律,用字母表示是a+b=b+a,请你像第3题的同学一样,用一种喜欢的方式表示加法交换律的意思。
【分析】交换两个加数的位置,和不变,这叫做加法交换律,如两个小长方形拼成一个图形,无论怎么拼它们的面积和不变,由此解答。
【解答】解:加法交换律可以这样表示:
两个小长方形的面积分别是a和b,则两种拼法面积相等
即:a+b=b+a。(答案不唯一)
【点评】本题考查了学生对于加法交换律的理解。
【变式训练03】水果店运进28箱苹果和22箱梨,每箱苹果和梨都是25kg,这些苹果和梨一共多少千克?
【分析】先用28加上22求出各一箱的单价和,然后再乘每箱的质量即可。
【解答】解:(28+22)×25
=50×25
=1250(千克)
答:这些苹果和梨一共1250千克。
【点评】本题考查了学生对于乘法分配律的理解和实际运用。
一.选择题(共5小题)
1.(11+13+15+17+19)﹣(10+12+14+16+18)=( )
A.5 B.4 C.3 D.0
【分析】根据题意,减去10+12+14+16+18的和,就是分别减去它们各自的数,然后根据加法交换和结合律,带着符号进行结合,再进一步解答即可.
【解答】解:(11+13+15+17+19)﹣(10+12+14+16+18)
=11+13+15+17+19﹣10﹣12﹣14﹣16﹣18
=(11﹣10)+(13﹣12)+(15﹣14)+(17﹣16)+(19﹣18)
=1+1+1+1+1
=5
故选:A。
【点评】去掉括号注意符号的变化,带着符号进行交换与结合时,一定也要注意符号,然后进一步解答即可.
2.a+b+c+d=(a+d)+(b+c),这道算式运用了( )
A.加法交换律 B.加法结合律
C.加法交换律和结合律
【分析】根据加法交换律、加法结合律的意义:两个数相加,交换加数的位置,它们的和不变,这叫做加法交换律;
三个数相加,可以先把前两个数相加再加上第三个数,或者先把后两个数相加再加上第一个数,它们的和不变,这叫做加法结合律,由此解答即可。
【解答】解:根据分析可得:
a+b+c+d=(a+d)+(b+c),这道算式运用了:加法交换律和结合律。
故选:C。
【点评】此题考查的目的是理解加法交换律、结合律的意义,并能够灵活运用。
3.计算125×18×8时,明明是按照125×8×18来算的,他这样算的依据是( )
A.乘法结合律 B.乘法分配律 C.乘法交换律
【分析】根据乘法交换律a×b×c=a×c×b进行解答即可。
【解答】解:128×18×8=125×8×18
运用了乘法交换律。
故选:C。
【点评】熟练地掌握乘法交换律是解答本题的关键。
4.计算36×25时,这样计算:36×25=9×(4×25)=9×100=900,运用了( )
A.乘法交换律 B.乘法结合律 C.乘法分配律
【分析】根据乘法结合律a×b×c=a×(b×c)进行解答即可。
【解答】解:36×25
=9×4×25
=9×(4×25)
=9×100
=900
运用了乘法结合律。
故选:B。
【点评】熟练地掌握乘法结合律是解答本题的关键。
5.102×47=(100+2)×47=100×47+2×47运用了( )
A.乘法交换律 B.乘法分配律 C.乘法结合律 D.加法结合律
【分析】两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加,这叫做乘法分配律,用字母表示为:a×(b+c)=a×b+a×c;据此解答即可。
【解答】解:102×47
=(100+2)×47
=100×47+2×47
=4700+94
=4794
答:运用了乘法分配律。
故选:B。
【点评】熟练掌握乘法分配律是解答此题的关键。
二.填空题(共5小题)
6.a×b=b×a这个运算规律是 乘法交换 律.
【分析】乘法交换律:两个因数交换位置,积不变,据此判断即可.
【解答】解:a×b=b×a这个运算规律是乘法交换律.
故答案为:乘法交换.
【点评】此题主要考查了运算定律与简便运算,要熟练掌握,注意乘法交换律的应用.
7.根据加法结合律在横线上填上适当的数或字母。
a+(8+b)=( a + 8 )+b
【分析】a+8+b中,先计算后面两个数的和与先计算前面两个数的和,结果相同。
【解答】解:a+(8+b)=(a+8)+b
故答案为:a,8。
【点评】本题是一道有关加法的交换律和结合律的题目。
8.已知△﹣□=80,那么35×△﹣35×□= 2800 。
【分析】乘法分配律:两个数的和同一个数相乘,可以把两个加数分别和这个数相乘,再把两个积相加,结果不变。公式是:(a+b)×c=a×c+b×c。
【解答】解:已知△﹣□=80,
35×△﹣35×□
=35×(△﹣□)
=35×80
=2800
故答案为:2800。
【点评】此题主要考查了乘法分配律的应用,要熟练掌握。
9.根据学过的运算律填一填。
(1)38×2×5=38×( 2 ×5)
(2)(81+79)+21= 81 +( 79 +21)
【分析】根据乘法结合律a×b×c=a×(b×c)、加法结合律a+b+c=a+(b+c)进行解答即可。
【解答】解:(1)38×2×5=38×(2×5)
(2)(81+79)+21=81+(79+21)
故答案为:2;81,79。
【点评】熟练地掌握乘法、加法结合律是解答本题的关键。
10. 82 +45= 45 +82,这里运用了加法 交换律 ,用字母表示是 a+b=b+a 。
【分析】根据加法交换律a+b=b+a进行解答即可。
【解答】解:82+45=45+82,运用了加法交换律,字母表示是:a+b=b+a。
故答案为:82,45,交换律,a+b=b+a。
【点评】本题主要考查了学生对加法交换律公式的灵活掌握。
三.判断题(共5小题)
11.85×48+85×52=85×(48+52)运用了乘法分配律。 √
【分析】乘法分配律是指两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加,所以85×48+85×52=85×(48+52)运用了乘法分配律。
【解答】解:85×48+85×52=85×(48+52)运用了乘法分配律,
所以题中说法正确。
故答案为:√。
【点评】此题主要考查了乘法分配律的应用,要熟练掌握,解答此题的关键是要明确:乘法分配律是指两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。
12.a+5=b+6应用了加法交换律。 ×
【分析】根据加法交换律a+b=b+a进行判断。
【解答】解:a+5=b+6没有应用加法交换律,所以原题干说法错误。
故答案为:×。
【点评】本题主要考查了学生对加法交换律的掌握。
13.125﹣45+55=125﹣(45+55)。 ×
【分析】根据减法的运算性质a﹣b﹣c=a﹣(b+c),解答此题。
【解答】解:因为125﹣45﹣55=125﹣(45+55),所以125﹣45+55=125﹣(45+55)错误。
故答案为:×。
【点评】此题考查了减法运算性质的灵活运用。
14.57×26=26×57,运用了乘法交换律。 √
【分析】乘法交换律:两个因数相乘,交换因数的位置,积不变,两个因数的大小不变,只是位置交换了,据此判断即可。
【解答】解:因为运用乘法交换律时,两个因数的大小不变,只是位置交换了,
所以57×26=26×57运用了乘法交换律,
所以题中说法正确。
故答案为:√。
【点评】此题主要考查了运算定律与简便运算,要熟练掌握,注意运算顺序,注意加法交换律的应用。
15.1×2+3=1×3+2是运用了乘法的交换律。 ×
【分析】根据乘法交换律a×b=b×a进行解答即可。
【解答】解:1×2+3=6
1×3+2=5
两个算式的结果不相同,是不相等的算式,所以原题干说法错误。
故答案为:×。
【点评】本题主要考查了学生对乘法交换律的掌握,注意运算的准确性。
四.计算题(共1小题)
16.用简便方法计算。
①8×9×125 ②205×17﹣5×17
【分析】①根据乘法交换律简算;
②根据乘法分配律简算。
【解答】解:①8×9×125
=8×125×9
=1000×9
=9000
②205×17﹣5×17
=(205﹣5)×17
=200×17
=3400
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算。
五.应用题(共5小题)
17.果农李大伯把六筐香蕉送到水果超市,这六筐香蕉的质量依次是58kg、53kg、42kg、47kg、49kg、51kg。请你帮李大伯计算一下这六筐香蕉一共重多少千克。
【分析】根据题意,把这6筐香蕉的质量相加即可求解,注意计算时按照简便方法进行计算。
【解答】解:58+53+42+47+49+51
=(58+42)+(53+47)+(49+51)
=100+100+100
=300(千克)
答:这六筐香蕉一共重300千克。
【点评】此题主要依据加法的意义解决问题,解答时要注意简便方法的运用。
18.小丽买如图的一套衣服和鞋子,一共要花多少钱?
【分析】求一共要花多少钱,把一套衣服和鞋子的单价相加,再用加法结合律简算即可。
【解答】解:89+102+98
=89+(102+98)
=89+200
=289(元)
答:一共要花289元钱。
【点评】此题重点考查了学生对加法结合律的掌握与运用情况。
19.某学校兴趣小组(不能重复参加)人员情况如下表:
小组名称 舞蹈 声乐 书法 乒乓球
人数 124 57 76 43
你能很快算出全校共有多少人参加兴趣小组吗?
【分析】求全校共有多少人参加兴趣小组,把四个小组的人数相加,再用加法的交换律与结合律简算即可。
【解答】解:124+57+76+43
=(124+76)+(57+43)
=200+100
=300(人)
答:全校共有300人参加兴趣小组。
【点评】此题重点考查了学生对加法交换律和结合律的掌握与运用情况。
20.一套运动服的上衣要97元,裤子要63元。现在需要购买这样的运动服35套,需要准备多少元钱?
【分析】一套衣服需要(97+63)元,乘35即可求出总价。
【解答】解:(97+63)×35
=160×35
=5600(元)
答:需要准备5600元钱。
【点评】解答此题的关键是掌握求价格的相关公式。
21.卫生防疫站要为三个社区的适龄儿童注射疫苗,至少要准备多少个一次性注射器?
社区 融辉社区 幸福社区 红旗社区
适龄儿童人数 152 347 248
【分析】求至少要准备多少个一次性注射器,需要把三个社区适龄儿童人数相加,每个适龄儿童需要一个一次性注射器,据此解答即可.
【解答】解:152+347+248
=152+248+347
=400+347
=747(个)
答:至少要准备747个一次性注射器.
【点评】此题考查了整数加法的应用,要根据题意准确找出加数,此题要灵活运用加法交换律.
一.选择题(共5小题)
1.下列等式没有应用乘法交换律的是( )
A.甲×乙=乙×甲 B.a×b=b×a
C.9×8×5=9×(8×5)
【分析】根据乘法交换律a×b=b×a、乘法结合律a×b×c=a×(b×c)进行解答即可。
【解答】解:A甲×乙=乙×甲,运用了乘法交换律;
B.a×b=b×a,运用了乘法交换律;
C.9×8×5=9×(8×5),运用了乘法结合律。
没有应用乘法交换律的是9×8×5=9×(8×5)。
故选:C。
【点评】熟练地掌握乘法交换律、乘法结合律是解答本题的关键。
2.若a+b=23,则(a+6)+(b﹣5)的结果是( )
A.22 B.23 C.24
【分析】先把(a+6)+(b﹣5)化简为:a+b+6﹣5,再把a+b=23代入a+b+6﹣5计算即可。
【解答】解:(a+6)+(b﹣5)
=a+6+b﹣5
=a+b+6﹣5
=23+6﹣5
=29﹣5
=24
答:(a+6)+(b﹣5)的结果是24。
故选:C。
【点评】先把要求的式子化简,再运用代入法求值即可。
3.55+64+145+36的简便算法是( )
A.(36+55)+(145+64) B.(36+145)+(64+55)
C.(36+64)+(145+55)
【分析】运用加法交换律及结合律计算.
【解答】解:55+64+145+36
=36+64+145+55
=(36+64)+(145+55)
=100+200
=300
故选:C。
【点评】本题主要考查学生对加法交换律及结合律的掌握情况.
4.小明计算器上的数字键“9”坏了,下面( )算式可以算出199×4的得数。
A.200﹣1×4 B.200×4﹣4 C.200﹣4
【分析】199×4可以看作求199个4的和,它比200个4少1个4,1个4就是4,所以它等于200与4的积再减4。
【解答】解:199×4
=200×4﹣1×4
=200×4﹣4
故选:B。
【点评】此题重点考查乘法分配律的意义和应用。
5.下面运用加法结合律的式子是( )
A.45+76=46+75
B.63+72+128=63+(72+128)
C.128﹣75﹣45=128﹣(75﹣45)
D.a+b+c=b+a+c
【分析】根据加法结合律的意义,三个数相加,可以先前两个数相加,再加上第三个数,也可以先把后两个数相加,再加上第一个数,和不变。据此解答。
【解答】解:运用加法结合律的式子是:63+72+128=63+(72+128)。
故选:B。
【点评】此题考查的目的是理解掌握加法结合律的意义及应用。
二.填空题(共5小题)
6.(2+4+6+…+18+20)﹣(1+3+5+…17+19)= 10 .
【分析】根据题意可知,2+4+6+…+18+20是10个偶数相加的和,减去1+3+5+…17+19是10个奇数相加和,等于连续减去这10奇数,可得(2﹣1)+(4﹣3)+(6﹣5)+…+(18﹣17)+(20﹣19),可以得到10个1,然后再进一步解答即可.
【解答】解:(2+4+6+…+18+20)﹣(1+3+5+…17+19),
=2+4+6+…+18+20﹣1﹣3﹣5﹣…﹣17﹣19,
=(2﹣1)+(4﹣3)+(6﹣5)+…+(18﹣17)+(20﹣19),
=1+1+1+1+1+1+1+1+1+1,
=10.
【点评】本题的关键是根据连减的性质,把括号去掉,然后再根据加法交换律和结合律进一步解答即可.
7.为使加法计算更加简便,学习了加法交换律和 加法结合 律。根据这些运算定律,可以得知:650+258= 258 +650,261+ 92 +108=261+(92+108)
【分析】根据加法交换律a+b=b+a,加法结合律a+(b+c)=(a+b)+c,进行解答即可。
【解答】解:为使加法计算更加简便,学习了加法交换律和加法结合律。根据这些运算定律,可以得知:650+258=258+650,261+92+108=261+(92+108)。
故答案为:加法结合;258;92。
【点评】本题考查加法交换律和加法结合律的应用。注意计算的准确性。
8.小燕在计算36×(□+20)时,错算成了36×□+20,那么错误的结果比正确的结果 小 (填“大”或“小”),错误的结果与正确的结果相差 700 。
【分析】根据乘法分配律的意义,(a+b)×c=a×c+b×c,小燕在计算36×(□+20)时,错算成了36×□+20,显然错误结果比正确结果小,求出正确结果减去错误结果即可。
【解答】解:36×(□+20)
=36×□+36×20
=36×□+720
36×□+720﹣(36×□+20)
=36×□+720﹣36×□﹣20
=720﹣20
=700
答:错误的结果比正确的结果小,错误的结果与正确答案相差700。
故答案为:小,700。
【点评】此题先观察这两个算式的区别在什么地方,再对其中的一个变形,变成相接近的形式,进而求解。
9.(40+35)×50= 40 × 50 + 35 × 50 应用了 乘法分配 律,用字母表示为 (a+b)c=ac+bc 。
【分析】根据乘法分配律的意义,两个数的和与一个相乘,可以把两个加数分别与这个数相乘,然后把两个积相加,结果不变。据此解答。
【解答】解:(40+35)×50
=40×50+35×50
=2000+1750
=3750
应用了乘法分配律,用字母表示为:(a+b)c=ac+bc。
故答案为:40、50、35、50;乘法分配,(a+b)c=ac+bc。
【点评】此题考查的目的是理解掌握乘法分配律的意义及应用。
10.小刚的计算器上数字键“2”坏了,他要用计算器计算358×24,他可以怎样用这个计算器算出正确的结果?请写出2道不同的算式。 358×3×8 或 358×4×6 。
【分析】根据乘法的意义:358乘24,转化为358×3×8、358×4×6乘积,据此解答。
【解答】解:358×24,
转化为358×3×8、358×4×6乘积。
故答案为:358×3×8、358×4×6。
【点评】本题考查了数的拆分,关键吧24分成3与8、4与6的积,由此进行解答即可。
三.判断题(共5小题)
11.728+72﹣28=728﹣28+72。 √
【分析】加法交换律:两个加数交换位置,和不变。在同一级运算中,既可以按从左到右的运算顺序计算,也可交换﹣28与+72的位置,据此解答即可。
【解答】解:因为是同一级运算,可交换﹣28与+72的位置,所以728+72﹣28=728﹣28+72;所以原题说法正确。
故答案为:√。
【点评】此题重点考查了学生对加法交换律的掌握与运用情况。
12.a+b+c=b+(a+c)运用了加法交换律和加法结合律。 √
【分析】a+b+c=b+(a+c)是先交换了a和b的位置,然后把后两个加数结合在一起,由此求解。
【解答】解:a+b+c=b+(a+c)应用了加法交换律和加法结合律。原题说法正确。
故答案为:√。
【点评】①加法交换律:两个加数交换位置,和不变,如a+b=b+a;
②加法结合律:先把前两个数相加,或先把后两个数相加,和不变,如:a+b+c=a+(b+c)。
13.65+130+35+70=(65+35)+(130+70),只运用了加法交换律。 ×
【分析】根据加法交换律、加法结合律的意义,先运用加法交换律,再运用加法结合律简算。
【解答】解:65+130+35+70
=(65+35)+(130+70)
=100+200
=300
所以运用了加法交换律和加法结合律。
因此,题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解掌握加法交换律、加法结合律的意义,并且能够灵活运用加法交换律、加法结合律进行简算。
14.32×(7×3)=32×7+32×3. × .
【分析】本题应先算7×3,再与32相乘,不能用乘法分配律运算,因为不是32×(7+3)
【解答】解:32×(7×3)
=32×21
=672
不能运用乘法分配律来求解,因为不是32×(7+3)
所以题干的说法是错误的
故答案为:×
【点评】考查学生对乘法分配律的掌握情况.
15.(a×b)×c=a×(c×b). √ .
【分析】首先根据乘法结合律,可得(a×b)×c=a×(b×c);然后根据乘法交换律,可得a×(b×c)=a×(c×b),所以(a×b)×c=a×(c×b).
【解答】解:因为(a×b)×c=a×(c×b),
所以题中说法正确.
故答案为:√.
【点评】此题主要考查了运算定律与简便运算,要熟练掌握,注意乘法交换律和乘法结合律的应用.
四.计算题(共1小题)
16.简便运算。
208+106+192+194 8×(125+9)
56×99+56 25×37×4
【分析】(1)根据加法交换律和加法结合律简算;
(2)根据乘法分配律简算;
(3)根据乘法分配律简算;
(4)根据乘法交换律简算。
【解答】解:(1)208+106+192+194
=(208+192)+(106+194)
=400+300
=700
(2)8×(125+9)
=8×125+8×9
=1000+72
=1072
(3)56×99+56
=56×(99+1)
=56×100
=5600
(4)25×37×4
=25×4×37
=100×37
=3700
【点评】此题是考查四则混合运算,要仔细观察算式的特点,灵活运用一些定律进行简便计算。
五.应用题(共5小题)
17.
【分析】根据单价×数量=总价,可以运用乘法分配律,先求出买一件夹克衫和一条裤子需要多少元,再求出买4件夹克衫和4条裤子需要多少元,然后再加上一件短袖衫的价格即可。据此解答。
【解答】解:(65+45)×4+32
=110×4+32
=440+32
=472(元)
答:一共要付472元。
【点评】此题考查的目的是理解掌握单价、数量、总价三者之间的关系及应用,乘法分配律的意义及应用。
18.一只小猴喜欢吃香蕉,主人对它说:“每天早上吃三根,晚上吃四根。”小猴听了很生气。主人马上改口说:“那就早上吃四根,晚上吃三根吧!”小猴觉得自己占便宜了,很开心。对此,你是怎么想的?
【分析】猴子再精,也精不过主人。小猴每天早上吃的根数与晚上吃的根数之和,就是一天吃的根数,根据加法交换律,一天吃的根数不变。
【解答】解:3+4=4+3
小猴并没占到便宜,每天吃的根数不变。
【点评】此题是考查加法交换律的应用。交换两个加数的位置,和不变。
19.小玲每天早上要喝一盒牛奶,吃一个蛋糕。
【分析】根据题意,可以分别求出一个星期买牛奶花多少钱,买蛋糕花多少钱,然后合并起来,也可以根据乘法分配律,a×c+b×c=(a+b)×c,先求出一天买牛奶和蛋糕花多少钱,再求一个星期一共花多少钱。然后与30元进行比较即可,据此解答。
【解答】解:3×7+2×7
=21+14
=35(元)
或(3+2)×7
=5×7
=35(元)
30<35
答:不够。
【点评】此题考查的目的是理解整数乘法、加法的意义及应用,乘法分配律的意义及应用,整数大小比较的方法及应用。
20.实验小学图书室有8个书架,每个书架都有7层,每层可放125本书.这些书架一共可放多少本书?
【分析】先用每层放书的本数乘上7层,求出每个书架可以放几本书,再用每个书架放书的本数乘上8,即可求出8个书架可以放书的本数.
【解答】解:125×7×8
=125×8×7
=1000×7
=7000(本)
答:这些书架一共可放7000本书.
【点评】解决本题根据乘法的意义:求几个几是多少列出连乘算式求解即可.
21.四季超市运来大米和面粉各48袋,大米每袋75千克,面粉每袋25千克,一共运来大米和面粉共多少千克?
【分析】根据题意可知,大米的袋数×每袋大米的重量+面粉的袋数×每袋大米的重量=一共运来大米和面粉的总重量,依此列式并根据乘法分配律的特点进行计算即可。
【解答】解:48×75+48×25
=48×(75+25)
=48×100
=4800(千克)
答:一共运来大米和面粉共4800千克。
【点评】此题考查的是运用乘法分配律的特点解决实际问题,应熟练掌握。
一.选择题(共5小题)
1.与37×20的得数相等的算式是( )
A.20×37 B.27×20 C.2×37
【分析】乘法交换律:两个数相乘,交换因数的位置,积不变。用公式表示为:a×b=b×a。
【解答】解:37×20=20×37
故选:A。
【点评】本题利用具体的算式考查了学生对于乘法交换律的理解。
2.(2021春 河东区期末)506+720+280=506+(720+280)运用了( )
A.加法交换律 B.加法结合律
C.乘法分配律 D.加法交换律和结合律
【分析】根据加法结合律a+b+c=a+(b+c)进行解答即可。
【解答】解:506+720+280=506+(720+280)运用了加法结合律。
故选:B。
【点评】熟练地掌握加法结合律是解答本题的关键。
3.(2021春 钦州期末)下面算式中,( )所表示的不是加法交换律。
A.a+b=c+d B.20+a+b=a+b+20
C.a+x=x+a
【分析】根据加法交换律a+b=b+a进行解答即可。
【解答】解:A.a+b=c+d,表示的不是加法交换律;
B.20+a+b=a+b+20,表示的是加法交换律;
C.a+x=x+a,表示的是加法交换律。
故选:A。
【点评】熟练地掌握加法交换律是解答本题的关键。
4.(2022春 昆明月考)25×16与( )的结果相等。
A.25×10×6 B.25×4×4 C.25×10+6 D.20+5×16
【分析】因为25×4=100,所以把16分成4×4,则25×16=25×(4×4),再用乘法结合律,先算25×4=100,再算100×4即可解答。
【解答】解:25×16
=25×(4×4)
=25×4×4
=100×4
=400
答:25×16与25×4×4的结果相等。
故选:B。
【点评】本题考查了用乘法结合律灵活计算的能力。
5.(2022春 正安县期末)如果〇+ =10,那么78×〇+78× =( )
A.7800 B.780 C.78 D.无法确定
【分析】根据乘法分配律a×c+b×c=(a+b)×c进行解答即可。
【解答】解:78×〇+78×
=78×(〇+□)
=78×10
=780
故选:B。
【点评】熟练地掌握乘法分配律是解答本题的关键。
二.填空题(共5小题)
6.97+198+199+200+201+202+203+204= 1504 .
【分析】通过分析式中数据可以发现,只要把201、202、203、204分别写成200加一个一位数的形式,然后运用加法交换律和结合律,进行简算即可.
【解答】解:97+198+199+200+201+202+203+204,
=97+198+199+200+(200+1)+(200+2)+(200+3)+(200+4),
=97+198+199+200+200+1+200+2+200+3+200+4,
=(97+3)+(198+2)+(199+1)+200+200+200+200+200+4,
=100+200×7+4,
=1504.
故答案为:1504.
【点评】此题考查了加减法中的巧算,比较简单,只要认真观察,即可找到解题捷径.
7.(2022秋 顺德区期中)如果用字母a、b、c表示算式(49×125)×8=49×(125×8)中的三个数,那么算式中的规律可以写成 a×b×c=a×(b×c)
【分析】根据乘法结合律a×b×c=a×(b×c)进行解答即可。
【解答】解:(49×125)×8=49×(125×8),算式中的规律可以写成a×b×c=a×(b×c)。
故答案为:a×b×c=a×(b×c)。
【点评】本题主要考查了学生对乘法结合律的掌握。
8.(2022春 市中区期末)(100+2)×75=100×75+2×75,这里运用的运算律是 乘法分配律 ,用字母表示这个运算律是 (a+b)×c=a×c+b×c 。
【分析】根据乘法分配律(a+b)×c=a×c+b×c进行解答即可。
【解答】解:(100+2)×75=100×75+2×75,这里运用的运算律是乘法分配律,用字母表示这个运算律是(a+b)×c=a×c+b×c。
故答案为:乘法分配律,(a+b)×c=a×c+b×c。
【点评】熟练地掌握乘法分配律是解答本题的关键。
9.(2021秋 恩阳区 期末)360+ 92 +108=360+(92+ 108 )
【分析】根据加法结合律a+b+c=a+(b+c)进行解答即可。
【解答】解:360+92+108
=360+(92+108)
=360+200
=560
故答案为:92,108。
【点评】熟练地掌握加法结合律是解答本题的关键。
10.(2021秋 华州区期中)运用加法交换律和乘法交换律填一填。
279+135= 135 +279 72×138= 138 × 72
【分析】根据加法交换律、乘法交换律的意义,a+b=b+a,a×b=b×a,据此解答即可。
【解答】解:
279+135=135+279 72×138=138×72
故答案为:135,138,72。
【点评】此题考查的目的是理解掌握加法交换律、乘法交换律的意义及应用。
三.判断题(共5小题)
11.(2022秋 宁陕县期末)56×99=56×100﹣1 ×
【分析】根据题意,把99看作100﹣1,然后利用乘法的分配律解答.
【解答】解:56×99
=56×(100﹣1)
=56×100﹣1×56
=5600﹣56
=5544.
故答案为:×.
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.
12.25×(7×4)=(25×4)×7 √
【分析】根据乘法交换律a×b=b×a,乘法结合律a×b×c=a×(b×c)进行解答即可。
【解答】解:25×(7×4)
=(25×4)×7
=100×7
=700
所以原题干说法正确。
故答案为:√。
【点评】本题主要考查了学生对乘法交换律和结合律的掌握。
13.(2020秋 白云区期末)等式7bc=7(bc)是运用了乘法结合律。 √
【分析】乘法结合律:先乘前两个数,或先乘后两个数,积不变;用字母表示为:a×b×c=a×(b×c);据此解答。
【解答】解:由以上分析7bc=7(bc)运用了乘法结合律,所以原题干正确。
故答案为:√。
【点评】此题考查了学生对乘法结合律的掌握与运用。
14.(2022秋 上思县期末)整数的运算律对于分数同样适用。 √
【分析】整数加法、乘法的运算定律对于小数、分数同样适用。
【解答】解:整数加法的运算定律,对于分数同样适用,此说法正确。
故答案为:√。
【点评】此题考查的目的是使学生明确:整数加法、乘法的运算定律对于小数、分数同样适用。
15.(2022春 江汉区期末)54×70+54×28+2=54×(70+28+2)。 ×
【分析】根据乘法分配律的意义直接判断作答。
【解答】解:54×70+54×28+2
=54×(70+28)+2
=54×98+2
=54×100﹣54×2+2
=5400﹣108+2
=5294
原题说法错误。
故答案为:×。
【点评】解答本题的关键是熟记乘法分配律的公式:a×(b+c)=ab+ac。
四.计算题(共1小题)
16.(2021秋 临洮县期末)脱式计算,能简算的要简算。
720+[(12+24)×2] 25×48+25×52 (125+16)×8
75+149+51+125 8×56×125 87×101
【分析】(1)先算小括号里面的加法,再算中括号里面的乘法,最后算括号外的加法;
(2)根据乘法分配律简算;
(3)根据乘法分配律简算;
(4)根据加法交换律和加法结合律简算;
(5)根据乘法交换律简算;
(6)先把101分解成(100+1),再根据乘法分配律简算。
【解答】解:(1)720+[(12+24)×2]
=720+[36×2]
=720+72
=792
(2)25×48+25×52
=25×(48+52)
=25×100
=2500
(3)(125+16)×8
=125×8+16×8
=1000+128
=1128
(4)75+149+51+125
=(75+125)+(149+51)
=200+200
=400
(5)8×56×125
=8×125×56
=1000×56
=56000
(6)87×101
=87×(100+1)
=87×100+87×1
=8700+87
=8787
【点评】此题是考查四则混合运算,要仔细观察算式的特点,灵活运用一些定律进行简便计算。
五.应用题(共5小题)
17.(2022秋 怀柔区期末)请你结合生活中的事例,用你喜欢的方式(可以画图,也可以讲数学故事……),说说等10+7+13=10+(7+13)为什么成立。
【分析】10+7+13=10+(7+13)这是符合加法结合律的算式,可以举例说明加法结合律即可。
【解答】解:如图:三条线段的长度分别是10厘米,7厘米和13厘米,
那么三条线段的总长度可以表示为:
10+7+13=30(厘米)
也可以表示为:10+(7+13)=30(厘米)
所以:10+7+13=10+(7+13)。(答案不唯一)
【点评】本题考查了学生对于加法结合律的理解和应用。
18.(2022春 德州期中)乒乓球训练馆买了1200个乒乓球,每25个装一袋,每4袋装一盒,需要准备多少个盒子?(用简便方法来计算)
【分析】1200个乒乓球,每25个装一袋,用1200除以25求出1200里面有多少个25,就是可以装成多少袋,又每4袋装一盒,再用总袋数除以4,即可求出需要准备多少个盒子,计算时可以根据除法的性质计算。
【解答】解:1200÷25÷4
=1200÷(25×4)
=1200÷100
=12(个)
答:需要准备12个盒子。
【点评】解决本题根据除法的包含意义列出算式,再根据除法的计算性质进行简便运算。
19.(2022 南京模拟)小明从周一到周四每天踢毽子的次数如下:156下、195下、144下、205下。这四天他一共踢了多少下毽子?
【分析】求一共踢了多少下毽子,就是求和,把所有的加数相加156、195、144、205所得的和就是这四天他一共踢了多少下毽子。
【解答】解:156+195+144+205
=(156+144)+(195+205)
=300+400
=700(下)
答:这四天他一共踢了700下毽子。
【点评】本题考查了加法交换律和结合律的综合应用。
20.(2021春 汤阴县期中)同学们从学校到博物馆要走1200米,先走了236米到新华书店,又走了464米到人民广场,同学们还要走多少米才能到博物馆?
【分析】先用总路程减去236米,求出从新华书店道博物馆的路程,再减去464米,就是还要走的路程,计算时可以运用减法的性质进行简算。
【解答】解:1200﹣236﹣464
=1200﹣(236+464)
=1200﹣700
=500(米)
答:同学们还要走500米才能到博物馆。
【点评】解决本题也可以先求出已经走的路程,再用总路程减去已经走的路程即可;列式为1200﹣(236+464)。
21.(2022春 德州期中)学校食堂购进大米和面粉各204袋,大米每袋56元,面粉每袋44元。大米和面粉一共花了多少元?(用简便方法来计算)
【分析】大米每袋56元,204袋大米的价格就是204个56元,用56乘204即可求出大米的价格,同理求出面粉的价格,再相加即可,计算时根据乘法分配律简算。
【解答】解:56×204+44×204
=(56+44)×204
=100×204
=20400(元)
答:大米和面粉一共花了20400元。
【点评】解决本题根据乘法的意义列出算式,再根据乘法分配律简算。
