人教版九年级数学春学期开学考试测试题(含答案)
文档属性
| 名称 | 人教版九年级数学春学期开学考试测试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版九年级数学春学期开学考试测试题(含答案)
一、单选题:本大题共10小题,每小题3分,共30分。
1.如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得,若点在AB上,则的长为( )
A. B.4 C. D.5
2.二次函数与x轴交于(1,0)、(-3,0),则关于x的方程的解为( )
A.1,3 B.1,-5 C.-1,3 D.1,-3
3.下列不是一元二次方程的是( )
A. B. C. D.
4.2022年新能源车企迎来了更多的关注,如图是四款新能源汽车的标志,是中心对称图形的是( )
A. B.
C. D.
5.已知点、、在函数上,则、、的大小关系是( )
A. B.
C. D.
6.如图,已知四边形两条对角线相交于点,,,,则的值为( )
A.6 B.7 C.12 D.16
7.如图,,,,,过点作的平行线,为直线上一动点,为的外接圆,直线BP交于点,则的最小值为( )
A. B. C. D.1
8.如图,△ABC的边AC经过⊙O的圆心O,BC与⊙O相切于B,D是⊙O上的一点,连接AD,BD,若∠C=50°,则∠ADB的大小为( )
A.50° B.60° C.70° D.80°
9.如图,在矩形ABCD中,AB>AD,∠DAB的平分线与CD交于点E,过点C作CF⊥AE于点F,连接BF,DF.有下列结论:①DE=BC;②DF=BF;③∠CDF=∠CBF;④B,C,D,F四点在同一个圆上.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
10.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=1,以下4个结论,其中正确结论的是( )
A.abc>0 B.4a+2b+c=0
C.a+b>m(am+b) D.(a+c)2<b2
二、填空题:本大题共7小题,每小题4分,共28分。
11.点关于原点对称的点的坐标为 .
12. 关于的二次函数,在时有最大值6,则 .
13.已知抛物线y=ax2+bx+c(a≠0)经过点(﹣2,0),(0,4),对称轴在y轴右侧,有下列结论:
①a<0;
②0<b<2;
③关于x的方程ax2+bx+c=9始终有两个不等根;
④直线y=ax+c(a≠0)与抛物线y=ax2+bx+c(a≠0)始终有两个交点.
其中正确结论的序号为 .
14.若将抛物线y=﹣x2向左平移1个单位,再向下平移3个单位,则得到的抛物线的解析式是 .
15.如图,内接于,连接并延长交于点D,交于点E,若,则的长为 .
16.已知点,在抛物线的图象上,判断 .
17.已知方程有一个根是m,则代数式的值为 .
三、解答题:第18,19.20小题6分,第21,22,23小题9分,第24,25小题10分。
18.已知二次函数与轴只有1个交点,且经过点,求二次函数的表达式.
19.关于x的一元二次方程2(x﹣1)2+b(x﹣1)+c=0化为一般形式后为2x2﹣3x﹣1=0,试求b,c的值.
20.如图,在中,,在同一平面内,将绕点A旋转到的位置,使得∥,求的度数.
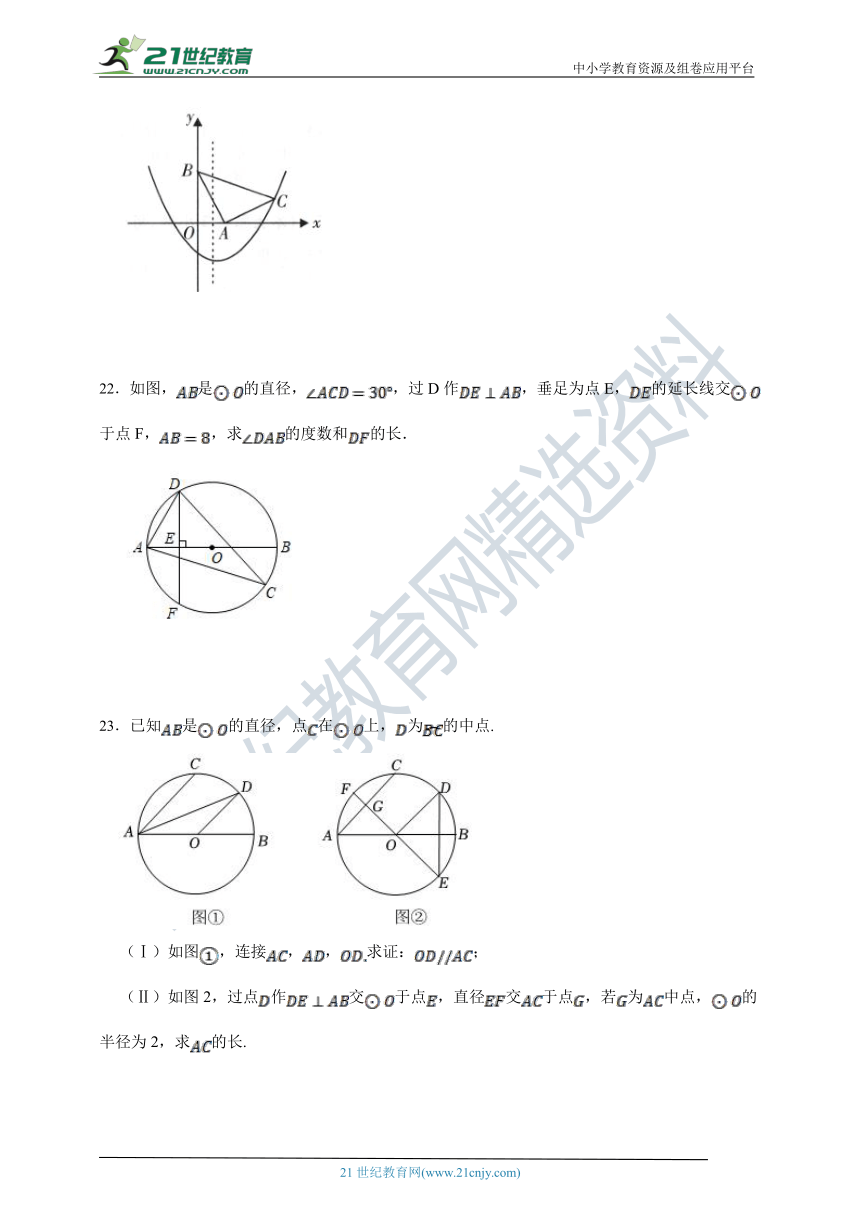
21.如图,在平面直角坐标系xOy中,OABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx-2过点C.求抛物线的表达式.
22.如图,是的直径,,过D作,垂足为点E,的延长线交于点F,,求的度数和的长.
23.已知是的直径,点在上,为的中点.
(Ⅰ)如图,连接,,求证:;
(Ⅱ)如图2,过点作交于点,直径交于点,若为中点,的半径为2,求的长.
24.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c的图象交x轴于A(4,0),B(﹣1,0)两点,交y轴于点C,连接AC.
(1)填空:该抛物线的函数解析式为 ,其对称轴为直线 ;
(2)若P是抛物线在第一象限内图象上的一动点,过点P作x轴的垂线,交AC于点Q,试求线段PQ的最大值;
(3)在(2)的条件下,当线段PQ最大时,在x轴上有一点E(不与点O,A重合),且EQ=EA,在x轴上是否存在点D,使得△ACD与△AEQ相似?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.
25.如图,在平面直角坐标系中,点O为坐标原点,抛物线y=x2+bx﹣3与x轴交于A,B两点,交y轴于点C,直线y=x+3交抛物线于A、D两点.
(1)求抛物线的解析式;
(2)若点P在抛物线上,连接AP、DP、BD,设点P的横坐标为t,若S△APD=S△ABD,求t的值.
(3)在(2)的条件下,若点P在第三象限,作直线PC,点E为y轴左侧抛物线上一点,过点作EF⊥PC于F,将△EFC绕点C顺时针旋转a,且tana=,若点E的对应点E'刚好落在坐标轴上,求点E的坐标.
参考答案
1. A2. D3. C4. C5. A6. B7. D8. C9. D10. D
11.(-1,5)
12. 2或
13.①②④
14. y=﹣ (x+1)2﹣3
15.
16. >
17. 2018
18.解:二次函数与轴只有1个交点,则,
即,
解得,
∴,
把代入得
∴,
∴.
19.解:2(x2﹣2x+1)+bx﹣b+c=0,
2x2+(b﹣4)x+2﹣b+c=0,
所以b﹣4=﹣3,2﹣b+c=﹣1,
解得b=1,c=﹣2.
20.解:∵∥且,
∴,
∵绕点A旋转到的位置,
∴,,
∴,
在中根据内角和定理即可得,
∴,
∴.
21.解:过点C作CD⊥x轴于点D,
则∠CAD+∠ACD= 90°,
∵∠OBA+∠OAB=90°,∠OAB+∠CAD=90°,
∴∠OAB=∠ACD,∠OBA=∠CAD,
又∵AB=AC,∴△AOB≌△CDA(ASA),∴CD=OA=1,AD=OB=2,
∴OD=OA+AD=3,∴点C的坐标为(3,1),
∵点C(3,1)在抛物线y= x2+bx-2上.∴1= ×9+3b-2,解得b= ,
∴抛物线的表达式为y= x2-x-2.
22.解:如图,连接,
∵,
∴,
∵是的直径,
∴,
∴;
∵,,
∴,
∵,,且是直径,
∴,,
∴,,
∴.
23.解:(Ⅰ)证明:如图连接,
为的中点,
,
,
,
,
,
;
(Ⅱ)如图,连接,
,为中点,
,
,
,
是的直径,,
,
,
,
,
是等腰直角三角形,
的半径为2,
,
.
24.(1);
(2)解:∵A(4,0),C(0,3),
∴直线AC的解析式为:
设,则
∴
∵P是抛物线在第一象限内图象上的一动点,
∴0∴当x=2时,PQ的最大值为3;
(3)解:不存在,点D的坐标为或( 4,0).
25.(1)解:直线y=x+3与x轴的交点A(﹣3,0),
将点A代入y=x2+bx﹣3,
∴9﹣3b﹣3=0,
解得b=2,
∴y=x2+2x﹣3
(2)解:令y=0,则x2+2x﹣3=0,
解得x=﹣3或x=1,
∴B(1,0),
当x2+2x﹣3=x+3时,解得x=2或x=﹣3,
∴D(2,5)
∴S△ABD= 4×5=10,
∵S△APD=S△ABD,
∴S△APD=10,
过点P作PG∥y轴交AD于点G,
∵点P的横坐标为t,
∴P(t,t2+2t﹣3),G(t,t+3),
∴PG=|t2+2t﹣3﹣t﹣3|=|t2+t﹣6|,
∴ |t2+t﹣6|×5=10,
解得t=﹣2或t=1(舍)或t= 或t= ,
∴t的值为﹣2或 或 ;
(3)解:∵P点在第三象限,
∴P(﹣2,﹣3),
∴CP∥x轴,
设E(m,m2+2m﹣3),则F(m,﹣3),
∴EF=m2+2m,FC=﹣m,
当E'点在x轴上时,过点F'作MN⊥x轴交于点M,交CF于点N,
∵∠FCF'=α,∠E'F'C=90°,
∴∠MF'E'=α,
∵tana= ,
∴MF'= E'F',NF'= CF',
∴ (m2+2m)+ (﹣m)=3,
解得m= 或m= (舍);
∴E( , );
当E'在y轴上时,过点E作EK⊥y轴交于点K,
由旋转可知∠ECE'=α,
∴ = ,
∴ = ,
解得m=﹣ 或m=0(舍),
∴E(﹣ , );
综上所述:E点坐标为( , )或(﹣ , )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学春学期开学考试测试题(含答案)
一、单选题:本大题共10小题,每小题3分,共30分。
1.如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得,若点在AB上,则的长为( )
A. B.4 C. D.5
2.二次函数与x轴交于(1,0)、(-3,0),则关于x的方程的解为( )
A.1,3 B.1,-5 C.-1,3 D.1,-3
3.下列不是一元二次方程的是( )
A. B. C. D.
4.2022年新能源车企迎来了更多的关注,如图是四款新能源汽车的标志,是中心对称图形的是( )
A. B.
C. D.
5.已知点、、在函数上,则、、的大小关系是( )
A. B.
C. D.
6.如图,已知四边形两条对角线相交于点,,,,则的值为( )
A.6 B.7 C.12 D.16
7.如图,,,,,过点作的平行线,为直线上一动点,为的外接圆,直线BP交于点,则的最小值为( )
A. B. C. D.1
8.如图,△ABC的边AC经过⊙O的圆心O,BC与⊙O相切于B,D是⊙O上的一点,连接AD,BD,若∠C=50°,则∠ADB的大小为( )
A.50° B.60° C.70° D.80°
9.如图,在矩形ABCD中,AB>AD,∠DAB的平分线与CD交于点E,过点C作CF⊥AE于点F,连接BF,DF.有下列结论:①DE=BC;②DF=BF;③∠CDF=∠CBF;④B,C,D,F四点在同一个圆上.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
10.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=1,以下4个结论,其中正确结论的是( )
A.abc>0 B.4a+2b+c=0
C.a+b>m(am+b) D.(a+c)2<b2
二、填空题:本大题共7小题,每小题4分,共28分。
11.点关于原点对称的点的坐标为 .
12. 关于的二次函数,在时有最大值6,则 .
13.已知抛物线y=ax2+bx+c(a≠0)经过点(﹣2,0),(0,4),对称轴在y轴右侧,有下列结论:
①a<0;
②0<b<2;
③关于x的方程ax2+bx+c=9始终有两个不等根;
④直线y=ax+c(a≠0)与抛物线y=ax2+bx+c(a≠0)始终有两个交点.
其中正确结论的序号为 .
14.若将抛物线y=﹣x2向左平移1个单位,再向下平移3个单位,则得到的抛物线的解析式是 .
15.如图,内接于,连接并延长交于点D,交于点E,若,则的长为 .
16.已知点,在抛物线的图象上,判断 .
17.已知方程有一个根是m,则代数式的值为 .
三、解答题:第18,19.20小题6分,第21,22,23小题9分,第24,25小题10分。
18.已知二次函数与轴只有1个交点,且经过点,求二次函数的表达式.
19.关于x的一元二次方程2(x﹣1)2+b(x﹣1)+c=0化为一般形式后为2x2﹣3x﹣1=0,试求b,c的值.
20.如图,在中,,在同一平面内,将绕点A旋转到的位置,使得∥,求的度数.
21.如图,在平面直角坐标系xOy中,OABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx-2过点C.求抛物线的表达式.
22.如图,是的直径,,过D作,垂足为点E,的延长线交于点F,,求的度数和的长.
23.已知是的直径,点在上,为的中点.
(Ⅰ)如图,连接,,求证:;
(Ⅱ)如图2,过点作交于点,直径交于点,若为中点,的半径为2,求的长.
24.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c的图象交x轴于A(4,0),B(﹣1,0)两点,交y轴于点C,连接AC.
(1)填空:该抛物线的函数解析式为 ,其对称轴为直线 ;
(2)若P是抛物线在第一象限内图象上的一动点,过点P作x轴的垂线,交AC于点Q,试求线段PQ的最大值;
(3)在(2)的条件下,当线段PQ最大时,在x轴上有一点E(不与点O,A重合),且EQ=EA,在x轴上是否存在点D,使得△ACD与△AEQ相似?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.
25.如图,在平面直角坐标系中,点O为坐标原点,抛物线y=x2+bx﹣3与x轴交于A,B两点,交y轴于点C,直线y=x+3交抛物线于A、D两点.
(1)求抛物线的解析式;
(2)若点P在抛物线上,连接AP、DP、BD,设点P的横坐标为t,若S△APD=S△ABD,求t的值.
(3)在(2)的条件下,若点P在第三象限,作直线PC,点E为y轴左侧抛物线上一点,过点作EF⊥PC于F,将△EFC绕点C顺时针旋转a,且tana=,若点E的对应点E'刚好落在坐标轴上,求点E的坐标.
参考答案
1. A2. D3. C4. C5. A6. B7. D8. C9. D10. D
11.(-1,5)
12. 2或
13.①②④
14. y=﹣ (x+1)2﹣3
15.
16. >
17. 2018
18.解:二次函数与轴只有1个交点,则,
即,
解得,
∴,
把代入得
∴,
∴.
19.解:2(x2﹣2x+1)+bx﹣b+c=0,
2x2+(b﹣4)x+2﹣b+c=0,
所以b﹣4=﹣3,2﹣b+c=﹣1,
解得b=1,c=﹣2.
20.解:∵∥且,
∴,
∵绕点A旋转到的位置,
∴,,
∴,
在中根据内角和定理即可得,
∴,
∴.
21.解:过点C作CD⊥x轴于点D,
则∠CAD+∠ACD= 90°,
∵∠OBA+∠OAB=90°,∠OAB+∠CAD=90°,
∴∠OAB=∠ACD,∠OBA=∠CAD,
又∵AB=AC,∴△AOB≌△CDA(ASA),∴CD=OA=1,AD=OB=2,
∴OD=OA+AD=3,∴点C的坐标为(3,1),
∵点C(3,1)在抛物线y= x2+bx-2上.∴1= ×9+3b-2,解得b= ,
∴抛物线的表达式为y= x2-x-2.
22.解:如图,连接,
∵,
∴,
∵是的直径,
∴,
∴;
∵,,
∴,
∵,,且是直径,
∴,,
∴,,
∴.
23.解:(Ⅰ)证明:如图连接,
为的中点,
,
,
,
,
,
;
(Ⅱ)如图,连接,
,为中点,
,
,
,
是的直径,,
,
,
,
,
是等腰直角三角形,
的半径为2,
,
.
24.(1);
(2)解:∵A(4,0),C(0,3),
∴直线AC的解析式为:
设,则
∴
∵P是抛物线在第一象限内图象上的一动点,
∴0
(3)解:不存在,点D的坐标为或( 4,0).
25.(1)解:直线y=x+3与x轴的交点A(﹣3,0),
将点A代入y=x2+bx﹣3,
∴9﹣3b﹣3=0,
解得b=2,
∴y=x2+2x﹣3
(2)解:令y=0,则x2+2x﹣3=0,
解得x=﹣3或x=1,
∴B(1,0),
当x2+2x﹣3=x+3时,解得x=2或x=﹣3,
∴D(2,5)
∴S△ABD= 4×5=10,
∵S△APD=S△ABD,
∴S△APD=10,
过点P作PG∥y轴交AD于点G,
∵点P的横坐标为t,
∴P(t,t2+2t﹣3),G(t,t+3),
∴PG=|t2+2t﹣3﹣t﹣3|=|t2+t﹣6|,
∴ |t2+t﹣6|×5=10,
解得t=﹣2或t=1(舍)或t= 或t= ,
∴t的值为﹣2或 或 ;
(3)解:∵P点在第三象限,
∴P(﹣2,﹣3),
∴CP∥x轴,
设E(m,m2+2m﹣3),则F(m,﹣3),
∴EF=m2+2m,FC=﹣m,
当E'点在x轴上时,过点F'作MN⊥x轴交于点M,交CF于点N,
∵∠FCF'=α,∠E'F'C=90°,
∴∠MF'E'=α,
∵tana= ,
∴MF'= E'F',NF'= CF',
∴ (m2+2m)+ (﹣m)=3,
解得m= 或m= (舍);
∴E( , );
当E'在y轴上时,过点E作EK⊥y轴交于点K,
由旋转可知∠ECE'=α,
∴ = ,
∴ = ,
解得m=﹣ 或m=0(舍),
∴E(﹣ , );
综上所述:E点坐标为( , )或(﹣ , )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
