人教版八年级数学春学期开学考试测试题(含答案)
文档属性
| 名称 | 人教版八年级数学春学期开学考试测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 11:22:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级数学春学期开学考试测试题(含答案)
一、单选题:本大题共10小题,每小题3分,共30分。
1.若分式的值为零,则x的值是( )
A.1 B.-1 C.±1 D.2
2.对于①,②,从左到右的变形,表述正确的是( )
A.①是因式分解,②是乘法运算 B.①是乘法运算,②是因式分解
C.①②都是因式分解 D.①②都是乘法运算
3.已知时,分式无意义,则“□”可以是( )
A. B. C. D.
4.周末李强和朋友到森林公园游玩,为测量园内湖岸A,B两点之间的距离,如图,李强在湖的一侧选取了一点O,测得OA=20m,OB=8m,则A,B间的距离可能是( )
A.10m B.22m C.30m D.32m
5.如图,已知BF=DE,AB∥DC,要使△ABF≌△CDE,添加的条件可以是( )
A.BE=DF B.AF=CE C.AB=CD D.∠B=∠D
6.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点P、Q,作直线PQ交AB于点D,连接AD,若△ABC的周长为15,AB=6,则△ADC的周长为( )
A.6 B.7 C.8 D.9
7.在△ABC中,AB=2,BC=3,AC的长不可能的是( )
A.1 B.2 C.3 D.4
8.已知Rt△ABC≌Rt△EDF,Rt△ABC的面积为12,Rt△EDF的一条直角边等于3,则另一直角边的长是( )
A.2 B.4 C.6 D.8
9.点关于x轴对称的点的坐标为( )
A. B. C. D.
10.如图,在△ABC中,AD是△ABC的角平分线,则( )
A.∠1=∠BAC B.∠1=∠ABC C.∠1=∠BAC D.∠1=∠ABC
二、填空题:本大题共7小题,每小题4分,共28分。
11.如图,在中,是的垂直平分线,3cm,的周长为12cm,则的周长是 .
12.如图,某小区广场有两个长度相等的滑梯靠在一面墙上,已知左边滑梯水平方向的长度AB与右边滑梯的高度DE相等.若右边滑梯与地面的夹角∠DFE=55°,则∠ABC的度数为 °.
13.若分式的值为零,则a的值是 .
14.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获.如图是由一副三角板拼凑得到的,图中∠1= °.
15.如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是 .
16.已知点和点关于轴对称,那么a+b= .
17.在平面直角坐标系中,点关于轴的对称点在第 象限.
三、解答题:第18,19.20小题6分,第21,22,23小题9分,第24,25小题10分。
18.先化简,再求值:(a+)÷,其中a=﹣2,b=3.
19.“油纸伞”是汉族古老的传统工艺品之一(如图1),其制作工艺十分巧妙.如图2,伞圈D沿着伞柄AP滑动时,总有伞骨AB=AC,BD=CD.问:伞柄AP是否始终平分同一平面内两条伞骨所成的∠BAC?请说明理由.
20.如图,,,,平分,若,求的长.
21.列方程解应用题:某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所用时间与原计划生产450台机器所需时间相同,现在平均每天生产多少台机器?
22.在一次数学课上,张老师在屏幕上出示了一个例题:
如图,在△ABC中,D、E分别是AB、AC上的一点,BE与CD交于点O,给出下列四个条件:①BD=CE;②∠BDO=∠CEO;③OB=OC;④∠DBO=∠ECO.要求从这四个等式中选出两个作为已知条件,可判定AB=AC.请写出你的选择,并证明.
23.如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一动点,延长BD交CE于E,且CE⊥BD,若BD平分∠ABC,求证:CE= BD
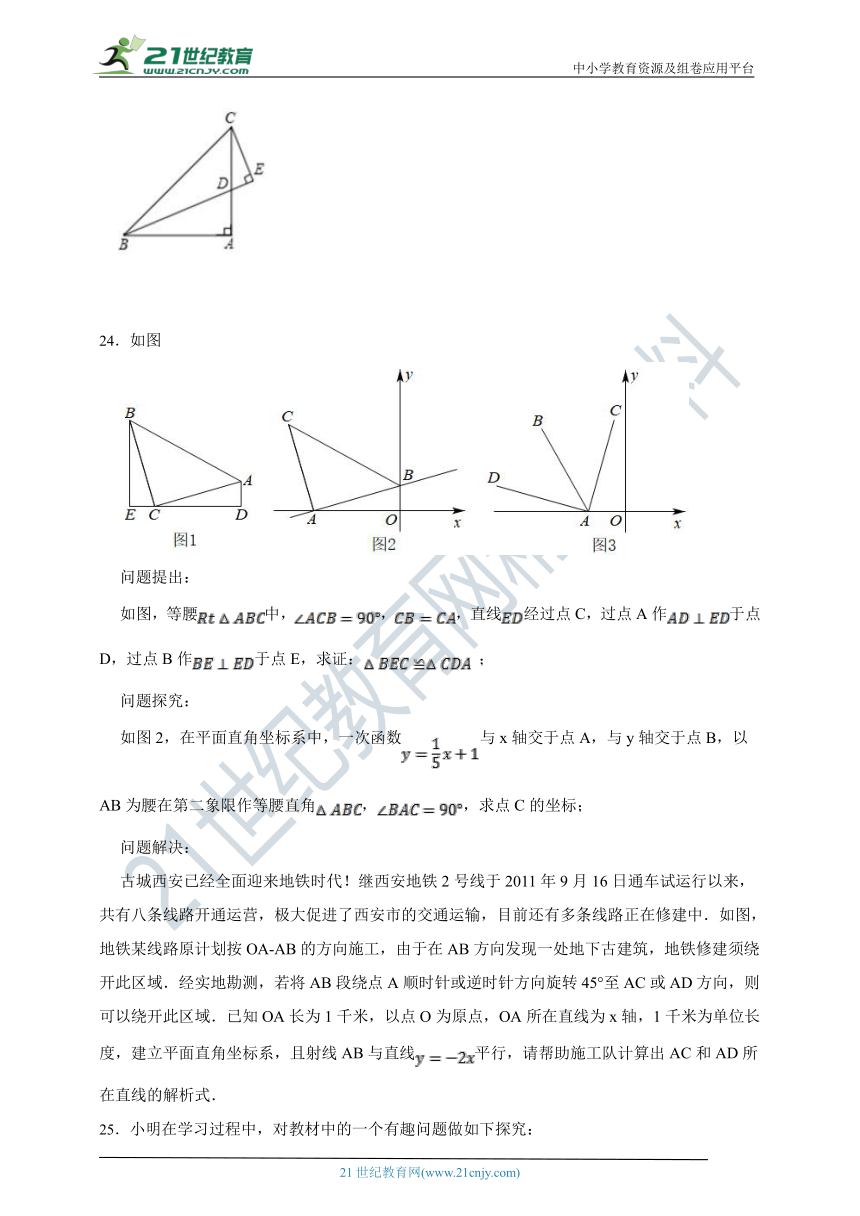
24.如图
问题提出:
如图,等腰中,,,直线经过点C,过点A作于点D,过点B作于点E,求证: ;
问题探究:
如图2,在平面直角坐标系中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角,,求点C的坐标;
问题解决:
古城西安已经全面迎来地铁时代!继西安地铁2号线于2011年9月16日通车试运行以来,共有八条线路开通运营,极大促进了西安市的交通运输,目前还有多条线路正在修建中.如图,地铁某线路原计划按OA-AB的方向施工,由于在AB方向发现一处地下古建筑,地铁修建须绕开此区域.经实地勘测,若将AB段绕点A顺时针或逆时针方向旋转45°至AC或AD方向,则可以绕开此区域.已知OA长为1千米,以点O为原点,OA所在直线为x轴,1千米为单位长度,建立平面直角坐标系,且射线AB与直线平行,请帮助施工队计算出AC和AD所在直线的解析式.
25.小明在学习过程中,对教材中的一个有趣问题做如下探究:
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由。
答案
1. A2. A3. C4. B5. C6. D7. A8. D9. A10. A
11. 18cm
12. 35
13. 2
14. 105
15. 18cm
16. -10
17.三
18.解:原式==a+b,
当a=﹣2,b=3时,原式=1.
19.解:AP平分∠BAC,
理由如下:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AP平分∠BAC.
20.解:∵,
∴
∵平分
∴
∴
∴
∵,
∴
21.解:设该工厂原来平均每天生产x台机器,则现在平均每天生产(x+50)台机器.依题意得:
解得:x=150.
经检验知,x=150是原方程的根.
所以现在平均每天生产200台机器.
答:现在平均每天生产200台机器.
22.证明:③④作为已知条件
证明如下:
∵ OB=OC,
∴ ∠OBC=∠OCB,
∵ ∠DBO=∠ECO,
∴ ∠DBC=∠ECB,
∴ AB=AC.
23.证明:延长CE、BA交于点F.
∵CE⊥BD于E,∠BAC=90°,
∴∠ABD=∠ACF.
在△ABD与△ACF中,
∵ ,
∴△ABD≌△ACF(ASA),
∴BD=CF.
∵BD平分∠ABC,
∴∠CBE=∠FBE.
在△BCE与△BFE中,
∵ ,
∴△BCE≌△BFE(ASA),
∴CE=EF,
即CE= CF,
∴CE= BD.
24.解:问题提出:
证明:∵,,
∴,
∴,
∵,
∴,
∴,
在和中
,
∴(AAS);
问题探究:
解:,
当时:;
当时:;
∴,,
∴,
过点作轴,交轴与点,
同上法可证:(AAS),
∴,
∴,
∴;
问题解决:
解:由题意得:,
∵射线AB与直线平行,
设直线的解析式为:,
则:,解得:;
∴;
延长交轴与点,延长至点,使,设,过点分别作轴,
由问题提出可知:(AAS),
∴,
∴,
∴的中点坐标为:,
由题意可知在直线AB上,
∴,
解得:,
∴,,
设的解析式为:,
则:,
解得:,
∴;
设的解析式为:,
则:,
解得:,
∴;
25.解:【习题回顾】证明:∵∠ACB=90°,CD是高,
∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,
∴∠B=∠ACD,
∵AE是角平分线,
∴∠CAF=∠DAF,
∵∠CFE=∠CAF+∠ACD,
∠CEF=∠DAF+∠B,
∴∠CEF=∠CFE;
【变式思考】∠CEF=∠CFE
证明:∵AF为∠BAG的角平分线,
∴∠GAF=∠DAF,
∵CD为AB边上的高,
∴∠ADC=90°,
∴∠ADF=∠ACE=90°,又∵∠CAE=∠GAF,
∴∠CEF=∠CFE;
【探究延伸】∠M+∠CFE=90°,
证明:∵C、A、G三点共线 AE、AN为角平分线,
∴∠EAN=90°,又∵∠GAN=∠CAM,
∴∠M+∠CEF=90°,
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,
∴∠CEF=∠CFE,
∴∠M+∠CFE=90°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学春学期开学考试测试题(含答案)
一、单选题:本大题共10小题,每小题3分,共30分。
1.若分式的值为零,则x的值是( )
A.1 B.-1 C.±1 D.2
2.对于①,②,从左到右的变形,表述正确的是( )
A.①是因式分解,②是乘法运算 B.①是乘法运算,②是因式分解
C.①②都是因式分解 D.①②都是乘法运算
3.已知时,分式无意义,则“□”可以是( )
A. B. C. D.
4.周末李强和朋友到森林公园游玩,为测量园内湖岸A,B两点之间的距离,如图,李强在湖的一侧选取了一点O,测得OA=20m,OB=8m,则A,B间的距离可能是( )
A.10m B.22m C.30m D.32m
5.如图,已知BF=DE,AB∥DC,要使△ABF≌△CDE,添加的条件可以是( )
A.BE=DF B.AF=CE C.AB=CD D.∠B=∠D
6.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点P、Q,作直线PQ交AB于点D,连接AD,若△ABC的周长为15,AB=6,则△ADC的周长为( )
A.6 B.7 C.8 D.9
7.在△ABC中,AB=2,BC=3,AC的长不可能的是( )
A.1 B.2 C.3 D.4
8.已知Rt△ABC≌Rt△EDF,Rt△ABC的面积为12,Rt△EDF的一条直角边等于3,则另一直角边的长是( )
A.2 B.4 C.6 D.8
9.点关于x轴对称的点的坐标为( )
A. B. C. D.
10.如图,在△ABC中,AD是△ABC的角平分线,则( )
A.∠1=∠BAC B.∠1=∠ABC C.∠1=∠BAC D.∠1=∠ABC
二、填空题:本大题共7小题,每小题4分,共28分。
11.如图,在中,是的垂直平分线,3cm,的周长为12cm,则的周长是 .
12.如图,某小区广场有两个长度相等的滑梯靠在一面墙上,已知左边滑梯水平方向的长度AB与右边滑梯的高度DE相等.若右边滑梯与地面的夹角∠DFE=55°,则∠ABC的度数为 °.
13.若分式的值为零,则a的值是 .
14.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获.如图是由一副三角板拼凑得到的,图中∠1= °.
15.如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是 .
16.已知点和点关于轴对称,那么a+b= .
17.在平面直角坐标系中,点关于轴的对称点在第 象限.
三、解答题:第18,19.20小题6分,第21,22,23小题9分,第24,25小题10分。
18.先化简,再求值:(a+)÷,其中a=﹣2,b=3.
19.“油纸伞”是汉族古老的传统工艺品之一(如图1),其制作工艺十分巧妙.如图2,伞圈D沿着伞柄AP滑动时,总有伞骨AB=AC,BD=CD.问:伞柄AP是否始终平分同一平面内两条伞骨所成的∠BAC?请说明理由.
20.如图,,,,平分,若,求的长.
21.列方程解应用题:某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所用时间与原计划生产450台机器所需时间相同,现在平均每天生产多少台机器?
22.在一次数学课上,张老师在屏幕上出示了一个例题:
如图,在△ABC中,D、E分别是AB、AC上的一点,BE与CD交于点O,给出下列四个条件:①BD=CE;②∠BDO=∠CEO;③OB=OC;④∠DBO=∠ECO.要求从这四个等式中选出两个作为已知条件,可判定AB=AC.请写出你的选择,并证明.
23.如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一动点,延长BD交CE于E,且CE⊥BD,若BD平分∠ABC,求证:CE= BD
24.如图
问题提出:
如图,等腰中,,,直线经过点C,过点A作于点D,过点B作于点E,求证: ;
问题探究:
如图2,在平面直角坐标系中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角,,求点C的坐标;
问题解决:
古城西安已经全面迎来地铁时代!继西安地铁2号线于2011年9月16日通车试运行以来,共有八条线路开通运营,极大促进了西安市的交通运输,目前还有多条线路正在修建中.如图,地铁某线路原计划按OA-AB的方向施工,由于在AB方向发现一处地下古建筑,地铁修建须绕开此区域.经实地勘测,若将AB段绕点A顺时针或逆时针方向旋转45°至AC或AD方向,则可以绕开此区域.已知OA长为1千米,以点O为原点,OA所在直线为x轴,1千米为单位长度,建立平面直角坐标系,且射线AB与直线平行,请帮助施工队计算出AC和AD所在直线的解析式.
25.小明在学习过程中,对教材中的一个有趣问题做如下探究:
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由。
答案
1. A2. A3. C4. B5. C6. D7. A8. D9. A10. A
11. 18cm
12. 35
13. 2
14. 105
15. 18cm
16. -10
17.三
18.解:原式==a+b,
当a=﹣2,b=3时,原式=1.
19.解:AP平分∠BAC,
理由如下:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AP平分∠BAC.
20.解:∵,
∴
∵平分
∴
∴
∴
∵,
∴
21.解:设该工厂原来平均每天生产x台机器,则现在平均每天生产(x+50)台机器.依题意得:
解得:x=150.
经检验知,x=150是原方程的根.
所以现在平均每天生产200台机器.
答:现在平均每天生产200台机器.
22.证明:③④作为已知条件
证明如下:
∵ OB=OC,
∴ ∠OBC=∠OCB,
∵ ∠DBO=∠ECO,
∴ ∠DBC=∠ECB,
∴ AB=AC.
23.证明:延长CE、BA交于点F.
∵CE⊥BD于E,∠BAC=90°,
∴∠ABD=∠ACF.
在△ABD与△ACF中,
∵ ,
∴△ABD≌△ACF(ASA),
∴BD=CF.
∵BD平分∠ABC,
∴∠CBE=∠FBE.
在△BCE与△BFE中,
∵ ,
∴△BCE≌△BFE(ASA),
∴CE=EF,
即CE= CF,
∴CE= BD.
24.解:问题提出:
证明:∵,,
∴,
∴,
∵,
∴,
∴,
在和中
,
∴(AAS);
问题探究:
解:,
当时:;
当时:;
∴,,
∴,
过点作轴,交轴与点,
同上法可证:(AAS),
∴,
∴,
∴;
问题解决:
解:由题意得:,
∵射线AB与直线平行,
设直线的解析式为:,
则:,解得:;
∴;
延长交轴与点,延长至点,使,设,过点分别作轴,
由问题提出可知:(AAS),
∴,
∴,
∴的中点坐标为:,
由题意可知在直线AB上,
∴,
解得:,
∴,,
设的解析式为:,
则:,
解得:,
∴;
设的解析式为:,
则:,
解得:,
∴;
25.解:【习题回顾】证明:∵∠ACB=90°,CD是高,
∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,
∴∠B=∠ACD,
∵AE是角平分线,
∴∠CAF=∠DAF,
∵∠CFE=∠CAF+∠ACD,
∠CEF=∠DAF+∠B,
∴∠CEF=∠CFE;
【变式思考】∠CEF=∠CFE
证明:∵AF为∠BAG的角平分线,
∴∠GAF=∠DAF,
∵CD为AB边上的高,
∴∠ADC=90°,
∴∠ADF=∠ACE=90°,又∵∠CAE=∠GAF,
∴∠CEF=∠CFE;
【探究延伸】∠M+∠CFE=90°,
证明:∵C、A、G三点共线 AE、AN为角平分线,
∴∠EAN=90°,又∵∠GAN=∠CAM,
∴∠M+∠CEF=90°,
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,
∴∠CEF=∠CFE,
∴∠M+∠CFE=90°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
