2022—2023学年人教版数学八年级上册 11.3.2多边形的内角和解答题 (无答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册 11.3.2多边形的内角和解答题 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 73.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 09:29:38 | ||
图片预览

文档简介
11.3.2多边形的内角和(解答题)
姓名: 得分: 日期:
1、如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A′处,折痕为DE.已知∠BDA′=110°,∠C=70°,∠B=80°,设∠CFD=α,∠CEA′=β,求α和β的大小.
2、在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
3、一个正多边形的每个外角是45°.
(1)试求这个多边形的边数;
(2)求这个多边形内角和的度数.
4、一个多边形的内角和是它的外角和的5倍,求这个多边形的边数.
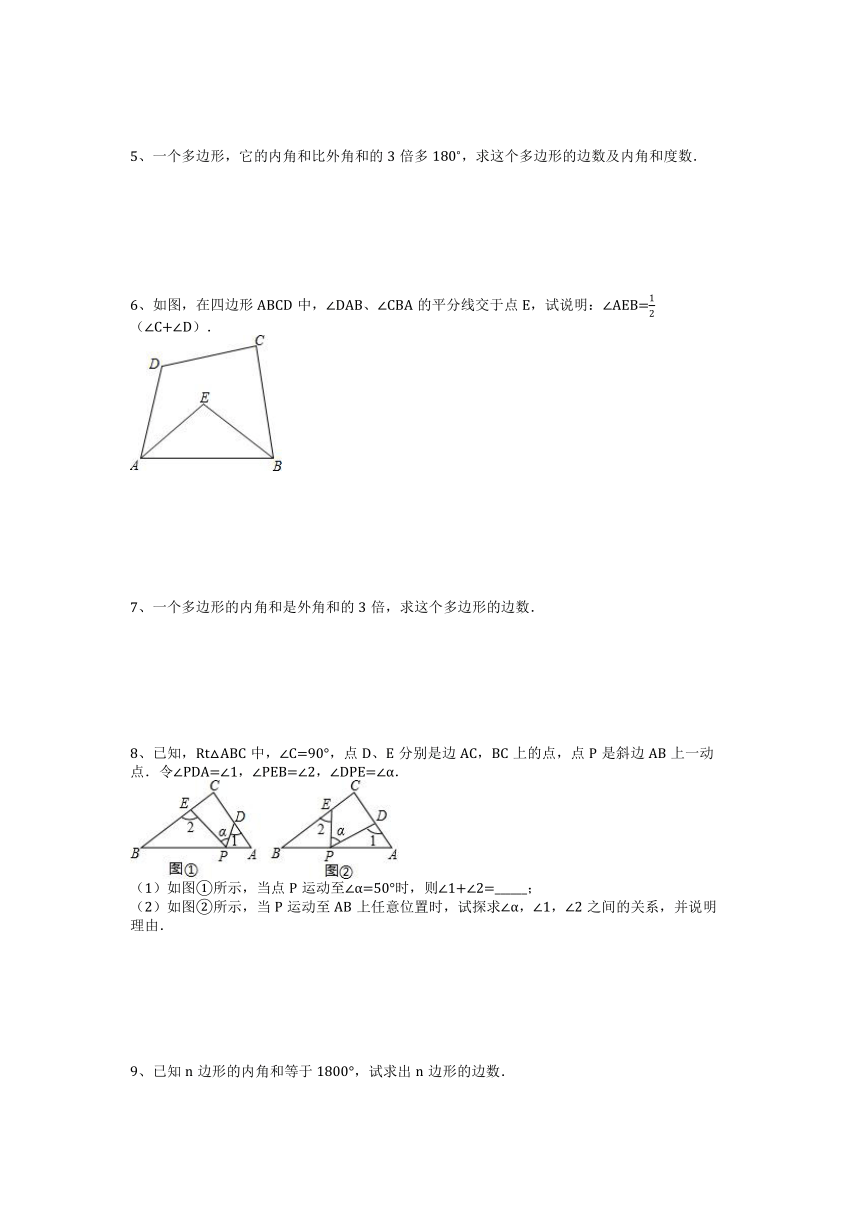
5、一个多边形,它的内角和比外角和的3倍多 ,求这个多边形的边数及内角和度数.
6、如图,在四边形ABCD中,∠DAB、∠CBA的平分线交于点E,试说明:∠AEB= (∠C+∠D).
7、一个多边形的内角和是外角和的3倍,求这个多边形的边数.
8、已知,Rt△ABC中,∠C=90°,点D、E分别是边AC,BC上的点,点P是斜边AB上一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)如图①所示,当点P运动至∠α=50°时,则∠1+∠2=______;
(2)如图②所示,当P运动至AB上任意位置时,试探求∠α,∠1,∠2之间的关系,并说明理由.
9、已知n边形的内角和等于1800°,试求出n边形的边数.
10、一个多边形的内角和与外角和的和是1440°,通过计算说明它是几边形.
11、一个多边形内角和的度数比外角和的度数的4倍多180度,求多边形的边数.
12、四边形ABCD中,∠A=140°,∠D=80度.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
13、如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
14、(1)某多边形的内角和与外角和的总和为 ,求此多边形的边数;
(2)某多边形的每一个内角都等于 ,求这个多边形的内角和.
15、如图1,在△ABC中,∠A=80°,BD、CE分别平分∠ABC、∠ACB,BD与CE交于点F.
(1)求∠BFC的度数;
(2)如图2,EG、DG分别平分∠AEF、∠ADF,EG与DG交于点G,求∠EGD的度数.
16、如图所示,求∠A+∠B+∠C+∠D+∠E+∠F.
17、探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:______.
18、如图,在六边形ABCDEF中,AF∥CD,AB∥DE,且∠A=120°,∠B=80°,求∠C和∠D的度数.
姓名: 得分: 日期:
1、如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A′处,折痕为DE.已知∠BDA′=110°,∠C=70°,∠B=80°,设∠CFD=α,∠CEA′=β,求α和β的大小.
2、在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
3、一个正多边形的每个外角是45°.
(1)试求这个多边形的边数;
(2)求这个多边形内角和的度数.
4、一个多边形的内角和是它的外角和的5倍,求这个多边形的边数.
5、一个多边形,它的内角和比外角和的3倍多 ,求这个多边形的边数及内角和度数.
6、如图,在四边形ABCD中,∠DAB、∠CBA的平分线交于点E,试说明:∠AEB= (∠C+∠D).
7、一个多边形的内角和是外角和的3倍,求这个多边形的边数.
8、已知,Rt△ABC中,∠C=90°,点D、E分别是边AC,BC上的点,点P是斜边AB上一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)如图①所示,当点P运动至∠α=50°时,则∠1+∠2=______;
(2)如图②所示,当P运动至AB上任意位置时,试探求∠α,∠1,∠2之间的关系,并说明理由.
9、已知n边形的内角和等于1800°,试求出n边形的边数.
10、一个多边形的内角和与外角和的和是1440°,通过计算说明它是几边形.
11、一个多边形内角和的度数比外角和的度数的4倍多180度,求多边形的边数.
12、四边形ABCD中,∠A=140°,∠D=80度.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
13、如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
14、(1)某多边形的内角和与外角和的总和为 ,求此多边形的边数;
(2)某多边形的每一个内角都等于 ,求这个多边形的内角和.
15、如图1,在△ABC中,∠A=80°,BD、CE分别平分∠ABC、∠ACB,BD与CE交于点F.
(1)求∠BFC的度数;
(2)如图2,EG、DG分别平分∠AEF、∠ADF,EG与DG交于点G,求∠EGD的度数.
16、如图所示,求∠A+∠B+∠C+∠D+∠E+∠F.
17、探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:______.
18、如图,在六边形ABCDEF中,AF∥CD,AB∥DE,且∠A=120°,∠B=80°,求∠C和∠D的度数.
