一元二次方程根与系数的关系 课件

课件17张PPT。宝剑锋从磨砺出，梅花香自苦寒来！十年寒窗无人问，一举成名天下知！一元二次方程根与系数的关系引领人：雪野中学 亓燕1.一元二次方程的一般形式是什么？2.一元二次方程的求根公式是什么？回忆1、熟练掌握一元二次方程根与系数的关系。
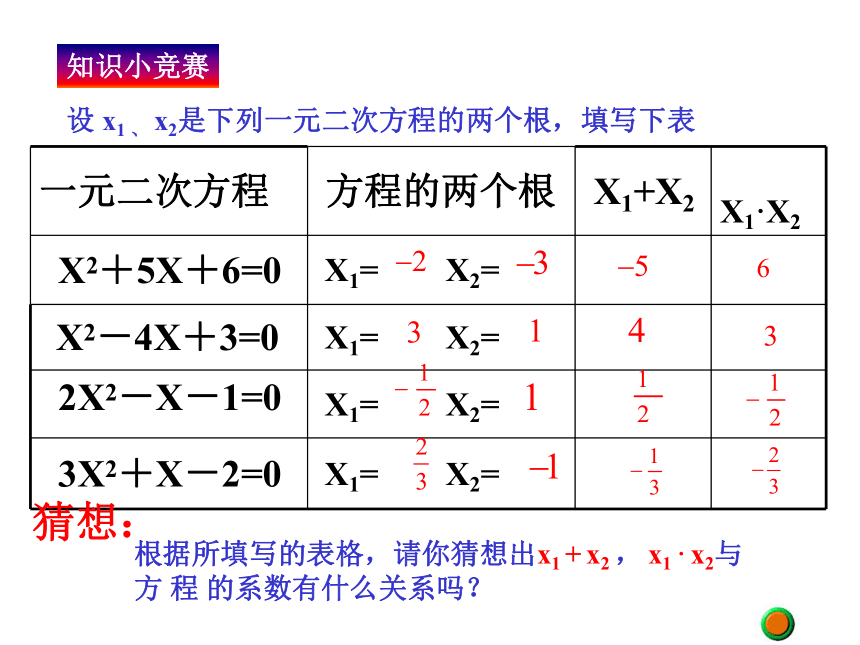
2、灵活运用一元二次方程根与系数的关系解决实际问题。学习目标知识小竞赛设 x1 、 x2是下列一元二次方程的两个根，填写下表猜想：根据所填写的表格，请你猜想出x1 + x2 ， x1 · x2与 方 程 的系数有什么关系吗？ 小组活动一：证明你们的猜想已知：如果一元二次方程
的两个根分别是 、 。求证：已知：如果一元二次方程
的两个根分别是 、 。已知：如果一元二次方程
的两个根分别是 、 。已知：如果一元二次方程
的两个根分别是 、 。已知：如果一元二次方程
的两个根分别是 、 。已知：如果一元二次方程
的两个根分别是 、 。已知：如果一元二次方程
的两个根分别是 、 。已知：如果一元二次方程
的两个根分别是 、 。已知：如果一元二次方程
的两个根分别是 、 。求证：已知：如果一元二次方程
的两个根分别是 、 。求证：已知：如果一元二次方程
的两个根分别是 、 。证明：　　　对任意的一元二次方程，它的两根之和与两根之积与方程的系数都有这样的关系存在，就是　　　　　　
　　　　　　
　　　
此定理是法国数学家韦达首先发现的，也称为韦达定理
归纳我能行当堂达标（一）技能训练3.已知方程2x2 ＋ 4x － 3 ＝ 0的两个根是 ，请完成下列问题：
（1）. （2）.
（3）. （4）.
（5）.
推论：当堂达标（二）思考题：
（1）你能写出一个一元二次方程，使它的两个根是1、2吗？
例2.已知方程x2-(k+1)x+3k=0的一个根是2,求另一根及k的值.解：设另一根为m解法一：将x=2代入方程，4-2(k+1)+3k=0 , k=2 ,
由根与系数关系2m=3k , m=-3变式训练
已知关于x的方程x2 ＋ px＋2＝0的两个根之和为－3，求 p 及两根的值 ；
已知关于x的方程x2-(2k-1)x+k2-k=0的两个根恰好等于斜边为5的直角三角形的两条直角边的长,求实数k的值.小结：以小组为单位畅所欲言自己本节课的收获！谢谢大家，欢迎批评指正，多提宝贵意见。作业：选做题：2.不解方程，求方程3x2+2x-6=0的两根
(1) 倒数和，(2)平方和，(3)平方差.必做题：1.课本P57 习题 2.