山东省泰安市岱岳区2014届九年级上学期期末数学试题(WORD版)
文档属性
| 名称 | 山东省泰安市岱岳区2014届九年级上学期期末数学试题(WORD版) |

|
|
| 格式 | zip | ||
| 文件大小 | 328.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-17 00:00:00 | ||
图片预览


文档简介
山东省泰安市岱岳区2014届九年级(上)期末数学试卷
一、选择题(本大题共16小题,每小题3分,共48分)
1.已知⊙O1与⊙O2相切,⊙O1的半径为3cm,⊙O2的半径为2cm,则O1O2的长是( )
A. 1cm B. 5cm C. 1cm或5cm D. 0.5cm或2.5cm
2.如图,点A,B,C在⊙O上,∠A=50°,则∠BOC的度数为( )
A. 40° B. 50° C. 80° D. 100°
3.二次函数y=ax2+bx+c图象上部分点的坐标满足下表:
x … ﹣3 ﹣2 ﹣1 0 1 …
y … ﹣3 ﹣2 ﹣3 ﹣6 ﹣11 …
则该函数图象的顶点坐标为( )
A. (﹣3,﹣3) B. (﹣2,﹣2) C. (﹣1,﹣3) D. (0,﹣6)
4. 2013年“五 一”期间,小明与小亮两家准备从东营港、黄河入海口、龙悦湖中选择一景点游玩,小明与小亮通过抽签方式确定景点,则两家抽到同一景点的概率是( )
A. B. C. D.
5.将二次函数y=x2的图象向右平移一个单位长度,再向上平移3个单位长度所得的图象解析式为( )
A. y=(x﹣1)2+3 B. y=(x+1)2+3 C. y=(x﹣1)2﹣3 D. y=(x+1)2﹣3
6.反比例函数y=的图象如图所示,以下结论:
①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
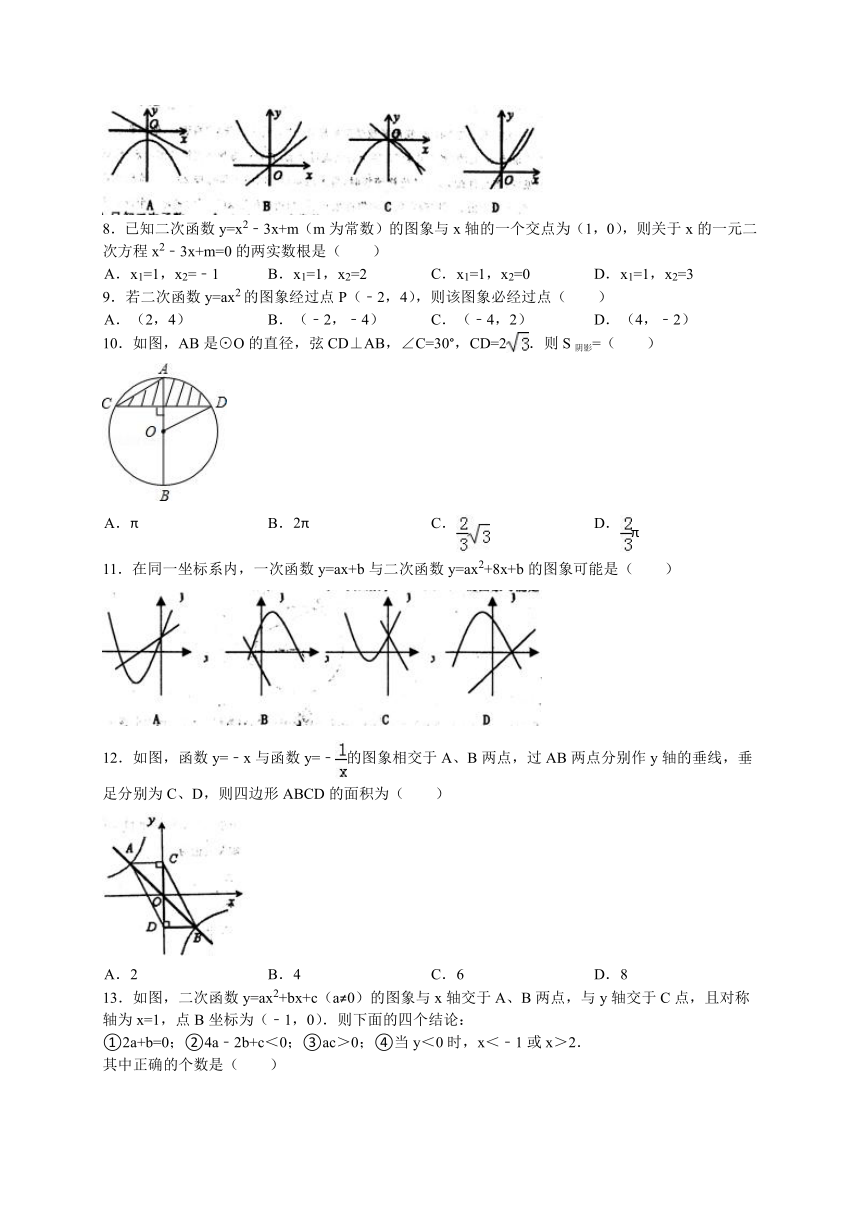
7.若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )
8.已知二次函数y=x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣3x+m=0的两实数根是( )
A. x1=1,x2=﹣1 B. x1=1,x2=2 C. x1=1,x2=0 D. x1=1,x2=3
9.若二次函数y=ax2的图象经过点P(﹣2,4),则该图象必经过点( )
A. (2,4) B. (﹣2,﹣4) C. (﹣4,2) D. (4,﹣2)
10.如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2.则S阴影=( )
A. π B. 2π C. D. π
11.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
12.如图,函数y=﹣x与函数y=﹣的图象相交于A、B两点,过AB两点分别作y轴的垂线,垂足分别为C、D,则四边形ABCD的面积为( )
A. 2 B. 4 C. 6 D. 8
13.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.
其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
14.绍兴是著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )
A. 4m B. 5m C. 6m D. 8m
15.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A. 30° B. 45° C. 60° D. 90°
16.如图,直线y=与双曲线y=(k>0,x>0)交于点A,将直线y=向上平移4个单位长度后,与y轴交于点C,与双曲线y=(k>0,x>0)交于点B,若OA=3BC,则k的值为( )
A. 3 B. 6 C. D.
二、填空题(本大题共5小题,满分20分,只要求填写最后结果,每小题填对得4分)
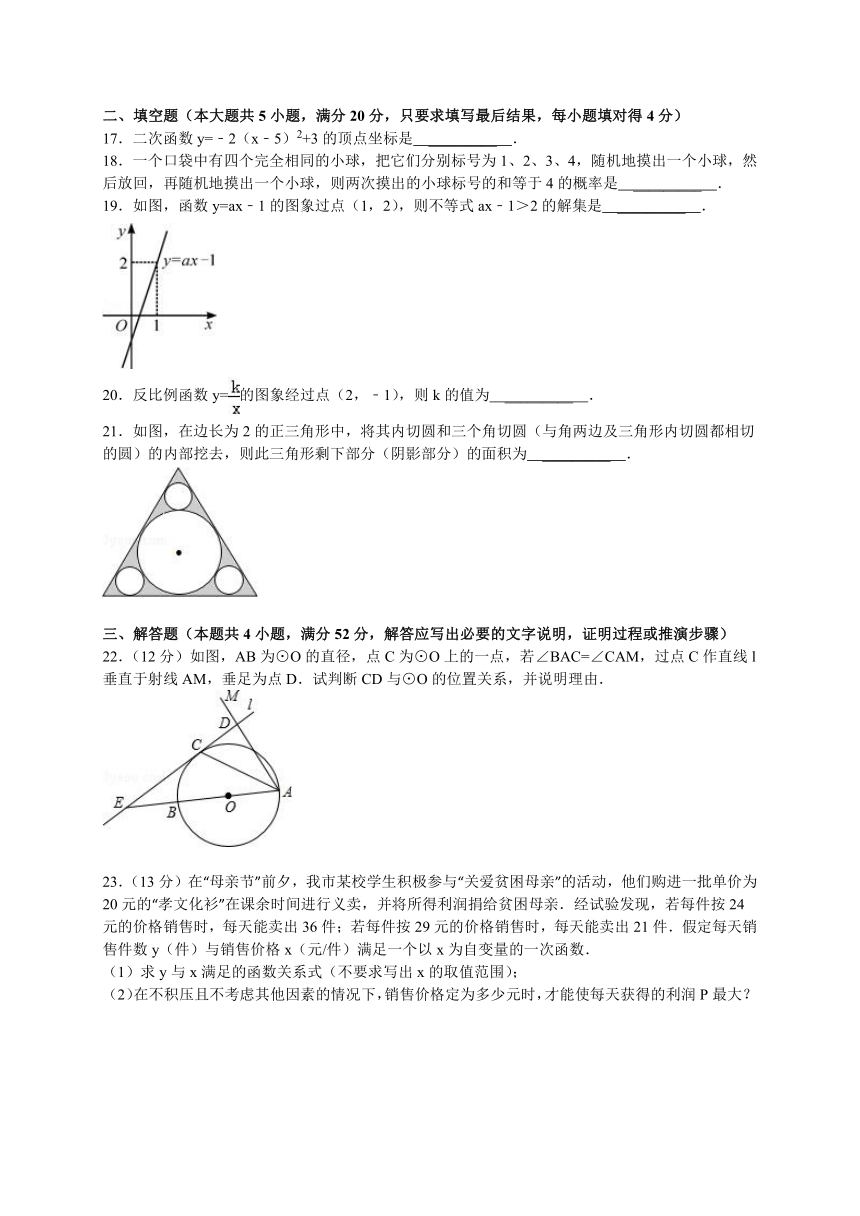
17.二次函数y=﹣2(x﹣5)2+3的顶点坐标是 _________ .
18.一个口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸出一个小球,然后放回,再随机地摸出一个小球,则两次摸出的小球标号的和等于4的概率是 _________ .
19.如图,函数y=ax﹣1的图象过点(1,2),则不等式ax﹣1>2的解集是 _________ .
20.反比例函数y=的图象经过点(2,﹣1),则k的值为 _________ .
21.如图,在边长为2的正三角形中,将其内切圆和三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则此三角形剩下部分(阴影部分)的面积为 _________ .
三、解答题(本题共4小题,满分52分,解答应写出必要的文字说明,证明过程或推演步骤)
22.(12分)如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由.
23.(13分)在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试验发现,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
24.(13分)工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
25.(14分)如图,已知抛物线y=﹣x2+bx+4与x轴相交于AB两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).(1)求抛物线的表达式及它的对称轴方程;
(2)求点C的坐标,并求线段BC所在直线的函数表达式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
一、选择题(本大题共16小题,每小题3分,共48分)
1.已知⊙O1与⊙O2相切,⊙O1的半径为3cm,⊙O2的半径为2cm,则O1O2的长是( )
A. 1cm B. 5cm C. 1cm或5cm D. 0.5cm或2.5cm
2.如图,点A,B,C在⊙O上,∠A=50°,则∠BOC的度数为( )
A. 40° B. 50° C. 80° D. 100°
3.二次函数y=ax2+bx+c图象上部分点的坐标满足下表:
x … ﹣3 ﹣2 ﹣1 0 1 …
y … ﹣3 ﹣2 ﹣3 ﹣6 ﹣11 …
则该函数图象的顶点坐标为( )
A. (﹣3,﹣3) B. (﹣2,﹣2) C. (﹣1,﹣3) D. (0,﹣6)
4. 2013年“五 一”期间,小明与小亮两家准备从东营港、黄河入海口、龙悦湖中选择一景点游玩,小明与小亮通过抽签方式确定景点,则两家抽到同一景点的概率是( )
A. B. C. D.
5.将二次函数y=x2的图象向右平移一个单位长度,再向上平移3个单位长度所得的图象解析式为( )
A. y=(x﹣1)2+3 B. y=(x+1)2+3 C. y=(x﹣1)2﹣3 D. y=(x+1)2﹣3
6.反比例函数y=的图象如图所示,以下结论:
①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
7.若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )
8.已知二次函数y=x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣3x+m=0的两实数根是( )
A. x1=1,x2=﹣1 B. x1=1,x2=2 C. x1=1,x2=0 D. x1=1,x2=3
9.若二次函数y=ax2的图象经过点P(﹣2,4),则该图象必经过点( )
A. (2,4) B. (﹣2,﹣4) C. (﹣4,2) D. (4,﹣2)
10.如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2.则S阴影=( )
A. π B. 2π C. D. π
11.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
12.如图,函数y=﹣x与函数y=﹣的图象相交于A、B两点,过AB两点分别作y轴的垂线,垂足分别为C、D,则四边形ABCD的面积为( )
A. 2 B. 4 C. 6 D. 8
13.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.
其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
14.绍兴是著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )
A. 4m B. 5m C. 6m D. 8m
15.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A. 30° B. 45° C. 60° D. 90°
16.如图,直线y=与双曲线y=(k>0,x>0)交于点A,将直线y=向上平移4个单位长度后,与y轴交于点C,与双曲线y=(k>0,x>0)交于点B,若OA=3BC,则k的值为( )
A. 3 B. 6 C. D.
二、填空题(本大题共5小题,满分20分,只要求填写最后结果,每小题填对得4分)
17.二次函数y=﹣2(x﹣5)2+3的顶点坐标是 _________ .
18.一个口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸出一个小球,然后放回,再随机地摸出一个小球,则两次摸出的小球标号的和等于4的概率是 _________ .
19.如图,函数y=ax﹣1的图象过点(1,2),则不等式ax﹣1>2的解集是 _________ .
20.反比例函数y=的图象经过点(2,﹣1),则k的值为 _________ .
21.如图,在边长为2的正三角形中,将其内切圆和三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则此三角形剩下部分(阴影部分)的面积为 _________ .
三、解答题(本题共4小题,满分52分,解答应写出必要的文字说明,证明过程或推演步骤)
22.(12分)如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由.
23.(13分)在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试验发现,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
24.(13分)工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
25.(14分)如图,已知抛物线y=﹣x2+bx+4与x轴相交于AB两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).(1)求抛物线的表达式及它的对称轴方程;
(2)求点C的坐标,并求线段BC所在直线的函数表达式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
同课章节目录
