北师大版六年级数学下册1.面的旋转同步练习(含答案)
文档属性
| 名称 | 北师大版六年级数学下册1.面的旋转同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 102.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 00:00:00 | ||
图片预览


文档简介
1.面的旋转 同步练习 六年级数学下册(北师大版)含答案
一、填空题
1.下图中每个小方格的边长是1分米,当( )分米时。剪下图中的阴影部分恰好可以围成一个圆柱(接头处忽略不计)。
2.把一个长方形绕着它的一条边旋转一周会形成一个( )。把这个长方形水平放置并向上平移10厘米则会形成一个( )。
3.将一个长是5cm,宽是4cm的长方形绕它的一条边所在的直线为轴旋转成一个圆柱,这个圆柱的底面周长可能是( )cm,也可能是( )cm。
4.将一条线段的一个端点不动,另一个端点旋转一周,其轨迹所形成的图形是( );将一个半圆形沿着它的直径旋转一周,其轨迹所形成的图形是( )。
二、选择题
5.用丝带捆扎一种圆柱形礼品盒,打结处为20厘米。捆扎这种礼品盒用长为( )厘米的丝带比较合适。
A.22分米 B.240厘米 C.19.5分米 D.22.5分米
6.制作一个无盖的水桶,以下哪种铁皮可供搭配?应选择( )。
A.①和④ B.②和③ C.①和③
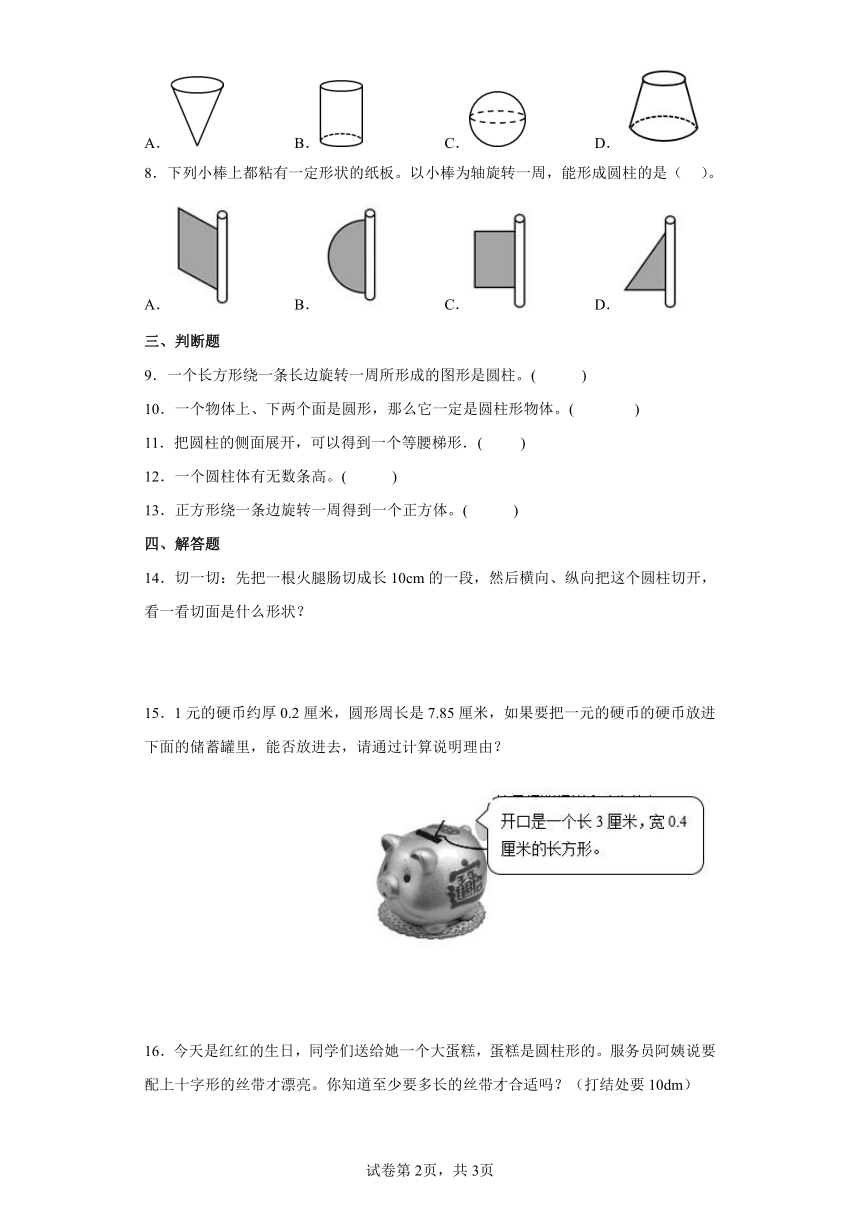
7.观察下面的图形,( )是圆柱。
A. B. C. D.
8.下列小棒上都粘有一定形状的纸板。以小棒为轴旋转一周,能形成圆柱的是( )。
A. B. C. D.
三、判断题
9.一个长方形绕一条长边旋转一周所形成的图形是圆柱。( )
10.一个物体上、下两个面是圆形,那么它一定是圆柱形物体。( )
11.把圆柱的侧面展开,可以得到一个等腰梯形.( )
12.一个圆柱体有无数条高。( )
13.正方形绕一条边旋转一周得到一个正方体。( )
四、解答题
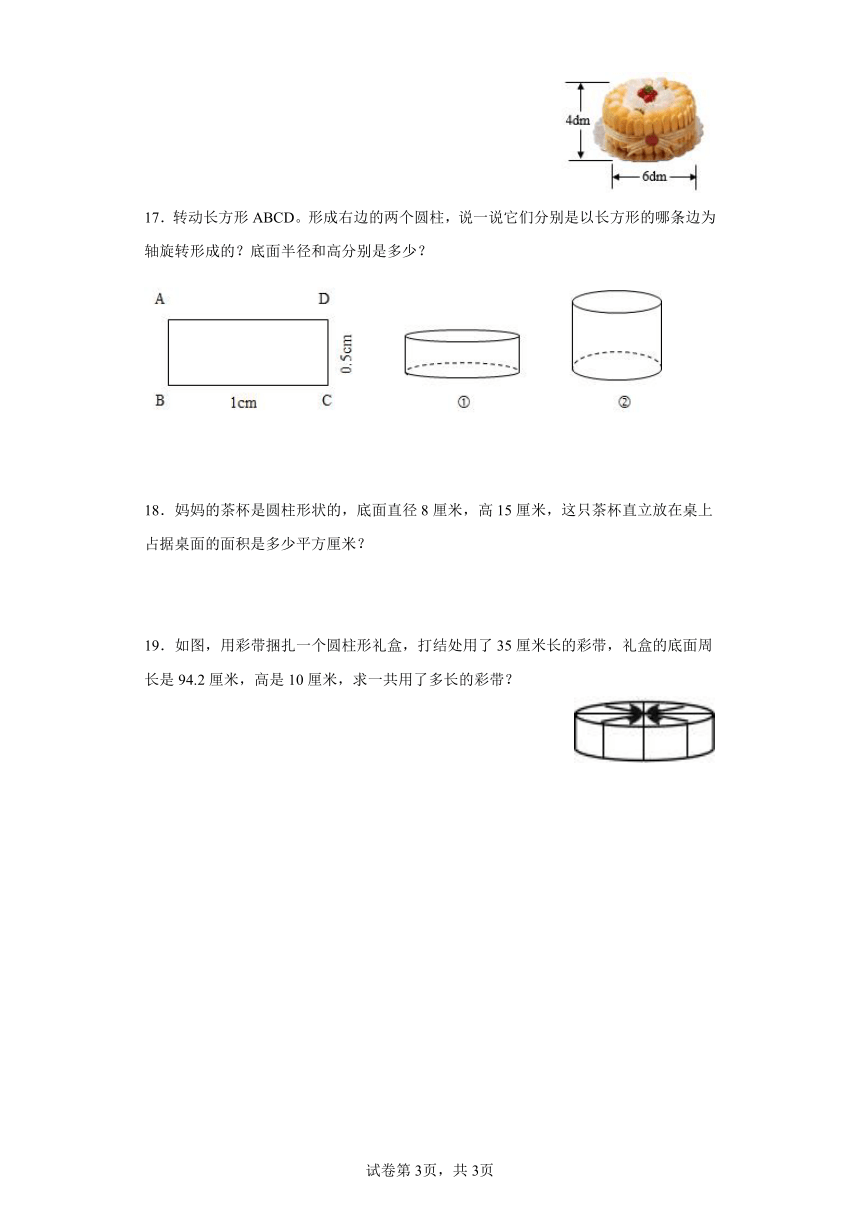
14.切一切:先把一根火腿肠切成长10cm的一段,然后横向、纵向把这个圆柱切开,看一看切面是什么形状?
15.1元的硬币约厚0.2厘米,圆形周长是7.85厘米,如果要把一元的硬币的硬币放进下面的储蓄罐里,能否放进去,请通过计算说明理由?
16.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的。服务员阿姨说要配上十字形的丝带才漂亮。你知道至少要多长的丝带才合适吗?(打结处要10dm)
17.转动长方形ABCD。形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
18.妈妈的茶杯是圆柱形状的,底面直径8厘米,高15厘米,这只茶杯直立放在桌上占据桌面的面积是多少平方厘米?
19.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.6.28
【分析】由图可知,圆的半径是1分米,要使阴影部分恰好可以围成一个圆柱,则长方形的底边长等于圆的周长,根据圆的周长公式:周长=2×π×半径,代入数据,即可解答。
【详解】x=2×3.14×1
=6.28×1
=6.28(分米)
2.圆柱 长方体
【分析】根据圆柱的定义,把一个长方形绕着它的一条边旋转一周会形成一个圆柱。把这个长方形水平放置并向上平移10厘米,平移的过程中会产生四个侧面,而原来的长方形和平移后的长方形分别是上、下面,即形成一个长方体。
【详解】把一个长方形绕着它的一条边旋转一周会形成一个圆柱。把这个长方形水平放置并向上平移10厘米则会形成一个长方体。
3. 25.12 31.4
【分析】绕长边所在的直线为轴旋转成一个底面半径为4厘米的圆柱;绕宽边所在的直线为轴旋转成一个底面半径为5厘米的圆柱;将数据分别代入圆的周长公式计算即可。
【详解】3.14×4×2
=3.14×8
=25.12(cm)
3.14×5×2
=3.14×10
=31.4(cm)
4. 圆 球体
【详解】圆的定义:当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹就是一个圆;球是以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体,也叫做球体。
5.B
【分析】通过观察,捆扎这个盒子至少用去丝带长度为4个礼品盒底面直径和4个礼品盒高,再加上打结用去绳长的20厘米,由此得解。
【详解】30×4+25×4+20
=120+100+20
=240(厘米)
捆扎这种礼品盒用长为240厘米的丝带比较合适。
故答案为:B
6.B
【分析】根据圆的周长公式:周长=π×半径×2,代入数据,求出直径是3cm和半径是4cm的圆的周长,再进行比较,圆的周长与长方形的长相等,即可搭配成圆柱形水桶,据此解答。
【详解】直径3cm圆的周长:
3.14×3=9.42(cm)
半径4cm的圆的周长:
3.14×4×2
=12.56×2
=25.12(cm)
9.42=9.42
②和③可以搭配。
故答案为:B
7.B
【分析】根据圆柱的特征,圆柱的上、下面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的对面周长,长方形的宽等于圆柱的高;据此判断即可。
【详解】根据分析可知:
A.是圆锥;
B.是圆柱;
C.是一球体;
D.是圆台。
故答案为:B
8.C
【分析】根据各平面图形的特征,长方形或正方形绕一边旋转一周得到一个圆柱,由此解答即可。
【详解】长方形或正方形绕一边旋转一周得到一个圆柱。
故答案为:C
9.√
【分析】根据圆柱的意义,以长方形的一边为旋转轴,其余三边旋转形成的面围成的旋转体叫做圆柱,所以一个长方形绕着长为轴旋转一周,可以得到一个圆柱体,据此解答即可。
【详解】圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。由此可知:一个长方形绕它的一条长旋转一周后得到的图形是圆柱。
故判断正确。
10.×
【分析】根据圆柱的特征进行判断即可。
【详解】圆柱的每一个横截面都是相等的,且圆柱的侧面展开是一个长方形,一个物体上、下两个面是圆形,它不一定是圆柱体,如我们生活中认识的腰鼓,上下的是圆形,但它不是圆柱体,所以,一个物体上、下两个面是圆形,那么它一定是圆柱体说法数错误的。
故答案为:×
11.错误
【详解】因为把一个圆柱沿高剪开,当圆柱的底面周长等于圆柱的高时,展开的图形是正方形;
当圆柱的底面周长不等于圆柱的高时,展开的图形是长方形;
当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形,
所以,将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形;
无论如何将圆柱的侧面展开都不会得到一个等腰梯形.
故答案为错误.
【分析】因为圆柱是由上下两个完全一样的圆面和一个侧面组成的图形,因此无论如何将圆柱的侧面展开都不会得到一个等腰梯形.
12.√
【分析】根据圆柱的高的概念圆柱两个底面之间的距离叫做圆柱的高,判断即可。
【详解】一个圆柱体有无数条高。
故答案为:√
13.×
【分析】根据圆柱体的特征,圆柱体的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面展开是一个长方形;由此得出沿着它的一条边轴旋转一周得到的立体图形是一个圆柱。
【详解】沿着长方形的一条边轴旋转一周得到的立体图形是一个圆柱。
故答案为:×
14.圆,长方形(或正方形)。
【详解】横向切开是平行于底面切开的,切开后切面是圆形;纵向切开是平行于高切开的,切开后切面是长方形(或正方形).
15.能;见详解
【分析】根据圆的周长公式,求出圆的直径,用直径与开口的长、厚度与开口的宽比较即可。
【详解】(厘米)
2.5<3
0.2<0.4
答:能放进去。
16.50分米
【分析】由图可知,捆扎这个盒子至少用去4个底面直径和4个高长度的和,再加上打结用去丝带的长度10分米,据此解答。
【详解】6×4+4×4+10
=24+16+10
=40+10
=50(分米)
答:至少要50分米的丝带才合适。
17.【分析】根据面动成体,转动长方形ABCD,以AB或CD边为轴旋转一周,得到的圆柱高为0.5cm,底面半径为1cm,生成圆柱①;以AD或BC为轴旋转一周得到的圆柱高为1cm,底面半径为0.5cm,生成圆柱②。
【详解】答:圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1cm,圆柱高为0.5cm;
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5cm,圆柱高为1cm。
18.50.24平方厘米
【分析】根据题目可知,这个茶杯是圆柱形,茶杯直立放在桌面上占据桌面的面积就是圆柱的底面圆的面积,根据圆的面积公式:S=πr2,把数代入即可。
【详解】3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
答:这只茶杯直立放在桌面上占据桌面的面积是50.24平方厘米。
19.355厘米
【分析】根据题意可知,先求出这个圆柱的底面直径,观察图可知,彩带的长度=底面直径的长度×8+圆柱的高×8+打结部分的长度,据此列式解答。
【详解】94.2÷3.14×8+10×8+35
=240+80+35
=355(厘米)
答:一共用了355厘米的彩带。
答案第1页,共2页
答案第1页,共2页
一、填空题
1.下图中每个小方格的边长是1分米,当( )分米时。剪下图中的阴影部分恰好可以围成一个圆柱(接头处忽略不计)。
2.把一个长方形绕着它的一条边旋转一周会形成一个( )。把这个长方形水平放置并向上平移10厘米则会形成一个( )。
3.将一个长是5cm,宽是4cm的长方形绕它的一条边所在的直线为轴旋转成一个圆柱,这个圆柱的底面周长可能是( )cm,也可能是( )cm。
4.将一条线段的一个端点不动,另一个端点旋转一周,其轨迹所形成的图形是( );将一个半圆形沿着它的直径旋转一周,其轨迹所形成的图形是( )。
二、选择题
5.用丝带捆扎一种圆柱形礼品盒,打结处为20厘米。捆扎这种礼品盒用长为( )厘米的丝带比较合适。
A.22分米 B.240厘米 C.19.5分米 D.22.5分米
6.制作一个无盖的水桶,以下哪种铁皮可供搭配?应选择( )。
A.①和④ B.②和③ C.①和③
7.观察下面的图形,( )是圆柱。
A. B. C. D.
8.下列小棒上都粘有一定形状的纸板。以小棒为轴旋转一周,能形成圆柱的是( )。
A. B. C. D.
三、判断题
9.一个长方形绕一条长边旋转一周所形成的图形是圆柱。( )
10.一个物体上、下两个面是圆形,那么它一定是圆柱形物体。( )
11.把圆柱的侧面展开,可以得到一个等腰梯形.( )
12.一个圆柱体有无数条高。( )
13.正方形绕一条边旋转一周得到一个正方体。( )
四、解答题
14.切一切:先把一根火腿肠切成长10cm的一段,然后横向、纵向把这个圆柱切开,看一看切面是什么形状?
15.1元的硬币约厚0.2厘米,圆形周长是7.85厘米,如果要把一元的硬币的硬币放进下面的储蓄罐里,能否放进去,请通过计算说明理由?
16.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的。服务员阿姨说要配上十字形的丝带才漂亮。你知道至少要多长的丝带才合适吗?(打结处要10dm)
17.转动长方形ABCD。形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
18.妈妈的茶杯是圆柱形状的,底面直径8厘米,高15厘米,这只茶杯直立放在桌上占据桌面的面积是多少平方厘米?
19.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.6.28
【分析】由图可知,圆的半径是1分米,要使阴影部分恰好可以围成一个圆柱,则长方形的底边长等于圆的周长,根据圆的周长公式:周长=2×π×半径,代入数据,即可解答。
【详解】x=2×3.14×1
=6.28×1
=6.28(分米)
2.圆柱 长方体
【分析】根据圆柱的定义,把一个长方形绕着它的一条边旋转一周会形成一个圆柱。把这个长方形水平放置并向上平移10厘米,平移的过程中会产生四个侧面,而原来的长方形和平移后的长方形分别是上、下面,即形成一个长方体。
【详解】把一个长方形绕着它的一条边旋转一周会形成一个圆柱。把这个长方形水平放置并向上平移10厘米则会形成一个长方体。
3. 25.12 31.4
【分析】绕长边所在的直线为轴旋转成一个底面半径为4厘米的圆柱;绕宽边所在的直线为轴旋转成一个底面半径为5厘米的圆柱;将数据分别代入圆的周长公式计算即可。
【详解】3.14×4×2
=3.14×8
=25.12(cm)
3.14×5×2
=3.14×10
=31.4(cm)
4. 圆 球体
【详解】圆的定义:当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹就是一个圆;球是以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体,也叫做球体。
5.B
【分析】通过观察,捆扎这个盒子至少用去丝带长度为4个礼品盒底面直径和4个礼品盒高,再加上打结用去绳长的20厘米,由此得解。
【详解】30×4+25×4+20
=120+100+20
=240(厘米)
捆扎这种礼品盒用长为240厘米的丝带比较合适。
故答案为:B
6.B
【分析】根据圆的周长公式:周长=π×半径×2,代入数据,求出直径是3cm和半径是4cm的圆的周长,再进行比较,圆的周长与长方形的长相等,即可搭配成圆柱形水桶,据此解答。
【详解】直径3cm圆的周长:
3.14×3=9.42(cm)
半径4cm的圆的周长:
3.14×4×2
=12.56×2
=25.12(cm)
9.42=9.42
②和③可以搭配。
故答案为:B
7.B
【分析】根据圆柱的特征,圆柱的上、下面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的对面周长,长方形的宽等于圆柱的高;据此判断即可。
【详解】根据分析可知:
A.是圆锥;
B.是圆柱;
C.是一球体;
D.是圆台。
故答案为:B
8.C
【分析】根据各平面图形的特征,长方形或正方形绕一边旋转一周得到一个圆柱,由此解答即可。
【详解】长方形或正方形绕一边旋转一周得到一个圆柱。
故答案为:C
9.√
【分析】根据圆柱的意义,以长方形的一边为旋转轴,其余三边旋转形成的面围成的旋转体叫做圆柱,所以一个长方形绕着长为轴旋转一周,可以得到一个圆柱体,据此解答即可。
【详解】圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。由此可知:一个长方形绕它的一条长旋转一周后得到的图形是圆柱。
故判断正确。
10.×
【分析】根据圆柱的特征进行判断即可。
【详解】圆柱的每一个横截面都是相等的,且圆柱的侧面展开是一个长方形,一个物体上、下两个面是圆形,它不一定是圆柱体,如我们生活中认识的腰鼓,上下的是圆形,但它不是圆柱体,所以,一个物体上、下两个面是圆形,那么它一定是圆柱体说法数错误的。
故答案为:×
11.错误
【详解】因为把一个圆柱沿高剪开,当圆柱的底面周长等于圆柱的高时,展开的图形是正方形;
当圆柱的底面周长不等于圆柱的高时,展开的图形是长方形;
当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形,
所以,将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形;
无论如何将圆柱的侧面展开都不会得到一个等腰梯形.
故答案为错误.
【分析】因为圆柱是由上下两个完全一样的圆面和一个侧面组成的图形,因此无论如何将圆柱的侧面展开都不会得到一个等腰梯形.
12.√
【分析】根据圆柱的高的概念圆柱两个底面之间的距离叫做圆柱的高,判断即可。
【详解】一个圆柱体有无数条高。
故答案为:√
13.×
【分析】根据圆柱体的特征,圆柱体的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面展开是一个长方形;由此得出沿着它的一条边轴旋转一周得到的立体图形是一个圆柱。
【详解】沿着长方形的一条边轴旋转一周得到的立体图形是一个圆柱。
故答案为:×
14.圆,长方形(或正方形)。
【详解】横向切开是平行于底面切开的,切开后切面是圆形;纵向切开是平行于高切开的,切开后切面是长方形(或正方形).
15.能;见详解
【分析】根据圆的周长公式,求出圆的直径,用直径与开口的长、厚度与开口的宽比较即可。
【详解】(厘米)
2.5<3
0.2<0.4
答:能放进去。
16.50分米
【分析】由图可知,捆扎这个盒子至少用去4个底面直径和4个高长度的和,再加上打结用去丝带的长度10分米,据此解答。
【详解】6×4+4×4+10
=24+16+10
=40+10
=50(分米)
答:至少要50分米的丝带才合适。
17.【分析】根据面动成体,转动长方形ABCD,以AB或CD边为轴旋转一周,得到的圆柱高为0.5cm,底面半径为1cm,生成圆柱①;以AD或BC为轴旋转一周得到的圆柱高为1cm,底面半径为0.5cm,生成圆柱②。
【详解】答:圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1cm,圆柱高为0.5cm;
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5cm,圆柱高为1cm。
18.50.24平方厘米
【分析】根据题目可知,这个茶杯是圆柱形,茶杯直立放在桌面上占据桌面的面积就是圆柱的底面圆的面积,根据圆的面积公式:S=πr2,把数代入即可。
【详解】3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
答:这只茶杯直立放在桌面上占据桌面的面积是50.24平方厘米。
19.355厘米
【分析】根据题意可知,先求出这个圆柱的底面直径,观察图可知,彩带的长度=底面直径的长度×8+圆柱的高×8+打结部分的长度,据此列式解答。
【详解】94.2÷3.14×8+10×8+35
=240+80+35
=355(厘米)
答:一共用了355厘米的彩带。
答案第1页,共2页
答案第1页,共2页
