北师大版六年级数学下册1.圆柱的表面积同步练习(含答案)
文档属性
| 名称 | 北师大版六年级数学下册1.圆柱的表面积同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 230.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 00:00:00 | ||
图片预览

文档简介
1.圆柱的表面积 同步练习
六年级数学下册(北师大版)含答案
一、填空题
1.(如图)将圆柱形纸筒沿虚线剪开得到一个长方形,这个长方形的长是( )厘米,宽是( )厘米。(π取3.14)
(第1题) (第2题)
2.如图,是一个圆柱的侧面展开图,这个圆柱的表面积是( )。
3.一个无盖的圆柱形铁皮水桶,底面直径是20厘米,高是50厘米。做这样一个水桶,至少需要( )平方厘米铁皮。
4.一个圆柱,它的底面直径是6cm,比高多,这个圆柱的表面积是( )cm2。
5.一个圆柱的底面直径是4cm、高是18cm,这个圆柱的表面积是( )平方厘米。
6.把边长是8分米的正方形纸围成一个圆柱形纸筒(接头处不计),这个纸筒的侧面积是( )平方分米。
7.一种固体胶棒,它的底面周长是3.14厘米,高是6厘米,只包装它的侧面,包装一个需要( )平方厘米的包装纸。如果有1平方米的包装纸,最多能包装( )个固体胶棒。
8.一个圆柱的高增加2厘米,底面半径不变,表面积就增加了12.56平方厘米,则这个圆柱的底面周长是( )厘米。
9.一个底面周长为4cm的圆柱体侧面展开后是一个正方形,这个圆柱体的高是( )cm,这个正方形的面积是( )cm2。
二、选择题
10.一个圆柱体的侧面展开图是正方形,这个圆柱体的底面直径与高的比是( )。
A.2π∶1 B.1∶1 C.1∶π D.π∶1
11.将一个圆柱的侧面展开,一定得不到( )。
A.长方形 B.正方形 C.梯形
12.制作一个无盖的圆柱形水桶,有下图中几种型号的铁皮可供选择,一共可以搭配出( )种不同容积的水桶。
A.2 B.3 C.4 D.1
13.下面各图形中,( )是圆柱的展开图。(单位:cm)
A. B.
C. D.
14.一个圆柱,底面直径和高都是2分米,这个圆柱的侧面积是( )平方分米。
A.6π B.5π C.4π D.2π
15.一个圆柱形木棒,高是8分米,如果从上面将它的高截短,那么表面积比原来减少6.28平方分米,原来这根木棒的表面积是( )平方分米。
A.15.7 B.18.84 C.25.12 D.26.69
16.把一个棱长2分米的正方体削成一个最大的圆柱,这个圆柱的侧面积是( )。
A.18.84平方分米 B.6.28平方分米 C.3.14平方分米 D.12.56平方分米
17.一个圆柱的侧面展开图是一个正方形。这个圆柱的高是底面直径的( )倍。
A. B.2 C. D.
18.圆柱的侧面积的大小是由( )决定的。
A.底面半径 B.圆柱的高 C.底面半径和圆柱的高
19.用铁皮制作一个有盖的圆柱形油桶,底面半径是3分米,高与底面半径的比是2∶1。制作这个油桶至少需要( )平方分米的铁皮。
A.56.52 B.75.36 C.113.04 D.169.56
20.一个圆柱的底面周长是18.84米,高是2米,则这个圆柱的表面积是( )平方米。
A.94.2 B.65.94 C.56.52 D.37.68
21.(如图)同一个圆柱切分后,表面积比原来增加4rh的图是( )。
A.甲
B.乙
C.两个都是
D.两个都不是
三、判断题
22.一个圆柱的侧面沿高展开后恰好是一个正方形,圆柱的底面半径是2分米,圆柱的高是12.56分米。( )
23.,左图是一个圆柱的展开图。( )
24.圆柱的侧面展开可能是长方形,也可能是正方形。( )
25.圆柱底面半径扩大到原来的2倍,高不变,那么它的侧面积也随着扩大到原来的2倍。( )
26.一个圆柱体的高增加4厘米,它的表面积就比原来增加12.56平方厘米,则这个圆柱体的底面半径是1厘米。( )
27.一根长为1.5m的圆柱形木料,锯掉4dm长的一段后,表面积比原来减少了50.24dm2,这根木料原来的底面半径是2dm。( )
28.把一个圆柱平均切成3个小圆柱,那么每个小圆柱的表面积是原圆柱表面积的。( )
29.圆柱的底面半径扩大到原来的3倍,高不变,它的侧面积和底面积都扩大到原来的3倍。( )
四、图形计算
30.计算下图圆柱的表面积。
31.计算下面半个圆柱的表面积。
32.计算下面图形的表面积。
五、解答题
33.如图,用下面的长方形硬纸卷成圆柱形小笔筒,再给这个笔筒配一个底,想一想,还需要多少平方厘米的硬纸片?(请写出两种情况)
34.如图所示,明明和芳芳分别用纸剪下了两个相等的圆和一个长方形,想制作成圆柱。(单位:厘米)取
(1)他们两个剪下的图形都能围成圆柱吗?请在你认为可以围成圆柱的图下面画“√”。
(2)请计算围成的圆柱的表面积。
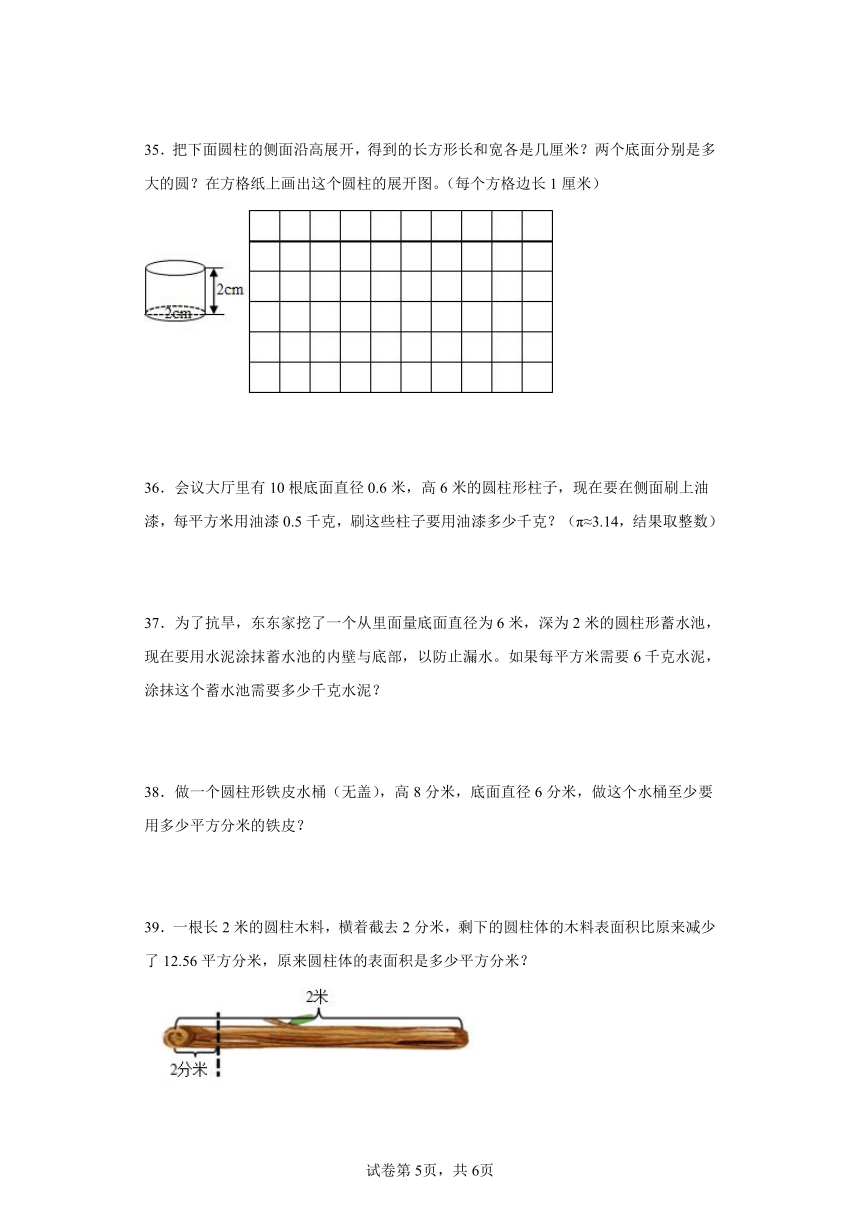
35.把下面圆柱的侧面沿高展开,得到的长方形长和宽各是几厘米?两个底面分别是多大的圆?在方格纸上画出这个圆柱的展开图。(每个方格边长1厘米)
36.会议大厅里有10根底面直径0.6米,高6米的圆柱形柱子,现在要在侧面刷上油漆,每平方米用油漆0.5千克,刷这些柱子要用油漆多少千克?(π≈3.14,结果取整数)
37.为了抗旱,东东家挖了一个从里面量底面直径为6米,深为2米的圆柱形蓄水池,现在要用水泥涂抹蓄水池的内壁与底部,以防止漏水。如果每平方米需要6千克水泥,涂抹这个蓄水池需要多少千克水泥?
38.做一个圆柱形铁皮水桶(无盖),高8分米,底面直径6分米,做这个水桶至少要用多少平方分米的铁皮?
39.一根长2米的圆柱木料,横着截去2分米,剩下的圆柱体的木料表面积比原来减少了12.56平方分米,原来圆柱体的表面积是多少平方分米?
40.妈妈给笑笑的水杯做了一个带底的敞口布套,如图所示。妈妈至少用了多少平方厘米布料?(接头处忽略不计)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1. 21.98 4
【分析】由图可知:圆柱的底面直径是7厘米,高是4厘米,将圆柱形纸筒沿虚线剪开得到一个长方形,根据圆柱侧面展开图的特征,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,根据圆的周长公式C=πd,代入数据解答即可。
【详解】由分析可知:
长方形的长:3.14×7=21.98(厘米)
长方形的宽=圆柱的高=4厘米
2.87.92
【分析】观察图形可知,圆柱的底面周长是12.56cm,高是5cm;根据圆的周长公式:周长=π×2×半径;半径=周长÷2÷π;代入数据,求出圆柱的底面半径;再根据圆柱的表面积公式:底面积×2+侧面积;代入数据,即可解答。
【详解】半径:12.56÷2÷3.14
=6.28÷3.14
=2(cm)
表面积:3.14×22×2+12.56×5
=3.14×4×2+62.8
=12.56×2+62.8
=25.12+62.8
=87.92(cm2)
3.3454
【分析】据题分析,做该水桶需要的铁皮,即是求该圆柱的表面积,圆柱的表面积为圆柱侧面积加上两个底面积,因为是无盖,没有上底面积,只需要用圆柱侧面积加上一个下底面积即可。根据圆柱侧面积公式,S=Ch,再根据圆的面积公式:S=r2,代入数值求解即可。
【详解】圆柱侧面积为:
20×3.14×50
=62.8×50
=3140(平方厘米)
底面积为:
3.14×(20÷2)2
=3.14×102
=3.14×100
=314(平方厘米)
共需要铁皮数:
3140+314=3454(平方厘米)
4.131.88
【分析】据题意可以求出圆柱的高是多少,再根据圆柱的表面积的公式=两个底面积+侧面积,可以求出圆柱的表面积是多少,列式解答即可。
【详解】6÷(1+)
=6×
=4(cm)
3.14×6×4+3.14×(6÷2)2×2
=3.14×24+3.14×18
=3.14×42
=131.88(cm2)
5.251.2
【分析】根据圆柱的表面积公式:表面积=侧面积+底面积×2,代入数据,即可解答。
【详解】3.14×4×18+3.14×(4÷2)2×2
=12.56×18+3.14×4×2
=226.08+12.56×2
=226.08+25.12
=251.2(平方厘米)
6.64
【分析】根据题意,因为接头处不计,所以围成纸筒的侧面积就等于这个正方形纸的面积,根据正方形的面积公式S=a×a,计算即可得到答案。
【详解】根据分析可知:
8×8=64(平方分米)
7. 18.84 530
【分析】根据圆柱的侧面积公式:S=ch,把数据代入公式解答,把1平方米换成10000平方厘米,看看10000平方厘米的里面有多少个18.84即可。
【详解】3.14×6=18.84(平方厘米)
1平方米=10000平方厘米
10000÷18.84=530(个)……14.8(平方厘米)
所以最多能包装530个固体胶棒。
8.6.28
【分析】根据题意可知,把圆柱的高增加2厘米,底面半径不变,表面积就增加了12.56平方厘米,表面积增加的是高为2厘米的圆柱的侧面积,根据圆柱的侧面积公式:S=Ch,那么C=S÷h,把数据代入公式解答。
【详解】12.56÷2=6.28(厘米),这个圆柱的底面周长是6.28厘米。
9. 4 16
【分析】圆柱的侧面展开后是正方形,说明圆柱的底面周长等于高。底面周长为4cm,则这个圆柱的高也是4cm。展开后的正方形的面积就是圆柱的侧面积,圆柱的侧面积=底面周长×高,据此代入数据计算。
【详解】一个底面周长为4cm的圆柱体侧面展开后是一个正方形,这个圆柱体的高是4cm;4×4=16(cm2),这个正方形的面积是16cm2。
10.C
【分析】一个圆柱体的侧面展开图是正方形,说明圆柱的底面周长与高相等,据此解答。
【详解】假设圆的底面直径为d,则圆柱的高为πd,
d∶πd=1∶π
故答案为:C
11.C
【分析】根据圆柱的侧面展开图的特点,将圆柱侧面的几种展开图方法与选项进行对比,即可进行选择。
【详解】圆柱的侧面沿高展开可能是长方形或正方形,如果斜着展开是一个平行四边形,因为圆柱的上下底面是完全相同的两个圆,所以圆柱的侧面展开图不可能是梯形。
故答案为:C
12.A
【分析】制作无盖的圆柱形水桶,说明要选一个长方形和一个圆形铁皮,而且所选的长方形的一条边和圆的周长相等即可达到要求;根据圆的周长公式:周长=π×直径,求出圆的周长,与长方形的长进行比较,即可解答。
【详解】③周长:3.14×4=12.56(dm)
④周长:3.14×3×2
=9.42×2
=18.84(dm)
⑤周长:3.14×3=9.42(dm)
①和⑤搭配;②和③搭配;
共2组。
故答案为:A
13.C
【分析】圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长等于圆柱底面的周长,依据圆的周长公式将数值代人计算并选择。
【详解】A.2×3.14=628(cm),6.28≠9.42,所以不是圆柱的展开图;
B.4×3.14=12.56(cm),12.56≠9.42,所以不是圆柱的展开图;
C.3×3.14=9.42(cm),9.42=9.42,所以是圆柱的展开图;
D.4×3.14=12.56(cm),12.56≠9.42所以不是圆柱的展开图。
故答案为:C
14.C
【分析】圆柱侧面积=,代数解答即可。
【详解】
这个圆柱的侧面积是平方分米。
故答案为:C
15.D
【分析】根据题意可知,一个圆柱形木棒,高是8分米,从上面将它的高截短,也就是把高截短8×=2(分米),表面积减少6.28平方分米,表面积减少的是高2分米的圆柱的侧面积,根据圆柱的侧面积=底面周长×高,据此可以求出底面周长,从而求出底面半径,再根据圆柱的表面积=侧面积+底面积×2,把数据代入公式解答。
【详解】底面周长:
6.28÷(8×)
=6.28÷2
=3.14(分米)
底面半径:3.14÷3.14÷2=0.5(分米)
原来这根木棒的表面积:
3.14×8+3.14×0.52×2
=25.12+3.14×0.25×2
=25.12+1.57
=26.69(平方分米)
故答案为:D
16.D
【分析】根据题意,棱长是2分米的正方体木块,削成一个最大的圆柱,则它的直径为2分米,高也为2分米,根据圆柱的侧面积公式S=Ch,计算即可解答。
【详解】3.14×2×2
=6.28×2
=12.56(平方分米)
故答案为:D
17.A
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的等于圆柱的底面周长,宽等于圆柱的高,如果圆柱的侧面展开图是一个正方形,那么这个圆柱的底面周长和高相等,根据圆的周长公式:,据此解答即可。
【详解】一个圆柱的侧面展开图是一个正方形。那么这个圆柱的底面周长和高相等,由圆周率的意义,=圆周率(),所以这个圆柱的高是底面直径的倍。
故答案为:A
18.C
【分析】圆柱的侧面积=底面周长×高,而底面周长=半径×2×圆周率,据此解答。
【详解】根据圆柱侧面积和圆的周长公式可知,圆柱的侧面积的大小是由底面半径和圆柱的高决定的。
故答案为:C
19.D
【分析】根据题意可知,高与底面半径的比是2∶1,即高是底面半径的2倍,用底面半径×2,求出高;求制作这个油桶至少需要的铁皮,就是求这个圆柱形油桶的表面积,根据圆柱的表面积公式:表面积=底面积×2+侧面积,代入数据,即可解答。
【详解】高:6×2=6(分米)
3.14×32×2+3.14×3×2×6
=3.14×9×2+9.42×2×6
=28.26×2+18.84×6
=56.52+113.04
=169.56(平方分米)
故答案为:D
20.A
【分析】圆柱的表面积=侧面积+底面积×2,而圆柱的侧面积=底面周长×高。已知圆柱的底面周长,先根据“圆的周长=2πr”求出圆柱的底面半径,再根据“圆的面积=πr2”可以求出圆柱的底面积。分别把数据代入公式求出侧面积和底面积,最后求出圆柱的表面积。
【详解】18.84÷3.14÷2=3(米)
18.84×2+3.14×33×2
=37.68+56.52
=94.2(平方米)
故答案为:A
21.B
【分析】观察图形可知,甲图增加的面积是2个半径为r的圆的面积,根据圆的面积公式:π×半径2,求出增加的面;乙图增加的面积是2个长是底面直径,宽是圆柱的高的长方形面积;根据长方形面积公式:长×宽;求出增加的面积,即可解答。
【详解】甲图增加的面积:
π×r2×2
=2πr2
乙图增加的面积:
r×2×h×2
=4rh
故答案为:B
22.√
【分析】由题意可知,圆柱的底面周长等于高,已知底面半径,求底面周长,即圆柱的高;根据圆的周长公式:C=2πr,代入数据解答即可作出判断。
【详解】2×3.14×2
=6.28×2
=12.56(分米)
故答案为:√
23.√
【分析】根据圆柱的表面组成和其侧面展开图的特点,对题中的图进行分析即可。
【详解】圆柱的表面由3部分组成:上下是两个大小相等的圆,沿圆柱的高展开,得到一个长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,如果不是沿着高剪开,是沿着一条斜线剪开,则是。
故答案为:√
24.√
【分析】圆柱的侧面展开图,如图、、,可能是长方形、正方形或平行四边形,据此分析。
【详解】圆柱的侧面沿高展开是长方形,当底面周长=高时,展开图是正方形,把圆柱侧面斜着剪开得到一个平行四边形,所以原题说法正确。
故答案为:√
25.√
【分析】圆柱的底面半径扩大到原来的2倍,则圆柱的底面周长也扩大到原来的2倍,圆柱的侧面积=底面周长×高,圆柱的高不变,则它的侧面积也扩大到原来的2倍,举例说明即可。
【详解】假设圆柱的底面半径为r,高为h,则扩大后的底面半径为2r。
=2
所以,圆柱的侧面积也扩大到原来的2倍。
故答案为:√
26.×
【分析】根据题意可知,增加部分就是高是4厘米的圆柱的侧面积;也就是一个长方形面积;长等于底面周长,宽等于4厘米;根据长方形面积公式:面积=长×宽;长=面积÷宽;代入数据,求出这个圆柱的底面周长;再根据圆的周长公式:周长=π×半径×2;半径=周长÷π÷2,代入数据,求出这个圆柱底面的半径,进行解答。
【详解】12.56÷4=3.14(厘米)
3.14÷3.14÷2
=1÷2
=0.5(厘米)
一个圆柱体的高增加4厘米,它的表面积就比原来增加12.56平方厘米,则这个圆柱体的底面半径是0.5厘米。
原题干说法错误。
故答案为:×
27.√
【分析】表面积减少部分是长为4分米的圆柱的侧面积,利用圆柱的侧面积=底面周长×高可以求得这个圆柱的底面周长,从而求得它的半径,据此解答即可。
【详解】圆柱的底面半径为:
50.24÷4÷3.14÷2
=12.56÷3.14÷2
=2(dm)
这根木料原来的底面半径是2dm。
故答案为:√
28.×
【分析】把一个圆柱平均切割成3个小圆柱,侧面积是原来圆柱侧面积的,但是底面积没变,据此分析。
【详解】圆柱表面积=底面积×2+侧面积,小圆柱表面积=底面积×2+侧面积×,小圆柱表面积不是原来圆柱表面积的。
故答案为:×
29.×
【分析】圆柱的底面半径扩大到原来的3倍,设原来的底面半径为r,高为h,它的底面积=πr2,侧面积=2πrh,底面半径扩大原来的3倍,它的底面积=π(3r)2=9πr2,侧面积=2×π(3r)×h,即可算出它们侧面积和底面积扩大几倍。
【详解】设底面半径为r,高为h
它的底面积=πr2,侧面积=2πrh;
半径扩大3倍,半径为3r,高是h
扩大后圆柱的底面积=π(3r)2=9πr2.,侧面积=2×π(3r)h=6πrh
9πr2÷πr2=9
底面积扩大到原来的9倍;
6πrh÷2πrh=3
它的侧面积扩大到原来的3倍;
原题说法错误。
故答案为:×
30.244.92dm2
【分析】根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,圆的面积公式:S=πr2,圆的周长公式:C=2πr,把数据代入公式解答。
【详解】3.14×(6÷2)2×2
=3.14×18
=56.52(dm2)
2×3.14×3×10
=18.84×10
=188.4(dm2)
56.52+188.4=244..92(dm2)
31.151.62dm2
【分析】由图可知:这个半圆柱的表面积包括一个长方形的面积,圆柱的侧面积的一半及上下两个半圆的面积之和就是一个底面积;根据圆柱的表面积公式:,其中,,,代入数据进行计算即可。
【详解】
32.1411.2cm2
【分析】根据图分析,该组合体表面积,由一个圆柱体表面积加一个长方体表面积,再减去二者重合的部分,为圆柱体的两个底面积,由此可得,该组合图形表面积即为一个长方体的表面积加上一个圆柱体的侧面积,据此解题即可。
【详解】长方体表面积为:
(20×15+15×8+20×8)×2
=(300+120+160)×2
=(420+160)×2
=(420+160)×2
=580×2
=1160(cm2)
圆柱侧积为:
3.14×10×8
=31.4×8
=251.2(cm2)
组合体表面积为:
1160+251.2=1411.2(cm2)
33.50.24平方厘米或12.56平方厘米
【分析】由题,长方形硬纸卷成圆柱形小笔筒有两种方法:以长为底面周长或者以宽为底面周长;根据圆的周长公式C=2πr,先分别求出两种情况下的底面半径r,再根据圆的面积公式S=π分别求出两种情况下的面积即可。
【详解】以长为底面周长时:
25.12÷3.14÷2
=8÷2
=4(厘米)
3.14×
=3.14×16
=50.24(平方厘米)
以宽为底面周长时:
12.56÷3.14÷2
=4÷2
=2(厘米)
3.14×
=3.14×4
=12.56(平方厘米)
答:还需要50.24平方厘米或12.56平方厘米的硬纸片。
34.(1)明明能,芳芳不能;图见详解
(2)51.81平方厘米
【分析】(1)根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。根据圆的周长公式分别求出直径是3厘米、直径是5厘米的两个圆的周长,分别和两个长方形的长进行比较,如果圆的周长等于长方形的长,说明能围成圆柱,否则就不能围成圆柱。据此判断即可。
(2)根据圆柱的表面积=侧面积+底面积×2,把数据代入公式解答。
【详解】(1)明明剪下的圆的周长:
(厘米)
9.42厘米厘米
芳芳剪下的圆的周长:
(厘米)
15.7厘米≠8厘米≠5厘米
所以明明剪下的图形可以围成一个圆柱。
(2)
(平方厘米)
答:这个圆柱的表面积是51.81平方厘米。
35.长6.28;宽2厘米;两个直径为2厘米的圆;画图见详解
【分析】应明确圆柱由三部分组成:圆柱的侧面、圆柱的上、下两个底面;由题意可知:该圆柱的底面直径是2厘米,高为2厘米,根据“圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高”可知:先根据圆的周长=πd求出圆柱侧面展开后的长,宽为圆柱的高;圆柱的上下两个底面是直径为2厘米的圆,画出即可。
【详解】长方形的长:3.14×2=6.28(厘米)
长方形的宽是:2厘米
两个底面是两个直径为2厘米的圆。
据此画图如下:
36.56.52千克
【分析】圆柱侧面积=,代数求出一根柱子的侧面积,然后乘10求出10根侧面积,最后乘每平方米所用油漆量即可解答。
【详解】3.14×0.6×6×10×0.5
=11.304×10×0.5
=56.52(千克)
答:刷这些柱子要用油漆56.52千克。
37.395.64千克
【分析】由题意,抹水泥的是圆柱侧面积和一个底面积,根据公式计算出面积,再乘6即可。
【详解】
(千克)
答:涂抹这个蓄水池需要395.64千克水泥。
38.178.98平方分米
【分析】首先分清制作没有盖的圆柱形铁皮水桶,需要计算几个面的面积:侧面面积与底面圆的面积,由圆柱体侧面积和圆的面积计算方法解答即可。
【详解】3.14×+3.14×6×8
=3.14×9+3.14×48
=3.14×57
=178.98(平方分米)
答:做这个水桶至少要用178.98平方分米的铁皮。
39.131.88平方分米
【分析】由题意知,截去的部分是一个高为2分米的圆柱体,并且表面积减少了12.56平方分米,其实减少的面积就是截去部分的侧面积,由此可求出圆柱体的底面周长,进一步可求出底面积是多少,利用表面积=底面积×2+底面周长×高,即可求出这个圆柱的表面积。
【详解】底面周长:12.56÷2=6.28(分米)
底面半径:6.28÷3.14÷2
=2÷2
=1(分米)
底面积:3.14×12
=3.14×1
=3.14(平方分米)
2米=20分米
表面积:6.28×20+3.14×2
=125.6+6.28
=131.88(平方分米)
答:原来圆柱体的表面积是131.88平方分米。
40.292.02平方厘米
【分析】求至少用多少平方厘米的布料,就是求这个圆柱形水杯的表面积,根据圆柱的表面积公式:表面积=底面积+侧面积,代入数据,即可解答。
【详解】3.14×(6÷2)2+3.14×6×14
=3.14×9+18.84×14
=28.26+263.76
=292.03(平方厘米)
答:妈妈至少用了292.02平方厘米布料。
答案第1页,共2页
答案第1页,共2页
六年级数学下册(北师大版)含答案
一、填空题
1.(如图)将圆柱形纸筒沿虚线剪开得到一个长方形,这个长方形的长是( )厘米,宽是( )厘米。(π取3.14)
(第1题) (第2题)
2.如图,是一个圆柱的侧面展开图,这个圆柱的表面积是( )。
3.一个无盖的圆柱形铁皮水桶,底面直径是20厘米,高是50厘米。做这样一个水桶,至少需要( )平方厘米铁皮。
4.一个圆柱,它的底面直径是6cm,比高多,这个圆柱的表面积是( )cm2。
5.一个圆柱的底面直径是4cm、高是18cm,这个圆柱的表面积是( )平方厘米。
6.把边长是8分米的正方形纸围成一个圆柱形纸筒(接头处不计),这个纸筒的侧面积是( )平方分米。
7.一种固体胶棒,它的底面周长是3.14厘米,高是6厘米,只包装它的侧面,包装一个需要( )平方厘米的包装纸。如果有1平方米的包装纸,最多能包装( )个固体胶棒。
8.一个圆柱的高增加2厘米,底面半径不变,表面积就增加了12.56平方厘米,则这个圆柱的底面周长是( )厘米。
9.一个底面周长为4cm的圆柱体侧面展开后是一个正方形,这个圆柱体的高是( )cm,这个正方形的面积是( )cm2。
二、选择题
10.一个圆柱体的侧面展开图是正方形,这个圆柱体的底面直径与高的比是( )。
A.2π∶1 B.1∶1 C.1∶π D.π∶1
11.将一个圆柱的侧面展开,一定得不到( )。
A.长方形 B.正方形 C.梯形
12.制作一个无盖的圆柱形水桶,有下图中几种型号的铁皮可供选择,一共可以搭配出( )种不同容积的水桶。
A.2 B.3 C.4 D.1
13.下面各图形中,( )是圆柱的展开图。(单位:cm)
A. B.
C. D.
14.一个圆柱,底面直径和高都是2分米,这个圆柱的侧面积是( )平方分米。
A.6π B.5π C.4π D.2π
15.一个圆柱形木棒,高是8分米,如果从上面将它的高截短,那么表面积比原来减少6.28平方分米,原来这根木棒的表面积是( )平方分米。
A.15.7 B.18.84 C.25.12 D.26.69
16.把一个棱长2分米的正方体削成一个最大的圆柱,这个圆柱的侧面积是( )。
A.18.84平方分米 B.6.28平方分米 C.3.14平方分米 D.12.56平方分米
17.一个圆柱的侧面展开图是一个正方形。这个圆柱的高是底面直径的( )倍。
A. B.2 C. D.
18.圆柱的侧面积的大小是由( )决定的。
A.底面半径 B.圆柱的高 C.底面半径和圆柱的高
19.用铁皮制作一个有盖的圆柱形油桶,底面半径是3分米,高与底面半径的比是2∶1。制作这个油桶至少需要( )平方分米的铁皮。
A.56.52 B.75.36 C.113.04 D.169.56
20.一个圆柱的底面周长是18.84米,高是2米,则这个圆柱的表面积是( )平方米。
A.94.2 B.65.94 C.56.52 D.37.68
21.(如图)同一个圆柱切分后,表面积比原来增加4rh的图是( )。
A.甲
B.乙
C.两个都是
D.两个都不是
三、判断题
22.一个圆柱的侧面沿高展开后恰好是一个正方形,圆柱的底面半径是2分米,圆柱的高是12.56分米。( )
23.,左图是一个圆柱的展开图。( )
24.圆柱的侧面展开可能是长方形,也可能是正方形。( )
25.圆柱底面半径扩大到原来的2倍,高不变,那么它的侧面积也随着扩大到原来的2倍。( )
26.一个圆柱体的高增加4厘米,它的表面积就比原来增加12.56平方厘米,则这个圆柱体的底面半径是1厘米。( )
27.一根长为1.5m的圆柱形木料,锯掉4dm长的一段后,表面积比原来减少了50.24dm2,这根木料原来的底面半径是2dm。( )
28.把一个圆柱平均切成3个小圆柱,那么每个小圆柱的表面积是原圆柱表面积的。( )
29.圆柱的底面半径扩大到原来的3倍,高不变,它的侧面积和底面积都扩大到原来的3倍。( )
四、图形计算
30.计算下图圆柱的表面积。
31.计算下面半个圆柱的表面积。
32.计算下面图形的表面积。
五、解答题
33.如图,用下面的长方形硬纸卷成圆柱形小笔筒,再给这个笔筒配一个底,想一想,还需要多少平方厘米的硬纸片?(请写出两种情况)
34.如图所示,明明和芳芳分别用纸剪下了两个相等的圆和一个长方形,想制作成圆柱。(单位:厘米)取
(1)他们两个剪下的图形都能围成圆柱吗?请在你认为可以围成圆柱的图下面画“√”。
(2)请计算围成的圆柱的表面积。
35.把下面圆柱的侧面沿高展开,得到的长方形长和宽各是几厘米?两个底面分别是多大的圆?在方格纸上画出这个圆柱的展开图。(每个方格边长1厘米)
36.会议大厅里有10根底面直径0.6米,高6米的圆柱形柱子,现在要在侧面刷上油漆,每平方米用油漆0.5千克,刷这些柱子要用油漆多少千克?(π≈3.14,结果取整数)
37.为了抗旱,东东家挖了一个从里面量底面直径为6米,深为2米的圆柱形蓄水池,现在要用水泥涂抹蓄水池的内壁与底部,以防止漏水。如果每平方米需要6千克水泥,涂抹这个蓄水池需要多少千克水泥?
38.做一个圆柱形铁皮水桶(无盖),高8分米,底面直径6分米,做这个水桶至少要用多少平方分米的铁皮?
39.一根长2米的圆柱木料,横着截去2分米,剩下的圆柱体的木料表面积比原来减少了12.56平方分米,原来圆柱体的表面积是多少平方分米?
40.妈妈给笑笑的水杯做了一个带底的敞口布套,如图所示。妈妈至少用了多少平方厘米布料?(接头处忽略不计)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1. 21.98 4
【分析】由图可知:圆柱的底面直径是7厘米,高是4厘米,将圆柱形纸筒沿虚线剪开得到一个长方形,根据圆柱侧面展开图的特征,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,根据圆的周长公式C=πd,代入数据解答即可。
【详解】由分析可知:
长方形的长:3.14×7=21.98(厘米)
长方形的宽=圆柱的高=4厘米
2.87.92
【分析】观察图形可知,圆柱的底面周长是12.56cm,高是5cm;根据圆的周长公式:周长=π×2×半径;半径=周长÷2÷π;代入数据,求出圆柱的底面半径;再根据圆柱的表面积公式:底面积×2+侧面积;代入数据,即可解答。
【详解】半径:12.56÷2÷3.14
=6.28÷3.14
=2(cm)
表面积:3.14×22×2+12.56×5
=3.14×4×2+62.8
=12.56×2+62.8
=25.12+62.8
=87.92(cm2)
3.3454
【分析】据题分析,做该水桶需要的铁皮,即是求该圆柱的表面积,圆柱的表面积为圆柱侧面积加上两个底面积,因为是无盖,没有上底面积,只需要用圆柱侧面积加上一个下底面积即可。根据圆柱侧面积公式,S=Ch,再根据圆的面积公式:S=r2,代入数值求解即可。
【详解】圆柱侧面积为:
20×3.14×50
=62.8×50
=3140(平方厘米)
底面积为:
3.14×(20÷2)2
=3.14×102
=3.14×100
=314(平方厘米)
共需要铁皮数:
3140+314=3454(平方厘米)
4.131.88
【分析】据题意可以求出圆柱的高是多少,再根据圆柱的表面积的公式=两个底面积+侧面积,可以求出圆柱的表面积是多少,列式解答即可。
【详解】6÷(1+)
=6×
=4(cm)
3.14×6×4+3.14×(6÷2)2×2
=3.14×24+3.14×18
=3.14×42
=131.88(cm2)
5.251.2
【分析】根据圆柱的表面积公式:表面积=侧面积+底面积×2,代入数据,即可解答。
【详解】3.14×4×18+3.14×(4÷2)2×2
=12.56×18+3.14×4×2
=226.08+12.56×2
=226.08+25.12
=251.2(平方厘米)
6.64
【分析】根据题意,因为接头处不计,所以围成纸筒的侧面积就等于这个正方形纸的面积,根据正方形的面积公式S=a×a,计算即可得到答案。
【详解】根据分析可知:
8×8=64(平方分米)
7. 18.84 530
【分析】根据圆柱的侧面积公式:S=ch,把数据代入公式解答,把1平方米换成10000平方厘米,看看10000平方厘米的里面有多少个18.84即可。
【详解】3.14×6=18.84(平方厘米)
1平方米=10000平方厘米
10000÷18.84=530(个)……14.8(平方厘米)
所以最多能包装530个固体胶棒。
8.6.28
【分析】根据题意可知,把圆柱的高增加2厘米,底面半径不变,表面积就增加了12.56平方厘米,表面积增加的是高为2厘米的圆柱的侧面积,根据圆柱的侧面积公式:S=Ch,那么C=S÷h,把数据代入公式解答。
【详解】12.56÷2=6.28(厘米),这个圆柱的底面周长是6.28厘米。
9. 4 16
【分析】圆柱的侧面展开后是正方形,说明圆柱的底面周长等于高。底面周长为4cm,则这个圆柱的高也是4cm。展开后的正方形的面积就是圆柱的侧面积,圆柱的侧面积=底面周长×高,据此代入数据计算。
【详解】一个底面周长为4cm的圆柱体侧面展开后是一个正方形,这个圆柱体的高是4cm;4×4=16(cm2),这个正方形的面积是16cm2。
10.C
【分析】一个圆柱体的侧面展开图是正方形,说明圆柱的底面周长与高相等,据此解答。
【详解】假设圆的底面直径为d,则圆柱的高为πd,
d∶πd=1∶π
故答案为:C
11.C
【分析】根据圆柱的侧面展开图的特点,将圆柱侧面的几种展开图方法与选项进行对比,即可进行选择。
【详解】圆柱的侧面沿高展开可能是长方形或正方形,如果斜着展开是一个平行四边形,因为圆柱的上下底面是完全相同的两个圆,所以圆柱的侧面展开图不可能是梯形。
故答案为:C
12.A
【分析】制作无盖的圆柱形水桶,说明要选一个长方形和一个圆形铁皮,而且所选的长方形的一条边和圆的周长相等即可达到要求;根据圆的周长公式:周长=π×直径,求出圆的周长,与长方形的长进行比较,即可解答。
【详解】③周长:3.14×4=12.56(dm)
④周长:3.14×3×2
=9.42×2
=18.84(dm)
⑤周长:3.14×3=9.42(dm)
①和⑤搭配;②和③搭配;
共2组。
故答案为:A
13.C
【分析】圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长方形(或正方形)的长等于圆柱底面的周长,依据圆的周长公式将数值代人计算并选择。
【详解】A.2×3.14=628(cm),6.28≠9.42,所以不是圆柱的展开图;
B.4×3.14=12.56(cm),12.56≠9.42,所以不是圆柱的展开图;
C.3×3.14=9.42(cm),9.42=9.42,所以是圆柱的展开图;
D.4×3.14=12.56(cm),12.56≠9.42所以不是圆柱的展开图。
故答案为:C
14.C
【分析】圆柱侧面积=,代数解答即可。
【详解】
这个圆柱的侧面积是平方分米。
故答案为:C
15.D
【分析】根据题意可知,一个圆柱形木棒,高是8分米,从上面将它的高截短,也就是把高截短8×=2(分米),表面积减少6.28平方分米,表面积减少的是高2分米的圆柱的侧面积,根据圆柱的侧面积=底面周长×高,据此可以求出底面周长,从而求出底面半径,再根据圆柱的表面积=侧面积+底面积×2,把数据代入公式解答。
【详解】底面周长:
6.28÷(8×)
=6.28÷2
=3.14(分米)
底面半径:3.14÷3.14÷2=0.5(分米)
原来这根木棒的表面积:
3.14×8+3.14×0.52×2
=25.12+3.14×0.25×2
=25.12+1.57
=26.69(平方分米)
故答案为:D
16.D
【分析】根据题意,棱长是2分米的正方体木块,削成一个最大的圆柱,则它的直径为2分米,高也为2分米,根据圆柱的侧面积公式S=Ch,计算即可解答。
【详解】3.14×2×2
=6.28×2
=12.56(平方分米)
故答案为:D
17.A
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的等于圆柱的底面周长,宽等于圆柱的高,如果圆柱的侧面展开图是一个正方形,那么这个圆柱的底面周长和高相等,根据圆的周长公式:,据此解答即可。
【详解】一个圆柱的侧面展开图是一个正方形。那么这个圆柱的底面周长和高相等,由圆周率的意义,=圆周率(),所以这个圆柱的高是底面直径的倍。
故答案为:A
18.C
【分析】圆柱的侧面积=底面周长×高,而底面周长=半径×2×圆周率,据此解答。
【详解】根据圆柱侧面积和圆的周长公式可知,圆柱的侧面积的大小是由底面半径和圆柱的高决定的。
故答案为:C
19.D
【分析】根据题意可知,高与底面半径的比是2∶1,即高是底面半径的2倍,用底面半径×2,求出高;求制作这个油桶至少需要的铁皮,就是求这个圆柱形油桶的表面积,根据圆柱的表面积公式:表面积=底面积×2+侧面积,代入数据,即可解答。
【详解】高:6×2=6(分米)
3.14×32×2+3.14×3×2×6
=3.14×9×2+9.42×2×6
=28.26×2+18.84×6
=56.52+113.04
=169.56(平方分米)
故答案为:D
20.A
【分析】圆柱的表面积=侧面积+底面积×2,而圆柱的侧面积=底面周长×高。已知圆柱的底面周长,先根据“圆的周长=2πr”求出圆柱的底面半径,再根据“圆的面积=πr2”可以求出圆柱的底面积。分别把数据代入公式求出侧面积和底面积,最后求出圆柱的表面积。
【详解】18.84÷3.14÷2=3(米)
18.84×2+3.14×33×2
=37.68+56.52
=94.2(平方米)
故答案为:A
21.B
【分析】观察图形可知,甲图增加的面积是2个半径为r的圆的面积,根据圆的面积公式:π×半径2,求出增加的面;乙图增加的面积是2个长是底面直径,宽是圆柱的高的长方形面积;根据长方形面积公式:长×宽;求出增加的面积,即可解答。
【详解】甲图增加的面积:
π×r2×2
=2πr2
乙图增加的面积:
r×2×h×2
=4rh
故答案为:B
22.√
【分析】由题意可知,圆柱的底面周长等于高,已知底面半径,求底面周长,即圆柱的高;根据圆的周长公式:C=2πr,代入数据解答即可作出判断。
【详解】2×3.14×2
=6.28×2
=12.56(分米)
故答案为:√
23.√
【分析】根据圆柱的表面组成和其侧面展开图的特点,对题中的图进行分析即可。
【详解】圆柱的表面由3部分组成:上下是两个大小相等的圆,沿圆柱的高展开,得到一个长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,如果不是沿着高剪开,是沿着一条斜线剪开,则是。
故答案为:√
24.√
【分析】圆柱的侧面展开图,如图、、,可能是长方形、正方形或平行四边形,据此分析。
【详解】圆柱的侧面沿高展开是长方形,当底面周长=高时,展开图是正方形,把圆柱侧面斜着剪开得到一个平行四边形,所以原题说法正确。
故答案为:√
25.√
【分析】圆柱的底面半径扩大到原来的2倍,则圆柱的底面周长也扩大到原来的2倍,圆柱的侧面积=底面周长×高,圆柱的高不变,则它的侧面积也扩大到原来的2倍,举例说明即可。
【详解】假设圆柱的底面半径为r,高为h,则扩大后的底面半径为2r。
=2
所以,圆柱的侧面积也扩大到原来的2倍。
故答案为:√
26.×
【分析】根据题意可知,增加部分就是高是4厘米的圆柱的侧面积;也就是一个长方形面积;长等于底面周长,宽等于4厘米;根据长方形面积公式:面积=长×宽;长=面积÷宽;代入数据,求出这个圆柱的底面周长;再根据圆的周长公式:周长=π×半径×2;半径=周长÷π÷2,代入数据,求出这个圆柱底面的半径,进行解答。
【详解】12.56÷4=3.14(厘米)
3.14÷3.14÷2
=1÷2
=0.5(厘米)
一个圆柱体的高增加4厘米,它的表面积就比原来增加12.56平方厘米,则这个圆柱体的底面半径是0.5厘米。
原题干说法错误。
故答案为:×
27.√
【分析】表面积减少部分是长为4分米的圆柱的侧面积,利用圆柱的侧面积=底面周长×高可以求得这个圆柱的底面周长,从而求得它的半径,据此解答即可。
【详解】圆柱的底面半径为:
50.24÷4÷3.14÷2
=12.56÷3.14÷2
=2(dm)
这根木料原来的底面半径是2dm。
故答案为:√
28.×
【分析】把一个圆柱平均切割成3个小圆柱,侧面积是原来圆柱侧面积的,但是底面积没变,据此分析。
【详解】圆柱表面积=底面积×2+侧面积,小圆柱表面积=底面积×2+侧面积×,小圆柱表面积不是原来圆柱表面积的。
故答案为:×
29.×
【分析】圆柱的底面半径扩大到原来的3倍,设原来的底面半径为r,高为h,它的底面积=πr2,侧面积=2πrh,底面半径扩大原来的3倍,它的底面积=π(3r)2=9πr2,侧面积=2×π(3r)×h,即可算出它们侧面积和底面积扩大几倍。
【详解】设底面半径为r,高为h
它的底面积=πr2,侧面积=2πrh;
半径扩大3倍,半径为3r,高是h
扩大后圆柱的底面积=π(3r)2=9πr2.,侧面积=2×π(3r)h=6πrh
9πr2÷πr2=9
底面积扩大到原来的9倍;
6πrh÷2πrh=3
它的侧面积扩大到原来的3倍;
原题说法错误。
故答案为:×
30.244.92dm2
【分析】根据圆柱的表面积=侧面积+底面积×2,圆柱的侧面积=底面周长×高,圆的面积公式:S=πr2,圆的周长公式:C=2πr,把数据代入公式解答。
【详解】3.14×(6÷2)2×2
=3.14×18
=56.52(dm2)
2×3.14×3×10
=18.84×10
=188.4(dm2)
56.52+188.4=244..92(dm2)
31.151.62dm2
【分析】由图可知:这个半圆柱的表面积包括一个长方形的面积,圆柱的侧面积的一半及上下两个半圆的面积之和就是一个底面积;根据圆柱的表面积公式:,其中,,,代入数据进行计算即可。
【详解】
32.1411.2cm2
【分析】根据图分析,该组合体表面积,由一个圆柱体表面积加一个长方体表面积,再减去二者重合的部分,为圆柱体的两个底面积,由此可得,该组合图形表面积即为一个长方体的表面积加上一个圆柱体的侧面积,据此解题即可。
【详解】长方体表面积为:
(20×15+15×8+20×8)×2
=(300+120+160)×2
=(420+160)×2
=(420+160)×2
=580×2
=1160(cm2)
圆柱侧积为:
3.14×10×8
=31.4×8
=251.2(cm2)
组合体表面积为:
1160+251.2=1411.2(cm2)
33.50.24平方厘米或12.56平方厘米
【分析】由题,长方形硬纸卷成圆柱形小笔筒有两种方法:以长为底面周长或者以宽为底面周长;根据圆的周长公式C=2πr,先分别求出两种情况下的底面半径r,再根据圆的面积公式S=π分别求出两种情况下的面积即可。
【详解】以长为底面周长时:
25.12÷3.14÷2
=8÷2
=4(厘米)
3.14×
=3.14×16
=50.24(平方厘米)
以宽为底面周长时:
12.56÷3.14÷2
=4÷2
=2(厘米)
3.14×
=3.14×4
=12.56(平方厘米)
答:还需要50.24平方厘米或12.56平方厘米的硬纸片。
34.(1)明明能,芳芳不能;图见详解
(2)51.81平方厘米
【分析】(1)根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。根据圆的周长公式分别求出直径是3厘米、直径是5厘米的两个圆的周长,分别和两个长方形的长进行比较,如果圆的周长等于长方形的长,说明能围成圆柱,否则就不能围成圆柱。据此判断即可。
(2)根据圆柱的表面积=侧面积+底面积×2,把数据代入公式解答。
【详解】(1)明明剪下的圆的周长:
(厘米)
9.42厘米厘米
芳芳剪下的圆的周长:
(厘米)
15.7厘米≠8厘米≠5厘米
所以明明剪下的图形可以围成一个圆柱。
(2)
(平方厘米)
答:这个圆柱的表面积是51.81平方厘米。
35.长6.28;宽2厘米;两个直径为2厘米的圆;画图见详解
【分析】应明确圆柱由三部分组成:圆柱的侧面、圆柱的上、下两个底面;由题意可知:该圆柱的底面直径是2厘米,高为2厘米,根据“圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高”可知:先根据圆的周长=πd求出圆柱侧面展开后的长,宽为圆柱的高;圆柱的上下两个底面是直径为2厘米的圆,画出即可。
【详解】长方形的长:3.14×2=6.28(厘米)
长方形的宽是:2厘米
两个底面是两个直径为2厘米的圆。
据此画图如下:
36.56.52千克
【分析】圆柱侧面积=,代数求出一根柱子的侧面积,然后乘10求出10根侧面积,最后乘每平方米所用油漆量即可解答。
【详解】3.14×0.6×6×10×0.5
=11.304×10×0.5
=56.52(千克)
答:刷这些柱子要用油漆56.52千克。
37.395.64千克
【分析】由题意,抹水泥的是圆柱侧面积和一个底面积,根据公式计算出面积,再乘6即可。
【详解】
(千克)
答:涂抹这个蓄水池需要395.64千克水泥。
38.178.98平方分米
【分析】首先分清制作没有盖的圆柱形铁皮水桶,需要计算几个面的面积:侧面面积与底面圆的面积,由圆柱体侧面积和圆的面积计算方法解答即可。
【详解】3.14×+3.14×6×8
=3.14×9+3.14×48
=3.14×57
=178.98(平方分米)
答:做这个水桶至少要用178.98平方分米的铁皮。
39.131.88平方分米
【分析】由题意知,截去的部分是一个高为2分米的圆柱体,并且表面积减少了12.56平方分米,其实减少的面积就是截去部分的侧面积,由此可求出圆柱体的底面周长,进一步可求出底面积是多少,利用表面积=底面积×2+底面周长×高,即可求出这个圆柱的表面积。
【详解】底面周长:12.56÷2=6.28(分米)
底面半径:6.28÷3.14÷2
=2÷2
=1(分米)
底面积:3.14×12
=3.14×1
=3.14(平方分米)
2米=20分米
表面积:6.28×20+3.14×2
=125.6+6.28
=131.88(平方分米)
答:原来圆柱体的表面积是131.88平方分米。
40.292.02平方厘米
【分析】求至少用多少平方厘米的布料,就是求这个圆柱形水杯的表面积,根据圆柱的表面积公式:表面积=底面积+侧面积,代入数据,即可解答。
【详解】3.14×(6÷2)2+3.14×6×14
=3.14×9+18.84×14
=28.26+263.76
=292.03(平方厘米)
答:妈妈至少用了292.02平方厘米布料。
答案第1页,共2页
答案第1页,共2页
