2022-2023学年人教版数学八年级下册 17.2勾股定理的逆定理 同步练习 (无答案)
文档属性
| 名称 | 2022-2023学年人教版数学八年级下册 17.2勾股定理的逆定理 同步练习 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 148.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 00:00:00 | ||
图片预览

文档简介
17.2勾股定理的逆定理
一、选择题
下列条件中能构成直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
在下列四组数中,不是勾股数的一组数是
A.,, B.,,
C.,, D.,,
已知 ,, 是三角形的三边长,如果满足 ,那么下列说法中不正确的是
A.这个三角形是直角三角形
B.这个三角形的最长边长是
C.这个三角形的面积是
D.这个三角形的最长边上的高是
已知 的三边分别是 ,,,则 的面积是
A. B. C. D.
两个边长分别为 ,, 的直角三角形和一个两条直角边都是 的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为
A. B.
C. D.
在 中,,, 的对边分别是 ,,,下列命题中的假命题是
A.若 ,则
B.若 ,则 不是直角三角形
C.若 ,则
D.若 ,则
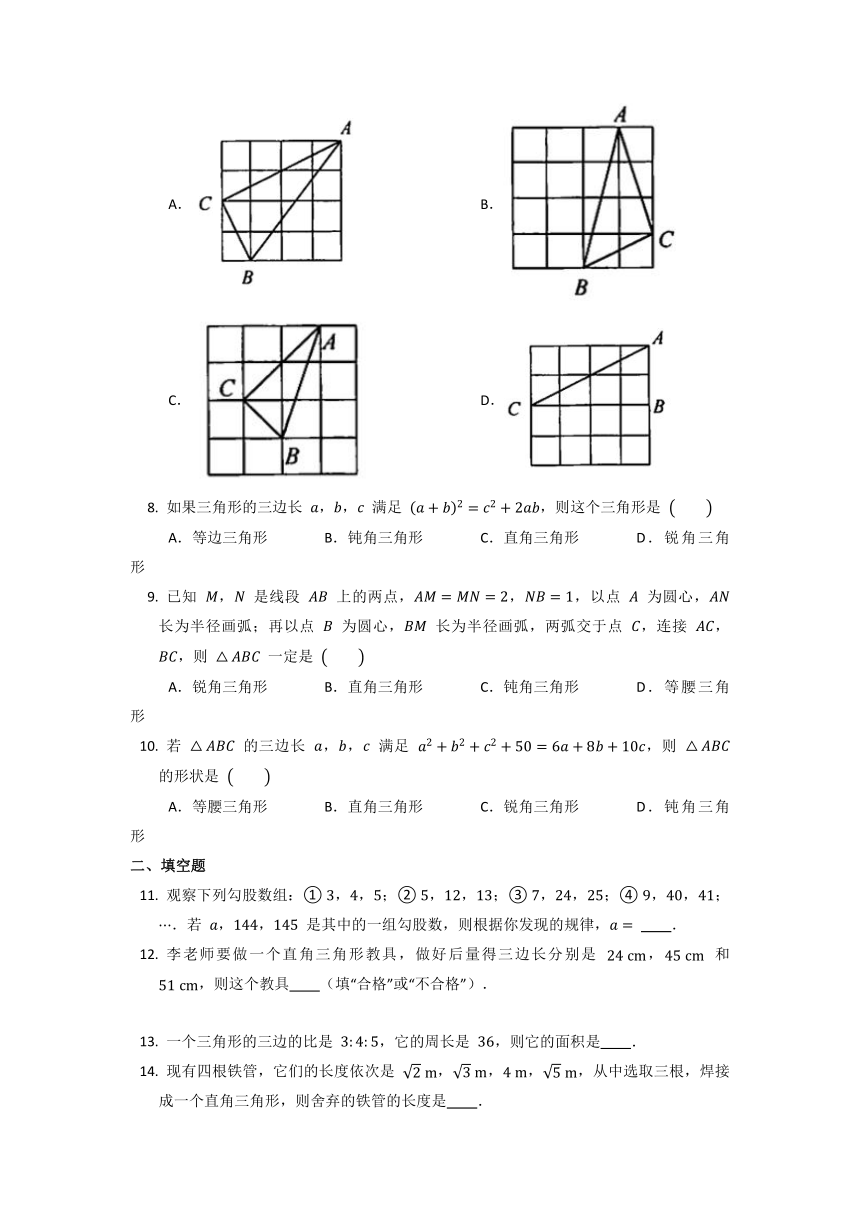
如图,在四个均由十六个小正方形组成的正方形网格中,各有一个 ,那么在这四个三角形中,不是直角三角形的是
A. B.
C. D.
如果三角形的三边长 ,, 满足 ,则这个三角形是
A.等边三角形 B.钝角三角形 C.直角三角形 D.锐角三角形
已知 , 是线段 上的两点,,,以点 为圆心, 长为半径画弧;再以点 为圆心, 长为半径画弧,两弧交于点 ,连接 ,,则 一定是
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
若 的三边长 ,, 满足 ,则 的形状是
A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
二、填空题
观察下列勾股数组:① ,,;② ,,;③ ,,;④ ,,;.若 ,, 是其中的一组勾股数,则根据你发现的规律, .
李老师要做一个直角三角形教具,做好后量得三边长分别是 , 和 ,则这个教具 (填“合格”或“不合格”).
一个三角形的三边的比是 ,它的周长是 ,则它的面积是 .
现有四根铁管,它们的长度依次是 ,,,,从中选取三根,焊接成一个直角三角形,则舍弃的铁管的长度是 .
如图所示为一块农家菜地的平面图,其中 ,,,,,则这块菜地的面积为 .
的三边分别为 ,,,且满足关系 ,则
是 三角形.
三、解答题
如图,在边长为 的小正方形组成的网格中, 的三个顶点均在格点上,请按要求完成下列各题:
(1) 画线段 且使 ,连接 ;
(2) 线段 的长为 , 的长为 , 的长为 ;
(3) 为 三角形,四边形 的面积为 .
已知 的三边长 ,, 满足条件 ,试判断 的形状.
如图,某港口 位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行 海里,“海天”号每小时航行 海里.它们离开港口一小时后分别位于点 , 处,且相距 海里.如果知道“远航”号沿北偏东 方向航行,你能判断“海天”号沿哪个方向航行吗?请说明理由.
阅读下列一段文字,然后回答下列问题.
已知平面内两点 ,,则这两点间的距离可用下列公式计算:.
例如:已知 ,,则这两点间的距离 ,特别地,如果两点 、 所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为 或 .
(1) 已知 ,,求 , 两点间的距离.
(2) 已知 , 在平行于 轴的同一条直线上,点 的纵坐标为 ,点 的纵坐标为 ,求 , 两点间的距离;
(3) 已知 的顶点坐标分别为 、 ,,你能判定 的形状吗?请说明理由.
一、选择题
下列条件中能构成直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
在下列四组数中,不是勾股数的一组数是
A.,, B.,,
C.,, D.,,
已知 ,, 是三角形的三边长,如果满足 ,那么下列说法中不正确的是
A.这个三角形是直角三角形
B.这个三角形的最长边长是
C.这个三角形的面积是
D.这个三角形的最长边上的高是
已知 的三边分别是 ,,,则 的面积是
A. B. C. D.
两个边长分别为 ,, 的直角三角形和一个两条直角边都是 的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为
A. B.
C. D.
在 中,,, 的对边分别是 ,,,下列命题中的假命题是
A.若 ,则
B.若 ,则 不是直角三角形
C.若 ,则
D.若 ,则
如图,在四个均由十六个小正方形组成的正方形网格中,各有一个 ,那么在这四个三角形中,不是直角三角形的是
A. B.
C. D.
如果三角形的三边长 ,, 满足 ,则这个三角形是
A.等边三角形 B.钝角三角形 C.直角三角形 D.锐角三角形
已知 , 是线段 上的两点,,,以点 为圆心, 长为半径画弧;再以点 为圆心, 长为半径画弧,两弧交于点 ,连接 ,,则 一定是
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
若 的三边长 ,, 满足 ,则 的形状是
A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
二、填空题
观察下列勾股数组:① ,,;② ,,;③ ,,;④ ,,;.若 ,, 是其中的一组勾股数,则根据你发现的规律, .
李老师要做一个直角三角形教具,做好后量得三边长分别是 , 和 ,则这个教具 (填“合格”或“不合格”).
一个三角形的三边的比是 ,它的周长是 ,则它的面积是 .
现有四根铁管,它们的长度依次是 ,,,,从中选取三根,焊接成一个直角三角形,则舍弃的铁管的长度是 .
如图所示为一块农家菜地的平面图,其中 ,,,,,则这块菜地的面积为 .
的三边分别为 ,,,且满足关系 ,则
是 三角形.
三、解答题
如图,在边长为 的小正方形组成的网格中, 的三个顶点均在格点上,请按要求完成下列各题:
(1) 画线段 且使 ,连接 ;
(2) 线段 的长为 , 的长为 , 的长为 ;
(3) 为 三角形,四边形 的面积为 .
已知 的三边长 ,, 满足条件 ,试判断 的形状.
如图,某港口 位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行 海里,“海天”号每小时航行 海里.它们离开港口一小时后分别位于点 , 处,且相距 海里.如果知道“远航”号沿北偏东 方向航行,你能判断“海天”号沿哪个方向航行吗?请说明理由.
阅读下列一段文字,然后回答下列问题.
已知平面内两点 ,,则这两点间的距离可用下列公式计算:.
例如:已知 ,,则这两点间的距离 ,特别地,如果两点 、 所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为 或 .
(1) 已知 ,,求 , 两点间的距离.
(2) 已知 , 在平行于 轴的同一条直线上,点 的纵坐标为 ,点 的纵坐标为 ,求 , 两点间的距离;
(3) 已知 的顶点坐标分别为 、 ,,你能判定 的形状吗?请说明理由.
