6.1平方根(算术平方根)(省一等奖课件)
文档属性
| 名称 | 6.1平方根(算术平方根)(省一等奖课件) |  | |
| 格式 | zip | ||
| 文件大小 | 879.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-18 12:28:38 | ||
图片预览




文档简介
课件16张PPT。义务教育教科书(数学)七年级下册第六章算术平方根 在我校举行的绘画比赛中,欢欢同学准备了一些正方形的画布,你能计算出它们的面积吗?
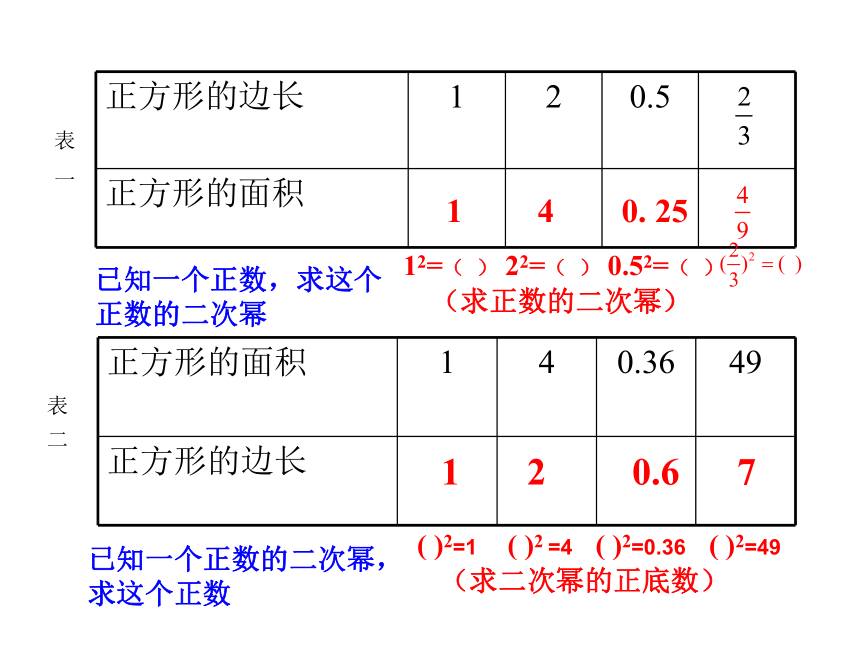
1 4 0. 2512=( )22=( )0.52= ( )表 一已知一个正数,求这个正数的二次幂(求正数的二次幂)一、创设情境、引入新知 ( )2=1 ( )2 =4 ( )2=0.36 ( )2=49(求二次幂的正底数)已知一个正数的二次幂,求这个正数表 二表一和表二中的两种运算有什么关系?1 2 0.6 7 12=( ) 22=( ) 0.52=( ) 表 一表 二 已知一个正数,求这个正数的二次幂已知一个正数的二次幂,求这个正数1 4 0. 25 1 2 0.6 7 ( )2=1 ( )2 =4 ( )2=0.36 ( )2=49(求正数的二次幂)(求二次幂的正底数)
如果正方形的边长用x表示,面积用a表示,就可以得到x2=a,那么x就是求正数的二次幂运算x2=a中的逆运算。你能用自己的语言叙述求正数的二次幂运算的逆运算吗?一般地,如果一个正数x的平方等于a,即x2=a,
那么这个正数x就叫做a的算术平方根.
(实际上,正数x就是二次幂运算x2=a中的正底数)
二、形成概念、类比理解特别地,我们规定0的算术平方根是0. 试一试
(1) 因为22=4 ,所以4的算术平方根是__;
(2) 因为0.52=0.25 ,所以0.25的算术平方根是__;
(3) 因为 = ,所以 的算术平方根是 ;20.5想一想:判断下列说法是否正确。
①5是25的算术平方根 ( );
②0.01是0.1的算术平方根 ( );
③0的算术平方根是它本身 ( )。√√三、初步应用、体验成功a的算术平方根 互为
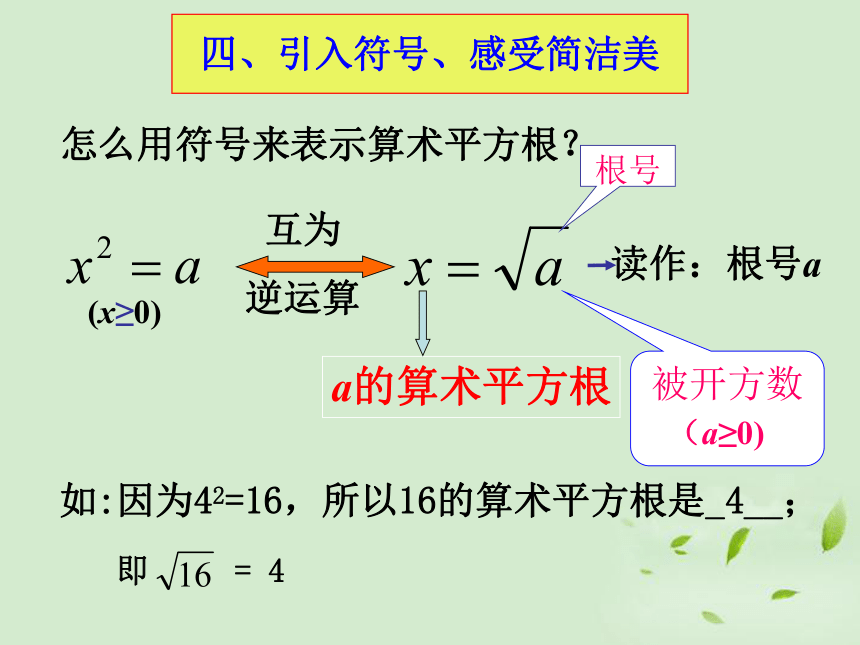
逆运算根号被开方数读作:根号a(a≥0)四、引入符号、感受简洁美怎么用符号来表示算术平方根?(x≥0)
如:因为42=16,所以16的算术平方根是_4__; 即 = 4 例1:求下列各数的算术平方根
(1)100 (2)0.04 (3) (4) 0
解:(1)
因为 102=100,
所以100的算术平方根是10,
即 =10.
四、引入符号、感受简洁美
1、观察下列计算过程:算术平方根的性质:(1)正数有一个正的算术平方根;
(2)算术平方根等于它本身的数是0和1;
(3)被平方数越大,对应的算术平方根也越大。(1)因为12=1 ,所以 =1 ;
(2)因为112=121 ,所以 =11 ;
(3)因为1112=12321 ,所以 =111 ; … … 由此猜想: =___________________. 填空:(看谁算得又对又快)
(1) 一个数的算术平方根是3,则这个数是_______.
(2) 一个自然数的算术平方根为a,则这个自然数是___________;和这个自然数相邻的下一个自然数是 _____________。
(3) 的算术平方根为_______.
(4) 2 的算术平方根为________.
+139
到底有多大?
你认为它在哪两个整数之间? 五、感知估算、扩大认识 “小数学家”妮妮就想到了一个办法:
①用 -1 来表示 的小数部分,你同意妮妮的表示方法吗?请说明理由.
②类似地, 的小数部分可以表示为_________;
的小数部分可以表示为_________;③如果 的整数部分用m来表示,小数部分用n来表示,那么m、n分别是______,______.
-1-2五、感知估算、扩大认识3-3是有限小数吗? (它是一个小数位数无限,且小数部分不循环的小数.这样的数我们称之为无限不循环小数.)
你以前见过这种数吗?它们是有理数吗?π
自由下落物体的高度h(米)与下落时间t(秒)的关系为h=4.9t2有一铁球从19.6 米高的建筑物上自由下落,到达地面需要多长时间 ?六、学以致用、强化新知(1)本节课你学习了哪些知识?
(2)在探索知识的过程中,你积累了哪些经验?这节课主要学习了算术平方根的概念和表示方法,知道了求一个正数的算术平方根与求一个正数的二次幂正好是互逆的过程,因此,求正数的算术平方根实际上可以转化为求一个数的二次幂运算. 只不过,只有正数和0才有算术平方根.七、小结提升、合作交流思维方法:求一个正数的算术平方根运算和开平方求一个正数的二次幂运算互为逆运算。
探究策略:由特殊到一般,再由一般到特殊,是发现问题和解决 问题的基本方法和途径。八、分层作业、共同进步 1.必做题: 习题6.1第1题,第2题。?
2.选做题:
(1)已知 ,求 的值;
(2)3x-4为25的算术平方根,求x的值。
3.课外知识阅读:见学案材料 亲爱的同学们,当你为生活、学习的山重水复而愁眉苦脸时,不妨换一种方法看问题,或许,你会收获一个柳暗花明的美好心情.希望各位在今后的学习中,能善于发现,勇于探索,敢于创新!
1 4 0. 2512=( )22=( )0.52= ( )表 一已知一个正数,求这个正数的二次幂(求正数的二次幂)一、创设情境、引入新知 ( )2=1 ( )2 =4 ( )2=0.36 ( )2=49(求二次幂的正底数)已知一个正数的二次幂,求这个正数表 二表一和表二中的两种运算有什么关系?1 2 0.6 7 12=( ) 22=( ) 0.52=( ) 表 一表 二 已知一个正数,求这个正数的二次幂已知一个正数的二次幂,求这个正数1 4 0. 25 1 2 0.6 7 ( )2=1 ( )2 =4 ( )2=0.36 ( )2=49(求正数的二次幂)(求二次幂的正底数)
如果正方形的边长用x表示,面积用a表示,就可以得到x2=a,那么x就是求正数的二次幂运算x2=a中的逆运算。你能用自己的语言叙述求正数的二次幂运算的逆运算吗?一般地,如果一个正数x的平方等于a,即x2=a,
那么这个正数x就叫做a的算术平方根.
(实际上,正数x就是二次幂运算x2=a中的正底数)
二、形成概念、类比理解特别地,我们规定0的算术平方根是0. 试一试
(1) 因为22=4 ,所以4的算术平方根是__;
(2) 因为0.52=0.25 ,所以0.25的算术平方根是__;
(3) 因为 = ,所以 的算术平方根是 ;20.5想一想:判断下列说法是否正确。
①5是25的算术平方根 ( );
②0.01是0.1的算术平方根 ( );
③0的算术平方根是它本身 ( )。√√三、初步应用、体验成功a的算术平方根 互为
逆运算根号被开方数读作:根号a(a≥0)四、引入符号、感受简洁美怎么用符号来表示算术平方根?(x≥0)
如:因为42=16,所以16的算术平方根是_4__; 即 = 4 例1:求下列各数的算术平方根
(1)100 (2)0.04 (3) (4) 0
解:(1)
因为 102=100,
所以100的算术平方根是10,
即 =10.
四、引入符号、感受简洁美
1、观察下列计算过程:算术平方根的性质:(1)正数有一个正的算术平方根;
(2)算术平方根等于它本身的数是0和1;
(3)被平方数越大,对应的算术平方根也越大。(1)因为12=1 ,所以 =1 ;
(2)因为112=121 ,所以 =11 ;
(3)因为1112=12321 ,所以 =111 ; … … 由此猜想: =___________________. 填空:(看谁算得又对又快)
(1) 一个数的算术平方根是3,则这个数是_______.
(2) 一个自然数的算术平方根为a,则这个自然数是___________;和这个自然数相邻的下一个自然数是 _____________。
(3) 的算术平方根为_______.
(4) 2 的算术平方根为________.
+139
到底有多大?
你认为它在哪两个整数之间? 五、感知估算、扩大认识 “小数学家”妮妮就想到了一个办法:
①用 -1 来表示 的小数部分,你同意妮妮的表示方法吗?请说明理由.
②类似地, 的小数部分可以表示为_________;
的小数部分可以表示为_________;③如果 的整数部分用m来表示,小数部分用n来表示,那么m、n分别是______,______.
-1-2五、感知估算、扩大认识3-3是有限小数吗? (它是一个小数位数无限,且小数部分不循环的小数.这样的数我们称之为无限不循环小数.)
你以前见过这种数吗?它们是有理数吗?π
自由下落物体的高度h(米)与下落时间t(秒)的关系为h=4.9t2有一铁球从19.6 米高的建筑物上自由下落,到达地面需要多长时间 ?六、学以致用、强化新知(1)本节课你学习了哪些知识?
(2)在探索知识的过程中,你积累了哪些经验?这节课主要学习了算术平方根的概念和表示方法,知道了求一个正数的算术平方根与求一个正数的二次幂正好是互逆的过程,因此,求正数的算术平方根实际上可以转化为求一个数的二次幂运算. 只不过,只有正数和0才有算术平方根.七、小结提升、合作交流思维方法:求一个正数的算术平方根运算和开平方求一个正数的二次幂运算互为逆运算。
探究策略:由特殊到一般,再由一般到特殊,是发现问题和解决 问题的基本方法和途径。八、分层作业、共同进步 1.必做题: 习题6.1第1题,第2题。?
2.选做题:
(1)已知 ,求 的值;
(2)3x-4为25的算术平方根,求x的值。
3.课外知识阅读:见学案材料 亲爱的同学们,当你为生活、学习的山重水复而愁眉苦脸时,不妨换一种方法看问题,或许,你会收获一个柳暗花明的美好心情.希望各位在今后的学习中,能善于发现,勇于探索,敢于创新!
