2022-2023学年苏科版七年级数学下册 7.2探索平行线的性质 自主提升训练题 (无答案)
文档属性
| 名称 | 2022-2023学年苏科版七年级数学下册 7.2探索平行线的性质 自主提升训练题 (无答案) |

|
|
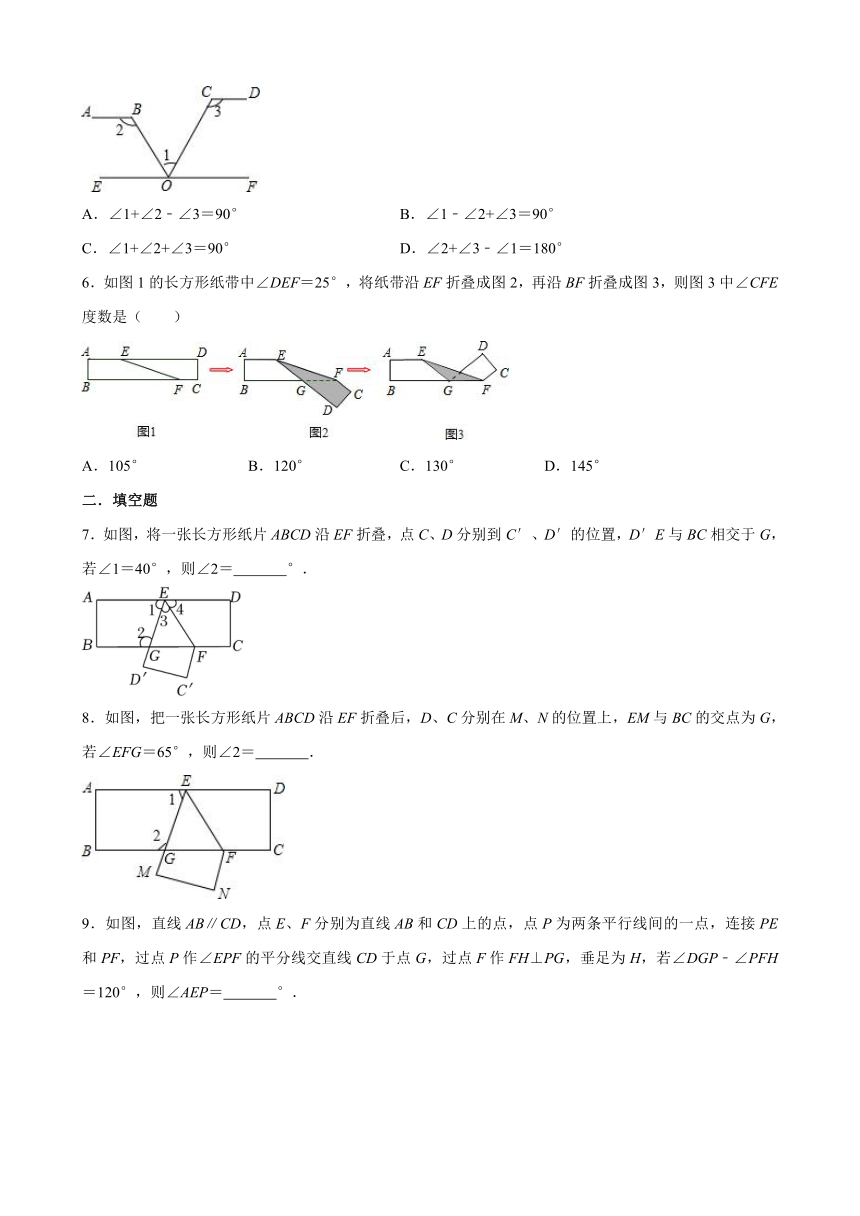
| 格式 | docx | ||
| 文件大小 | 189.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 00:00:00 | ||
图片预览


文档简介
《7.2探索平行线的性质》自主提升训练题
一.选择题
1.如图,若l1∥l2,l3∥l4,若∠1=110°,则∠2的度数为( )
A.70° B.80° C.90° D.110°
2.已知直线a∥b,将一块含30°角的直角三角板(∠BAC=30°,∠ACB=90°)按如图所示的方式放置,并且顶点A,C分别落在直线a,b上,若∠1=22°.则∠2的度数是( )
A.38° B.45° C.52° D.58°
3.如图,直线m∥n,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若∠1=60°,则下列结论正确的是( )
A.∠2=65° B.∠3=45° C.∠4=125° D.∠5=130°
4.如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( )
A.40° B.50° C.140° D.150°
5.如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2﹣∠3=90° B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=90° D.∠2+∠3﹣∠1=180°
6.如图1的长方形纸带中∠DEF=25°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是( )
A.105° B.120° C.130° D.145°
二.填空题
7.如图,将一张长方形纸片ABCD沿EF折叠,点C、D分别到C′、D′的位置,D′E与BC相交于G,若∠1=40°,则∠2= °.
8.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=65°,则∠2= .
9.如图,直线AB∥CD,点E、F分别为直线AB和CD上的点,点P为两条平行线间的一点,连接PE和PF,过点P作∠EPF的平分线交直线CD于点G,过点F作FH⊥PG,垂足为H,若∠DGP﹣∠PFH=120°,则∠AEP= °.
10.如图所示,△ABC中∠C=60°,AC边上有一点D,使得∠A=∠ABD,将△ABC沿BD翻折得△A'BD,此时A'D∥BC,则∠ABC= 度.
11.如图,是某课题学习小组对地图上的A、B、E、F、G、H、P、C八处地点进行观察、分析.在讨论中得到了∠B=∠C=60°,F、H都在线段BC上,EF∥GH∥AC,PH∥GF∥AB的正确结论.接着,小聪又提出了如下结论线路B→A→C与线路B→E→F→G→H→P→C一样长.请判断小聪提出的结论正确吗? (填“正确”或“错误”).
12如图把一个长方形纸片沿EF折叠后,点D、C分别落在D'、C'处,∠AED'=40°,则∠BFC′= .
12.如图,已知CF∥AG,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠2=58°.
(1)求∠ACE的度数;
(2)若∠1=32°,说明:AB∥CD.
13.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是过点P作PE∥AB,通过平行线的性质来求∠APC.
(1)按照小明的思路,则∠APC的度数为 .
(2)问题迁移:如图2,AB∥CD,点P在射线ON上运动,记∠PAB=α,∠PCD=β.当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P不在B、D两点之间运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
三.解答题
14(1)如图(1),AB∥EF.求证:∠BCF=∠B+∠F.
(2)当点C在直线BF的右侧时,如图(2),若AB∥EF,则∠BCF与∠B、∠F的关系如何?请说明理由.
15.爱国同学在完成七年级下册数学的学习后,遇到了一些问题,聪明的你,帮他解决一下.
(1)如图1,已知AB∥CD,则∠AMC=∠BAM+∠DCM成立吗?请你帮他说明理由;
(2)如图2,已知AB∥CD,BM平分∠ABC,DM平分∠ADC.BM、DM所在直线交于点M,若∠NAD=64°,∠ABC=44°,请你帮他求∠BMD的度数;
(3)将图2中的点B移到点A的右侧,得到图3,其他条件不变,若∠NAD=α°,∠ABC=β°,请你帮他求出∠BMD的度数(用含α,β的式子表示).
16.已知AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一动点P.
(1)如图1所示时,试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?并说明理由.
(2)除了(1)的结论外,试问∠AEP,∠EPF,∠PFC还可能满足怎样的数量关系?请画图并证明;
(3)当∠EPF满足0°<∠EPF<180°,且QE,QF分别平分∠PEB和∠PFD,
①若∠EPF=60°,则∠EQF= °.
②猜想∠EPF与∠EQF的数量关系.(直接写出结论)
17.已知:如图,点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D、F,点M、G在AB上,∠AMD=∠AGF,∠1=∠2.
求证:∠DMB+∠ABC=180°.
小勇在做上面这道题时用了以下推理过程.请帮他在横线上填写结论,在括号内填写推理依据.
证明:∵BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
∴∠BDC=90°,∠EFC=90° ( ).
∴∠BDC=∠EFC(等量代换).
∴ (同位角相等,两直线平行).
∴∠CBD=∠2 .
∵∠1=∠2(已知).
∴∠CBD=∠1 ( ).
∴ ( ).
∵∠AMD=∠AGF(已知).
∴GF∥MD(同位角相等,两直线平行).
∴BC∥MD ( ).
∴∠DMB+∠ABC=180° ( ).
一.选择题
1.如图,若l1∥l2,l3∥l4,若∠1=110°,则∠2的度数为( )
A.70° B.80° C.90° D.110°
2.已知直线a∥b,将一块含30°角的直角三角板(∠BAC=30°,∠ACB=90°)按如图所示的方式放置,并且顶点A,C分别落在直线a,b上,若∠1=22°.则∠2的度数是( )
A.38° B.45° C.52° D.58°
3.如图,直线m∥n,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若∠1=60°,则下列结论正确的是( )
A.∠2=65° B.∠3=45° C.∠4=125° D.∠5=130°
4.如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( )
A.40° B.50° C.140° D.150°
5.如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2﹣∠3=90° B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=90° D.∠2+∠3﹣∠1=180°
6.如图1的长方形纸带中∠DEF=25°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是( )
A.105° B.120° C.130° D.145°
二.填空题
7.如图,将一张长方形纸片ABCD沿EF折叠,点C、D分别到C′、D′的位置,D′E与BC相交于G,若∠1=40°,则∠2= °.
8.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=65°,则∠2= .
9.如图,直线AB∥CD,点E、F分别为直线AB和CD上的点,点P为两条平行线间的一点,连接PE和PF,过点P作∠EPF的平分线交直线CD于点G,过点F作FH⊥PG,垂足为H,若∠DGP﹣∠PFH=120°,则∠AEP= °.
10.如图所示,△ABC中∠C=60°,AC边上有一点D,使得∠A=∠ABD,将△ABC沿BD翻折得△A'BD,此时A'D∥BC,则∠ABC= 度.
11.如图,是某课题学习小组对地图上的A、B、E、F、G、H、P、C八处地点进行观察、分析.在讨论中得到了∠B=∠C=60°,F、H都在线段BC上,EF∥GH∥AC,PH∥GF∥AB的正确结论.接着,小聪又提出了如下结论线路B→A→C与线路B→E→F→G→H→P→C一样长.请判断小聪提出的结论正确吗? (填“正确”或“错误”).
12如图把一个长方形纸片沿EF折叠后,点D、C分别落在D'、C'处,∠AED'=40°,则∠BFC′= .
12.如图,已知CF∥AG,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠2=58°.
(1)求∠ACE的度数;
(2)若∠1=32°,说明:AB∥CD.
13.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是过点P作PE∥AB,通过平行线的性质来求∠APC.
(1)按照小明的思路,则∠APC的度数为 .
(2)问题迁移:如图2,AB∥CD,点P在射线ON上运动,记∠PAB=α,∠PCD=β.当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P不在B、D两点之间运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
三.解答题
14(1)如图(1),AB∥EF.求证:∠BCF=∠B+∠F.
(2)当点C在直线BF的右侧时,如图(2),若AB∥EF,则∠BCF与∠B、∠F的关系如何?请说明理由.
15.爱国同学在完成七年级下册数学的学习后,遇到了一些问题,聪明的你,帮他解决一下.
(1)如图1,已知AB∥CD,则∠AMC=∠BAM+∠DCM成立吗?请你帮他说明理由;
(2)如图2,已知AB∥CD,BM平分∠ABC,DM平分∠ADC.BM、DM所在直线交于点M,若∠NAD=64°,∠ABC=44°,请你帮他求∠BMD的度数;
(3)将图2中的点B移到点A的右侧,得到图3,其他条件不变,若∠NAD=α°,∠ABC=β°,请你帮他求出∠BMD的度数(用含α,β的式子表示).
16.已知AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一动点P.
(1)如图1所示时,试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?并说明理由.
(2)除了(1)的结论外,试问∠AEP,∠EPF,∠PFC还可能满足怎样的数量关系?请画图并证明;
(3)当∠EPF满足0°<∠EPF<180°,且QE,QF分别平分∠PEB和∠PFD,
①若∠EPF=60°,则∠EQF= °.
②猜想∠EPF与∠EQF的数量关系.(直接写出结论)
17.已知:如图,点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D、F,点M、G在AB上,∠AMD=∠AGF,∠1=∠2.
求证:∠DMB+∠ABC=180°.
小勇在做上面这道题时用了以下推理过程.请帮他在横线上填写结论,在括号内填写推理依据.
证明:∵BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
∴∠BDC=90°,∠EFC=90° ( ).
∴∠BDC=∠EFC(等量代换).
∴ (同位角相等,两直线平行).
∴∠CBD=∠2 .
∵∠1=∠2(已知).
∴∠CBD=∠1 ( ).
∴ ( ).
∵∠AMD=∠AGF(已知).
∴GF∥MD(同位角相等,两直线平行).
∴BC∥MD ( ).
∴∠DMB+∠ABC=180° ( ).
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
