5.3.1函数的单调性(第一课时) 课件(共31张PPT)
文档属性
| 名称 | 5.3.1函数的单调性(第一课时) 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 47.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 12:49:33 | ||
图片预览








文档简介
(共31张PPT)
第五章一元函数的导数及其应用
5.3.1函数的单调性(第一课时)
李思
2022
目录
CONTENTS
知识回顾
课堂总结
典型例题
函数的单调性
01
02
03
04
RART 01
知识回顾
知识回顾
1.函数单调性的定义是什么?
对于给定区间D上的函数f(x),若对于属于区间D的任意两个自变量的值x1,x2,
当x1若f(x1)若f(x1)>f(x2),那么f(x)在这个区间上是减函数.
在必修第一册中, 我们通过图象直观,利用不等式、方程等知识,研究了函数的单调性、周期性、奇偶性以及最大(小)值等性质.
在本章前两节中,我们学习了导数的概念和运算,知道导数定量地刻画了函数的局部变化. 能否利用导数更加精确地研究函数的性质呢 本节我们就来讨论这个问题.
RART 02
函数的单调性与导数
函数的单调性
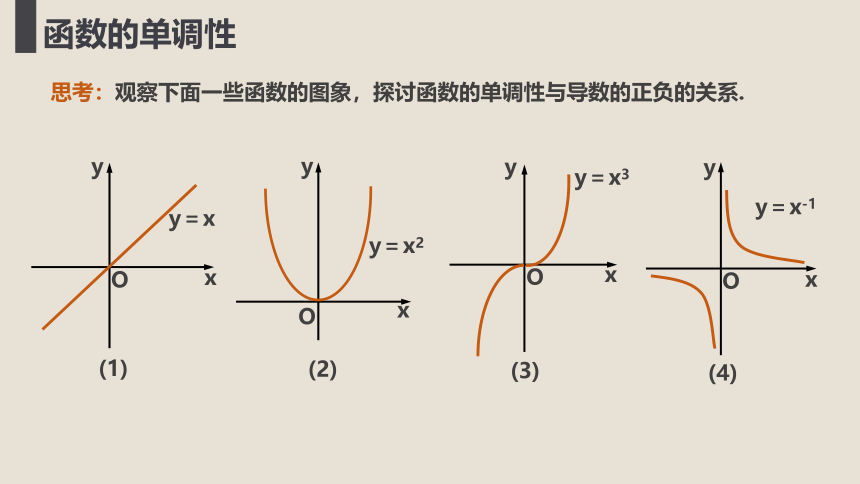
思考:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
x
y
O
y=x
(1)
x
y
O
y=x2
(2)
x
y
O
y=x3
(3)
x
y
O
(4)
y=x-1
函数的单调性
思考:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
x
y
O
y=x
(1)
在(-∞, +∞)上, f (x)单调递增
在(-∞, +∞)上,f ′ (x)>0
x
y
O
y′=1
函数的单调性
思考:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
x
y
O
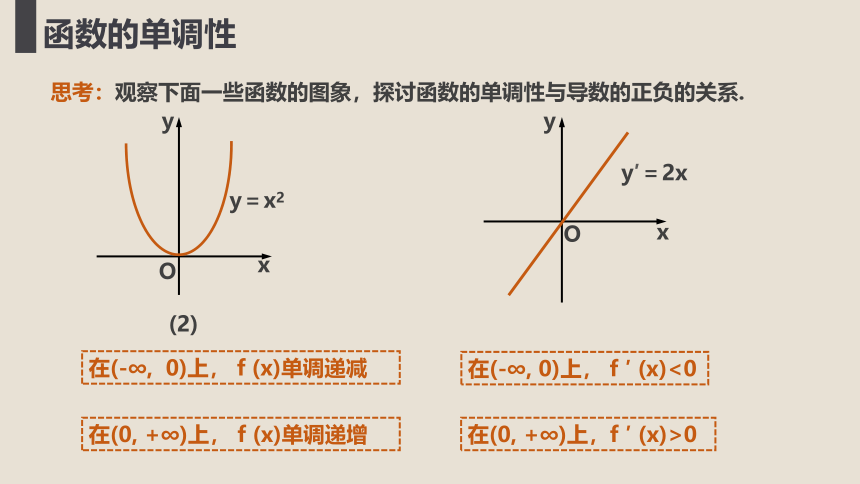
y=x2
(2)
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
x
y
O
y′=2x
函数的单调性
思考:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
x
y
O
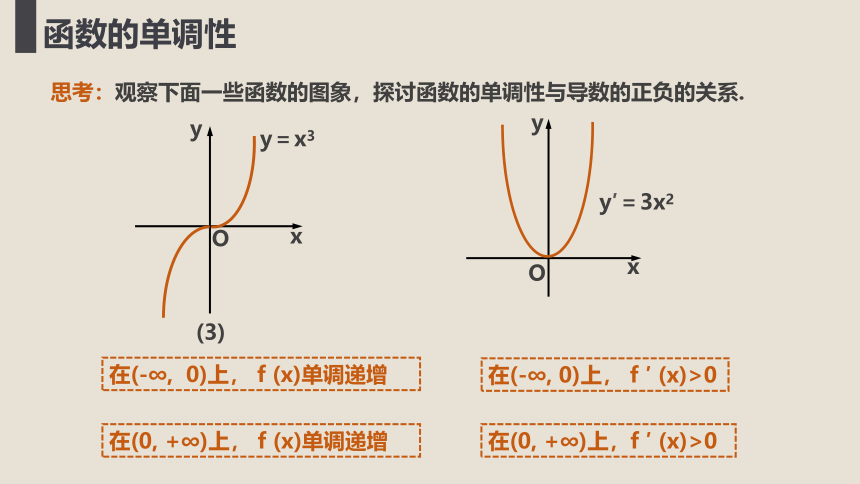
y=x3
(3)
在(-∞, 0)上, f (x)单调递增
在(-∞, 0)上, f ′ (x)>0
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
x
y
O
y′=3x2
函数的单调性
思考:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
x
y
O
(4)
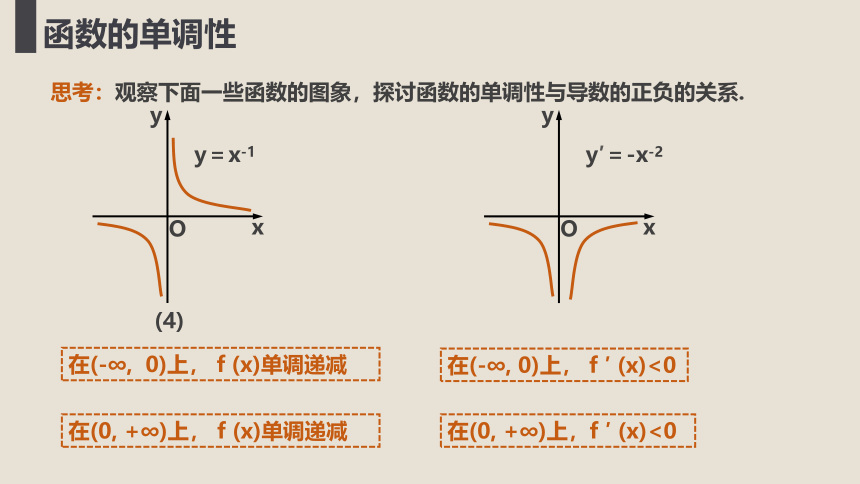
y=x-1
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
在(0, +∞)上, f (x)单调递减
在(0, +∞)上,f ′ (x)<0
x
y
O
y′=-x-2
函数的单调性与导数的正负的关系
如图示,导数f'(x0)表示函数y=f(x)的图象在点(x0, f(x0))处的切线的斜率,
可以发现:
在x=x0处,f'(x0)>0,切线是“左下右上”的上升式,
函数f(x)的图象也是上升的,
函数f(x)在x=x0附近单调递增;
在x=x1处,f'(x1)<0,切线是“左上右下”的下降式,
函数f(x)的图象也是下降的,
函数f(x)在x=x1附近单调递减.
x
y
O
(x0, f(x0))
(x1, f(x1))
函数的单调性与导数的正负的关系
一般地,函数f (x)的单调性与导函数f ′(x)的正负之间具有如下的关系:
在某个区间(a,b)上,如果f ′(x)>0 ,那么函数y=f (x)在区间(a,b)上单调递增;
在某个区间(a,b)上,如果f ′(x)<0 ,那么函数y=f (x)在区间(a,b)上单调递减.
思考:如果在某个区间上恒有f ′(x)=0,那么函数f (x)有什么特性?
在某个区间上恒有f′(x)=0,那么函数y=f(x)在这个区间内是常函数.
注意:若在某区间上有有限个点使f′(x)=0,在其余的点恒有f′(x)>0,
则f(x)仍为增函数(减函数的情形完全类似)。
函数与导函数图象的关系
C
利用导数判断函数的单调性
典例2:利用导数判断下列函数的单调性
x
y
O
(1)
x
y
O
(2)
π
-π
利用导数判断函数的单调性
x
y
O
(3)
1
1
判定函数单调性的步骤:
① 求出函数的定义域;
② 求出函数的导数f (x);
③ 判定导数f (x)的符号;
④ 确定函数f(x)的单调性.
RART 03
典型例题
利用导数判断不含参函数的单调性
例1:求下列函数的单调区间
利用导数判断不含参函数的单调性
例1:求下列函数的单调区间
利用导数判断不含参函数的单调性
例1:求下列函数的单调区间
利用导数判断含参函数的单调性
利用导数判断含参函数的单调性
利用导数判断含参函数的单调性
已知函数单调性求参数范围
函数的单调性 导数
单调递增 f′(x)≥0且f′(x)不恒为0
单调递减 f′(x)≤0且f′(x)不恒为0
常函数 f′(x)=0
已知函数单调性求参数范围
已知函数单调性求参数范围
由函数的单调性求参数取值范围的方法技巧
已知函数单调性求参数范围
RART 04
课堂总结
课堂总结
1.函数的单调性;
2.函数的单调性与导数正负的关系;
3.利用导数判断函数的单调性;
4根据函数单调性求参数范围。
感谢您的观看
2022
我们必须知道,我们必将知道 --希尔伯特
第五章一元函数的导数及其应用
5.3.1函数的单调性(第一课时)
李思
2022
目录
CONTENTS
知识回顾
课堂总结
典型例题
函数的单调性
01
02
03
04
RART 01
知识回顾
知识回顾
1.函数单调性的定义是什么?
对于给定区间D上的函数f(x),若对于属于区间D的任意两个自变量的值x1,x2,
当x1
在必修第一册中, 我们通过图象直观,利用不等式、方程等知识,研究了函数的单调性、周期性、奇偶性以及最大(小)值等性质.
在本章前两节中,我们学习了导数的概念和运算,知道导数定量地刻画了函数的局部变化. 能否利用导数更加精确地研究函数的性质呢 本节我们就来讨论这个问题.
RART 02
函数的单调性与导数
函数的单调性
思考:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
x
y
O
y=x
(1)
x
y
O
y=x2
(2)
x
y
O
y=x3
(3)
x
y
O
(4)
y=x-1
函数的单调性
思考:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
x
y
O
y=x
(1)
在(-∞, +∞)上, f (x)单调递增
在(-∞, +∞)上,f ′ (x)>0
x
y
O
y′=1
函数的单调性
思考:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
x
y
O
y=x2
(2)
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
x
y
O
y′=2x
函数的单调性
思考:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
x
y
O
y=x3
(3)
在(-∞, 0)上, f (x)单调递增
在(-∞, 0)上, f ′ (x)>0
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
x
y
O
y′=3x2
函数的单调性
思考:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
x
y
O
(4)
y=x-1
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
在(0, +∞)上, f (x)单调递减
在(0, +∞)上,f ′ (x)<0
x
y
O
y′=-x-2
函数的单调性与导数的正负的关系
如图示,导数f'(x0)表示函数y=f(x)的图象在点(x0, f(x0))处的切线的斜率,
可以发现:
在x=x0处,f'(x0)>0,切线是“左下右上”的上升式,
函数f(x)的图象也是上升的,
函数f(x)在x=x0附近单调递增;
在x=x1处,f'(x1)<0,切线是“左上右下”的下降式,
函数f(x)的图象也是下降的,
函数f(x)在x=x1附近单调递减.
x
y
O
(x0, f(x0))
(x1, f(x1))
函数的单调性与导数的正负的关系
一般地,函数f (x)的单调性与导函数f ′(x)的正负之间具有如下的关系:
在某个区间(a,b)上,如果f ′(x)>0 ,那么函数y=f (x)在区间(a,b)上单调递增;
在某个区间(a,b)上,如果f ′(x)<0 ,那么函数y=f (x)在区间(a,b)上单调递减.
思考:如果在某个区间上恒有f ′(x)=0,那么函数f (x)有什么特性?
在某个区间上恒有f′(x)=0,那么函数y=f(x)在这个区间内是常函数.
注意:若在某区间上有有限个点使f′(x)=0,在其余的点恒有f′(x)>0,
则f(x)仍为增函数(减函数的情形完全类似)。
函数与导函数图象的关系
C
利用导数判断函数的单调性
典例2:利用导数判断下列函数的单调性
x
y
O
(1)
x
y
O
(2)
π
-π
利用导数判断函数的单调性
x
y
O
(3)
1
1
判定函数单调性的步骤:
① 求出函数的定义域;
② 求出函数的导数f (x);
③ 判定导数f (x)的符号;
④ 确定函数f(x)的单调性.
RART 03
典型例题
利用导数判断不含参函数的单调性
例1:求下列函数的单调区间
利用导数判断不含参函数的单调性
例1:求下列函数的单调区间
利用导数判断不含参函数的单调性
例1:求下列函数的单调区间
利用导数判断含参函数的单调性
利用导数判断含参函数的单调性
利用导数判断含参函数的单调性
已知函数单调性求参数范围
函数的单调性 导数
单调递增 f′(x)≥0且f′(x)不恒为0
单调递减 f′(x)≤0且f′(x)不恒为0
常函数 f′(x)=0
已知函数单调性求参数范围
已知函数单调性求参数范围
由函数的单调性求参数取值范围的方法技巧
已知函数单调性求参数范围
RART 04
课堂总结
课堂总结
1.函数的单调性;
2.函数的单调性与导数正负的关系;
3.利用导数判断函数的单调性;
4根据函数单调性求参数范围。
感谢您的观看
2022
我们必须知道,我们必将知道 --希尔伯特
