第7章数据的收集、整理、描述 单元测试题 (含解析) 2022-2023学年苏科版八年级数学下册
文档属性
| 名称 | 第7章数据的收集、整理、描述 单元测试题 (含解析) 2022-2023学年苏科版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 898.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 11:30:59 | ||
图片预览



文档简介
2022-2023学年苏科版八年级数学下册《第7章数据的收集、整理、描述》
单元综合测试题(附答案)
一.选择题(共7小题,满分35分)
1.下列问题中,最适合采用全面调查(普查)方式的是( )
A.调查一批灯泡的使用寿命
B.调查一架“歼20”飞机各零部件的质量
C.调查全国中学生对“天宫课堂”的了解情况
D.调查某市空气质量情况
2.为了解我市参加中考的5000名学生的身高情况,抽查了其中200名学生的身高进行统计分析.下列叙述正确的是( )
A.5000名学生是总体 B.从中抽取的200名学生的身高是总体的一个样本 C.每名学生是总体的一个个体 D.以上调查是全面调查
3.要了解某小区老年人的健康状况,下面是小明、小颖、小亮三个小组的调查结果:
小明:“我们小组在公园随机调查了100名健身的老年人的健康状况”;
小颖:“我们小组去医院随机调查了100名老年人的健康状况”;
小亮:“我们小组在小区内随机询问了100名老年人的健康状况”.
他们三个小组的调查结果,更可靠的是( )
A.小明 B.小颖 C.小亮 D.都可靠
4.为了清楚地表示学校各年级学生占全校学生总人数的百分比,应绘制( )统计图.
A.条形 B.折线 C.扇形 D.复合
5.下列实数,3.14中,无理数出现的频率为( )
A.20% B.40% C.60% D.80%
6.某班对学生的一次数学测试成绩(得分取整数)进行整理后分成五组,并绘制出如图所示的频数分布直方图,则下列说法中错误的是( )
A.这次共有48人参加测试 B.这次成绩为100分的有6人
C.测试成绩高于70.5分且低于80.5分的人数最多
D.若成绩在80分以上为优秀,则成绩为优秀的有15人
7.如图所示是甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年教费用判断正确的是( )
A.甲户比乙户多 B.乙户比甲户多
C.甲、乙两户一样多 D.无法确定哪一户多
二.填空题(共7小题,满分35分)
8.为了调查电视机的使用寿命,从一批电视机中抽取20台进行测试,这个问题中,样本是 ,样本容量是 .
9.在2.10500500051中,“0”出现的频率为 .
10.在一个不透明的盒子里仅有白球若干个,为了知道这些白球的个数,小明同学往盒子里放了10个除颜色外其它都与原白球相同的红球,摇匀后随机抽取了8个球,其中有2个红球,则盒子中约有白球 个.
11.火箭发射前科学工作者要对神舟飞船进行检查,检查的方式是 (填“全面调查”或“抽样调查”).
12.一次数学测试后,某班50名学生的成绩被分为5组,第1~4组的频数分别为12,10,8,8,则第5组的学生人数占全班的百分比是 .
13.如图反映的是双十中学七(3)班学生外出方式(乘车、步行、骑车)人数的条形统计图(部分)和扇形分布图,那么扇形图中骑车的学生人数所占的圆心角是 °.
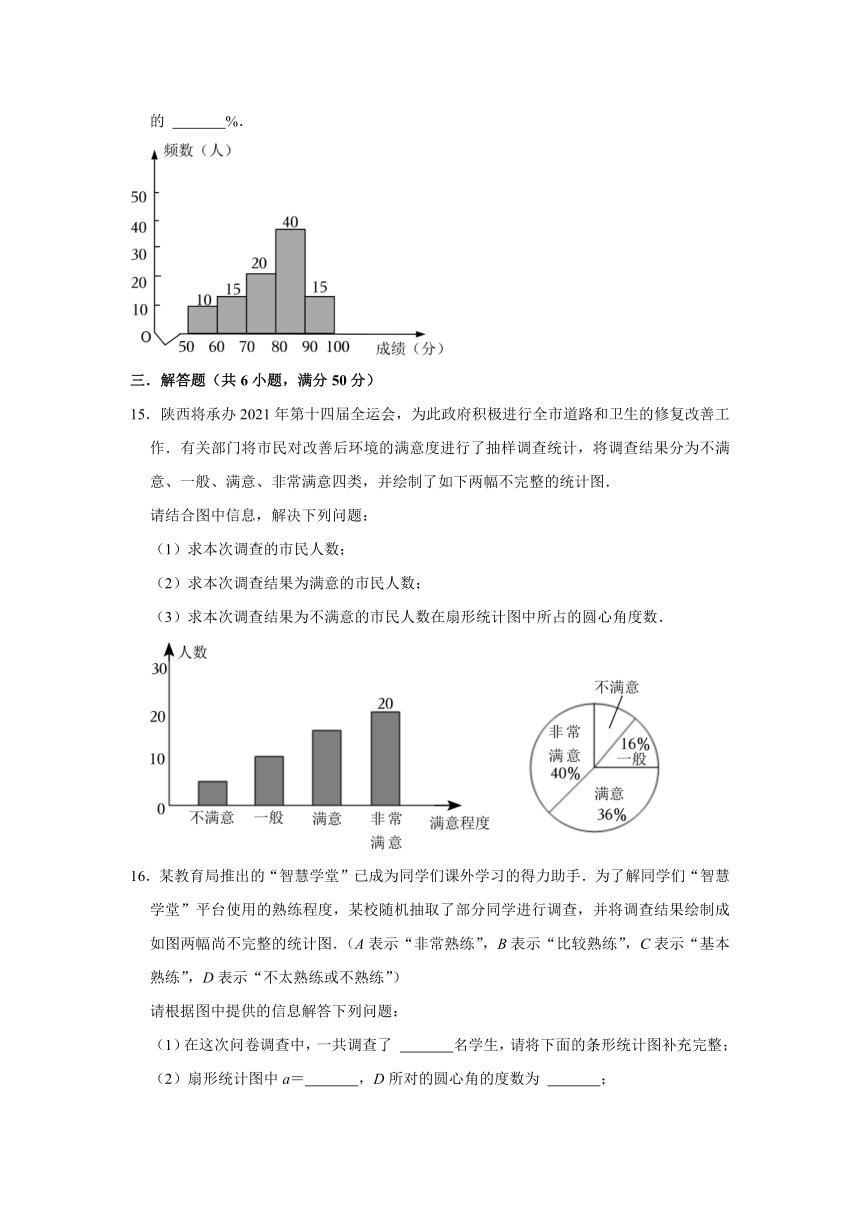
14.为了庆祝中国共产党建党100周年,某中学举办了党史知识大赛,赛后随机抽取了部分试卷进行调查,整理并绘制成如下频数分布直方图(每组含前一个数,不含后一个数).若比赛成绩大于等于90分为优秀,则本次调查成绩为优秀的学生占调查总人数的 %.
三.解答题(共6小题,满分50分)
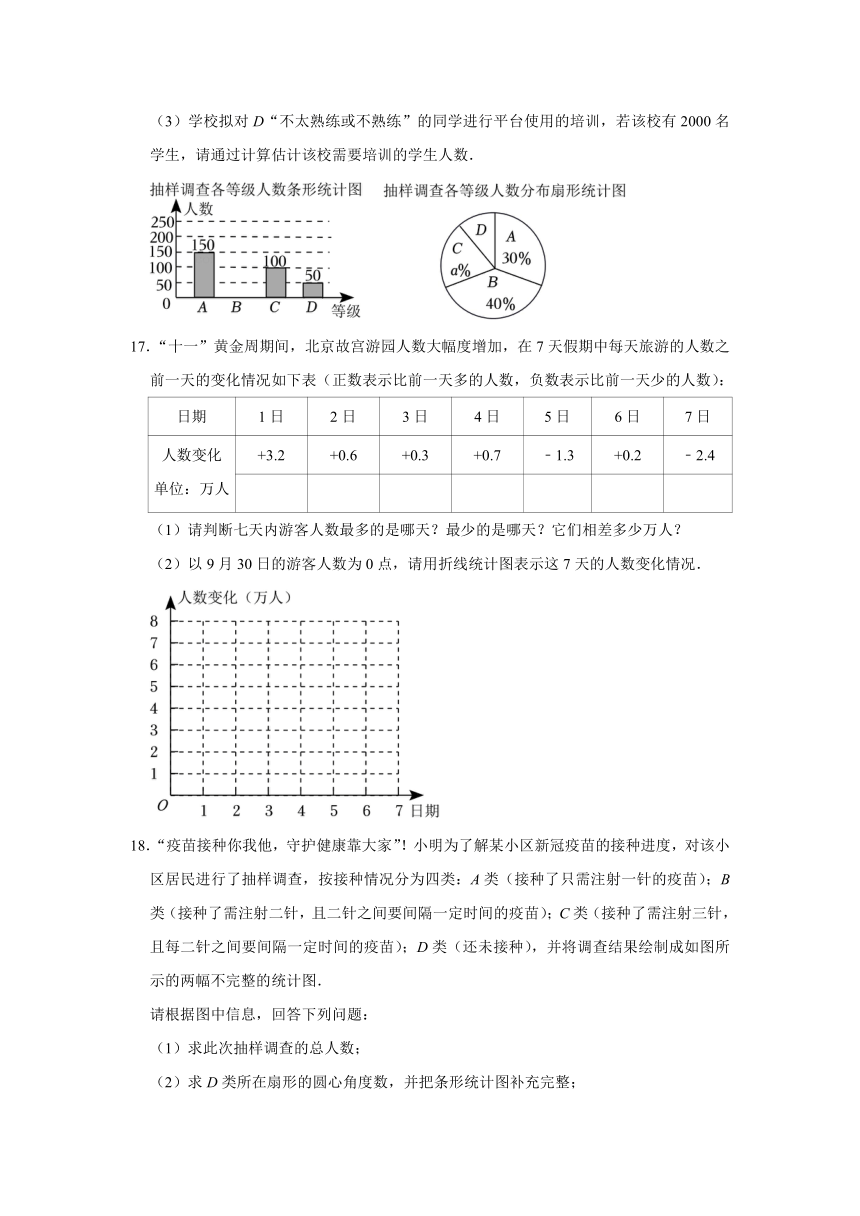
15.陕西将承办2021年第十四届全运会,为此政府积极进行全市道路和卫生的修复改善工作.有关部门将市民对改善后环境的满意度进行了抽样调查统计,将调查结果分为不满意、一般、满意、非常满意四类,并绘制了如下两幅不完整的统计图.
请结合图中信息,解决下列问题:
(1)求本次调查的市民人数;
(2)求本次调查结果为满意的市民人数;
(3)求本次调查结果为不满意的市民人数在扇形统计图中所占的圆心角度数.
16.某教育局推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如图两幅尚不完整的统计图.(A表示“非常熟练”,B表示“比较熟练”,C表示“基本熟练”,D表示“不太熟练或不熟练”)
请根据图中提供的信息解答下列问题:
(1)在这次问卷调查中,一共调查了 名学生,请将下面的条形统计图补充完整;
(2)扇形统计图中a= ,D所对的圆心角的度数为 ;
(3)学校拟对D“不太熟练或不熟练”的同学进行平台使用的培训,若该校有2000名学生,请通过计算估计该校需要培训的学生人数.
17.“十一”黄金周期间,北京故宫游园人数大幅度增加,在7天假期中每天旅游的人数之前一天的变化情况如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 1日 2日 3日 4日 5日 6日 7日
人数变化 单位:万人 +3.2 +0.6 +0.3 +0.7 ﹣1.3 +0.2 ﹣2.4
(1)请判断七天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(2)以9月30日的游客人数为0点,请用折线统计图表示这7天的人数变化情况.
18.“疫苗接种你我他,守护健康靠大家”!小明为了解某小区新冠疫苗的接种进度,对该小区居民进行了抽样调查,按接种情况分为四类:A类(接种了只需注射一针的疫苗);B类(接种了需注射二针,且二针之间要间隔一定时间的疫苗);C类(接种了需注射三针,且每二针之间要间隔一定时间的疫苗);D类(还未接种),并将调查结果绘制成如图所示的两幅不完整的统计图.
请根据图中信息,回答下列问题:
(1)求此次抽样调查的总人数;
(2)求D类所在扇形的圆心角度数,并把条形统计图补充完整;
(3)若该小区现有居民8000名,求接种B类新冠疫苗的人数.
19.在“双减”背景下,某校拟开展课后服务活动,对各班同学的业余兴趣爱好进行了一次调查,根据采集到某班的数据绘制了下面的统计图.请据图中提供的信息,解答下列问题:
(1)该班共有 人;
(2)在图1中,请将条形统计图补充完整;
(3)在图2的扇形统计图中,求音乐部分所对应的圆心角的度数.
20.戏曲进校园.某校随机抽取七年级部分学生,对他们是否了解关于“宿州梆子戏”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.根据调查的数据进行整理,绘制了尚不完整的统计图如图,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题:
(1)求本次活动共调查了 名学生;图1中,B区域的圆心角度是 ;
(2)补全条形统计图.
(3)若该校七年级有1200名学生,请估算该校不是“了解很多”的学生人数.
参考答案
一.选择题(共7小题,满分35分)
1.解:A.调查一批灯泡的使用寿命,适合使用抽样调查,因此选项A不符合题意;
B.调查一架“歼20”飞机各零部件的质量,适合使用全面调查,因此选项B符合题意;
C.调查全国中学生对“天宫课堂”的了解情况,适合使用抽样调查,因此选项C不符合题意;
D.调查某市空气质量情况,适合使用抽样调查,因此选项D不符合题意;
故选:B.
2.解:A.5000名学生的身高情况是总体,故本选项不合题意;
B.从中抽取的200名学生的身高是总体的一个样本,故本选项符合题意;
C.每名学生的身高情况是总体的一个个体,故本选项不合题意;
D.该调查是抽样调查,故本选项不合题意;
故选:B.
3.解:为确保抽取的样本的广泛性、代表性和可靠性可知,小亮的做法较好,
故选:C.
4.解:为了清楚地表示学校各年级学生占全校学生总人数的百分比,应绘制扇形统计图.
故选:C.
5.解:无理数有,π,,共3个,
故无理数的频率为:×100%=60%.
故选:C.
6.解:A、这次活动共抽调了3+12+18+9+6=48人测试,此选项不符合题意;
B、由图可知90.5~100.5组的有6人,不一定都是100分,此选项符合题意;
C、测试成绩在70﹣80分的人数为18人,最多,此选项不符合题意;
D、测试成绩在80分以上的人数为15人,此选项不符合题意;
故选:B.
7.解:因为两个扇形统计图的总体都不明确,
所以A、B、C都错误,
故选:D.
二.填空题(共7小题,满分35分)
8.解:为了调查电视机的使用寿命,从一批电视机中抽取20台进行测试,这个问题中,样本是是抽取20台电视机的使用寿命,样本容量是20,
故答案为:抽取20台电视机的使用寿命;20.
9.解:6÷12=0.5,
故答案为:0.5.
10.解:∵随机抽取了8个球,其中有2个红球,
∴红球所占的概率为,
又∵盒子里共有10个红球,
∴盒子里的总球数约为:(个),
∴盒子中白球数量约为:40﹣10=30(个).
故答案为:30.
11.解:火箭发射前科学工作者要对神舟飞船进行检查,检查的方式是全面调查.
故答案为:全面调查.
12.解:由题意得,第5组的频数为50﹣12﹣10﹣8﹣8=12,
∴第5组的学生人数占全班的百分比是.
故答案为:24%.
13.解:根据频数分布直方图可知,乘车的学生人数为20人,骑车学生人数为12人,
根据扇形统计图可知,乘车人数所占百分比为50%,
总人数为:20÷50%=40人,
骑车的学生人数所占百分比为:,
扇形图中骑车的学生人数所占的圆心角为:360°×30%=108°.
故答案为:108.
14.解:由题意可知,本次调查成绩为优秀的学生占调查总人数百分比为:
=15%.
故答案为:15.
三.解答题(共6小题,满分50分)
15.解:(1)20÷40%=50(人),
即本次调查的市民有50人;
(2)50×36%=18(人),
即本次调查结果为满意的市民有18人;
(3)360°×(1﹣40%﹣36%﹣16%)
=360°×8%
=28.8°,
即本次调查结果为不满意的市民人数在扇形统计图中所占的圆心角度数是28.8°.
16.解:(1)条形统计图中A等级的人数为150,扇形统计图中A等级所占比例为30%,
∴本次调查的样本容量为150÷30%=500,
∴B等级人数为:500×40%=200(人),
补全条形统计图如下:
故答案为:500;
(2)扇形统计图中a==20,D所对的圆心角的度数为:360°×(1﹣20%﹣30%﹣40%)=36°.
故答案为:20;36°;
(3)∵本次调查的样本容量为500,D等级人数为50人,
∴D等级人数所占比例为×100%=10%,
∴全校2000人需要培训的学生人数2000×10%=200(人),
故估计该校需要培训的学生人数为200人.
17.解:(1)∵3.2+0.6+0.3+0.7=4.8(万人),
∴4日游客最多,
∵4.8﹣1.3=3.5(万元),3.5+0.2=3.7(万元),3.7﹣2.4=1.3(万人),
∴7日游客最少,
∵4.8﹣1.3=3.5(万人),
∴最多与最少那天相差3.5万人;
(2)如图所示.
18.解:(1)此次抽样调查的总人数为:100÷50%=200(人);
(2)D等级所在扇形的圆心角度数:×360°=18°,
B类的人数有:200﹣30﹣10﹣100=60(人),
补全统计图如图所示:
(3)接种B类新冠疫苗的人数为:60÷200×8000=2400(人).
19.解:(1)该班共有的人数有:16÷32%=50(人),
故答案为:50;
(2)选择书画的人数为:50﹣(16+14+6)=14(人),
补全统计图如下:
(3)音乐部分所对应的圆心角的度数为:360°×=100.8°.
20.解:(1)本次活动共调查了:20÷=200(名)学生,
B区域的圆心角度是:360°×=108°,
故答案为:200,108°.
(2)调查结果为B的学生有:200﹣120﹣20=60(人).
补全的条形统计图如右图所示;
(3)1200×=480(人),
即估算该校不是“了解很多”的学生有480人.
单元综合测试题(附答案)
一.选择题(共7小题,满分35分)
1.下列问题中,最适合采用全面调查(普查)方式的是( )
A.调查一批灯泡的使用寿命
B.调查一架“歼20”飞机各零部件的质量
C.调查全国中学生对“天宫课堂”的了解情况
D.调查某市空气质量情况
2.为了解我市参加中考的5000名学生的身高情况,抽查了其中200名学生的身高进行统计分析.下列叙述正确的是( )
A.5000名学生是总体 B.从中抽取的200名学生的身高是总体的一个样本 C.每名学生是总体的一个个体 D.以上调查是全面调查
3.要了解某小区老年人的健康状况,下面是小明、小颖、小亮三个小组的调查结果:
小明:“我们小组在公园随机调查了100名健身的老年人的健康状况”;
小颖:“我们小组去医院随机调查了100名老年人的健康状况”;
小亮:“我们小组在小区内随机询问了100名老年人的健康状况”.
他们三个小组的调查结果,更可靠的是( )
A.小明 B.小颖 C.小亮 D.都可靠
4.为了清楚地表示学校各年级学生占全校学生总人数的百分比,应绘制( )统计图.
A.条形 B.折线 C.扇形 D.复合
5.下列实数,3.14中,无理数出现的频率为( )
A.20% B.40% C.60% D.80%
6.某班对学生的一次数学测试成绩(得分取整数)进行整理后分成五组,并绘制出如图所示的频数分布直方图,则下列说法中错误的是( )
A.这次共有48人参加测试 B.这次成绩为100分的有6人
C.测试成绩高于70.5分且低于80.5分的人数最多
D.若成绩在80分以上为优秀,则成绩为优秀的有15人
7.如图所示是甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年教费用判断正确的是( )
A.甲户比乙户多 B.乙户比甲户多
C.甲、乙两户一样多 D.无法确定哪一户多
二.填空题(共7小题,满分35分)
8.为了调查电视机的使用寿命,从一批电视机中抽取20台进行测试,这个问题中,样本是 ,样本容量是 .
9.在2.10500500051中,“0”出现的频率为 .
10.在一个不透明的盒子里仅有白球若干个,为了知道这些白球的个数,小明同学往盒子里放了10个除颜色外其它都与原白球相同的红球,摇匀后随机抽取了8个球,其中有2个红球,则盒子中约有白球 个.
11.火箭发射前科学工作者要对神舟飞船进行检查,检查的方式是 (填“全面调查”或“抽样调查”).
12.一次数学测试后,某班50名学生的成绩被分为5组,第1~4组的频数分别为12,10,8,8,则第5组的学生人数占全班的百分比是 .
13.如图反映的是双十中学七(3)班学生外出方式(乘车、步行、骑车)人数的条形统计图(部分)和扇形分布图,那么扇形图中骑车的学生人数所占的圆心角是 °.
14.为了庆祝中国共产党建党100周年,某中学举办了党史知识大赛,赛后随机抽取了部分试卷进行调查,整理并绘制成如下频数分布直方图(每组含前一个数,不含后一个数).若比赛成绩大于等于90分为优秀,则本次调查成绩为优秀的学生占调查总人数的 %.
三.解答题(共6小题,满分50分)
15.陕西将承办2021年第十四届全运会,为此政府积极进行全市道路和卫生的修复改善工作.有关部门将市民对改善后环境的满意度进行了抽样调查统计,将调查结果分为不满意、一般、满意、非常满意四类,并绘制了如下两幅不完整的统计图.
请结合图中信息,解决下列问题:
(1)求本次调查的市民人数;
(2)求本次调查结果为满意的市民人数;
(3)求本次调查结果为不满意的市民人数在扇形统计图中所占的圆心角度数.
16.某教育局推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如图两幅尚不完整的统计图.(A表示“非常熟练”,B表示“比较熟练”,C表示“基本熟练”,D表示“不太熟练或不熟练”)
请根据图中提供的信息解答下列问题:
(1)在这次问卷调查中,一共调查了 名学生,请将下面的条形统计图补充完整;
(2)扇形统计图中a= ,D所对的圆心角的度数为 ;
(3)学校拟对D“不太熟练或不熟练”的同学进行平台使用的培训,若该校有2000名学生,请通过计算估计该校需要培训的学生人数.
17.“十一”黄金周期间,北京故宫游园人数大幅度增加,在7天假期中每天旅游的人数之前一天的变化情况如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 1日 2日 3日 4日 5日 6日 7日
人数变化 单位:万人 +3.2 +0.6 +0.3 +0.7 ﹣1.3 +0.2 ﹣2.4
(1)请判断七天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(2)以9月30日的游客人数为0点,请用折线统计图表示这7天的人数变化情况.
18.“疫苗接种你我他,守护健康靠大家”!小明为了解某小区新冠疫苗的接种进度,对该小区居民进行了抽样调查,按接种情况分为四类:A类(接种了只需注射一针的疫苗);B类(接种了需注射二针,且二针之间要间隔一定时间的疫苗);C类(接种了需注射三针,且每二针之间要间隔一定时间的疫苗);D类(还未接种),并将调查结果绘制成如图所示的两幅不完整的统计图.
请根据图中信息,回答下列问题:
(1)求此次抽样调查的总人数;
(2)求D类所在扇形的圆心角度数,并把条形统计图补充完整;
(3)若该小区现有居民8000名,求接种B类新冠疫苗的人数.
19.在“双减”背景下,某校拟开展课后服务活动,对各班同学的业余兴趣爱好进行了一次调查,根据采集到某班的数据绘制了下面的统计图.请据图中提供的信息,解答下列问题:
(1)该班共有 人;
(2)在图1中,请将条形统计图补充完整;
(3)在图2的扇形统计图中,求音乐部分所对应的圆心角的度数.
20.戏曲进校园.某校随机抽取七年级部分学生,对他们是否了解关于“宿州梆子戏”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.根据调查的数据进行整理,绘制了尚不完整的统计图如图,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题:
(1)求本次活动共调查了 名学生;图1中,B区域的圆心角度是 ;
(2)补全条形统计图.
(3)若该校七年级有1200名学生,请估算该校不是“了解很多”的学生人数.
参考答案
一.选择题(共7小题,满分35分)
1.解:A.调查一批灯泡的使用寿命,适合使用抽样调查,因此选项A不符合题意;
B.调查一架“歼20”飞机各零部件的质量,适合使用全面调查,因此选项B符合题意;
C.调查全国中学生对“天宫课堂”的了解情况,适合使用抽样调查,因此选项C不符合题意;
D.调查某市空气质量情况,适合使用抽样调查,因此选项D不符合题意;
故选:B.
2.解:A.5000名学生的身高情况是总体,故本选项不合题意;
B.从中抽取的200名学生的身高是总体的一个样本,故本选项符合题意;
C.每名学生的身高情况是总体的一个个体,故本选项不合题意;
D.该调查是抽样调查,故本选项不合题意;
故选:B.
3.解:为确保抽取的样本的广泛性、代表性和可靠性可知,小亮的做法较好,
故选:C.
4.解:为了清楚地表示学校各年级学生占全校学生总人数的百分比,应绘制扇形统计图.
故选:C.
5.解:无理数有,π,,共3个,
故无理数的频率为:×100%=60%.
故选:C.
6.解:A、这次活动共抽调了3+12+18+9+6=48人测试,此选项不符合题意;
B、由图可知90.5~100.5组的有6人,不一定都是100分,此选项符合题意;
C、测试成绩在70﹣80分的人数为18人,最多,此选项不符合题意;
D、测试成绩在80分以上的人数为15人,此选项不符合题意;
故选:B.
7.解:因为两个扇形统计图的总体都不明确,
所以A、B、C都错误,
故选:D.
二.填空题(共7小题,满分35分)
8.解:为了调查电视机的使用寿命,从一批电视机中抽取20台进行测试,这个问题中,样本是是抽取20台电视机的使用寿命,样本容量是20,
故答案为:抽取20台电视机的使用寿命;20.
9.解:6÷12=0.5,
故答案为:0.5.
10.解:∵随机抽取了8个球,其中有2个红球,
∴红球所占的概率为,
又∵盒子里共有10个红球,
∴盒子里的总球数约为:(个),
∴盒子中白球数量约为:40﹣10=30(个).
故答案为:30.
11.解:火箭发射前科学工作者要对神舟飞船进行检查,检查的方式是全面调查.
故答案为:全面调查.
12.解:由题意得,第5组的频数为50﹣12﹣10﹣8﹣8=12,
∴第5组的学生人数占全班的百分比是.
故答案为:24%.
13.解:根据频数分布直方图可知,乘车的学生人数为20人,骑车学生人数为12人,
根据扇形统计图可知,乘车人数所占百分比为50%,
总人数为:20÷50%=40人,
骑车的学生人数所占百分比为:,
扇形图中骑车的学生人数所占的圆心角为:360°×30%=108°.
故答案为:108.
14.解:由题意可知,本次调查成绩为优秀的学生占调查总人数百分比为:
=15%.
故答案为:15.
三.解答题(共6小题,满分50分)
15.解:(1)20÷40%=50(人),
即本次调查的市民有50人;
(2)50×36%=18(人),
即本次调查结果为满意的市民有18人;
(3)360°×(1﹣40%﹣36%﹣16%)
=360°×8%
=28.8°,
即本次调查结果为不满意的市民人数在扇形统计图中所占的圆心角度数是28.8°.
16.解:(1)条形统计图中A等级的人数为150,扇形统计图中A等级所占比例为30%,
∴本次调查的样本容量为150÷30%=500,
∴B等级人数为:500×40%=200(人),
补全条形统计图如下:
故答案为:500;
(2)扇形统计图中a==20,D所对的圆心角的度数为:360°×(1﹣20%﹣30%﹣40%)=36°.
故答案为:20;36°;
(3)∵本次调查的样本容量为500,D等级人数为50人,
∴D等级人数所占比例为×100%=10%,
∴全校2000人需要培训的学生人数2000×10%=200(人),
故估计该校需要培训的学生人数为200人.
17.解:(1)∵3.2+0.6+0.3+0.7=4.8(万人),
∴4日游客最多,
∵4.8﹣1.3=3.5(万元),3.5+0.2=3.7(万元),3.7﹣2.4=1.3(万人),
∴7日游客最少,
∵4.8﹣1.3=3.5(万人),
∴最多与最少那天相差3.5万人;
(2)如图所示.
18.解:(1)此次抽样调查的总人数为:100÷50%=200(人);
(2)D等级所在扇形的圆心角度数:×360°=18°,
B类的人数有:200﹣30﹣10﹣100=60(人),
补全统计图如图所示:
(3)接种B类新冠疫苗的人数为:60÷200×8000=2400(人).
19.解:(1)该班共有的人数有:16÷32%=50(人),
故答案为:50;
(2)选择书画的人数为:50﹣(16+14+6)=14(人),
补全统计图如下:
(3)音乐部分所对应的圆心角的度数为:360°×=100.8°.
20.解:(1)本次活动共调查了:20÷=200(名)学生,
B区域的圆心角度是:360°×=108°,
故答案为:200,108°.
(2)调查结果为B的学生有:200﹣120﹣20=60(人).
补全的条形统计图如右图所示;
(3)1200×=480(人),
即估算该校不是“了解很多”的学生有480人.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
