2022-2023学年九年级数学下册北师大版 2.2二次函数的图象与性质同步练习(含答案)
文档属性
| 名称 | 2022-2023学年九年级数学下册北师大版 2.2二次函数的图象与性质同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 180.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 11:34:23 | ||
图片预览

文档简介
2.2 二次函数的图象与性质
同步练习
一、单选题
1.下列关于二次函数的图像和性质的叙述中,正确的是( )
A.点在函数图像上 B.开口方向向上
C.对称轴是直线 D.与直线有两个交点
2.已知,,三点都在二次函数的图象上,则,,的大小关系为( )
A. B. C. D.
3.在平面直角坐标系中,将二次函数的图像向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )
A. B. C. D.
4.用配方法将二次函数化为的形式为( )
A. B. C. D.
5.点A(m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上.若y1<y2,则m的取值范围为( )
A. B. C. D.
6.抛物线y=x2+3上有两点A(x1,y1),B(x2,y2),若y1<y2,则下列结论正确的是( )
A.0≤x1<x2 B.x2<x1≤0
C.x2<x1≤0或0≤x1<x2 D.以上都不对
7.已知实数,满足,则的最大值为( )
A.10 B.22 C.34 D.142
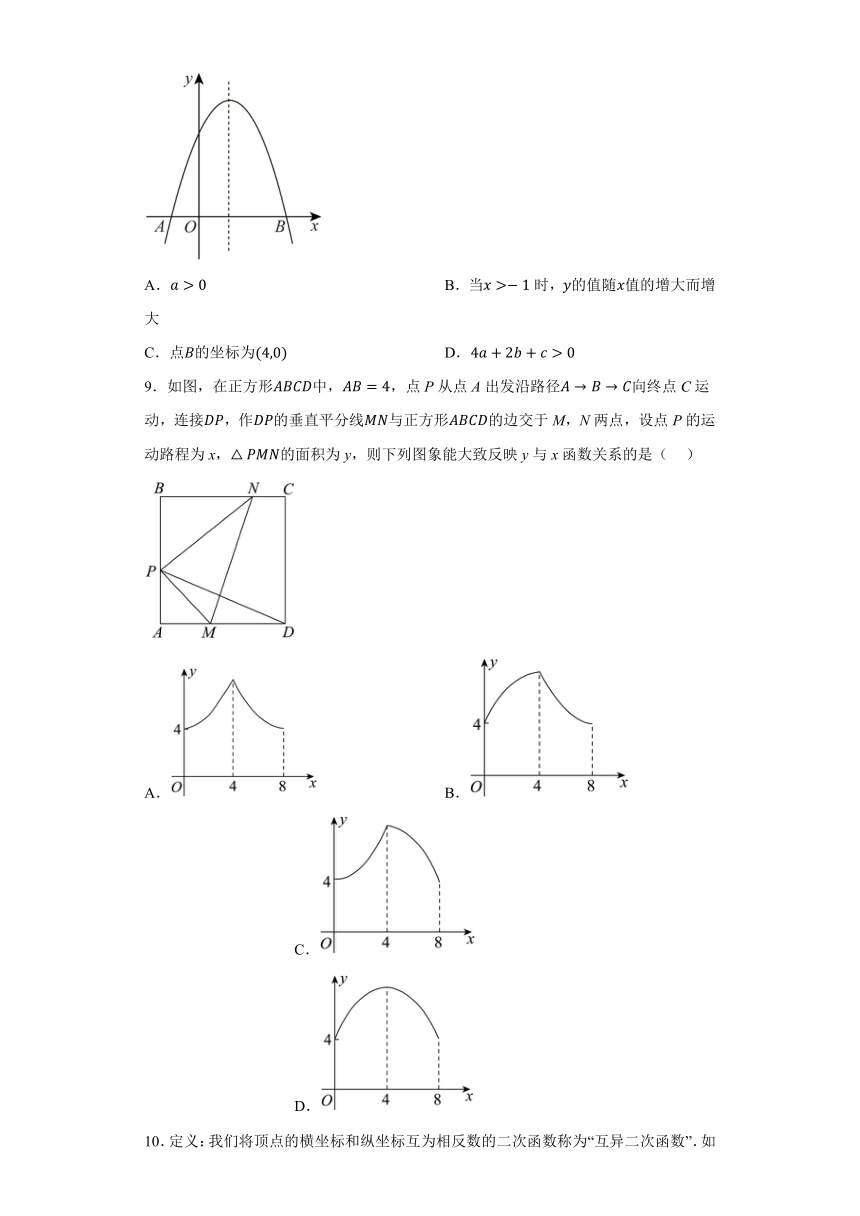
8.如图,二次函数的图像与轴相交于,两点,对称轴是直线,下列说法正确的是( )
A. B.当时,的值随值的增大而增大
C.点的坐标为 D.
9.如图,在正方形中,,点P从点A出发沿路径向终点C运动,连接,作的垂直平分线与正方形的边交于M,N两点,设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x函数关系的是( )
A. B. C. D.
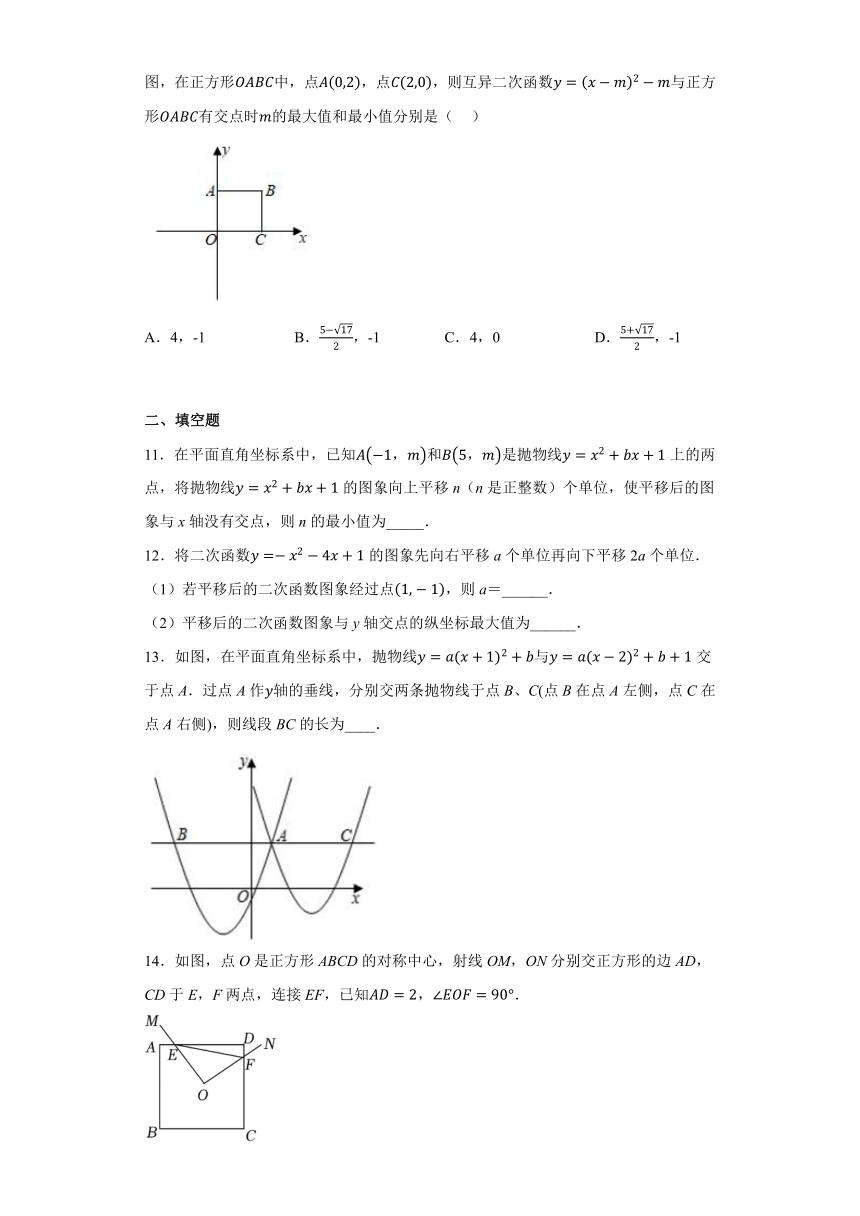
10.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形中,点,点,则互异二次函数与正方形有交点时的最大值和最小值分别是( )
A.4,-1 B.,-1 C.4,0 D.,-1
二、填空题
11.在平面直角坐标系中,已知和是抛物线上的两点,将抛物线的图象向上平移n(n是正整数)个单位,使平移后的图象与x轴没有交点,则n的最小值为_____.
12.将二次函数的图象先向右平移a个单位再向下平移2a个单位.
(1)若平移后的二次函数图象经过点,则a=______.
(2)平移后的二次函数图象与y轴交点的纵坐标最大值为______.
13.如图,在平面直角坐标系中,抛物线与交于点A.过点A作轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为____.
14.如图,点O是正方形ABCD的对称中心,射线OM,ON分别交正方形的边AD,CD于E,F两点,连接EF,已知,.
(1)以点E,O,F,D为顶点的图形的面积为_________;
(2)线段EF的最小值是_________.
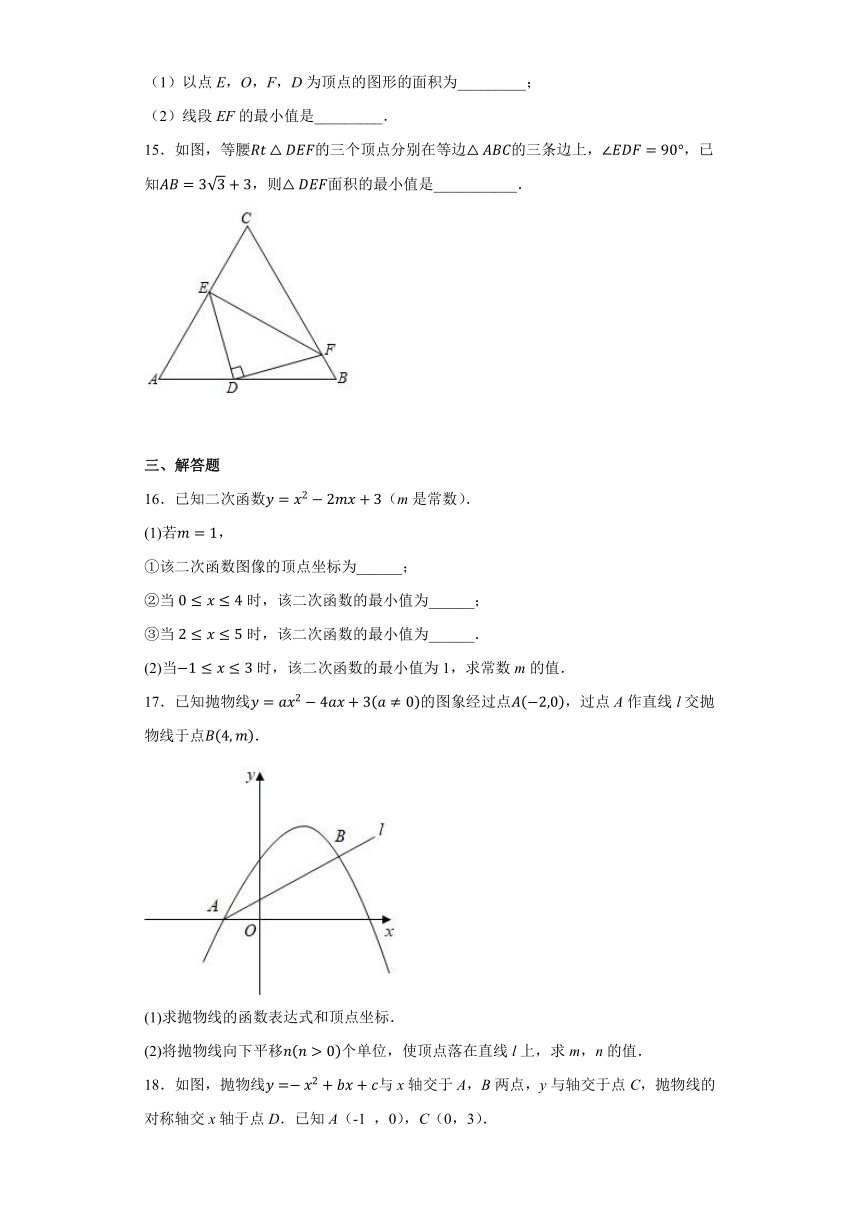
15.如图,等腰的三个顶点分别在等边的三条边上,,已知,则面积的最小值是___________.
三、解答题
16.已知二次函数(m是常数).
(1)若,
①该二次函数图像的顶点坐标为______;
②当时,该二次函数的最小值为______;
③当时,该二次函数的最小值为______.
(2)当时,该二次函数的最小值为1,求常数m的值.
17.已知抛物线的图象经过点,过点A作直线l交抛物线于点.
(1)求抛物线的函数表达式和顶点坐标.
(2)将抛物线向下平移个单位,使顶点落在直线l上,求m,n的值.
18.如图,抛物线与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1 ,0),C(0,3).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点M,使得MA+MC的值最小,求此点M的坐标;
(3)在抛物线的对称轴上是否存在P点,使△PCD是等腰三角形,如果存在,求出点P的坐标,如果不存在,请说明理由.
19.如图,已知抛物线y=x2﹣5x+4与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C.
(1)求A、B、C三点的坐标;
(2)如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ,当线段PQ长度最大时,判断四边形OCPQ的形状,并说明理由;
(3)如图2,在(2)的条件下,D是OC的中点,过点Q的直线与抛物线交于点E,且∠DQE=2∠ODQ.在y轴上是否存在点F,使得△BEF为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.
20.如图,点在抛物线C:上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为,.平移该胶片,使所在抛物线对应的函数恰为.求点移动的最短路程.
21.已知抛物线y=ax2 +bx+ l经过点(1,-2), (-2,13).
(1)求a,b的值;
(2)若(5,y1),(n,y2)是抛物线上不同的两点,且y2=12-y1,求n的值;
(3)将此抛物线沿x轴平移m(m>0)个单位长度,当自变量x的值满足-1≤x≤3时,与其对应的函数值y的最小值为6,求m的值.
参考答案:
1.D2.C3.B4.D5.B6.D7.C8.D9.A10.D
11.4
12. 3或1
13.6
14. 1
15.
16.(1)①;②2;③3
(2)或
17.(1);
(2)3;2
18.(1)
(2)点M坐标(1,2)
(3)存在,点P坐标为(1,6),(1,),(1,),(1,)
19.(1)解:对于y=x2﹣5x+4,令y=0,则0=x2﹣5x+4,
∴x1=4,x2=1,
∴点A(1,0),点B(4,0),
令x=0,则y=4,
∴点C(0,4);
(2)解:四边形OCPQ为平行四边形,理由如下:
∵点B的坐标为(4,0),点C(0,4),
设直线BC的表达式为y=kx+b,
则,
解得,
∴直线BC的表达式为y=﹣x+4,
设点P的坐标为(x,﹣x+4),则点Q的坐标为(x,x2﹣5x+4),
则PQ=(﹣x+4)﹣(x2﹣5x+4)=﹣x2+4x=﹣(x﹣2)2+4,
∵﹣1<0,
故PQ有最大值,
当x=2时,PQ的最大值为4=CO,
∴PQ=CO,PQOC,
∴四边形OCPQ为平行四边形;
(3)解:∵D是OC的中点,点C(0,4),
∴点D(0,2),
由(2)知:当x=2时,PQ的最大值为4,
当x=2时,y=x2﹣5x+4=﹣2,
∴Q(2,﹣2),
由点D、Q的坐标,同理可得,直线DQ的表达式为y=﹣2x+2,
过点Q作QH⊥x轴于点H,
则QHCO,故∠AQH=∠ODQ,
而∠DQE=2∠ODQ.
∴∠HQA=∠HQE,
则直线AQ和直线QE关于直线QH对称,
∴设直线QE的表达式为y=2x+r,
将点Q的坐标代入上式并解得r=﹣6,
∴直线QE的表达式为y=2x﹣6,
联立y=x2﹣5x+4得,
解得或(不合题意,舍去),
∴点E的坐标为(5,4),
设点F的坐标为(0,m),
∴BE2=(5﹣4)2+(4﹣0)2=17,
BF2=m2+42=m2+16,
EF2=(m﹣4)2+52,
当BE=BF时,即16+m2=17,解得m=±1;
当BE=EF时,即25+(m﹣4)2=17,方程无解;
当BF=EF时,即16+m2=25+(m﹣4)2,解得m= ;
故点F的坐标为(0,1)或(0,﹣1)或(0,).
20.(1)对称轴为直线,的最大值为4,
(2)5
21.(1)a=1,b=-4
(2)n的值为-1
(3)m的值为4或6
同步练习
一、单选题
1.下列关于二次函数的图像和性质的叙述中,正确的是( )
A.点在函数图像上 B.开口方向向上
C.对称轴是直线 D.与直线有两个交点
2.已知,,三点都在二次函数的图象上,则,,的大小关系为( )
A. B. C. D.
3.在平面直角坐标系中,将二次函数的图像向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )
A. B. C. D.
4.用配方法将二次函数化为的形式为( )
A. B. C. D.
5.点A(m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上.若y1<y2,则m的取值范围为( )
A. B. C. D.
6.抛物线y=x2+3上有两点A(x1,y1),B(x2,y2),若y1<y2,则下列结论正确的是( )
A.0≤x1<x2 B.x2<x1≤0
C.x2<x1≤0或0≤x1<x2 D.以上都不对
7.已知实数,满足,则的最大值为( )
A.10 B.22 C.34 D.142
8.如图,二次函数的图像与轴相交于,两点,对称轴是直线,下列说法正确的是( )
A. B.当时,的值随值的增大而增大
C.点的坐标为 D.
9.如图,在正方形中,,点P从点A出发沿路径向终点C运动,连接,作的垂直平分线与正方形的边交于M,N两点,设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x函数关系的是( )
A. B. C. D.
10.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形中,点,点,则互异二次函数与正方形有交点时的最大值和最小值分别是( )
A.4,-1 B.,-1 C.4,0 D.,-1
二、填空题
11.在平面直角坐标系中,已知和是抛物线上的两点,将抛物线的图象向上平移n(n是正整数)个单位,使平移后的图象与x轴没有交点,则n的最小值为_____.
12.将二次函数的图象先向右平移a个单位再向下平移2a个单位.
(1)若平移后的二次函数图象经过点,则a=______.
(2)平移后的二次函数图象与y轴交点的纵坐标最大值为______.
13.如图,在平面直角坐标系中,抛物线与交于点A.过点A作轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为____.
14.如图,点O是正方形ABCD的对称中心,射线OM,ON分别交正方形的边AD,CD于E,F两点,连接EF,已知,.
(1)以点E,O,F,D为顶点的图形的面积为_________;
(2)线段EF的最小值是_________.
15.如图,等腰的三个顶点分别在等边的三条边上,,已知,则面积的最小值是___________.
三、解答题
16.已知二次函数(m是常数).
(1)若,
①该二次函数图像的顶点坐标为______;
②当时,该二次函数的最小值为______;
③当时,该二次函数的最小值为______.
(2)当时,该二次函数的最小值为1,求常数m的值.
17.已知抛物线的图象经过点,过点A作直线l交抛物线于点.
(1)求抛物线的函数表达式和顶点坐标.
(2)将抛物线向下平移个单位,使顶点落在直线l上,求m,n的值.
18.如图,抛物线与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1 ,0),C(0,3).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点M,使得MA+MC的值最小,求此点M的坐标;
(3)在抛物线的对称轴上是否存在P点,使△PCD是等腰三角形,如果存在,求出点P的坐标,如果不存在,请说明理由.
19.如图,已知抛物线y=x2﹣5x+4与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C.
(1)求A、B、C三点的坐标;
(2)如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ,当线段PQ长度最大时,判断四边形OCPQ的形状,并说明理由;
(3)如图2,在(2)的条件下,D是OC的中点,过点Q的直线与抛物线交于点E,且∠DQE=2∠ODQ.在y轴上是否存在点F,使得△BEF为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.
20.如图,点在抛物线C:上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为,.平移该胶片,使所在抛物线对应的函数恰为.求点移动的最短路程.
21.已知抛物线y=ax2 +bx+ l经过点(1,-2), (-2,13).
(1)求a,b的值;
(2)若(5,y1),(n,y2)是抛物线上不同的两点,且y2=12-y1,求n的值;
(3)将此抛物线沿x轴平移m(m>0)个单位长度,当自变量x的值满足-1≤x≤3时,与其对应的函数值y的最小值为6,求m的值.
参考答案:
1.D2.C3.B4.D5.B6.D7.C8.D9.A10.D
11.4
12. 3或1
13.6
14. 1
15.
16.(1)①;②2;③3
(2)或
17.(1);
(2)3;2
18.(1)
(2)点M坐标(1,2)
(3)存在,点P坐标为(1,6),(1,),(1,),(1,)
19.(1)解:对于y=x2﹣5x+4,令y=0,则0=x2﹣5x+4,
∴x1=4,x2=1,
∴点A(1,0),点B(4,0),
令x=0,则y=4,
∴点C(0,4);
(2)解:四边形OCPQ为平行四边形,理由如下:
∵点B的坐标为(4,0),点C(0,4),
设直线BC的表达式为y=kx+b,
则,
解得,
∴直线BC的表达式为y=﹣x+4,
设点P的坐标为(x,﹣x+4),则点Q的坐标为(x,x2﹣5x+4),
则PQ=(﹣x+4)﹣(x2﹣5x+4)=﹣x2+4x=﹣(x﹣2)2+4,
∵﹣1<0,
故PQ有最大值,
当x=2时,PQ的最大值为4=CO,
∴PQ=CO,PQOC,
∴四边形OCPQ为平行四边形;
(3)解:∵D是OC的中点,点C(0,4),
∴点D(0,2),
由(2)知:当x=2时,PQ的最大值为4,
当x=2时,y=x2﹣5x+4=﹣2,
∴Q(2,﹣2),
由点D、Q的坐标,同理可得,直线DQ的表达式为y=﹣2x+2,
过点Q作QH⊥x轴于点H,
则QHCO,故∠AQH=∠ODQ,
而∠DQE=2∠ODQ.
∴∠HQA=∠HQE,
则直线AQ和直线QE关于直线QH对称,
∴设直线QE的表达式为y=2x+r,
将点Q的坐标代入上式并解得r=﹣6,
∴直线QE的表达式为y=2x﹣6,
联立y=x2﹣5x+4得,
解得或(不合题意,舍去),
∴点E的坐标为(5,4),
设点F的坐标为(0,m),
∴BE2=(5﹣4)2+(4﹣0)2=17,
BF2=m2+42=m2+16,
EF2=(m﹣4)2+52,
当BE=BF时,即16+m2=17,解得m=±1;
当BE=EF时,即25+(m﹣4)2=17,方程无解;
当BF=EF时,即16+m2=25+(m﹣4)2,解得m= ;
故点F的坐标为(0,1)或(0,﹣1)或(0,).
20.(1)对称轴为直线,的最大值为4,
(2)5
21.(1)a=1,b=-4
(2)n的值为-1
(3)m的值为4或6
