北师大版九年级下册1.5三角函数的应用同步练习(含答案)
文档属性
| 名称 | 北师大版九年级下册1.5三角函数的应用同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 726.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 11:37:02 | ||
图片预览


文档简介
1.5 三角函数的应用
同步练习
一、单选题
1.如图1,是我们经常看到的一种折叠桌子,它是由下面的支架AD、BC与桌面构成,如图2,已知OA=OB=OC=OD=20cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30cm B.60cm C.40cm D.60cm
2.如图,沿方向架桥,以桥两端出发,修公路和,测得,m,,则公路的长为( )
A.900m B.m C.m D.1800m
3.已知,斜坡的坡度i=1:2,小明沿斜坡的坡面走了100米,则小明上升的距离是( )
A.米 B.20米 C.米 D.米
4.如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿方向水平飞行进行航拍作业,与在同一铅直平面内,当无人机飞行至处时、测得景点的俯角为,景点的俯角为,此时到地面的距离为米,则两景点A、B间的距离为多少米(结果保留根号).( )
A.200米 B.300米 C.米 D.米
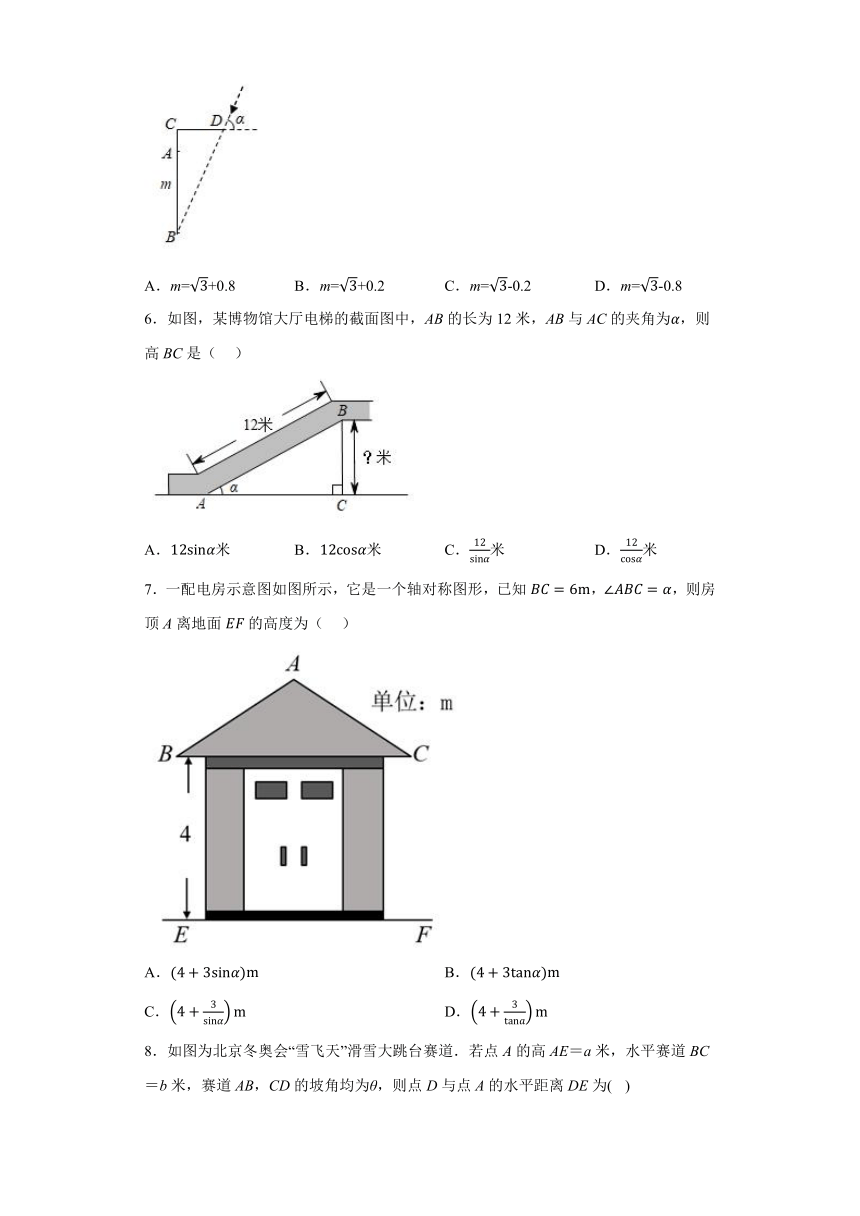
5.如图,窗子高AB=m米,窗子外面上方0.2米的点C处安装水平遮阳板CD=1米,当太阳光线与水平线成α=60°角时,光线刚好不能直接射人室内,则m的值是( )
A.m=+0.8 B.m=+0.2 C.m=-0.2 D.m=-0.8
6.如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为,则高BC是( )
A.米 B.米 C.米 D.米
7.一配电房示意图如图所示,它是一个轴对称图形,已知,,则房顶A离地面的高度为( )
A. B.
C. D.
8.如图为北京冬奥会“雪飞天”滑雪大跳台赛道.若点A的高AE=a米,水平赛道BC=b米,赛道AB,CD的坡角均为θ,则点D与点A的水平距离DE为( )
A.米 B.( b)米 C.(a-b)sinθ米 D.(a﹣b)cosθ米
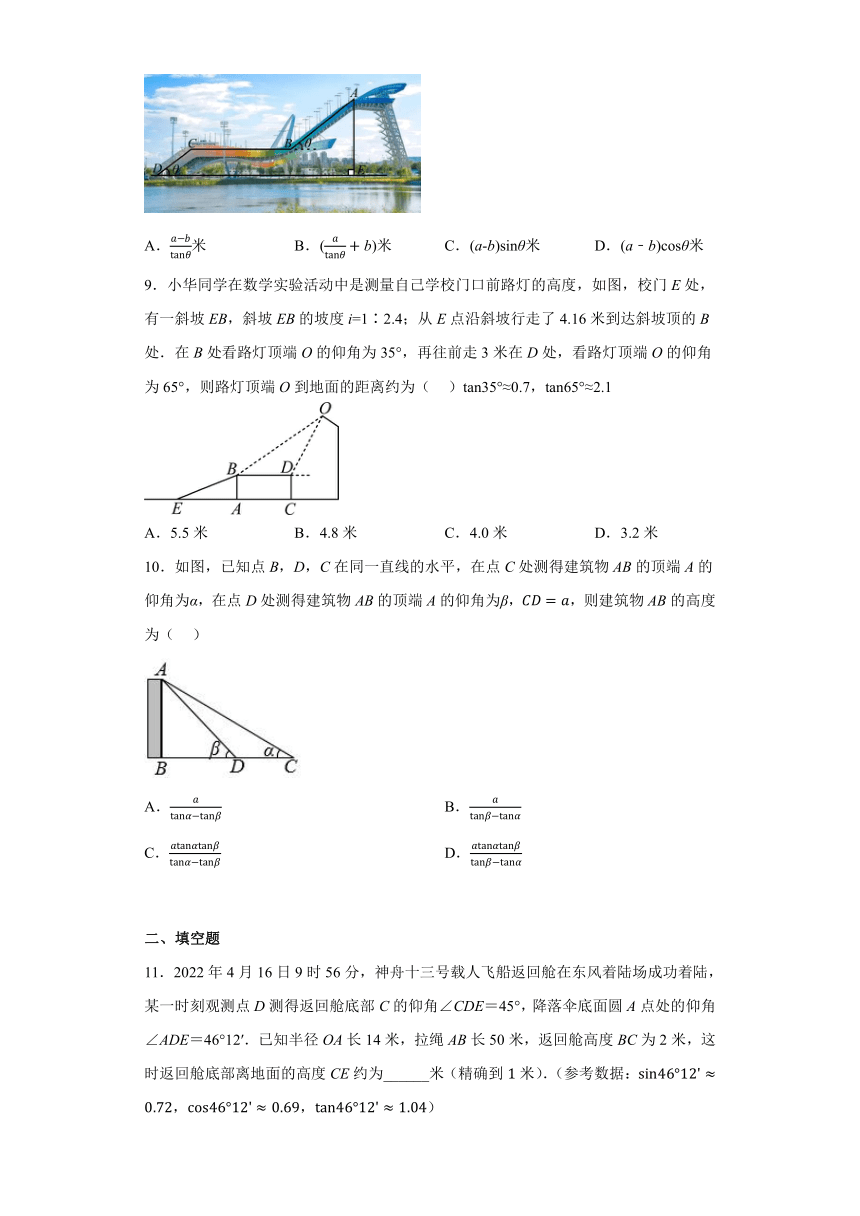
9.小华同学在数学实验活动中是测量自己学校门口前路灯的高度,如图,校门E处,有一斜坡EB,斜坡EB的坡度i=1∶2.4;从E点沿斜坡行走了4.16米到达斜坡顶的B处.在B处看路灯顶端O的仰角为35°,再往前走3米在D处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为( )tan35°≈0.7,tan65°≈2.1
A.5.5米 B.4.8米 C.4.0米 D.3.2米
10.如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β,,则建筑物AB的高度为( )
A. B.
C. D.
二、填空题
11.2022年4月16日9时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆,某一时刻观测点D测得返回舱底部C的仰角∠CDE=45°,降落伞底面圆A点处的仰角∠ADE=46°12′.已知半径OA长14米,拉绳AB长50米,返回舱高度BC为2米,这时返回舱底部离地面的高度CE约为______米(精确到米).(参考数据:,,)
12.喜迎二十大,“龙舟故里”赛龙舟.丹丹在汨罗江国际龙舟竞渡中心广场点处观看200米直道竞速赛.如图所示,赛道为东西方向,赛道起点位于点的北偏西方向上,终点位于点的北偏东方向上,米,则点到赛道的距离约为______米(结果保留整数,参考数据:).
13.东太湖风景区美丽怡人,如意桥似浮在太湖之上富有灵动起飞的光环.小亮在如意桥上看到一艘游艇迎面驶来,他在高出水面的A处测得在C处的游艇俯角为;他登高到正上方的B处测得驶至D处的游艇俯角为,则两次观测期间游艇前进了___________米.(结果精确到,参考数据:)
14.如图,点P,A,B,C在同一平面内,点A,B,C在同一直线上,且PC⊥AC,在点A处测得点P在北偏东60°方向上,在点B处测得点P在北偏东30°方向上,若AP=12千米,则A,B两点的距离为 ___千米.
15.如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1:,则斜坡AB的长是__________米.
三、解答题
16.某学校九年级的学生去参加社会实践,在风景区看到一棵古松,不知这棵古松有多高,下面是他们的一段对话:
甲:我站在此处看树顶仰角为45°.
乙:我站在此处看树顶仰角为30°.
甲:我们的身高都是1.5m.
乙:我们俩相距20m.
请你根据两位同学的对话,计算这棵古松DE的高度.(结果保留根号).
17.如图,某登山队沿山坡上山后,再沿山坡CD下山.已知山坡AB的坡度为,山坡BC的坡度为,山坡CD的坡角∠D=30°,且山顶C点到水平面AD的距离为1000m,B点到水平面AD的距离为200m.
(1)求山坡的长,
(2)已知登山队上山的速度保持不变,且下山速度是上山速度的2倍,若下山比上山少用26分钟,求下山的速度.
18.随着我国科学技术的不断发展,5G移动通信技术日趋完善.某市政府为了实现5G网络全覆盖,2021~2025年拟建设5G基站3000个,如图,在斜坡上有一建成的5G基站塔,小明在坡脚处测得塔顶的仰角为,然后他沿坡面行走了50米到达处,处离地平面的距离为30米且在处测得塔顶的仰角.(点、、、、均在同一平面内,为地平线)(参考数据:,,)
(1)求坡面的坡度;
(2)求基站塔的高.
19.如图,某公路紧邻一个山坡,坡面CD与地平面AB平行,斜坡AC=30米,坡比i=1:,为防止山体滑坡,有关单位准备对斜坡进行改造,将斜坡AC改为AE,坡角为,请求出CE的长.(结果精确到0.1米,参考数据:,,)
20.李威在A处看一棵大树的顶端D处的仰角是30°,向树的方向前进30米到B处看树顶D处的仰角是60°,李威的眼睛离地面高米,已知,E、F、G在一条直线上,求树高 是多少?(结果保留根号)
21.如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面,坡角.在阳光下,小明观察到在地面上的影长为,在坡面上的影长为.同一时刻,小明测得直立于地面长60cm的木杆的影长为90cm(其影子完全落在地面上).求立柱AB的高度.
参考答案:
1.D2.B3.A4.C5.C6.A7.B8.B9.B10.D
11.1614
12.87
13.36
14.
15.
16.(m)
17.(1)1520m
(2)下山的速度是每分钟40米
18.(1)
(2)基站塔的高为米
19.4.4米
20.树的高是米
21.(170+60)cm
同步练习
一、单选题
1.如图1,是我们经常看到的一种折叠桌子,它是由下面的支架AD、BC与桌面构成,如图2,已知OA=OB=OC=OD=20cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30cm B.60cm C.40cm D.60cm
2.如图,沿方向架桥,以桥两端出发,修公路和,测得,m,,则公路的长为( )
A.900m B.m C.m D.1800m
3.已知,斜坡的坡度i=1:2,小明沿斜坡的坡面走了100米,则小明上升的距离是( )
A.米 B.20米 C.米 D.米
4.如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿方向水平飞行进行航拍作业,与在同一铅直平面内,当无人机飞行至处时、测得景点的俯角为,景点的俯角为,此时到地面的距离为米,则两景点A、B间的距离为多少米(结果保留根号).( )
A.200米 B.300米 C.米 D.米
5.如图,窗子高AB=m米,窗子外面上方0.2米的点C处安装水平遮阳板CD=1米,当太阳光线与水平线成α=60°角时,光线刚好不能直接射人室内,则m的值是( )
A.m=+0.8 B.m=+0.2 C.m=-0.2 D.m=-0.8
6.如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为,则高BC是( )
A.米 B.米 C.米 D.米
7.一配电房示意图如图所示,它是一个轴对称图形,已知,,则房顶A离地面的高度为( )
A. B.
C. D.
8.如图为北京冬奥会“雪飞天”滑雪大跳台赛道.若点A的高AE=a米,水平赛道BC=b米,赛道AB,CD的坡角均为θ,则点D与点A的水平距离DE为( )
A.米 B.( b)米 C.(a-b)sinθ米 D.(a﹣b)cosθ米
9.小华同学在数学实验活动中是测量自己学校门口前路灯的高度,如图,校门E处,有一斜坡EB,斜坡EB的坡度i=1∶2.4;从E点沿斜坡行走了4.16米到达斜坡顶的B处.在B处看路灯顶端O的仰角为35°,再往前走3米在D处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为( )tan35°≈0.7,tan65°≈2.1
A.5.5米 B.4.8米 C.4.0米 D.3.2米
10.如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β,,则建筑物AB的高度为( )
A. B.
C. D.
二、填空题
11.2022年4月16日9时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆,某一时刻观测点D测得返回舱底部C的仰角∠CDE=45°,降落伞底面圆A点处的仰角∠ADE=46°12′.已知半径OA长14米,拉绳AB长50米,返回舱高度BC为2米,这时返回舱底部离地面的高度CE约为______米(精确到米).(参考数据:,,)
12.喜迎二十大,“龙舟故里”赛龙舟.丹丹在汨罗江国际龙舟竞渡中心广场点处观看200米直道竞速赛.如图所示,赛道为东西方向,赛道起点位于点的北偏西方向上,终点位于点的北偏东方向上,米,则点到赛道的距离约为______米(结果保留整数,参考数据:).
13.东太湖风景区美丽怡人,如意桥似浮在太湖之上富有灵动起飞的光环.小亮在如意桥上看到一艘游艇迎面驶来,他在高出水面的A处测得在C处的游艇俯角为;他登高到正上方的B处测得驶至D处的游艇俯角为,则两次观测期间游艇前进了___________米.(结果精确到,参考数据:)
14.如图,点P,A,B,C在同一平面内,点A,B,C在同一直线上,且PC⊥AC,在点A处测得点P在北偏东60°方向上,在点B处测得点P在北偏东30°方向上,若AP=12千米,则A,B两点的距离为 ___千米.
15.如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1:,则斜坡AB的长是__________米.
三、解答题
16.某学校九年级的学生去参加社会实践,在风景区看到一棵古松,不知这棵古松有多高,下面是他们的一段对话:
甲:我站在此处看树顶仰角为45°.
乙:我站在此处看树顶仰角为30°.
甲:我们的身高都是1.5m.
乙:我们俩相距20m.
请你根据两位同学的对话,计算这棵古松DE的高度.(结果保留根号).
17.如图,某登山队沿山坡上山后,再沿山坡CD下山.已知山坡AB的坡度为,山坡BC的坡度为,山坡CD的坡角∠D=30°,且山顶C点到水平面AD的距离为1000m,B点到水平面AD的距离为200m.
(1)求山坡的长,
(2)已知登山队上山的速度保持不变,且下山速度是上山速度的2倍,若下山比上山少用26分钟,求下山的速度.
18.随着我国科学技术的不断发展,5G移动通信技术日趋完善.某市政府为了实现5G网络全覆盖,2021~2025年拟建设5G基站3000个,如图,在斜坡上有一建成的5G基站塔,小明在坡脚处测得塔顶的仰角为,然后他沿坡面行走了50米到达处,处离地平面的距离为30米且在处测得塔顶的仰角.(点、、、、均在同一平面内,为地平线)(参考数据:,,)
(1)求坡面的坡度;
(2)求基站塔的高.
19.如图,某公路紧邻一个山坡,坡面CD与地平面AB平行,斜坡AC=30米,坡比i=1:,为防止山体滑坡,有关单位准备对斜坡进行改造,将斜坡AC改为AE,坡角为,请求出CE的长.(结果精确到0.1米,参考数据:,,)
20.李威在A处看一棵大树的顶端D处的仰角是30°,向树的方向前进30米到B处看树顶D处的仰角是60°,李威的眼睛离地面高米,已知,E、F、G在一条直线上,求树高 是多少?(结果保留根号)
21.如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面,坡角.在阳光下,小明观察到在地面上的影长为,在坡面上的影长为.同一时刻,小明测得直立于地面长60cm的木杆的影长为90cm(其影子完全落在地面上).求立柱AB的高度.
参考答案:
1.D2.B3.A4.C5.C6.A7.B8.B9.B10.D
11.1614
12.87
13.36
14.
15.
16.(m)
17.(1)1520m
(2)下山的速度是每分钟40米
18.(1)
(2)基站塔的高为米
19.4.4米
20.树的高是米
21.(170+60)cm
