1 密铺(课件)四年级下册数学北师大版(共13张PPT)
文档属性
| 名称 | 1 密铺(课件)四年级下册数学北师大版(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 991.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
第1课时 密铺
数 学 好 玩
1.通过观察生活中常见的密铺图案,初步理解密铺的含义。
2.通过拼摆各种图形,探索密铺的特点,认识一些可以密铺的平面图形。
3.在探究多边形密铺条件的过程中提升观察、猜测、验证、推理和交流的能力。
4.能运用几种图形进行简单的密铺设计和面积计算。
重点:掌握密铺的特点,知道哪些图形可以进行密铺。
难点:理解密铺的特点,能进行简单的密铺设计。
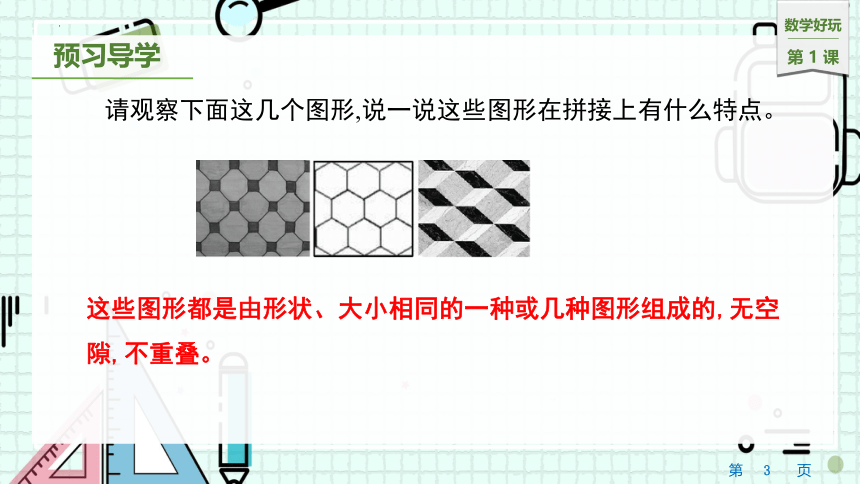
请观察下面这几个图形,说一说这些图形在拼接上有什么特点。
这些图形都是由形状、大小相同的一种或几种图形组成的,无空隙,不重叠。
采取让学生动手试一试的方法,圆形在铺地时有缝,用正方形密铺就没有缝,顺势揭示出密铺的定义,让学生自己感受铺与密铺的区别,从而理解什么是密铺。让学生经历“猜想——验证——发现——总结”的自主探究的学习过程,体验到探究成功的快乐。
任务驱动
1.什么是密铺 平面图形密铺的特点是什么
把形状、大小相同的一种或几种平面图形不留空隙、不重叠地拼接在一起,这就是密铺。
平面图形密铺的特点:
(1)用一种或几种全等图形进行拼接。
(2)拼接处不留空隙、不重叠。
(3)能连续铺成一片。
2.三角形能不能密铺 四边形可不可以 请将剪好的三角形或四边形拼一拼, 摆一摆。
都可以密铺。
3.动手试一试,如果只用一种图形,下面哪些图形可以密铺 哪些图形不可以密铺
和 不能密铺,其他都可以密铺。
4.请按照下面的方法试一试,你有什么发现 说说符合密铺要求的多边形应该具备什么样的条件。
密铺与图形的角有关。进行密铺时必须使每个拼接点处的内角和度数为360度,否则不能进行密铺。
5.观察下面的密铺图案,想一想它们是如何形成的。
略
归纳总结
1.三角形的内角和是180°,用几个相同的三角形拼接时,每个角只需用两次,就能拼出一个周角,所以三角形一定可以密铺。
2.任意四边形的四个内角之和是360°,它的四个角刚好能拼成一个周角,所以任意四边形一定可以密铺。
3.正六边形的每个内角都是120°,也能拼接出周角,所以正六边形可以密铺。
4.只用正五边形一种图形不能密铺。
1.在下面给出的平面图形中,不能密铺的是( )。
A.三角形 B.四边形 C.正五边形 D.正六边形
2.当围绕一点拼在一起的几个多边形的内角加在一起组成一个 ( )时,这个多边形就可以密铺。
A.45°角 B.平角 C.周角 D.直角
C
C
3.只用等边三角形与正方形两种图形是否可以密铺 如果可以,请画出图形。( 实践类作业)
60° +60° +60° +90° +90° =360° 可以密铺。
答:因为3个60° 和2个90° 的角合起来是360° ,所以只用等边三角形与正方形两种图形是可以密铺的。
END
感谢观看 下节课再会
第1课时 密铺
数 学 好 玩
1.通过观察生活中常见的密铺图案,初步理解密铺的含义。
2.通过拼摆各种图形,探索密铺的特点,认识一些可以密铺的平面图形。
3.在探究多边形密铺条件的过程中提升观察、猜测、验证、推理和交流的能力。
4.能运用几种图形进行简单的密铺设计和面积计算。
重点:掌握密铺的特点,知道哪些图形可以进行密铺。
难点:理解密铺的特点,能进行简单的密铺设计。
请观察下面这几个图形,说一说这些图形在拼接上有什么特点。
这些图形都是由形状、大小相同的一种或几种图形组成的,无空隙,不重叠。
采取让学生动手试一试的方法,圆形在铺地时有缝,用正方形密铺就没有缝,顺势揭示出密铺的定义,让学生自己感受铺与密铺的区别,从而理解什么是密铺。让学生经历“猜想——验证——发现——总结”的自主探究的学习过程,体验到探究成功的快乐。
任务驱动
1.什么是密铺 平面图形密铺的特点是什么
把形状、大小相同的一种或几种平面图形不留空隙、不重叠地拼接在一起,这就是密铺。
平面图形密铺的特点:
(1)用一种或几种全等图形进行拼接。
(2)拼接处不留空隙、不重叠。
(3)能连续铺成一片。
2.三角形能不能密铺 四边形可不可以 请将剪好的三角形或四边形拼一拼, 摆一摆。
都可以密铺。
3.动手试一试,如果只用一种图形,下面哪些图形可以密铺 哪些图形不可以密铺
和 不能密铺,其他都可以密铺。
4.请按照下面的方法试一试,你有什么发现 说说符合密铺要求的多边形应该具备什么样的条件。
密铺与图形的角有关。进行密铺时必须使每个拼接点处的内角和度数为360度,否则不能进行密铺。
5.观察下面的密铺图案,想一想它们是如何形成的。
略
归纳总结
1.三角形的内角和是180°,用几个相同的三角形拼接时,每个角只需用两次,就能拼出一个周角,所以三角形一定可以密铺。
2.任意四边形的四个内角之和是360°,它的四个角刚好能拼成一个周角,所以任意四边形一定可以密铺。
3.正六边形的每个内角都是120°,也能拼接出周角,所以正六边形可以密铺。
4.只用正五边形一种图形不能密铺。
1.在下面给出的平面图形中,不能密铺的是( )。
A.三角形 B.四边形 C.正五边形 D.正六边形
2.当围绕一点拼在一起的几个多边形的内角加在一起组成一个 ( )时,这个多边形就可以密铺。
A.45°角 B.平角 C.周角 D.直角
C
C
3.只用等边三角形与正方形两种图形是否可以密铺 如果可以,请画出图形。( 实践类作业)
60° +60° +60° +90° +90° =360° 可以密铺。
答:因为3个60° 和2个90° 的角合起来是360° ,所以只用等边三角形与正方形两种图形是可以密铺的。
END
感谢观看 下节课再会
