18.1.1平行四边形的性质(1)
文档属性
| 名称 | 18.1.1平行四边形的性质(1) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-18 14:01:43 | ||
图片预览





文档简介
课件25张PPT。18.1.1 平行四边形的定义和性质(一)八年级(6)班
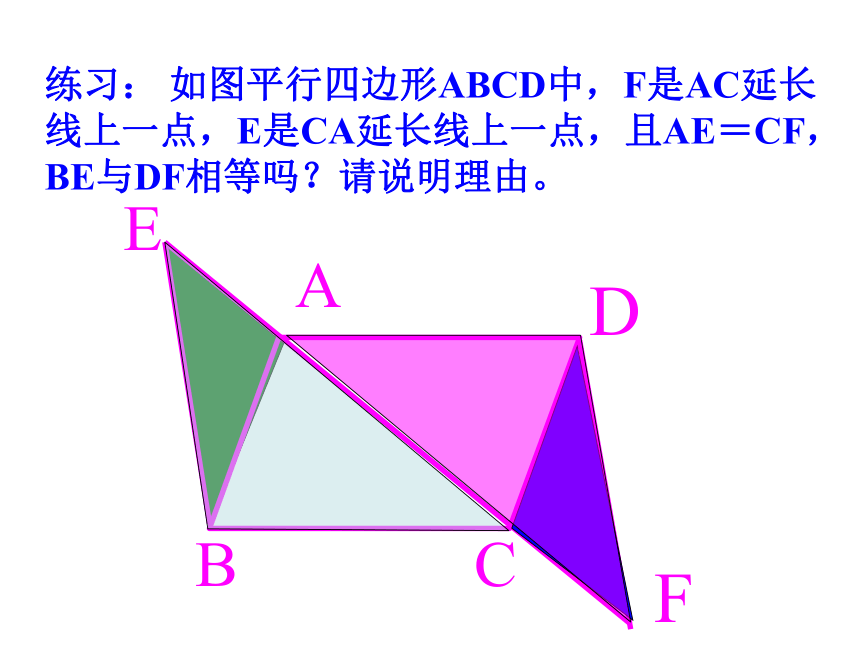
付美玲练习: 如图平行四边形ABCD中,F是AC延长线上一点,E是CA延长线上一点,且AE=CF,BE与DF相等吗?请说明理由。学习目标:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角相等的性质;
3.初步体会几何研究的一般思路与方法.
学习重点:
平行四边形边角性质的证明和应用.
学习难点:
平行四边形边角性质的证明推理过程观察生活中的这些图片,它们是否都有平行四边形的形象? 观察抽象 形成概念 你还记得平行四边形的定义吗?
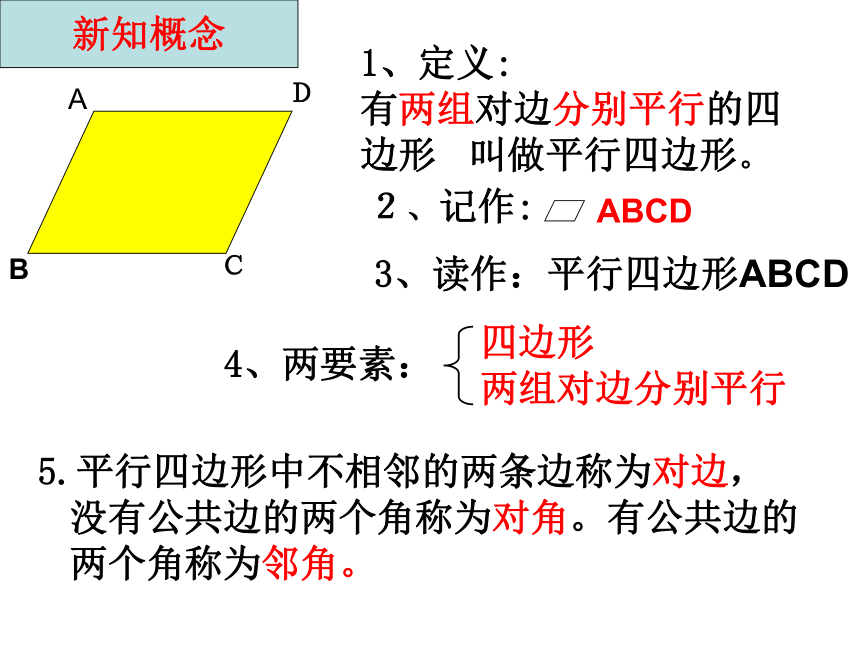
两组对边分别平行的四边形叫做平行四边形.1、定义:
有两组对边分别平行的四边形 叫做平行四边形。2、记作:4、两要素: ABCD3、读作:平行四边形ABCD5.平行四边形中不相邻的两条边称为对边,没有公共边的两个角称为对角。有公共边的两个角称为邻角。新知概念反之:∴ AB∥CD,AD∥BC∵四边形ABCD是平行四边形、6、几何语言:
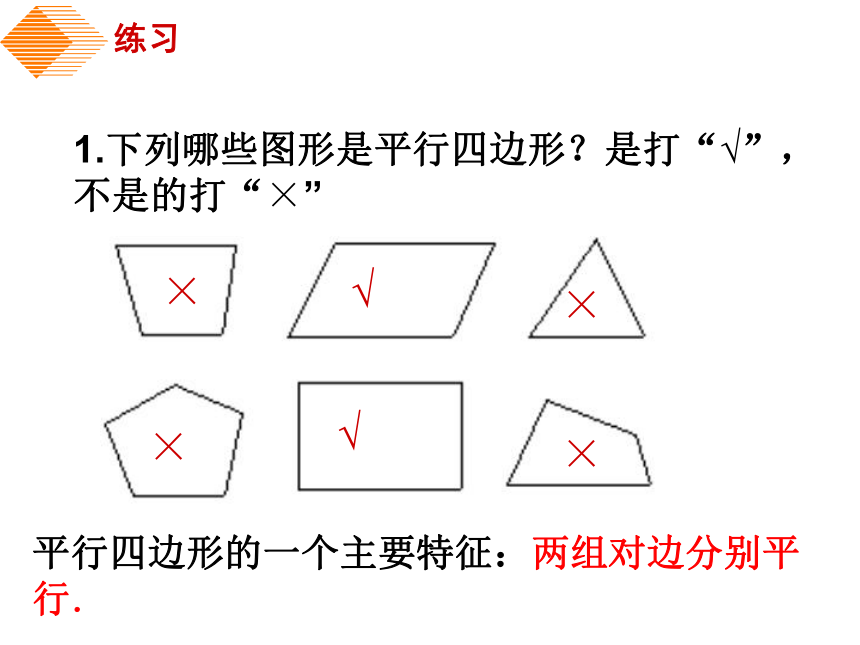
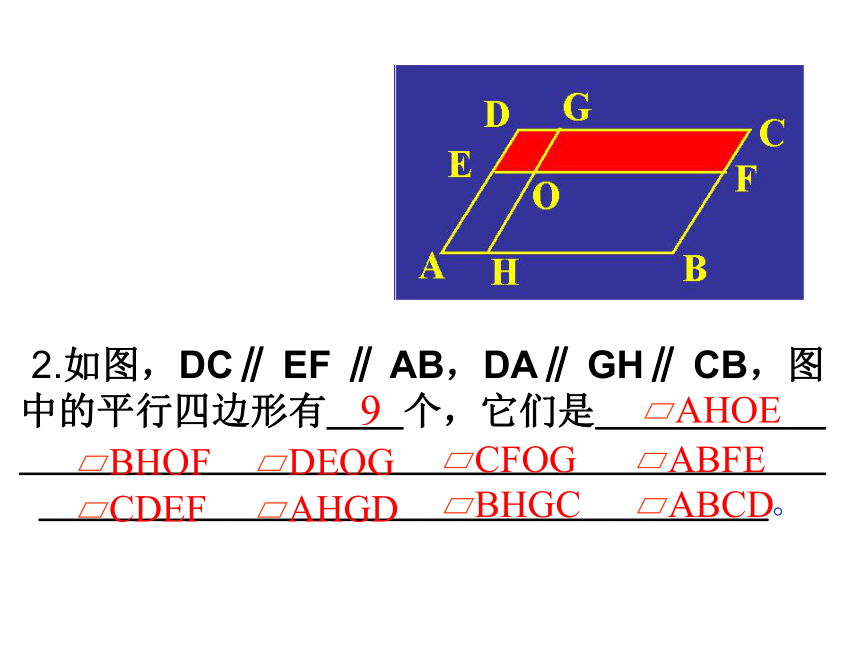
在四边形ABCD中,∴四边形ABCD是平行四边形. ∵ AB∥CD,AD∥BC练习1.下列哪些图形是平行四边形?是打“√”,不是的打“×”平行四边形的一个主要特征:两组对边分别平行.××××√√ 2.如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是______________________________________________。9CD步骤1:画两条平行线;步骤2:在两条线上分别取点A和点B,连结AB;新知认识画一画平行四边形:即∠BAD=∠DCB证明:连结AC∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,AC=CA,∠3=∠4∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3ABCD32cm30cm56°124°124° 小试牛刀:小结:平行四边形中知道其中一角可求出另外三个角的度数。 例题教学: ? 例2 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?解:∵四边形ABCD是平行四边形∵ AB=8随堂练习: ? 4030120°120°60°120°40°感悟与收获1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的性质: 平行四边形的对边平行且相等;平行四边形的对角相等。作业:P91习题19.1第1、2题例1、已知 ABCD中,∠A=40°,求其他各个内角的度数。∴∠D=∠B=140°
解:∴∠C=∠A=40°又∵AD∥BC∴∠B=180°-∠A=180°-40°∴∠A+∠B=180°=140°下课了,同学们再见归纳平行四边形的性质ABCD平行四边形的性质:边平行四边形的对边平行且相等;角平行四边形的对角相等;邻角互补;平行四边形是中心对称图形。对称性对角线平行四边形的对角互相平分;平行四边形的性质(数学表达式)∵四边形ABCD是平行四边形
∴ AB∥CD, AD∥BC
AB = CD, AD= BC∵四边形ABCD是平行四边形
∴ ∠A=∠C, ∠B=∠D∵ AB∥CD
∴ ∠A+∠D=1800, ∠B+∠C=1800平行四边形的对边平行且相等;平行四边形的对角相等,邻角互补;∵四边形ABCD是平行四边形
∴ OA = OC , OB = OD 平行四边形的对角线互相平分;知识的应用例1、已知 ABCD中,∠A=40°,你能求出其他各角的度数吗?说说你的理由。知识的应用(例题规范格式书写)解:∵在 ABCD中,∠A=40°,
∴∠ C=∠A=40°, ∠B= ∠D
(平行四边形的对角相等)
又∵AD∥BC,
∴ ∠ B+∠A=180°,
(两直线平行,同旁内角互补)
∴ ∠ B=180°-∠A
=180°-40°
=140°
∴∠D=∠B=40°
(平行四边形的对角相等)知识的应用1、已知在 ABCD中,∠A=120°,求出其余各内角的度数解: ∵在 ABCD中,∠A=120°,
∴∠ C= = D
( )
又∵AD∥BC,
∴ ∠ A+∠ B = ,
( )
∴ ∠ B= - ?= - = ?? ?
∴∠ D= = D
( ) ??????????????
∴∠D=∠B=60°(平行四边形的对角相等)∠A120°180°两直线平行,同旁内角互补平行四边形的对角相等180°∠ A120°180°60°∠ B60°平行四边形的对角相等知识的应用2.如图:在 ABCD中,已知?A+?C=100°,
则?A = ,?B= ,?C= ,
?D= 。50°130°50°130°60°120°60°120°知识的应用 例2、如图,小明用一根24m长的绳子围成了一个 平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 8知识的应用(例题规范格式书写) 解:在 ABCD中,AB=8(m)
∴AB=CD=8(m),AD=BC
(平行四边形的对边相等)
又∵AB+BC+CD+AD=24 (m)
∴ 8+BC+8+BC=24 (m)
∴ 16+2BC=24 (m)
∴ BC=4 (m)
∴AD=BC=4 (m).8
付美玲练习: 如图平行四边形ABCD中,F是AC延长线上一点,E是CA延长线上一点,且AE=CF,BE与DF相等吗?请说明理由。学习目标:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角相等的性质;
3.初步体会几何研究的一般思路与方法.
学习重点:
平行四边形边角性质的证明和应用.
学习难点:
平行四边形边角性质的证明推理过程观察生活中的这些图片,它们是否都有平行四边形的形象? 观察抽象 形成概念 你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.1、定义:
有两组对边分别平行的四边形 叫做平行四边形。2、记作:4、两要素: ABCD3、读作:平行四边形ABCD5.平行四边形中不相邻的两条边称为对边,没有公共边的两个角称为对角。有公共边的两个角称为邻角。新知概念反之:∴ AB∥CD,AD∥BC∵四边形ABCD是平行四边形、6、几何语言:
在四边形ABCD中,∴四边形ABCD是平行四边形. ∵ AB∥CD,AD∥BC练习1.下列哪些图形是平行四边形?是打“√”,不是的打“×”平行四边形的一个主要特征:两组对边分别平行.××××√√ 2.如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是______________________________________________。9CD步骤1:画两条平行线;步骤2:在两条线上分别取点A和点B,连结AB;新知认识画一画平行四边形:即∠BAD=∠DCB证明:连结AC∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,AC=CA,∠3=∠4∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3ABCD32cm30cm56°124°124° 小试牛刀:小结:平行四边形中知道其中一角可求出另外三个角的度数。 例题教学: ? 例2 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?解:∵四边形ABCD是平行四边形∵ AB=8随堂练习: ? 4030120°120°60°120°40°感悟与收获1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的性质: 平行四边形的对边平行且相等;平行四边形的对角相等。作业:P91习题19.1第1、2题例1、已知 ABCD中,∠A=40°,求其他各个内角的度数。∴∠D=∠B=140°
解:∴∠C=∠A=40°又∵AD∥BC∴∠B=180°-∠A=180°-40°∴∠A+∠B=180°=140°下课了,同学们再见归纳平行四边形的性质ABCD平行四边形的性质:边平行四边形的对边平行且相等;角平行四边形的对角相等;邻角互补;平行四边形是中心对称图形。对称性对角线平行四边形的对角互相平分;平行四边形的性质(数学表达式)∵四边形ABCD是平行四边形
∴ AB∥CD, AD∥BC
AB = CD, AD= BC∵四边形ABCD是平行四边形
∴ ∠A=∠C, ∠B=∠D∵ AB∥CD
∴ ∠A+∠D=1800, ∠B+∠C=1800平行四边形的对边平行且相等;平行四边形的对角相等,邻角互补;∵四边形ABCD是平行四边形
∴ OA = OC , OB = OD 平行四边形的对角线互相平分;知识的应用例1、已知 ABCD中,∠A=40°,你能求出其他各角的度数吗?说说你的理由。知识的应用(例题规范格式书写)解:∵在 ABCD中,∠A=40°,
∴∠ C=∠A=40°, ∠B= ∠D
(平行四边形的对角相等)
又∵AD∥BC,
∴ ∠ B+∠A=180°,
(两直线平行,同旁内角互补)
∴ ∠ B=180°-∠A
=180°-40°
=140°
∴∠D=∠B=40°
(平行四边形的对角相等)知识的应用1、已知在 ABCD中,∠A=120°,求出其余各内角的度数解: ∵在 ABCD中,∠A=120°,
∴∠ C= = D
( )
又∵AD∥BC,
∴ ∠ A+∠ B = ,
( )
∴ ∠ B= - ?= - = ?? ?
∴∠ D= = D
( ) ??????????????
∴∠D=∠B=60°(平行四边形的对角相等)∠A120°180°两直线平行,同旁内角互补平行四边形的对角相等180°∠ A120°180°60°∠ B60°平行四边形的对角相等知识的应用2.如图:在 ABCD中,已知?A+?C=100°,
则?A = ,?B= ,?C= ,
?D= 。50°130°50°130°60°120°60°120°知识的应用 例2、如图,小明用一根24m长的绳子围成了一个 平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 8知识的应用(例题规范格式书写) 解:在 ABCD中,AB=8(m)
∴AB=CD=8(m),AD=BC
(平行四边形的对边相等)
又∵AB+BC+CD+AD=24 (m)
∴ 8+BC+8+BC=24 (m)
∴ 16+2BC=24 (m)
∴ BC=4 (m)
∴AD=BC=4 (m).8
