2022-2023学年苏科版七年级数学上册 3.2 代数式 练习题 (含解析)
文档属性
| 名称 | 2022-2023学年苏科版七年级数学上册 3.2 代数式 练习题 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 142.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 13:24:41 | ||
图片预览




文档简介
3.2 代数式(练习题)-苏科版七年级上册
一.选择题
.将正整数按如图所示的位置顺序排列:
根据排列规律,则2022应在( )
A.点A处 B.点B处 C.点C处 D.点D处
.某商品每次降价20%,连续两次降价后的价格为m元,则原价为( )
A.1.2m元 B.元 C.元 D.0.82m元
.一个矩形的周长为l,若矩形的长为a,则该矩形的宽为( )
A.﹣a B. C.l﹣a D.
.观察下列各数:1,,,,…,按照你发现的规律,这列数的第6个数是( )
A. B. C. D.
.下列图形都是由圆和几个黑色围棋子按一定规律组成,图①中有4个黑色棋子,图②中有7个黑色棋子,图③中有10个黑色棋子,…,依次规律,图中黑色棋子的个数是( )
A.6067 B.6066 C.6065 D.6064
.按一定规律排列的一组数据:,﹣,,﹣,,﹣,….则按此规律排列的第10个数是( )
A.﹣ B. C.﹣ D.
.观察图中正方形四个顶点所标的数字规律,可知数2022应标在( )
A.第506个正方形的右上角
B.第506个正方形的左下角
C.第505个正方形的右上角
D.第505个正方形的左下角
.(n为正整数)一定等于( )
A.an+2 B.2a2 C. D.a2n
.《孙子算经》中有一个问题:今有甲、乙、丙三人持钱.甲语乙、丙:“各将公等所持钱半以益我,钱成九十.”乙复语甲、丙:“各将公等所持钱半以益我,钱成七十.”丙复语甲、乙:“各将公等所持钱半以益我,钱成五十六.”若设甲、乙各持钱数为x、y,则丙持钱数不可以表示为( )
A. B.180﹣2x﹣y C.140﹣2x﹣y D.140﹣x﹣2y
.长为acm,宽为bcm(a>b>5)的长方形,若将长增加5cm,宽减少5cm,则它的面积会( )
A.变小 B.变大 C.不变 D.无法确定
二.填空题
.有一组单项式依次为:﹣x2,,﹣,,﹣,…,则第n个单项式是 .
.某种桔子的售价是每千克3元,用面值为100元的人民币购买了a千克,应找回 元.
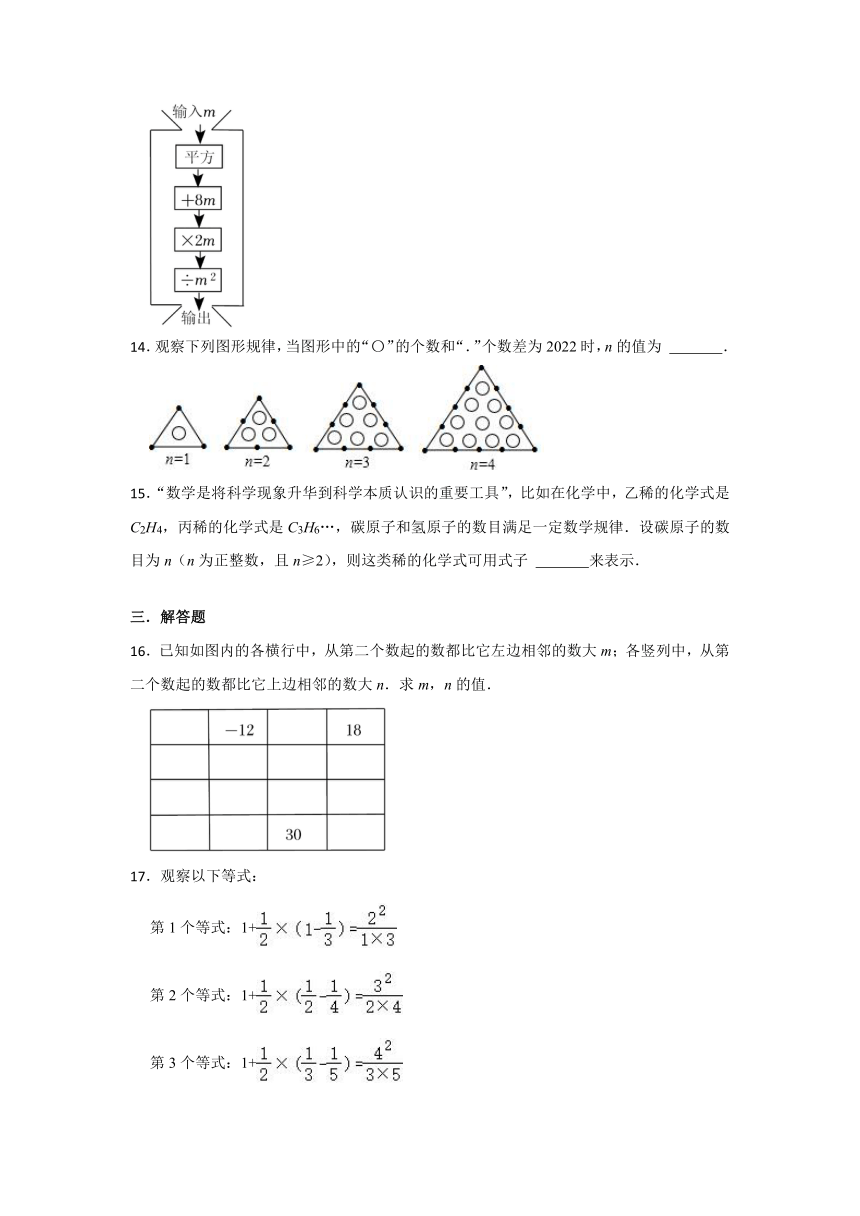
.输入m,按照如图所示的程序进行计算后,输出的结果为 .(用含m的代数式表示)
.观察下列图形规律,当图形中的“〇”的个数和“.”个数差为2022时,n的值为 .
.“数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,乙稀的化学式是C2H4,丙稀的化学式是C3H6…,碳原子和氢原子的数目满足一定数学规律.设碳原子的数目为n(n为正整数,且n≥2),则这类稀的化学式可用式子 来表示.
三.解答题
.已知如图内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中,从第二个数起的数都比它上边相邻的数大n.求m,n的值.
.观察以下等式:
第1个等式:1+
第2个等式:1+
第3个等式:1+
第4个等式:1+
按照以上规律,解决下列问题:
(1)写出第5个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示),并证明.
.某居民小区为响应党的号召,开展全民健身活动,准备修建一座长方形健身广场,其设计方案及数据如图所示.已知广场内A区为长方形的成年人活动场所,B区为圆形的儿童活动场所,其余地方为绿化带.
(1)求绿化带的面积;
(2)求整座健身广场的面积是成年人活动场所面积的多少倍.
.设a1,a2,a3,…a2021,a2022都是正数,
M=(a1+a2+…a2021) (a2+a3+…a2022),
N=(a1+a2+…a2022) (a2+a3+…a2021),
试比较M、N的大小.
.某水果店主计划采购A、B两种水果100kg进行销售,其中A水果的进货量(取整数)不小于28kg,下表为这两种水果的进货价、销售价及损耗率:
项目 进货价(元/kg) 销售价(元/kg) 损耗率
A水果 20 35 20%
B水果 5 6 5%
经预算,该店主准备采购的总资金不高于950元.
(1)请你为店主设计有几种采购方案,请写出具体方案;
(2)设采购A水果akg,请用含有a字母的代数式(化简后)表示采购A、B两种水果销售后所获取的利润;在(1)方案中,最多获取利润是多少元?
参考答案与试题解析
一.选择题
.【解答】解:由题意得:在A位置的数被4除余2,在B位置的数被4除余3,在C位置的数被4整除,在D位置的数被4除余1;
2022÷4=505……2,
∴2022应在2的位置,也就是在A处.
故答案为:A.
.【解答】解:原价为:(元);
故选:B.
.【解答】解:矩形的宽为:.
故选:A.
.【解答】解:∵1=,
=,
=,
=,
…,
∴第n个数为:,
∴第6个数为:.
故选:C.
.【解答】解:∵图①中有3+1=4个黑色棋子,
图②中有3×2+1=7个黑色棋子,
图③中有3×3+1=10个黑色棋子,
…
图n中黑色棋子的个数是3n+1,
∴图2022中黑色棋子的个数是3×2022+1=6067.
故选:A.
.【解答】解:原数据可转化为:,﹣,,﹣,,﹣,…,
∴=(﹣1)1+1×,
﹣=(﹣1)2+1×,
=(﹣1)3+1×,
...
∴第n个数为:(﹣1)n+1,
∴第10个数为:(﹣1)10+1×=﹣.
故选:A.
.【解答】解:根据图形的变化可知,每四个数一个正方形,且四个数在正方形上的相对位置是相同的,
∵2022÷4=505……2,
∴2022在第506个正方形右上角位置上,
故选:A.
.【解答】解:
=(an)2
=a2n.
故选:D.
.【解答】解:设丙持钱数为z,
根据丙语得z+=56,
整理得z=56﹣,
故A选项不符合题意;
根据甲语得x+=90,
整理得z=180﹣2x﹣y,
故B选项不符合题意;
根据乙语得y+=70,
整理得z=140﹣x﹣2y,
故D选项不符合题意,C选项符合题意.
故选:C.
.【解答】解:原长方形的面积为:abcm2,
现长方形的面积为:(a+5)(b﹣5)=(ab+5b﹣5a﹣25)cm2,
因为b<a,
所以b﹣a<0,
所以ab+5b﹣5a﹣25﹣ab=5(b﹣a)﹣25<0,
即现长方形的面积小于原长方形的面积.
故选:A.
二.填空题
.【解答】解:∵﹣x2=(﹣1)1,
=(﹣1)2,
﹣=(﹣1)3,
……,
∴第n个单项式为:.
故答案为:.
.【解答】解:根据题意,a千克桔子售价为3a元,所以应找回(100﹣3a)元.
故答案为:(100﹣3a).
.【解答】解:根据题意得:(m2+8m)×2m÷m2
=m2(m+8)×2÷m2
=(m+8)×2
=2m+16.
故答案为:2m+16.
.【解答】解:∵n=1时,“ ”的个数是3=3×1;
n=2时,“ ”的个数是6=3×2;
n=3时,“ ”的个数是9=3×3;
n=4时,“ ”的个数是12=3×4;
……,
∴第n个图形中“ ”的个数是3n;
又∵n=1时,“〇”的个数是1=;
n=2时,“〇”的个数是3=,
n=3时,“〇”的个数是6=,
n=4时,“〇”的个数是10=,
……,
∴第n个“〇”的个数是,
由图形中的“〇”的个数和“.”个数差为2022,
∴①,②,
解①得:无解,
解②得:,n.
故答案为:不存在.
.【解答】解:根据题意,这类稀的化学式为 nH2n.
故答案为: nH2n.
三.解答题
.【解答】解:∵各横行中,从第二个数起的数都比它左边相邻的数大m,
∴﹣12+2m=18,
解得m=15.
又∵各竖列中,从第二个数起的数都比它上边相邻的数大n,
∴(﹣12+m)+3n=30,
将m=15代入上述方程得 3+3n=30,
解得n=9.
.【解答】解:(1)第5个等式为:,
故答案为:;
(2)猜想:第n个等式为为:,
证明:等式左边=1+
=1+
=
==右边,
故猜想成立.
故答案为:.
.【解答】解:(1)绿化带的面积:(a+4a+5a)(1.5a+3a+1.5a) ﹣[4a×3a+π(1.5a)2]
=60a2﹣12a2﹣πa2
=48a2﹣πa2;
(2)根据题意得:(a+4a+5a)(1.5a+3a+1.5a)÷(3a×4a)
=10a 6a÷12a2
=5.
.【解答】解:设t=a1+a2+…a2022,
∴M=(t﹣a2022)(t﹣a1),N=t(t﹣a1﹣a2022),
∴M﹣N=(t﹣a2022)(t﹣a1)﹣t(t﹣a1﹣a2022)=a1 a2022,
∵a1,a2022都是正数,
∴M﹣N>0,
∴M>N.
.【解答】解:(1)设A水果的进货量为xkg,则B水果的进货量为(100﹣x)kg,
采购总资金=20x+5(100﹣x)=15x+500,
∵店主准备采购的总资金不高于950元,
∴15x+500≤950,
解得x≤30,
又∵A水果的进货量(取整数)不小于28kg,
∴28≤x≤30,且x取整数,
∴x可以取28,29,30,
当x=28时,100﹣x=72,
当x=29时,100﹣x=71,
当x=30时,100﹣x=70,
∴店主有3种采购方案,
购进A水果28kg,B水果72kg,
或者购进A水果29kg,B水果71kg,
或者购进A水果30kg,B水果70kg.
(2)采购A水果akg,则采购B水果(100﹣a)kg,
采购A、B两种水果销售后所获取的利润=采购A水果销售后所获取的利润+采购B水果销售后所获取的利润
=(35﹣20) a(1﹣20%)+(6﹣5) (100﹣a)(1﹣5%)
=12a+95﹣0.95a
=11.05a+95,
在(1)的3个方案中,当购进A水果30kg时,采购A、B两种水果销售后所获取的利润最大,
最多获取利润=11.05×30+95=426.5(元),
一.选择题
.将正整数按如图所示的位置顺序排列:
根据排列规律,则2022应在( )
A.点A处 B.点B处 C.点C处 D.点D处
.某商品每次降价20%,连续两次降价后的价格为m元,则原价为( )
A.1.2m元 B.元 C.元 D.0.82m元
.一个矩形的周长为l,若矩形的长为a,则该矩形的宽为( )
A.﹣a B. C.l﹣a D.
.观察下列各数:1,,,,…,按照你发现的规律,这列数的第6个数是( )
A. B. C. D.
.下列图形都是由圆和几个黑色围棋子按一定规律组成,图①中有4个黑色棋子,图②中有7个黑色棋子,图③中有10个黑色棋子,…,依次规律,图中黑色棋子的个数是( )
A.6067 B.6066 C.6065 D.6064
.按一定规律排列的一组数据:,﹣,,﹣,,﹣,….则按此规律排列的第10个数是( )
A.﹣ B. C.﹣ D.
.观察图中正方形四个顶点所标的数字规律,可知数2022应标在( )
A.第506个正方形的右上角
B.第506个正方形的左下角
C.第505个正方形的右上角
D.第505个正方形的左下角
.(n为正整数)一定等于( )
A.an+2 B.2a2 C. D.a2n
.《孙子算经》中有一个问题:今有甲、乙、丙三人持钱.甲语乙、丙:“各将公等所持钱半以益我,钱成九十.”乙复语甲、丙:“各将公等所持钱半以益我,钱成七十.”丙复语甲、乙:“各将公等所持钱半以益我,钱成五十六.”若设甲、乙各持钱数为x、y,则丙持钱数不可以表示为( )
A. B.180﹣2x﹣y C.140﹣2x﹣y D.140﹣x﹣2y
.长为acm,宽为bcm(a>b>5)的长方形,若将长增加5cm,宽减少5cm,则它的面积会( )
A.变小 B.变大 C.不变 D.无法确定
二.填空题
.有一组单项式依次为:﹣x2,,﹣,,﹣,…,则第n个单项式是 .
.某种桔子的售价是每千克3元,用面值为100元的人民币购买了a千克,应找回 元.
.输入m,按照如图所示的程序进行计算后,输出的结果为 .(用含m的代数式表示)
.观察下列图形规律,当图形中的“〇”的个数和“.”个数差为2022时,n的值为 .
.“数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,乙稀的化学式是C2H4,丙稀的化学式是C3H6…,碳原子和氢原子的数目满足一定数学规律.设碳原子的数目为n(n为正整数,且n≥2),则这类稀的化学式可用式子 来表示.
三.解答题
.已知如图内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中,从第二个数起的数都比它上边相邻的数大n.求m,n的值.
.观察以下等式:
第1个等式:1+
第2个等式:1+
第3个等式:1+
第4个等式:1+
按照以上规律,解决下列问题:
(1)写出第5个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示),并证明.
.某居民小区为响应党的号召,开展全民健身活动,准备修建一座长方形健身广场,其设计方案及数据如图所示.已知广场内A区为长方形的成年人活动场所,B区为圆形的儿童活动场所,其余地方为绿化带.
(1)求绿化带的面积;
(2)求整座健身广场的面积是成年人活动场所面积的多少倍.
.设a1,a2,a3,…a2021,a2022都是正数,
M=(a1+a2+…a2021) (a2+a3+…a2022),
N=(a1+a2+…a2022) (a2+a3+…a2021),
试比较M、N的大小.
.某水果店主计划采购A、B两种水果100kg进行销售,其中A水果的进货量(取整数)不小于28kg,下表为这两种水果的进货价、销售价及损耗率:
项目 进货价(元/kg) 销售价(元/kg) 损耗率
A水果 20 35 20%
B水果 5 6 5%
经预算,该店主准备采购的总资金不高于950元.
(1)请你为店主设计有几种采购方案,请写出具体方案;
(2)设采购A水果akg,请用含有a字母的代数式(化简后)表示采购A、B两种水果销售后所获取的利润;在(1)方案中,最多获取利润是多少元?
参考答案与试题解析
一.选择题
.【解答】解:由题意得:在A位置的数被4除余2,在B位置的数被4除余3,在C位置的数被4整除,在D位置的数被4除余1;
2022÷4=505……2,
∴2022应在2的位置,也就是在A处.
故答案为:A.
.【解答】解:原价为:(元);
故选:B.
.【解答】解:矩形的宽为:.
故选:A.
.【解答】解:∵1=,
=,
=,
=,
…,
∴第n个数为:,
∴第6个数为:.
故选:C.
.【解答】解:∵图①中有3+1=4个黑色棋子,
图②中有3×2+1=7个黑色棋子,
图③中有3×3+1=10个黑色棋子,
…
图n中黑色棋子的个数是3n+1,
∴图2022中黑色棋子的个数是3×2022+1=6067.
故选:A.
.【解答】解:原数据可转化为:,﹣,,﹣,,﹣,…,
∴=(﹣1)1+1×,
﹣=(﹣1)2+1×,
=(﹣1)3+1×,
...
∴第n个数为:(﹣1)n+1,
∴第10个数为:(﹣1)10+1×=﹣.
故选:A.
.【解答】解:根据图形的变化可知,每四个数一个正方形,且四个数在正方形上的相对位置是相同的,
∵2022÷4=505……2,
∴2022在第506个正方形右上角位置上,
故选:A.
.【解答】解:
=(an)2
=a2n.
故选:D.
.【解答】解:设丙持钱数为z,
根据丙语得z+=56,
整理得z=56﹣,
故A选项不符合题意;
根据甲语得x+=90,
整理得z=180﹣2x﹣y,
故B选项不符合题意;
根据乙语得y+=70,
整理得z=140﹣x﹣2y,
故D选项不符合题意,C选项符合题意.
故选:C.
.【解答】解:原长方形的面积为:abcm2,
现长方形的面积为:(a+5)(b﹣5)=(ab+5b﹣5a﹣25)cm2,
因为b<a,
所以b﹣a<0,
所以ab+5b﹣5a﹣25﹣ab=5(b﹣a)﹣25<0,
即现长方形的面积小于原长方形的面积.
故选:A.
二.填空题
.【解答】解:∵﹣x2=(﹣1)1,
=(﹣1)2,
﹣=(﹣1)3,
……,
∴第n个单项式为:.
故答案为:.
.【解答】解:根据题意,a千克桔子售价为3a元,所以应找回(100﹣3a)元.
故答案为:(100﹣3a).
.【解答】解:根据题意得:(m2+8m)×2m÷m2
=m2(m+8)×2÷m2
=(m+8)×2
=2m+16.
故答案为:2m+16.
.【解答】解:∵n=1时,“ ”的个数是3=3×1;
n=2时,“ ”的个数是6=3×2;
n=3时,“ ”的个数是9=3×3;
n=4时,“ ”的个数是12=3×4;
……,
∴第n个图形中“ ”的个数是3n;
又∵n=1时,“〇”的个数是1=;
n=2时,“〇”的个数是3=,
n=3时,“〇”的个数是6=,
n=4时,“〇”的个数是10=,
……,
∴第n个“〇”的个数是,
由图形中的“〇”的个数和“.”个数差为2022,
∴①,②,
解①得:无解,
解②得:,n.
故答案为:不存在.
.【解答】解:根据题意,这类稀的化学式为 nH2n.
故答案为: nH2n.
三.解答题
.【解答】解:∵各横行中,从第二个数起的数都比它左边相邻的数大m,
∴﹣12+2m=18,
解得m=15.
又∵各竖列中,从第二个数起的数都比它上边相邻的数大n,
∴(﹣12+m)+3n=30,
将m=15代入上述方程得 3+3n=30,
解得n=9.
.【解答】解:(1)第5个等式为:,
故答案为:;
(2)猜想:第n个等式为为:,
证明:等式左边=1+
=1+
=
==右边,
故猜想成立.
故答案为:.
.【解答】解:(1)绿化带的面积:(a+4a+5a)(1.5a+3a+1.5a) ﹣[4a×3a+π(1.5a)2]
=60a2﹣12a2﹣πa2
=48a2﹣πa2;
(2)根据题意得:(a+4a+5a)(1.5a+3a+1.5a)÷(3a×4a)
=10a 6a÷12a2
=5.
.【解答】解:设t=a1+a2+…a2022,
∴M=(t﹣a2022)(t﹣a1),N=t(t﹣a1﹣a2022),
∴M﹣N=(t﹣a2022)(t﹣a1)﹣t(t﹣a1﹣a2022)=a1 a2022,
∵a1,a2022都是正数,
∴M﹣N>0,
∴M>N.
.【解答】解:(1)设A水果的进货量为xkg,则B水果的进货量为(100﹣x)kg,
采购总资金=20x+5(100﹣x)=15x+500,
∵店主准备采购的总资金不高于950元,
∴15x+500≤950,
解得x≤30,
又∵A水果的进货量(取整数)不小于28kg,
∴28≤x≤30,且x取整数,
∴x可以取28,29,30,
当x=28时,100﹣x=72,
当x=29时,100﹣x=71,
当x=30时,100﹣x=70,
∴店主有3种采购方案,
购进A水果28kg,B水果72kg,
或者购进A水果29kg,B水果71kg,
或者购进A水果30kg,B水果70kg.
(2)采购A水果akg,则采购B水果(100﹣a)kg,
采购A、B两种水果销售后所获取的利润=采购A水果销售后所获取的利润+采购B水果销售后所获取的利润
=(35﹣20) a(1﹣20%)+(6﹣5) (100﹣a)(1﹣5%)
=12a+95﹣0.95a
=11.05a+95,
在(1)的3个方案中,当购进A水果30kg时,采购A、B两种水果销售后所获取的利润最大,
最多获取利润=11.05×30+95=426.5(元),
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
