高中数学人教A版(2019)必修第二册分层练习9.2用样本估计总体B(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)必修第二册分层练习9.2用样本估计总体B(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 977.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 00:00:00 | ||
图片预览




文档简介
一、单选题
1.中国营养学会把走路称为“最简单、最优良的锻炼方式”,它不仅可以帮助减肥,还可以增强心肺功能、血管弹性、肌肉力量等.下图为甲、乙两人在同一星期内日步数的折线统计图:
则下列结论中不正确的是( )
A.这一星期内甲的日步数的中位数为11600 B.乙的日步数星期四比星期三增加了1倍以上
C.这一星期内甲的日步数的平均值大于乙 D.这一星期内甲的日步数的方差大于乙
2.高三模拟考试常常划定的总分各批次分数线,通过一定的数学模型,确定不同学科在一本、二本等各批次“学科上线有双分”的分数线.考生总成绩达到总分各批次分数线的称为总分上线;考生某一单科成绩达到及学科上线有双分的称为单科上线.学科对总分的贡献或匹配程度评价有很大的意义.利用“学科对总分上线贡献率”和“学科有效分上线命中率”这两项评价指标,来反映各学科的单科成绩对考生总分上线的贡献与匹配程度,这对有效安排备考复习计划具有十分重要的意义.某州一诊考试划定总分一本线为465分,数学一本线为104分,某班一小组的总分和数学成绩如表,则该小组“数学学科对总分上线贡献率、有效分上线命中率”分别是( )(结果保留到小数点后一位有效数字)
学生编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
数学成绩 120 117 122 101 100 112 99 111 102 100 89 98 92 84 94 113 97 104 85 85
总分成绩 495 494 493 485 483 483 482 480 479 475 471 470 463 457 454 453 448 448 441 440
A.41.7%,71.4% B.60%,71.4%
C.41.7%,35% D.60%,35%
3.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
4.下列命题是真命题的是( )
A.有甲 乙 丙三种个体按的比例分层抽样调查,如果抽取的甲个体数为,则样本容量为
B.若甲组数据的方差为,乙组数据为,,,,,则这两组数据中较稳定的是甲
C.数据,,,,,的平均数 众数 中位数相同
D.某单位 三个部门平均年龄为岁 岁和岁,又,两部门人员平均年龄为岁, 两部门人员平均年龄为岁,则该单位全体人员的平均年龄为岁
5.某个高级中学组织物理 化学学科能力竞赛,全校1000名学生都参加两科考试,考试后按学科分别评出一 二 三等奖和淘汰的这四个等级,现有某考场的两科考试数据统计如下,其中物理科目成绩为二等奖的考生有12人.如果以这个考场考生的物理和化学成绩去估计全校考生的物理和化学成绩分布,则以下说法正确的是( )
①该考场化学考试获得一等奖的有4人;
②全校物理考试获得二等奖的有240人;
③如果采用分层抽样从全校抽取200人,则化学考试被淘汰78人.
A.①②③ B.②③ C.①② D.①③
6.为比较甲,乙两名篮球运动员的近期竞技状态,选取这两名球员最近五场的得分制成如图所示的茎叶图. 有下列结论:
①甲最近五场比赛得分的中位数高于乙最近五场比赛得分的中位数;
②甲最近五场比赛得分的平均数低于乙最近五场比赛得分的平均数;
③从最近五场比赛的得分看,乙比甲更稳定;
④从最近五场比赛的得分看,甲比乙更稳定.
其中所有正确结论的序号是( )
A.②③ B.①④
C.①③ D.②④
二、多选题
7.北京时间2022年9月30日,女篮世界杯半决赛,中国队61:59澳大利亚队,时隔28年再次在半决赛中战胜澳大利亚队挺进决赛.中国队在10名上场球员中,3人得分上双.韩旭拿下全场最高的19分,10投8中,得到11个篮板和5次盖帽;队长杨力维得到18分,送出4次助攻;王思雨得到14分.根据以上信息判断,下列说法中正确的是( )
A.中国队上场的10名球员存在都有得分的可能
B.中国队上场的10名球员得分的极差不可能为17分
C.中国队上场的10名球员得分的中位数一定小于其平均数
D.3不可能是中国队上场的10名球员得分的众数
8.某高中有学生人,其中男生人,女生人,希望获得全体学生的身高信息,按照分层抽样的原则抽取了容量为的样本.经计算得到男生身高样本均值为,方差为;女生身高样本均值为,方差为.下列说法中正确的是( )
A.男生样本量为 B.每个女生入样的概率均为
C.所有样本的均值为 D.所有样本的方差为
三、填空题
9.设某组数据均落在区间内,共分为五组,对应频率分别为已知依据该组数据所绘制的频率分布直方图为轴对称图形,给出下列四个条件:
①;
②;
③;
④.
其中能确定该组数据频率分布的条件有__________.
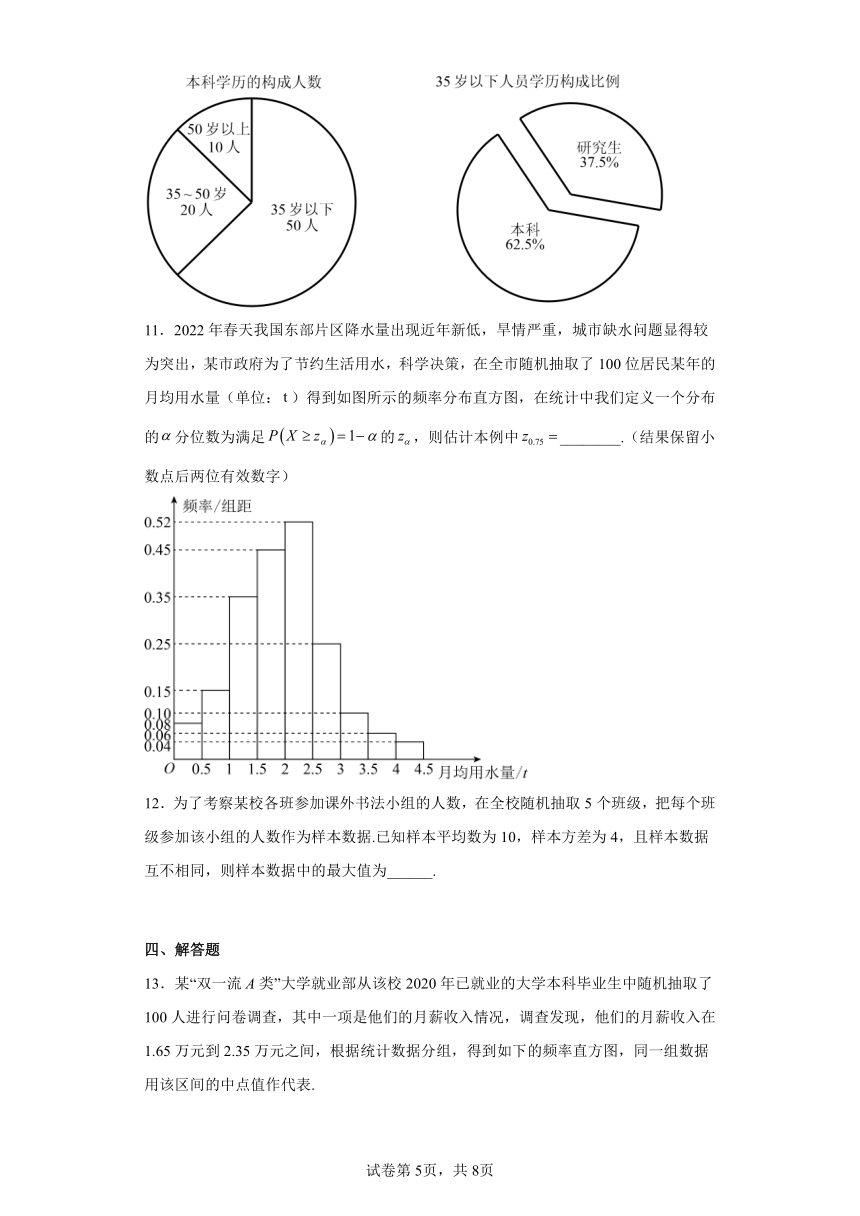
10.抽样调查某地区名教师的年龄和学历状况,情况如下饼图:则估计该地区岁以下具有研究生学历的教师人数为_______.
11.2022年春天我国东部片区降水量出现近年新低,旱情严重,城市缺水问题显得较为突出,某市政府为了节约生活用水,科学决策,在全市随机抽取了100位居民某年的月均用水量(单位:)得到如图所示的频率分布直方图,在统计中我们定义一个分布的分位数为满足的,则估计本例中________.(结果保留小数点后两位有效数字)
12.为了考察某校各班参加课外书法小组的人数,在全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据.已知样本平均数为10,样本方差为4,且样本数据互不相同,则样本数据中的最大值为______.
四、解答题
13.某“双一流A类”大学就业部从该校2020年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率直方图,同一组数据用该区间的中点值作代表.
(1)求这100人月薪收入的样本平均数和样本方差;
(2)该校在某地区就业的2018届本科毕业生共50人,决定于2019年国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设,月薪落在区间Ω左侧的每人收取400元,月薪落在区间Ω内的每人收取600元,月薪落在区间Ω右侧的每人收取800元;
方案二:按每人个月薪水的3%收取.
用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用.
参考数据:.
14.中国独有的文书工具,即笔、墨、纸、砚,有文房四宝之名,起源于南北朝时期.其中宣纸是文房四宝的一种,宣纸“始于唐代,产于泾县”,因唐代泾县隶属宣州管辖,故因地得名宣纸.宣纸按质量等级分为:正牌(优等品)、副牌(合格品)、废品三等.某公司生产的宣纸为纯手工制作,年产宣纸刀(刀张),该公司按照某种质量指标给宣纸确定等级如表所示:
的范围
质量等级 副牌 正牌 废品
在该公司所生产的宣纸中随机生产了一刀进行检验,得到频率分布直方图如图所示,已知每张正牌宣纸的利润为元,副牌宣纸利润为元,废品的利润为元.
(1)试估计该公司的年利润;
(2)市场上有一种售价为万元的机器可以改进宣纸的生产工艺,但这种机器的使用寿命为一年,只能提高宣纸的质量,不能增加宣纸的年产量;据调查这种机器生产的宣纸的质量指标如表所示:
的范围
频率
其中为质量指标x的平均值,但是由于人们对传统手工工艺的认可,改进后的正牌和副牌宣纸的利润都将下降元/张,请该公司是否购买这种机器,请你为公司提出合理建议,并说明理由.(同一组的数据用该组区间的中点值作代表)
15.某市政府为了节约生活用水,实施居民生活用水定额管理政策,即确定一个居民月用水量标准x(单位:吨),用水量不超过x的部分按平价收费,超出x的部分按议价收费,并随机抽取部分居民进行调查,抽取的居民月均用水量的频率分布直方图如图所示.(同一组中的数据以该组区间的中点值为代表)
(1)求频率分布直方图中a的值;
(2)试估计该市居民月均用水量的众数、平均数;
(3)如果希望85%的居民月均用水量不超过标准x,那么标准x定为多少比较合理?
16.2022年“中国航天日”线上启动仪式在4月24日上午举行,为普及航天知识,某校开展了“航天知识竞赛”活动,现从参加该竞赛的学生中随机抽取了60名,统计他们的成绩(满分100分),其中成绩不低于80分的学生被评为“航天达人”,将数据整理后绘制成如图所示的频率分布直方图.
(1)若该中学参加这次竞赛的共有2000名学生,试估计全校这次竞赛中“航天达人”的人数;
(2)估计参加这次竞赛的学生成绩的80%分位数;
(3)若在抽取的60名学生中,利用分层随机抽样的方法从成绩不低于70分的学生中随机抽取6人,则从成绩在[70,80),[80,90),[90,100]内的学生中分别抽取了多少人?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】对于A:直接求出中位数;
对于B:求出乙的星期三和星期四步数,计算可得;
对于C:分别计算出甲、乙平均数,即可判断;
对于D:分别计算出甲、乙方差,即可判断;
【详解】对于A:甲的步数:16000,7965,12700,2435,16800,9500,11600.从小到大排列为:2435,7965,9500,11600,12700,16000,16800.中位数是11600.故A正确;
对于B:乙的星期三步数7030,星期四步数12970.因为,所以没有增加1倍上.故B不正确;
对于C:,.
所以.故C正确;
对于D:所以.故D正确;
故选:B.
2.A
【分析】由题知,双过线人数为5人,单过线人数为7人,总分过线人数为12人,进而根据题意求解即可;
【详解】解:由图表知双过线人数为5人,单过线人数为7人,总分过线人数为12人;
“学科对总分上线贡献率”为,
“学科有效分上线命中率”为,
故选:A.
【点睛】本题考查统计的应用,考查数据分析与处理能力,是中档题.本题解题的关键在于根据已知,读懂试题,在理解的基础上,进行数据分析处理计算.
3.A
【分析】可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.
【详解】设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差可能相等可能变小,D不正确.
【点睛】本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
4.D
【分析】对于选项根据分层抽样的定义可判断正误,对于选项求出乙组数据的方程,与甲组数据的方差比较,可判断正误,对于选项求出数据的平均数、众数、中位数即可判断正误,对于选项设,,三个部门的人数为,,,根据题意可得,,从而求出该单位全体人员的平均年龄.
【详解】解:对于选项:如果抽取的甲个体数为9,则样本容量为,故选项是假命题,
对于选项:乙组数据的平均数为,方差为,
因为乙组数据的方程比甲组数据的方差小,所以这两组数据中较稳定的是乙,
故选项是假命题,
对于选项:数据1,2,3,4,4,5的平均数为、众数为4、中位数为,故选项是假命题,
对于选项:设,,三个部门的人数为,,,则有:
,化简得,
,化简得,
所以该单位全体人员的平均年龄为岁,
故选项是真命题,
故选:.
5.C
【分析】由物理二等奖的人数和频率可得该考场总共人数,乘以化学考试获得一等奖的频率可判断①;计算出全校获得物理考试二等奖的频率和总人数相乘可判断②;采用分层抽样从全校抽取200人,乘以化学考试被淘汰的人数的频率可判断③.
【详解】由于,所以该考场总共有50人,所以化学考试获得一等奖的有人,所以①正确;全校获得物理考试二等奖的有人,所以②正确;如果采用分层抽样从全校抽取200人,则化学考试被淘汰的人数为人,所以③错误.
故选:C.
6.A
【分析】根据茎叶图得到甲、乙的得分,求出中位数、平均数、方差,即可判断;
【详解】甲的得分为25,28,29,31,32;
乙的得分为28,29,30,31,32;
因为,
故甲、乙得分中位数分别为29、30;平均数分别为29、30;方差分别为、;
故正确的有②③;
故选:A
7.ABC
【分析】根据已知条件,逐项推理,即可得到选项.
【详解】61-(19+18+14)=10,中国队除3人外,剩余7人得到10分,存在10名球员存在都有得分的可能,A项正确;
中国队除3人外,剩余7人得到10分,若极差为17,则剩余7人最低得分为2分或最高得分为31分,这两种情况都不存在,即上场的10名球员得分的极差不可能为17分,B项正确;
中国队上场的10名球员得分的平均数为,按照分数从小到大排序,则8到10位分数一定是14、18、19,要使中位数大于或等于平均数,则5、6位两队员得分之和应不小于13分,这与7人得到10分不符,显然不可能,故C项正确;
根据已知条件,上场的10名球员得分情况可能为:0,0,1,1,2,3,3,14,18,19.即3可能是中国队上场的10名球员得分的众数.D项错误.
故选:ABC.
8.AC
【分析】由分层抽样可判断A;计算女生入样的概率可判断B;计算总体的均值可判断C;计算总体的方差可判断D,进而可得正确选项.
【详解】对于A:抽样比为,所以样本中男生有人,故选项A正确;
对于B:每个女生入样的概率等于抽样比,故选项B不正确;
对于C:由分层抽样知,样本中男生有人,男生有人,所有的样本均值为:,故选项C正确;
对于D:设男生分别为,,,,平均数,,女生分别为,,,,平均数,,总体的平均数为,方差为,
因为
,
而,
所以,
同理可得,
所以,
故选项D不正确;
故选:AC
9.①④
【分析】由已知对称性加下四个条件中的一个能求出,即符合题意.
【详解】已知,,
若①,则;
若②,则,不能得出;
若③,则可得,但的解不确定,
若.则,可得,,,
故答案为:①④.
【点睛】本题考查频率分布直方图的性质,本题实质就是由频率分布直方图得出,,然后判断再加哪个条件能求得各频率即可,通过解方程组可得.
10.
【分析】根据图中的数据,分别求得本科学历和研究生学历的教师人数,再根据35岁以下的本科人数所占比例求解即可得答案.
【详解】解:由图可知本科学历的教师共有人,故研究生学历的有人.
35岁以下的本科人数有人,35岁以下教师的比例为,
所以35岁以下的本科和研究生学历人数和为人,
所以35岁以下的研究生学历人数有人.
故答案为:
11.2.45
【分析】根据频率分布直方图进行数据分析,结合定义即可求得.
【详解】由题意可知:就是满足的横坐标的值,
因为对应的频率为,
对应的频率为,
对应的频率为,
对应的频率为,
对应的频率为,
所以落在内,设距离2.5的距离为,
所以,所以,所以.
故答案为:2.45
12.13
【分析】根据方差的运算公式和性质、平均数的公式,运用分类讨论思想进行求解即可.
【详解】设样本数据由小到大依次为,,,,,
记,
则,.
由于且可知,.
若,则,
得,,,中要么有1个是4其余3个是0,要么4个都是1,
这与样本数据互不相同矛盾;
若,则,取,,,满足题意;若,则,,,,只有,,,满足,但此时不满足;
若,则,,,,不满足;综上可知,,,即样本数据的最大值为13.
故答案为:13
13.(1)平均数2;方差
(2)方案一
【分析】(1)以每组的中点值代表该组的数据求解平均数,再根据公式计算方差即可;
(2)根据题意分别计算两种方案的费用,再判断即可.
【详解】(1)样本平均数(万元),
样本方差(万元2).
(2)方案一:(万元),.
月薪落在区间Ω左侧收取费用约为(万元);
月薪落在区间Ω内收取费用约为(万元);
月薪落在区间Ω右侧收取费用约为(万元).
因此这50人共收取费用约为(万元).
方案二:这50人共收取费用约为(万元).
故方案一能收到更多的费用.
14.(1)万元;(2)建议该公司购买这种机器,理由见解析.
【分析】(1)计算出一刀宣纸中正牌纸、副牌纸以及废品纸的张数,结合已知条件计算出一刀宣纸的利润的估计值,再乘以可得结果;
(2)计算出该公司改进前后一刀宣纸的利润,比较大小后可得出结论.
【详解】(1)由频率分布直方图得:一刀宣纸有正牌张,有副牌张,有废品张,
该公司一刀宣纸的利润的估计值为元,
估计该公司的年利润为万元;
(2)由频率分布直方图得:
.
这种机器生产的宣纸的质量指标如下表所示:
的范围
频率
一刀宣纸中有正牌的张数估计为,
废品的张数估计为:,
副牌的张数为:,
一刀宣纸的利润为:元,
公司改进后该公司的利润为:万元,
,建议该公司购买这种机器.
15.(1)
(2)吨,吨
(3)
【分析】(1)利用频率分布直方图中所有矩形的面积之和为1进行求解.
(2)利用频率分布直方图中的最高矩形求众数,利用每个矩形的底端中点和其面积的乘积之和来求平均数.
(3)利用频率分布直方图求85%分位数即可.
(1)
由频率分布直方图中所有矩形的面积之和为1,可得,解得.
(2)
由频率分布直方图可知,该市居民月均用水量的众数约为(吨),
由频率分布直方图可知,平均数约为(吨).
(3)
由频率分布直方图可知,月均用水量低于2.5吨的居民人数所占的百分比为,月均用水量低于3吨的居民人数所占的百分比为,
所以,由题意可得,解得.
所以如果希望85%的居民月均用水量不超过标准x,那么x定为2.9吨比较合理.
【点睛】利用频率分布直方图求解样本数据的众数、平均数、中位数,原则如下:
(1)在样本数据的频率分布直方图中,最高矩形的中点的横坐标即为该组数据的众数;
(2)在频率分布直方图中,中位数左边和右边的矩形面积相等,由此可以估计中位数的值;
(3)在频率分布直方图中,平均数等于每个小矩形的面积乘以对应小矩形底边中点的横坐标之和.
16.(1)600人;
(2)85;
(3)3人,2人,1人.
【分析】(1)根据频率分布直方图可求成绩在[80,100]内的频率,从而可求“航天达人”的人数.
(2)根据频率和可确定成绩的80%分位数在[80,90)内,根据公式可求80%分位数;
(3)根据成绩在[70,80),[80,90),[90,100]的频率比值可求各自抽取人数.
【详解】(1)由频率分布直方图可知,成绩在[80,100]内的频率为0.020×10+0.010×10=0.3,
则估计全校这次竞赛中“航天达人”的人数约为2000×0.3=600人.
(2)由频率分布直方图可知,成绩在[40,50)内的频率为0.005×10=0.05,
成绩在[50,60)内的频率为0.015×10=0.15,
成绩在[60,70)内的频率为0.020×10=0.2,
成绩在[70,80)内的频率为0.030×10=0.3,
成绩在[80,90)内的频率为0.020×10=0.2,
所以成绩在80分以下的学生所占的比例为70%,成绩在90分以下的学生所占的比例为90%,
所以成绩的80%分位数一定在[80,90)内,而,
因此估计参加这次竞赛的学生成绩的80%分位数约为85.
(3)因为,,,
所以从成绩在[70,80),[80,90),[90,100]内的学生中分别抽取了3人,2人,1人.
答案第1页,共2页
答案第1页,共2页
1.中国营养学会把走路称为“最简单、最优良的锻炼方式”,它不仅可以帮助减肥,还可以增强心肺功能、血管弹性、肌肉力量等.下图为甲、乙两人在同一星期内日步数的折线统计图:
则下列结论中不正确的是( )
A.这一星期内甲的日步数的中位数为11600 B.乙的日步数星期四比星期三增加了1倍以上
C.这一星期内甲的日步数的平均值大于乙 D.这一星期内甲的日步数的方差大于乙
2.高三模拟考试常常划定的总分各批次分数线,通过一定的数学模型,确定不同学科在一本、二本等各批次“学科上线有双分”的分数线.考生总成绩达到总分各批次分数线的称为总分上线;考生某一单科成绩达到及学科上线有双分的称为单科上线.学科对总分的贡献或匹配程度评价有很大的意义.利用“学科对总分上线贡献率”和“学科有效分上线命中率”这两项评价指标,来反映各学科的单科成绩对考生总分上线的贡献与匹配程度,这对有效安排备考复习计划具有十分重要的意义.某州一诊考试划定总分一本线为465分,数学一本线为104分,某班一小组的总分和数学成绩如表,则该小组“数学学科对总分上线贡献率、有效分上线命中率”分别是( )(结果保留到小数点后一位有效数字)
学生编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
数学成绩 120 117 122 101 100 112 99 111 102 100 89 98 92 84 94 113 97 104 85 85
总分成绩 495 494 493 485 483 483 482 480 479 475 471 470 463 457 454 453 448 448 441 440
A.41.7%,71.4% B.60%,71.4%
C.41.7%,35% D.60%,35%
3.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
4.下列命题是真命题的是( )
A.有甲 乙 丙三种个体按的比例分层抽样调查,如果抽取的甲个体数为,则样本容量为
B.若甲组数据的方差为,乙组数据为,,,,,则这两组数据中较稳定的是甲
C.数据,,,,,的平均数 众数 中位数相同
D.某单位 三个部门平均年龄为岁 岁和岁,又,两部门人员平均年龄为岁, 两部门人员平均年龄为岁,则该单位全体人员的平均年龄为岁
5.某个高级中学组织物理 化学学科能力竞赛,全校1000名学生都参加两科考试,考试后按学科分别评出一 二 三等奖和淘汰的这四个等级,现有某考场的两科考试数据统计如下,其中物理科目成绩为二等奖的考生有12人.如果以这个考场考生的物理和化学成绩去估计全校考生的物理和化学成绩分布,则以下说法正确的是( )
①该考场化学考试获得一等奖的有4人;
②全校物理考试获得二等奖的有240人;
③如果采用分层抽样从全校抽取200人,则化学考试被淘汰78人.
A.①②③ B.②③ C.①② D.①③
6.为比较甲,乙两名篮球运动员的近期竞技状态,选取这两名球员最近五场的得分制成如图所示的茎叶图. 有下列结论:
①甲最近五场比赛得分的中位数高于乙最近五场比赛得分的中位数;
②甲最近五场比赛得分的平均数低于乙最近五场比赛得分的平均数;
③从最近五场比赛的得分看,乙比甲更稳定;
④从最近五场比赛的得分看,甲比乙更稳定.
其中所有正确结论的序号是( )
A.②③ B.①④
C.①③ D.②④
二、多选题
7.北京时间2022年9月30日,女篮世界杯半决赛,中国队61:59澳大利亚队,时隔28年再次在半决赛中战胜澳大利亚队挺进决赛.中国队在10名上场球员中,3人得分上双.韩旭拿下全场最高的19分,10投8中,得到11个篮板和5次盖帽;队长杨力维得到18分,送出4次助攻;王思雨得到14分.根据以上信息判断,下列说法中正确的是( )
A.中国队上场的10名球员存在都有得分的可能
B.中国队上场的10名球员得分的极差不可能为17分
C.中国队上场的10名球员得分的中位数一定小于其平均数
D.3不可能是中国队上场的10名球员得分的众数
8.某高中有学生人,其中男生人,女生人,希望获得全体学生的身高信息,按照分层抽样的原则抽取了容量为的样本.经计算得到男生身高样本均值为,方差为;女生身高样本均值为,方差为.下列说法中正确的是( )
A.男生样本量为 B.每个女生入样的概率均为
C.所有样本的均值为 D.所有样本的方差为
三、填空题
9.设某组数据均落在区间内,共分为五组,对应频率分别为已知依据该组数据所绘制的频率分布直方图为轴对称图形,给出下列四个条件:
①;
②;
③;
④.
其中能确定该组数据频率分布的条件有__________.
10.抽样调查某地区名教师的年龄和学历状况,情况如下饼图:则估计该地区岁以下具有研究生学历的教师人数为_______.
11.2022年春天我国东部片区降水量出现近年新低,旱情严重,城市缺水问题显得较为突出,某市政府为了节约生活用水,科学决策,在全市随机抽取了100位居民某年的月均用水量(单位:)得到如图所示的频率分布直方图,在统计中我们定义一个分布的分位数为满足的,则估计本例中________.(结果保留小数点后两位有效数字)
12.为了考察某校各班参加课外书法小组的人数,在全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据.已知样本平均数为10,样本方差为4,且样本数据互不相同,则样本数据中的最大值为______.
四、解答题
13.某“双一流A类”大学就业部从该校2020年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率直方图,同一组数据用该区间的中点值作代表.
(1)求这100人月薪收入的样本平均数和样本方差;
(2)该校在某地区就业的2018届本科毕业生共50人,决定于2019年国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设,月薪落在区间Ω左侧的每人收取400元,月薪落在区间Ω内的每人收取600元,月薪落在区间Ω右侧的每人收取800元;
方案二:按每人个月薪水的3%收取.
用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用.
参考数据:.
14.中国独有的文书工具,即笔、墨、纸、砚,有文房四宝之名,起源于南北朝时期.其中宣纸是文房四宝的一种,宣纸“始于唐代,产于泾县”,因唐代泾县隶属宣州管辖,故因地得名宣纸.宣纸按质量等级分为:正牌(优等品)、副牌(合格品)、废品三等.某公司生产的宣纸为纯手工制作,年产宣纸刀(刀张),该公司按照某种质量指标给宣纸确定等级如表所示:
的范围
质量等级 副牌 正牌 废品
在该公司所生产的宣纸中随机生产了一刀进行检验,得到频率分布直方图如图所示,已知每张正牌宣纸的利润为元,副牌宣纸利润为元,废品的利润为元.
(1)试估计该公司的年利润;
(2)市场上有一种售价为万元的机器可以改进宣纸的生产工艺,但这种机器的使用寿命为一年,只能提高宣纸的质量,不能增加宣纸的年产量;据调查这种机器生产的宣纸的质量指标如表所示:
的范围
频率
其中为质量指标x的平均值,但是由于人们对传统手工工艺的认可,改进后的正牌和副牌宣纸的利润都将下降元/张,请该公司是否购买这种机器,请你为公司提出合理建议,并说明理由.(同一组的数据用该组区间的中点值作代表)
15.某市政府为了节约生活用水,实施居民生活用水定额管理政策,即确定一个居民月用水量标准x(单位:吨),用水量不超过x的部分按平价收费,超出x的部分按议价收费,并随机抽取部分居民进行调查,抽取的居民月均用水量的频率分布直方图如图所示.(同一组中的数据以该组区间的中点值为代表)
(1)求频率分布直方图中a的值;
(2)试估计该市居民月均用水量的众数、平均数;
(3)如果希望85%的居民月均用水量不超过标准x,那么标准x定为多少比较合理?
16.2022年“中国航天日”线上启动仪式在4月24日上午举行,为普及航天知识,某校开展了“航天知识竞赛”活动,现从参加该竞赛的学生中随机抽取了60名,统计他们的成绩(满分100分),其中成绩不低于80分的学生被评为“航天达人”,将数据整理后绘制成如图所示的频率分布直方图.
(1)若该中学参加这次竞赛的共有2000名学生,试估计全校这次竞赛中“航天达人”的人数;
(2)估计参加这次竞赛的学生成绩的80%分位数;
(3)若在抽取的60名学生中,利用分层随机抽样的方法从成绩不低于70分的学生中随机抽取6人,则从成绩在[70,80),[80,90),[90,100]内的学生中分别抽取了多少人?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】对于A:直接求出中位数;
对于B:求出乙的星期三和星期四步数,计算可得;
对于C:分别计算出甲、乙平均数,即可判断;
对于D:分别计算出甲、乙方差,即可判断;
【详解】对于A:甲的步数:16000,7965,12700,2435,16800,9500,11600.从小到大排列为:2435,7965,9500,11600,12700,16000,16800.中位数是11600.故A正确;
对于B:乙的星期三步数7030,星期四步数12970.因为,所以没有增加1倍上.故B不正确;
对于C:,.
所以.故C正确;
对于D:所以.故D正确;
故选:B.
2.A
【分析】由题知,双过线人数为5人,单过线人数为7人,总分过线人数为12人,进而根据题意求解即可;
【详解】解:由图表知双过线人数为5人,单过线人数为7人,总分过线人数为12人;
“学科对总分上线贡献率”为,
“学科有效分上线命中率”为,
故选:A.
【点睛】本题考查统计的应用,考查数据分析与处理能力,是中档题.本题解题的关键在于根据已知,读懂试题,在理解的基础上,进行数据分析处理计算.
3.A
【分析】可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.
【详解】设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差可能相等可能变小,D不正确.
【点睛】本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
4.D
【分析】对于选项根据分层抽样的定义可判断正误,对于选项求出乙组数据的方程,与甲组数据的方差比较,可判断正误,对于选项求出数据的平均数、众数、中位数即可判断正误,对于选项设,,三个部门的人数为,,,根据题意可得,,从而求出该单位全体人员的平均年龄.
【详解】解:对于选项:如果抽取的甲个体数为9,则样本容量为,故选项是假命题,
对于选项:乙组数据的平均数为,方差为,
因为乙组数据的方程比甲组数据的方差小,所以这两组数据中较稳定的是乙,
故选项是假命题,
对于选项:数据1,2,3,4,4,5的平均数为、众数为4、中位数为,故选项是假命题,
对于选项:设,,三个部门的人数为,,,则有:
,化简得,
,化简得,
所以该单位全体人员的平均年龄为岁,
故选项是真命题,
故选:.
5.C
【分析】由物理二等奖的人数和频率可得该考场总共人数,乘以化学考试获得一等奖的频率可判断①;计算出全校获得物理考试二等奖的频率和总人数相乘可判断②;采用分层抽样从全校抽取200人,乘以化学考试被淘汰的人数的频率可判断③.
【详解】由于,所以该考场总共有50人,所以化学考试获得一等奖的有人,所以①正确;全校获得物理考试二等奖的有人,所以②正确;如果采用分层抽样从全校抽取200人,则化学考试被淘汰的人数为人,所以③错误.
故选:C.
6.A
【分析】根据茎叶图得到甲、乙的得分,求出中位数、平均数、方差,即可判断;
【详解】甲的得分为25,28,29,31,32;
乙的得分为28,29,30,31,32;
因为,
故甲、乙得分中位数分别为29、30;平均数分别为29、30;方差分别为、;
故正确的有②③;
故选:A
7.ABC
【分析】根据已知条件,逐项推理,即可得到选项.
【详解】61-(19+18+14)=10,中国队除3人外,剩余7人得到10分,存在10名球员存在都有得分的可能,A项正确;
中国队除3人外,剩余7人得到10分,若极差为17,则剩余7人最低得分为2分或最高得分为31分,这两种情况都不存在,即上场的10名球员得分的极差不可能为17分,B项正确;
中国队上场的10名球员得分的平均数为,按照分数从小到大排序,则8到10位分数一定是14、18、19,要使中位数大于或等于平均数,则5、6位两队员得分之和应不小于13分,这与7人得到10分不符,显然不可能,故C项正确;
根据已知条件,上场的10名球员得分情况可能为:0,0,1,1,2,3,3,14,18,19.即3可能是中国队上场的10名球员得分的众数.D项错误.
故选:ABC.
8.AC
【分析】由分层抽样可判断A;计算女生入样的概率可判断B;计算总体的均值可判断C;计算总体的方差可判断D,进而可得正确选项.
【详解】对于A:抽样比为,所以样本中男生有人,故选项A正确;
对于B:每个女生入样的概率等于抽样比,故选项B不正确;
对于C:由分层抽样知,样本中男生有人,男生有人,所有的样本均值为:,故选项C正确;
对于D:设男生分别为,,,,平均数,,女生分别为,,,,平均数,,总体的平均数为,方差为,
因为
,
而,
所以,
同理可得,
所以,
故选项D不正确;
故选:AC
9.①④
【分析】由已知对称性加下四个条件中的一个能求出,即符合题意.
【详解】已知,,
若①,则;
若②,则,不能得出;
若③,则可得,但的解不确定,
若.则,可得,,,
故答案为:①④.
【点睛】本题考查频率分布直方图的性质,本题实质就是由频率分布直方图得出,,然后判断再加哪个条件能求得各频率即可,通过解方程组可得.
10.
【分析】根据图中的数据,分别求得本科学历和研究生学历的教师人数,再根据35岁以下的本科人数所占比例求解即可得答案.
【详解】解:由图可知本科学历的教师共有人,故研究生学历的有人.
35岁以下的本科人数有人,35岁以下教师的比例为,
所以35岁以下的本科和研究生学历人数和为人,
所以35岁以下的研究生学历人数有人.
故答案为:
11.2.45
【分析】根据频率分布直方图进行数据分析,结合定义即可求得.
【详解】由题意可知:就是满足的横坐标的值,
因为对应的频率为,
对应的频率为,
对应的频率为,
对应的频率为,
对应的频率为,
所以落在内,设距离2.5的距离为,
所以,所以,所以.
故答案为:2.45
12.13
【分析】根据方差的运算公式和性质、平均数的公式,运用分类讨论思想进行求解即可.
【详解】设样本数据由小到大依次为,,,,,
记,
则,.
由于且可知,.
若,则,
得,,,中要么有1个是4其余3个是0,要么4个都是1,
这与样本数据互不相同矛盾;
若,则,取,,,满足题意;若,则,,,,只有,,,满足,但此时不满足;
若,则,,,,不满足;综上可知,,,即样本数据的最大值为13.
故答案为:13
13.(1)平均数2;方差
(2)方案一
【分析】(1)以每组的中点值代表该组的数据求解平均数,再根据公式计算方差即可;
(2)根据题意分别计算两种方案的费用,再判断即可.
【详解】(1)样本平均数(万元),
样本方差(万元2).
(2)方案一:(万元),.
月薪落在区间Ω左侧收取费用约为(万元);
月薪落在区间Ω内收取费用约为(万元);
月薪落在区间Ω右侧收取费用约为(万元).
因此这50人共收取费用约为(万元).
方案二:这50人共收取费用约为(万元).
故方案一能收到更多的费用.
14.(1)万元;(2)建议该公司购买这种机器,理由见解析.
【分析】(1)计算出一刀宣纸中正牌纸、副牌纸以及废品纸的张数,结合已知条件计算出一刀宣纸的利润的估计值,再乘以可得结果;
(2)计算出该公司改进前后一刀宣纸的利润,比较大小后可得出结论.
【详解】(1)由频率分布直方图得:一刀宣纸有正牌张,有副牌张,有废品张,
该公司一刀宣纸的利润的估计值为元,
估计该公司的年利润为万元;
(2)由频率分布直方图得:
.
这种机器生产的宣纸的质量指标如下表所示:
的范围
频率
一刀宣纸中有正牌的张数估计为,
废品的张数估计为:,
副牌的张数为:,
一刀宣纸的利润为:元,
公司改进后该公司的利润为:万元,
,建议该公司购买这种机器.
15.(1)
(2)吨,吨
(3)
【分析】(1)利用频率分布直方图中所有矩形的面积之和为1进行求解.
(2)利用频率分布直方图中的最高矩形求众数,利用每个矩形的底端中点和其面积的乘积之和来求平均数.
(3)利用频率分布直方图求85%分位数即可.
(1)
由频率分布直方图中所有矩形的面积之和为1,可得,解得.
(2)
由频率分布直方图可知,该市居民月均用水量的众数约为(吨),
由频率分布直方图可知,平均数约为(吨).
(3)
由频率分布直方图可知,月均用水量低于2.5吨的居民人数所占的百分比为,月均用水量低于3吨的居民人数所占的百分比为,
所以,由题意可得,解得.
所以如果希望85%的居民月均用水量不超过标准x,那么x定为2.9吨比较合理.
【点睛】利用频率分布直方图求解样本数据的众数、平均数、中位数,原则如下:
(1)在样本数据的频率分布直方图中,最高矩形的中点的横坐标即为该组数据的众数;
(2)在频率分布直方图中,中位数左边和右边的矩形面积相等,由此可以估计中位数的值;
(3)在频率分布直方图中,平均数等于每个小矩形的面积乘以对应小矩形底边中点的横坐标之和.
16.(1)600人;
(2)85;
(3)3人,2人,1人.
【分析】(1)根据频率分布直方图可求成绩在[80,100]内的频率,从而可求“航天达人”的人数.
(2)根据频率和可确定成绩的80%分位数在[80,90)内,根据公式可求80%分位数;
(3)根据成绩在[70,80),[80,90),[90,100]的频率比值可求各自抽取人数.
【详解】(1)由频率分布直方图可知,成绩在[80,100]内的频率为0.020×10+0.010×10=0.3,
则估计全校这次竞赛中“航天达人”的人数约为2000×0.3=600人.
(2)由频率分布直方图可知,成绩在[40,50)内的频率为0.005×10=0.05,
成绩在[50,60)内的频率为0.015×10=0.15,
成绩在[60,70)内的频率为0.020×10=0.2,
成绩在[70,80)内的频率为0.030×10=0.3,
成绩在[80,90)内的频率为0.020×10=0.2,
所以成绩在80分以下的学生所占的比例为70%,成绩在90分以下的学生所占的比例为90%,
所以成绩的80%分位数一定在[80,90)内,而,
因此估计参加这次竞赛的学生成绩的80%分位数约为85.
(3)因为,,,
所以从成绩在[70,80),[80,90),[90,100]内的学生中分别抽取了3人,2人,1人.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
