高中数学人教A版(2019)必修第二册分层练习8..6空间直线、平面的垂直C(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)必修第二册分层练习8..6空间直线、平面的垂直C(含答案) | 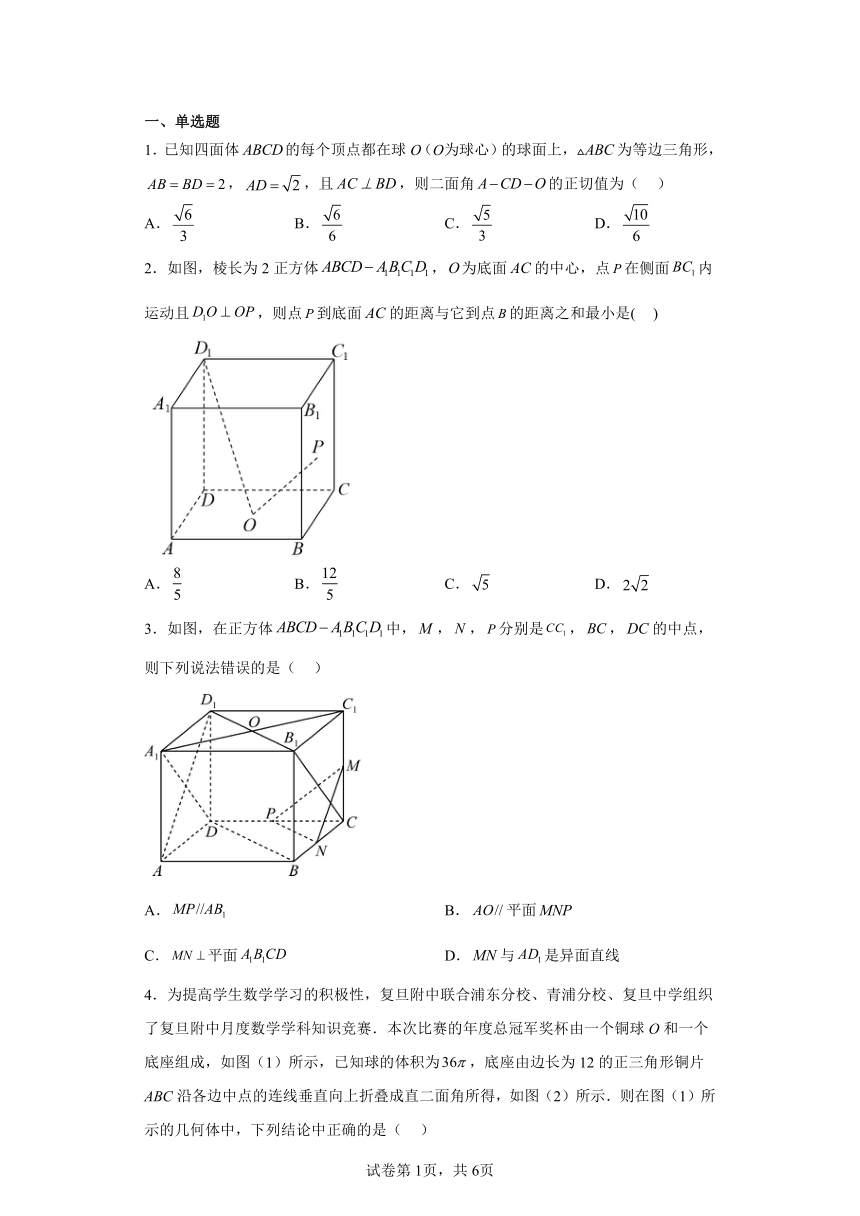 | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 19:05:31 | ||
图片预览





文档简介
一、单选题
1.已知四面体的每个顶点都在球O(О为球心)的球面上,为等边三角形,,,且,则二面角的正切值为( )
A. B. C. D.
2.如图,棱长为2正方体,为底面的中心,点在侧面内运动且,则点到底面的距离与它到点的距离之和最小是( )
A. B. C. D.
3.如图,在正方体中,,,分别是,,的中点,则下列说法错误的是( )
A. B.平面
C.平面 D.与是异面直线
4.为提高学生数学学习的积极性,复旦附中联合浦东分校、青浦分校、复旦中学组织了复旦附中月度数学学科知识竞赛.本次比赛的年度总冠军奖杯由一个铜球O和一个底座组成,如图(1)所示,已知球的体积为,底座由边长为12的正三角形铜片ABC沿各边中点的连线垂直向上折叠成直二面角所得,如图(2)所示.则在图(1)所示的几何体中,下列结论中正确的是( )
A.CD与BE是异面直线
B.异面直线AB与CD所成角的大小为45°
C.由A、B、C三点确定的平面截球所得的截面面积为
D.球面上的点到底座底面DEF的最大距离为
5.如图,矩形中,,为边的中点.将沿直线翻折成(平面).若在线段上(点与,不重合),则在翻折过程中,给出下列判断:
①当为线段中点时,为定值;
②存在某个位置,使;
③当四棱锥体积最大时,点到平面的距离为;
④当二面角的大小为时,异面直线与所成角的余弦值为.
其中判断正确的个数为( )
A.1 B.2 C.3 D.4
6.如图所示,在正方体中,过对角线的一个平面交于E,交于F,给出下面几个命题:
①四边形一定是平行四边形;
②四边形有可能是正方形;
③平面有可能垂直于平面;
④设与DC的延长线交于M,与DA的延长线交于N,则M N B三点共线;
⑤四棱锥的体积为定值.
以上命题中真命题的个数为( )
A.2 B.3 C.4 D.5
二、多选题
7.如图,正方体棱长为1,P是上的一个动点,下列结论中正确的是( )
A.的最小值为
B.的最小值为
C.当P在直线上运动时,三棱锥的体积不变
D.以点B为球心,为半径的球面与面的交线长为
8.已知正方体的棱长为2,动点F在正方形内,则( )
A.若平面,则点F的位置唯一
B.若平面,则不可能垂直
C.若,则三棱锥的外接球表面积为
D.若点E为BC中点,则三棱锥的体积是三棱锥体积的一半
三、填空题
9.三棱锥体积为,且,则三棱锥外接球的表面积为____________.
10.已知正方体的棱长为2,M,N分别是的中点,点P是截面(包括边界)上的动点,,则与平面所成最大角的正切值为_______.
11.如图,在正方体,中,E,F,G分别为棱上的点(与正方体顶点不重合),过作平面,垂足为H.设正方体的棱长为1,给出以下四个结论:
①若E,F,G分别是的中点,则;
②若E,F,G分别是的中点,则用平行于平面的平面去截正方体,得到的截面图形一定是等边三角形;
③可能为直角三角形;
④.
其中所有正确结论的序号是________.
12.四棱锥A﹣BCDE的各顶点都在同一球面上,AB⊥底面BCDE,底面BCDE为梯形,∠BCD=60°,且AB=CB=BE=ED=2,则此球的表面积等于_________.
四、解答题
13.如图,在四棱锥中,是正三角形,四边形是菱形,,,点是的中点.
(1)求证:平面;
(2)若平面平面,求点到平面的距离.
14.已知正方体的棱长为a,E F分别为棱 的中点,P为体对角线所在直线上一动点.
(1)作出该正方体过点E F且和直线垂直的截面,并证明该截面和直线垂直;
(2)求出△EFP绕直线EF旋转而成的几何体体积的最小值;
(3)若动点M在直线EF上运动,动点N在平面上运动,求的最小值.
15.七面体玩具是一种常见的儿童玩具.在几何学中,七面体是指由七个面组成的多面体,常见的七面体有六角锥 五角柱 正三角锥柱 Szilassi多面体等.在拓扑学中,共有34种拓扑结构明显差异的凸七面体,它们可以看作是由一个长方体经过简单切割而得到的.在如图所示的七面体中,平面
(1)在该七面体中,探究以下两个结论是否正确.若正确,给出证明;若不正确,请说明理由:
①平面;
②平面;
(2)求该七面体的体积.
16.如图,三棱柱中,侧面为菱形,的中点为,且平面.
(1)证明:;
(2)若,,,求三棱柱的高;
(3)在(2)的条件下,求三棱柱的表面积.
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.A
【分析】若为中点,连接,利用线面垂直的判定、勾股定理及面面垂直判定可得面面,结合已知条件有△为等腰直角三角形,进而可确定四面体外接球球心的位置,若为中点,连接,易知即为二面角的平面角,即可求其正切值.
【详解】若为中点,连接,由为等边三角形,则,又,且,
∴面,又面,即,
由题设,,,而,
∴,即,又,面,
∴面,而面,则面面,
由上可得:,则,故△为等腰直角三角形,
∴综上,四面体的球心为△的中心,即靠近的三等分点,
若为中点,连接,易知:即为二面角的平面角,
由上、且,面,可得面,
又面,则,即,
∴,而,
∴.
故选:A.
【点睛】关键点点睛:根据线线垂直、勾股定理,结合线面、面面垂直的判定证面面且△为等腰直角三角形,即可确定四面体球心的位置,再由二面角的定义找到其平面角,最后由已知条件求其正切值即可.
2.A
【分析】取中点,连接,证明平面,求出P在FC上.将平面沿BC翻折到与平面ABCD共面,将B关于CF对称到,过作与E,则即为点到底面的距离与它到点的距离之和的最小值.
【详解】取中点,连接,
由,,可知,则,
∴由知,即.
∵平面ABCD,⊥平面ABCD,∴AC⊥,又AC⊥BD,BD∩=B,
∴平面,∵平面,∴,
∵,∴平面,
∵,∴平面,平面,
∵在侧面内,∴平面平面,即P在CF上;
∵平面⊥平面ABCD,且交线为BC,
∴P到平面ABCD的距离即为P到BC的距离,
将平面沿BC翻折到与平面ABCD共面,如图:
将B关于CF对称到,过作与E,则即为点到底面的距离与它到点的距离之和的最小值.
以B为原点,建立如图所示坐标系,则B(0,0),F(1,0),C(0,2),
直线CF方程为,即,
设,则,
∴.
故选:A﹒
3.D
【分析】根据所给条件和线面关系,逐项分析判断即可得解.
【详解】
对A,如图所示,连接,
因为点为中点,
所以,在正方体中易得,
所以,故A正确;
对B,如图所示,连接交于点,
连接,与交于点,连接,
在正方体中,易得,,
所以四边形为平行四边形,
则,又为中点,
点在上,则易知点为的中心点,
因为点为中点,所以,
又平面,平面,
所以平面,故B正确;
对C,如图所示,连接,
在正方体中,易知,
所以平面,又平面,
所以,
又为,中点,
则,又,所以,
所以平面,故C正确;
对D,如图所示,连接,
易知:又,
则,所以与共面,故D错误.
故选:D
4.C
【分析】取中点N,M,利用给定条件证明,推理判断A,B;求出外接圆半径,结合球面截面圆性质计算判断C,D作答.
【详解】取中点N,M,连接,如图,
因为正三角形,则,而平面平面,平面平面,平面,
于是得平面,同理平面,即,,
因此,四边形是平行四边形,有,则直线CD与BE在同一平面内,A不正确;
由选项A,同理可得,则异面直线AB与CD所成角等于直线DF与CD所成角,B不正确;
由选项A知,,同理可得,正外接圆半径,
由A、B、C三点确定的平面截球所得的截面圆是的外接圆,此截面面积为,C正确;
体积为的球半径,由得,由选项C知,球心到平面的距离,
由选项A,同理可得点A到平面的距离为,即平面与平面的距离为,
所以球面上的点到底座底面DEF的最大距离为,D不正确.
故选:C
【点睛】易错点睛:异面直线所成的角的取值范围是,当求出角的余弦值为负时,要取其相反数作为异面直线夹角余弦.
5.B
【分析】①利用余弦定理判断;②用线线垂直判断;③由垂线段判断;④由二面角与线线角公式判断.
【详解】在矩形 中, , 不妨令 2, 则:
(1)取DC的中点 , 连接 ,
易知 且为定值,
(定值)
所以MB的长为定值, 故①正确;
(2)假设存在某个位置, 使 , 连接 , 取DE的中点 , 连接 ,
显然 , 而 平面 ,
平面 ,
进而有 , 但 , 不可能相等,
所以不可能有 , 故②错误;
(3)由题意得, 是等腰直角三角形, 到 的距离是 ,
当平面 平面 时, 四棱雉 DE体积最大,
点 到平面 的距离为 , 故③正确;
(4)易知二面角 的平面角 , 当二面角 的大小为 时,
又 , 所以 ,
又易知异面直线 与 所成角为 ,
故④错误,
综上可知, 正确的有2个.
故选: B.
6.C
【分析】由面面平行的性质和四边形的判定定理可判断①;由正方形的性质可判断②;由面面垂直的判定定理可判断③;由两平面相交的性质可判断④;由等积法和棱锥的体积公式可判断⑤.
【详解】因为平面与平面平行,截面与它们交于,BF,可得,
同样可得,所以四边形是一个平行四边形,故①正确;
如果四边形是正方形,则,
因为,所以平面,
又平面,E与A重合,此时不是正方形,故②错误;
当两条棱上的交点是中点时,四边形为菱形,平面,
此时四边形垂直于平面,故③正确;
由与DC的延长线交于M,可得,且,
又因为平面,平面ABCD,
所以平面,平面ABCD,
又因为平面,平面ABCD,
所以平面平面,
同理平面平面,
所以BM,BN都是平面与平面ABCD的交线,
所以B,M,N三点共线,故④正确;
由于,平面,
则E,F到平面的距离相等,且为正方体的棱长,三角形的面积为定值,
所以四棱锥的体积为定值,故⑤正确.
故选:C.
【点睛】此题涉及的设问情况较多,有一定成立,有可能成立.对于一定成立的命题,需要利用定理加以证明,对于可能成立的问题举出例子即可说明其成立,利用反证法才能证明其不成立.故此类题在判断时,要学会选用适当的方法.
7.BCD
【分析】当时,BP最小,结合正三角形性质,求得B到直线的距离判断A,将平面翻折到平面上,求得PA+PC的最小值判断B,由题可得平面,进而可得三棱锥的体积不变,判断C,根据球的截面的性质可得以点B为球心,为半径的球面与面 的交线即为的内切圆,即可判断D.
【详解】对于A,当时,BP最小,由于
到直线的距离,故A错误;
对于B,将平面翻折到平面上,如图,
连接AC,与的交点即为点P,此时取最小值AC,
在三角形ADC中,,,故B正确;
对于C,由正方体的性质可得,平面,
平面,到平面的距离为定值,
又为定值,则为定值,即三棱锥的体积不变,故正确;
对于D,由于平面,设与平面交于点,
,设以为球心,为半径的球与面交线上任一点为,
,,
在以为圆心,为半径的圆上,
由于为正三角形,边长为 ,其内切圆半径为 ,
故此圆恰好为的内切圆,完全落在面内,
交线长为,故正确.
故选:BCD.
8.AD
【分析】求得点F的坐标判断选项A;求得同时满足两个条件的点F的坐标判断选项B;求得三棱锥的外接球表面积判断选项C;求得三棱锥的体积和三棱锥体积判断选项D.
【详解】如图,以D为原点分别以DA、DC、为x轴、y轴、z轴建立空间直角坐标系:
则,,,,,,,,
由于动点F在正方形内,可设,其中,,
选项A:若平面,则,.
由于,,,
则,解得:或(舍去),
此时,即点F的位置唯一,故选项A正确;
选项B:,,
设平面的一个法向量为.则,
令,得,,故,
而,若平面,则,
则,即,
所以,此时,
而,所以,
当时,,此时,则.故选项B不正确;
选项C:由于,则F为的中点,此时,
设三棱锥的的外接球的球心为,则,
即,解得:,
所以,则三棱锥的的外接球的半径为,
所以三棱锥的的外接球表面积为,
故选项C不正确;
选项D:点E为BC中点,由正方体可知平面,
则
则三棱锥的体积是三棱锥体积的一半. 故选项D正确.
故选:AD
9.
【分析】取BC中点D,连PD,连AD并延长至O1,使DO1=AD,连接BO1,CO1,PO1,
由条件证得O1是外接圆圆心及PO1⊥平面ABC,再判断外接球球心O位置经推理计算即可得解.
【详解】三棱锥中,取BC中点D,连PD,连AD并延长至O1,使DO1=AD,连接BO1,CO1,PO1,如图:
于是得四边形为平行四边形,而,是菱形,
在中,,由余弦定理有,即,
则,是正三角形,,于是得O1是外接圆圆心,
因,D为BC中点,则PD⊥BC,又AO1⊥BC,,平面,从而有平面,,
同理,而,从而得平面,由球的截面小圆性质知,三棱锥外接球球心O在直线上,
又,则,解得,
设球O的半径为R,则,,中,,即,解得,
则球O的表面积为,
所以三棱锥外接球的表面积为.
故答案为:
10.
【分析】先分析得到点P的轨迹是圆,然后将与平面所成最大角的正切值转化为求的最大正切值并计算即可.
【详解】取的中点O,连接,由正方体性质可知平面,则,即如下图(2),点P的轨迹是,半径为,又M到平面的距离为,因为,所E到的距离为,则为直线与平面的夹角,当O,T,P共线时,则此时最小,的值最大,,所以,
即.
故答案为:.
11.①④
【分析】①等体积法判断;②根据正方体的性质画出平行于平面的可能截面情况;③由正方体性质,通过定两点,移动另一点判断的内角变化趋势即可;④设,利用等体积法,结合正余弦定理、三角形面积公式、锥体体积公式化简即可判断.
【详解】①由,而,
所以,可得,正确;
②根据正方体的性质平行平面的平面有如下情况:
当截面在面与面之间时为六边形,在面左上或面右下时为等边三角形,错误;
③分别在上不为顶点任意点,当从到过程递减,即小于,同理知:也小于,不可能为直角三角形,错误;
④若,又,即,
所以,
则,即,
所以,即,正确;
故答案为:①④
【点睛】关键点点睛:①④应用等体积法计算或转化,②由正方体性质及平面的基本性质作出截面判断;③根据正方体的性质,动点分析三角形的内角变化趋势.
12.
【分析】由条件确定球心位置及球的半径,由此计算球的表面积.
【详解】若,又,则四边形BCDE为平行四边形,与条件矛盾,
∴ ,又CB=BE=ED=2,∠BCD=60°,
∴ CD=4,
∴ ,
∴是以CD为斜边的直角三角形,同理可得为CD为斜边的直角三角形,
∴ 四边形BCDE的外接圆圆心为CD的中点,记CD中点为,
设四棱锥A﹣BCDE的外接球的球心为O,则平面BCDE,
又AB⊥底面BCDE,
∴ ,设,设球的半径为R,过点O作,垂足为F,
∵ ,
∴ ,
∴ ,
∴ 球的半径,
∴ 球的表面积,
故答案为:.
【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.
13.(1)证明见解析;(2).
【分析】(1)连接交于,利用中位线易得∥,进而利用线面平行的判定定理即可证明;
(2)取中点,利用面面垂直得平面,从而可求得,利用等体积法即可求解点到平面的距离.
【详解】(1)在四棱锥S ABCD中,连接交于,则为中点,连接,又为中点,∴,又平面,平面,∴平面.
(2)∵四边形是菱形,且,∴为正三角形,取中点的,连接,,则,∵平面平面,平面平面,∴平面,
∵均是正三角形,AB=2,易得, ,
∴.
易得,由,∴,
取的中点,连接,因为,∴,
∴,可得,
设点到平面的距离为,∴,
解得,即点到平面的距离为.
14.(1)见解析;
(2);
(3)a.
【分析】(1)取DD1中点为G,连接FG、EG,则⊥平面EFG.
(2)由(1)知⊥平面EFG,设,
由图可知此时△EFP的高为PH,且此时△EFP的高最短,△EFP绕EF旋转成的几何体体积最小,该几何体为两个相同的圆锥的组合体,圆锥底面半径为PH,高为EH.
(3)P在上,在平面投影为在平面上的投影为,则要使|PM|+|PN|最小,M点为EF中点,N点上,且有PN⊥.
将平面沿翻折到平面内,作M点关于的对称点,则过作N⊥与N,N即为|PM|+|PN|的最小值.
【详解】(1)如图,取DD1中点为G,连接FG、EG,则⊥平面EFG.
证明如下:设EF和交点为H,连接GH,
∴GH⊥.
连接,则⊥,又由⊥平面知,
故⊥平面,∴⊥,
∵E F分别为棱 的中点,∴,∴EF⊥,
又GHEF=H,GH和EF平面EFG,∴⊥平面EFG.
(2)由(1)知⊥平面EFG,设,
由图可知此时△EFP的高为PH,且此时△EFP的高最短,△EFP绕EF旋转成的几何体体积最小,该几何体为两个相同的圆锥的组合体,圆锥底面半径为PH,高为EH.
|EH|=|EF|=,
在△BDD1中,,
在△中,,
,
,
形成的几何体的体积为.
(3)P在上,在平面投影为在平面上的投影为,
则要使|PM|+|PN|最小,M点为EF中点,N点上,且有PN⊥.
将平面沿翻折到平面内,如图所示,作M点关于的对称点,则过作N⊥与N,N即为|PM|+|PN|的最小值.
∵,
,
,
,
∥,
∵∥,
∴四边形为平行四边形,
.
即|PM|+|PN|最小值为a.
15.(1)结论①正确;证明见解析;结论②错误;答案见解析;(2).
【分析】(1)①由平行四边形得线线平行,再得线面平行;
②假设平面,平面,得平面,得,
但,所以,与矛盾,故②错误.
(2)将七面体进行分解,
七面体的体积等于,转化为容易求体积的几何体来计算;
也可补形为长方体,通过来求解;
以及利用空间直角坐标系也行.
【详解】(1)结论①正确,结论②错误,理由如下:
对于结论①,因为且,连接,
所以四边形是平行四边形,
所以,因为平面,平面,
平面结论①正确
对于结论②,若,则,
因为平面,,所以平面,
所以,又因为,所以平面,
所以,而在梯形中,,
,所以,与矛盾
所以结论②错误.
(2)方法一:连接,交于点,连接,
则在平面中,与EG相交,
设交点为,则由可得,
又,
该七面体的体积等于
方法二:将该七面体补成如图所示的长方体;
方法三:建立空间直角坐标系,利用空间向量求点到平面的距离
后求三棱锥的体积.(参照给分
【点睛】充分利用题目信息,特别是几何体的几何特征,并会假设结论成立,推导,若得出矛盾,则假设错误,否则假设成立.复杂的不规则的几何体体积求解,需要转化为常见几何体的体积来解.
16.(1)证明见解析
(2)
(3)
【分析】(1)要证,即证平面,由菱形的对角线垂直和线面垂直的性质即可得证.
(2) 要求三菱柱的高,根据题中已知条件可转化为先求点到平面的距离,即:作,垂足为,连接,作,垂足为,则由线面垂直的判定定理可得平面,再根据三角形面积相等:,可求出的长度,最后由三棱柱的高为此距离的两倍即可确定出高.
(3) 利用反三角函数分别求出,,使用面积公式求出每一面的面积,得到表面积.
(1)
证明:连接,则为与的交点,
∵侧面为菱形,∴.
∵平面,∴.
∵,平面 , 平面 ∴平面.
∵平面,∴.
(2)
解:作,垂足为,连接,作,垂足为,如图.
∵,,,平面,平面,
∴平面,∴.
∵,,平面,平面,
∴平面.
∵,∴为等边三角形.
∵,∴,
∵,∴,
由,且
,可得,
∵O为的中点,∴到平面的距离为,
∴三棱柱的高为.
(3)
解:易知,,
,,
,
∴,,,.
∴表面积为.
答案第1页,共2页
答案第1页,共2页
1.已知四面体的每个顶点都在球O(О为球心)的球面上,为等边三角形,,,且,则二面角的正切值为( )
A. B. C. D.
2.如图,棱长为2正方体,为底面的中心,点在侧面内运动且,则点到底面的距离与它到点的距离之和最小是( )
A. B. C. D.
3.如图,在正方体中,,,分别是,,的中点,则下列说法错误的是( )
A. B.平面
C.平面 D.与是异面直线
4.为提高学生数学学习的积极性,复旦附中联合浦东分校、青浦分校、复旦中学组织了复旦附中月度数学学科知识竞赛.本次比赛的年度总冠军奖杯由一个铜球O和一个底座组成,如图(1)所示,已知球的体积为,底座由边长为12的正三角形铜片ABC沿各边中点的连线垂直向上折叠成直二面角所得,如图(2)所示.则在图(1)所示的几何体中,下列结论中正确的是( )
A.CD与BE是异面直线
B.异面直线AB与CD所成角的大小为45°
C.由A、B、C三点确定的平面截球所得的截面面积为
D.球面上的点到底座底面DEF的最大距离为
5.如图,矩形中,,为边的中点.将沿直线翻折成(平面).若在线段上(点与,不重合),则在翻折过程中,给出下列判断:
①当为线段中点时,为定值;
②存在某个位置,使;
③当四棱锥体积最大时,点到平面的距离为;
④当二面角的大小为时,异面直线与所成角的余弦值为.
其中判断正确的个数为( )
A.1 B.2 C.3 D.4
6.如图所示,在正方体中,过对角线的一个平面交于E,交于F,给出下面几个命题:
①四边形一定是平行四边形;
②四边形有可能是正方形;
③平面有可能垂直于平面;
④设与DC的延长线交于M,与DA的延长线交于N,则M N B三点共线;
⑤四棱锥的体积为定值.
以上命题中真命题的个数为( )
A.2 B.3 C.4 D.5
二、多选题
7.如图,正方体棱长为1,P是上的一个动点,下列结论中正确的是( )
A.的最小值为
B.的最小值为
C.当P在直线上运动时,三棱锥的体积不变
D.以点B为球心,为半径的球面与面的交线长为
8.已知正方体的棱长为2,动点F在正方形内,则( )
A.若平面,则点F的位置唯一
B.若平面,则不可能垂直
C.若,则三棱锥的外接球表面积为
D.若点E为BC中点,则三棱锥的体积是三棱锥体积的一半
三、填空题
9.三棱锥体积为,且,则三棱锥外接球的表面积为____________.
10.已知正方体的棱长为2,M,N分别是的中点,点P是截面(包括边界)上的动点,,则与平面所成最大角的正切值为_______.
11.如图,在正方体,中,E,F,G分别为棱上的点(与正方体顶点不重合),过作平面,垂足为H.设正方体的棱长为1,给出以下四个结论:
①若E,F,G分别是的中点,则;
②若E,F,G分别是的中点,则用平行于平面的平面去截正方体,得到的截面图形一定是等边三角形;
③可能为直角三角形;
④.
其中所有正确结论的序号是________.
12.四棱锥A﹣BCDE的各顶点都在同一球面上,AB⊥底面BCDE,底面BCDE为梯形,∠BCD=60°,且AB=CB=BE=ED=2,则此球的表面积等于_________.
四、解答题
13.如图,在四棱锥中,是正三角形,四边形是菱形,,,点是的中点.
(1)求证:平面;
(2)若平面平面,求点到平面的距离.
14.已知正方体的棱长为a,E F分别为棱 的中点,P为体对角线所在直线上一动点.
(1)作出该正方体过点E F且和直线垂直的截面,并证明该截面和直线垂直;
(2)求出△EFP绕直线EF旋转而成的几何体体积的最小值;
(3)若动点M在直线EF上运动,动点N在平面上运动,求的最小值.
15.七面体玩具是一种常见的儿童玩具.在几何学中,七面体是指由七个面组成的多面体,常见的七面体有六角锥 五角柱 正三角锥柱 Szilassi多面体等.在拓扑学中,共有34种拓扑结构明显差异的凸七面体,它们可以看作是由一个长方体经过简单切割而得到的.在如图所示的七面体中,平面
(1)在该七面体中,探究以下两个结论是否正确.若正确,给出证明;若不正确,请说明理由:
①平面;
②平面;
(2)求该七面体的体积.
16.如图,三棱柱中,侧面为菱形,的中点为,且平面.
(1)证明:;
(2)若,,,求三棱柱的高;
(3)在(2)的条件下,求三棱柱的表面积.
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.A
【分析】若为中点,连接,利用线面垂直的判定、勾股定理及面面垂直判定可得面面,结合已知条件有△为等腰直角三角形,进而可确定四面体外接球球心的位置,若为中点,连接,易知即为二面角的平面角,即可求其正切值.
【详解】若为中点,连接,由为等边三角形,则,又,且,
∴面,又面,即,
由题设,,,而,
∴,即,又,面,
∴面,而面,则面面,
由上可得:,则,故△为等腰直角三角形,
∴综上,四面体的球心为△的中心,即靠近的三等分点,
若为中点,连接,易知:即为二面角的平面角,
由上、且,面,可得面,
又面,则,即,
∴,而,
∴.
故选:A.
【点睛】关键点点睛:根据线线垂直、勾股定理,结合线面、面面垂直的判定证面面且△为等腰直角三角形,即可确定四面体球心的位置,再由二面角的定义找到其平面角,最后由已知条件求其正切值即可.
2.A
【分析】取中点,连接,证明平面,求出P在FC上.将平面沿BC翻折到与平面ABCD共面,将B关于CF对称到,过作与E,则即为点到底面的距离与它到点的距离之和的最小值.
【详解】取中点,连接,
由,,可知,则,
∴由知,即.
∵平面ABCD,⊥平面ABCD,∴AC⊥,又AC⊥BD,BD∩=B,
∴平面,∵平面,∴,
∵,∴平面,
∵,∴平面,平面,
∵在侧面内,∴平面平面,即P在CF上;
∵平面⊥平面ABCD,且交线为BC,
∴P到平面ABCD的距离即为P到BC的距离,
将平面沿BC翻折到与平面ABCD共面,如图:
将B关于CF对称到,过作与E,则即为点到底面的距离与它到点的距离之和的最小值.
以B为原点,建立如图所示坐标系,则B(0,0),F(1,0),C(0,2),
直线CF方程为,即,
设,则,
∴.
故选:A﹒
3.D
【分析】根据所给条件和线面关系,逐项分析判断即可得解.
【详解】
对A,如图所示,连接,
因为点为中点,
所以,在正方体中易得,
所以,故A正确;
对B,如图所示,连接交于点,
连接,与交于点,连接,
在正方体中,易得,,
所以四边形为平行四边形,
则,又为中点,
点在上,则易知点为的中心点,
因为点为中点,所以,
又平面,平面,
所以平面,故B正确;
对C,如图所示,连接,
在正方体中,易知,
所以平面,又平面,
所以,
又为,中点,
则,又,所以,
所以平面,故C正确;
对D,如图所示,连接,
易知:又,
则,所以与共面,故D错误.
故选:D
4.C
【分析】取中点N,M,利用给定条件证明,推理判断A,B;求出外接圆半径,结合球面截面圆性质计算判断C,D作答.
【详解】取中点N,M,连接,如图,
因为正三角形,则,而平面平面,平面平面,平面,
于是得平面,同理平面,即,,
因此,四边形是平行四边形,有,则直线CD与BE在同一平面内,A不正确;
由选项A,同理可得,则异面直线AB与CD所成角等于直线DF与CD所成角,B不正确;
由选项A知,,同理可得,正外接圆半径,
由A、B、C三点确定的平面截球所得的截面圆是的外接圆,此截面面积为,C正确;
体积为的球半径,由得,由选项C知,球心到平面的距离,
由选项A,同理可得点A到平面的距离为,即平面与平面的距离为,
所以球面上的点到底座底面DEF的最大距离为,D不正确.
故选:C
【点睛】易错点睛:异面直线所成的角的取值范围是,当求出角的余弦值为负时,要取其相反数作为异面直线夹角余弦.
5.B
【分析】①利用余弦定理判断;②用线线垂直判断;③由垂线段判断;④由二面角与线线角公式判断.
【详解】在矩形 中, , 不妨令 2, 则:
(1)取DC的中点 , 连接 ,
易知 且为定值,
(定值)
所以MB的长为定值, 故①正确;
(2)假设存在某个位置, 使 , 连接 , 取DE的中点 , 连接 ,
显然 , 而 平面 ,
平面 ,
进而有 , 但 , 不可能相等,
所以不可能有 , 故②错误;
(3)由题意得, 是等腰直角三角形, 到 的距离是 ,
当平面 平面 时, 四棱雉 DE体积最大,
点 到平面 的距离为 , 故③正确;
(4)易知二面角 的平面角 , 当二面角 的大小为 时,
又 , 所以 ,
又易知异面直线 与 所成角为 ,
故④错误,
综上可知, 正确的有2个.
故选: B.
6.C
【分析】由面面平行的性质和四边形的判定定理可判断①;由正方形的性质可判断②;由面面垂直的判定定理可判断③;由两平面相交的性质可判断④;由等积法和棱锥的体积公式可判断⑤.
【详解】因为平面与平面平行,截面与它们交于,BF,可得,
同样可得,所以四边形是一个平行四边形,故①正确;
如果四边形是正方形,则,
因为,所以平面,
又平面,E与A重合,此时不是正方形,故②错误;
当两条棱上的交点是中点时,四边形为菱形,平面,
此时四边形垂直于平面,故③正确;
由与DC的延长线交于M,可得,且,
又因为平面,平面ABCD,
所以平面,平面ABCD,
又因为平面,平面ABCD,
所以平面平面,
同理平面平面,
所以BM,BN都是平面与平面ABCD的交线,
所以B,M,N三点共线,故④正确;
由于,平面,
则E,F到平面的距离相等,且为正方体的棱长,三角形的面积为定值,
所以四棱锥的体积为定值,故⑤正确.
故选:C.
【点睛】此题涉及的设问情况较多,有一定成立,有可能成立.对于一定成立的命题,需要利用定理加以证明,对于可能成立的问题举出例子即可说明其成立,利用反证法才能证明其不成立.故此类题在判断时,要学会选用适当的方法.
7.BCD
【分析】当时,BP最小,结合正三角形性质,求得B到直线的距离判断A,将平面翻折到平面上,求得PA+PC的最小值判断B,由题可得平面,进而可得三棱锥的体积不变,判断C,根据球的截面的性质可得以点B为球心,为半径的球面与面 的交线即为的内切圆,即可判断D.
【详解】对于A,当时,BP最小,由于
到直线的距离,故A错误;
对于B,将平面翻折到平面上,如图,
连接AC,与的交点即为点P,此时取最小值AC,
在三角形ADC中,,,故B正确;
对于C,由正方体的性质可得,平面,
平面,到平面的距离为定值,
又为定值,则为定值,即三棱锥的体积不变,故正确;
对于D,由于平面,设与平面交于点,
,设以为球心,为半径的球与面交线上任一点为,
,,
在以为圆心,为半径的圆上,
由于为正三角形,边长为 ,其内切圆半径为 ,
故此圆恰好为的内切圆,完全落在面内,
交线长为,故正确.
故选:BCD.
8.AD
【分析】求得点F的坐标判断选项A;求得同时满足两个条件的点F的坐标判断选项B;求得三棱锥的外接球表面积判断选项C;求得三棱锥的体积和三棱锥体积判断选项D.
【详解】如图,以D为原点分别以DA、DC、为x轴、y轴、z轴建立空间直角坐标系:
则,,,,,,,,
由于动点F在正方形内,可设,其中,,
选项A:若平面,则,.
由于,,,
则,解得:或(舍去),
此时,即点F的位置唯一,故选项A正确;
选项B:,,
设平面的一个法向量为.则,
令,得,,故,
而,若平面,则,
则,即,
所以,此时,
而,所以,
当时,,此时,则.故选项B不正确;
选项C:由于,则F为的中点,此时,
设三棱锥的的外接球的球心为,则,
即,解得:,
所以,则三棱锥的的外接球的半径为,
所以三棱锥的的外接球表面积为,
故选项C不正确;
选项D:点E为BC中点,由正方体可知平面,
则
则三棱锥的体积是三棱锥体积的一半. 故选项D正确.
故选:AD
9.
【分析】取BC中点D,连PD,连AD并延长至O1,使DO1=AD,连接BO1,CO1,PO1,
由条件证得O1是外接圆圆心及PO1⊥平面ABC,再判断外接球球心O位置经推理计算即可得解.
【详解】三棱锥中,取BC中点D,连PD,连AD并延长至O1,使DO1=AD,连接BO1,CO1,PO1,如图:
于是得四边形为平行四边形,而,是菱形,
在中,,由余弦定理有,即,
则,是正三角形,,于是得O1是外接圆圆心,
因,D为BC中点,则PD⊥BC,又AO1⊥BC,,平面,从而有平面,,
同理,而,从而得平面,由球的截面小圆性质知,三棱锥外接球球心O在直线上,
又,则,解得,
设球O的半径为R,则,,中,,即,解得,
则球O的表面积为,
所以三棱锥外接球的表面积为.
故答案为:
10.
【分析】先分析得到点P的轨迹是圆,然后将与平面所成最大角的正切值转化为求的最大正切值并计算即可.
【详解】取的中点O,连接,由正方体性质可知平面,则,即如下图(2),点P的轨迹是,半径为,又M到平面的距离为,因为,所E到的距离为,则为直线与平面的夹角,当O,T,P共线时,则此时最小,的值最大,,所以,
即.
故答案为:.
11.①④
【分析】①等体积法判断;②根据正方体的性质画出平行于平面的可能截面情况;③由正方体性质,通过定两点,移动另一点判断的内角变化趋势即可;④设,利用等体积法,结合正余弦定理、三角形面积公式、锥体体积公式化简即可判断.
【详解】①由,而,
所以,可得,正确;
②根据正方体的性质平行平面的平面有如下情况:
当截面在面与面之间时为六边形,在面左上或面右下时为等边三角形,错误;
③分别在上不为顶点任意点,当从到过程递减,即小于,同理知:也小于,不可能为直角三角形,错误;
④若,又,即,
所以,
则,即,
所以,即,正确;
故答案为:①④
【点睛】关键点点睛:①④应用等体积法计算或转化,②由正方体性质及平面的基本性质作出截面判断;③根据正方体的性质,动点分析三角形的内角变化趋势.
12.
【分析】由条件确定球心位置及球的半径,由此计算球的表面积.
【详解】若,又,则四边形BCDE为平行四边形,与条件矛盾,
∴ ,又CB=BE=ED=2,∠BCD=60°,
∴ CD=4,
∴ ,
∴是以CD为斜边的直角三角形,同理可得为CD为斜边的直角三角形,
∴ 四边形BCDE的外接圆圆心为CD的中点,记CD中点为,
设四棱锥A﹣BCDE的外接球的球心为O,则平面BCDE,
又AB⊥底面BCDE,
∴ ,设,设球的半径为R,过点O作,垂足为F,
∵ ,
∴ ,
∴ ,
∴ 球的半径,
∴ 球的表面积,
故答案为:.
【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.
13.(1)证明见解析;(2).
【分析】(1)连接交于,利用中位线易得∥,进而利用线面平行的判定定理即可证明;
(2)取中点,利用面面垂直得平面,从而可求得,利用等体积法即可求解点到平面的距离.
【详解】(1)在四棱锥S ABCD中,连接交于,则为中点,连接,又为中点,∴,又平面,平面,∴平面.
(2)∵四边形是菱形,且,∴为正三角形,取中点的,连接,,则,∵平面平面,平面平面,∴平面,
∵均是正三角形,AB=2,易得, ,
∴.
易得,由,∴,
取的中点,连接,因为,∴,
∴,可得,
设点到平面的距离为,∴,
解得,即点到平面的距离为.
14.(1)见解析;
(2);
(3)a.
【分析】(1)取DD1中点为G,连接FG、EG,则⊥平面EFG.
(2)由(1)知⊥平面EFG,设,
由图可知此时△EFP的高为PH,且此时△EFP的高最短,△EFP绕EF旋转成的几何体体积最小,该几何体为两个相同的圆锥的组合体,圆锥底面半径为PH,高为EH.
(3)P在上,在平面投影为在平面上的投影为,则要使|PM|+|PN|最小,M点为EF中点,N点上,且有PN⊥.
将平面沿翻折到平面内,作M点关于的对称点,则过作N⊥与N,N即为|PM|+|PN|的最小值.
【详解】(1)如图,取DD1中点为G,连接FG、EG,则⊥平面EFG.
证明如下:设EF和交点为H,连接GH,
∴GH⊥.
连接,则⊥,又由⊥平面知,
故⊥平面,∴⊥,
∵E F分别为棱 的中点,∴,∴EF⊥,
又GHEF=H,GH和EF平面EFG,∴⊥平面EFG.
(2)由(1)知⊥平面EFG,设,
由图可知此时△EFP的高为PH,且此时△EFP的高最短,△EFP绕EF旋转成的几何体体积最小,该几何体为两个相同的圆锥的组合体,圆锥底面半径为PH,高为EH.
|EH|=|EF|=,
在△BDD1中,,
在△中,,
,
,
形成的几何体的体积为.
(3)P在上,在平面投影为在平面上的投影为,
则要使|PM|+|PN|最小,M点为EF中点,N点上,且有PN⊥.
将平面沿翻折到平面内,如图所示,作M点关于的对称点,则过作N⊥与N,N即为|PM|+|PN|的最小值.
∵,
,
,
,
∥,
∵∥,
∴四边形为平行四边形,
.
即|PM|+|PN|最小值为a.
15.(1)结论①正确;证明见解析;结论②错误;答案见解析;(2).
【分析】(1)①由平行四边形得线线平行,再得线面平行;
②假设平面,平面,得平面,得,
但,所以,与矛盾,故②错误.
(2)将七面体进行分解,
七面体的体积等于,转化为容易求体积的几何体来计算;
也可补形为长方体,通过来求解;
以及利用空间直角坐标系也行.
【详解】(1)结论①正确,结论②错误,理由如下:
对于结论①,因为且,连接,
所以四边形是平行四边形,
所以,因为平面,平面,
平面结论①正确
对于结论②,若,则,
因为平面,,所以平面,
所以,又因为,所以平面,
所以,而在梯形中,,
,所以,与矛盾
所以结论②错误.
(2)方法一:连接,交于点,连接,
则在平面中,与EG相交,
设交点为,则由可得,
又,
该七面体的体积等于
方法二:将该七面体补成如图所示的长方体;
方法三:建立空间直角坐标系,利用空间向量求点到平面的距离
后求三棱锥的体积.(参照给分
【点睛】充分利用题目信息,特别是几何体的几何特征,并会假设结论成立,推导,若得出矛盾,则假设错误,否则假设成立.复杂的不规则的几何体体积求解,需要转化为常见几何体的体积来解.
16.(1)证明见解析
(2)
(3)
【分析】(1)要证,即证平面,由菱形的对角线垂直和线面垂直的性质即可得证.
(2) 要求三菱柱的高,根据题中已知条件可转化为先求点到平面的距离,即:作,垂足为,连接,作,垂足为,则由线面垂直的判定定理可得平面,再根据三角形面积相等:,可求出的长度,最后由三棱柱的高为此距离的两倍即可确定出高.
(3) 利用反三角函数分别求出,,使用面积公式求出每一面的面积,得到表面积.
(1)
证明:连接,则为与的交点,
∵侧面为菱形,∴.
∵平面,∴.
∵,平面 , 平面 ∴平面.
∵平面,∴.
(2)
解:作,垂足为,连接,作,垂足为,如图.
∵,,,平面,平面,
∴平面,∴.
∵,,平面,平面,
∴平面.
∵,∴为等边三角形.
∵,∴,
∵,∴,
由,且
,可得,
∵O为的中点,∴到平面的距离为,
∴三棱柱的高为.
(3)
解:易知,,
,,
,
∴,,,.
∴表面积为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
