2.露在外面的面同步练习五年级数学下册(北师大版)含答案
文档属性
| 名称 | 2.露在外面的面同步练习五年级数学下册(北师大版)含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 138.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 00:00:00 | ||
图片预览


文档简介
2.露在外面的面 同步练习
五年级数学下册(北师大版)含答案
一、填空题
1.如图,4个棱长都是3分米的正方体堆放在墙角处,露在外面的面的面积总和是( )平方分米。
(第1题) (第2题)
2.如图,4个棱长为5分米的正方体纸箱堆放在墙角,有( )个面露在外面,露在外面的面积是( )平方分米。
3.把一个长是12厘米、宽是8厘米、高是6厘米的长方体木块表面涂成红色,然后切成棱长是2厘米的小正方体,可以切成( )块小正方体,只有3面涂色的小正方体有( )块,只有2面涂色的小正方体有( )块,只有1面涂色的小正方体有( )块,没有涂色的小正方体有( )块。
4.将若干个小正方体按如图方式摆放在桌面上,
如果摆6个,则一共有( )个面露在外面;
如果摆x个,则一共有( )个面露在外面;
当摆( )个时,有29个面露在外面。
5.把27个相同的小正方体拼成一个大正方体,把它的表面全部涂色。
(1)两面涂色的有( )块。
(2)三面涂色的有( )块。
(3)没有涂色的有( )块。
6.一个长方体等分成两份,变成了两个小正方体,表面积比原来增加了50平方厘米,原来长方体的表面积是( )平方厘米。
7.如图,淘气和笑笑各搬了7个棱长为10厘米的正方体纸箱放在墙角。
(1)淘气摆放的纸箱有( )个面露在外边,露在外面的面积是( )平方厘米。
(2)笑笑摆放的纸箱有( )个面露在外边,露在外面的面积是( )平方厘米。
二、选择题
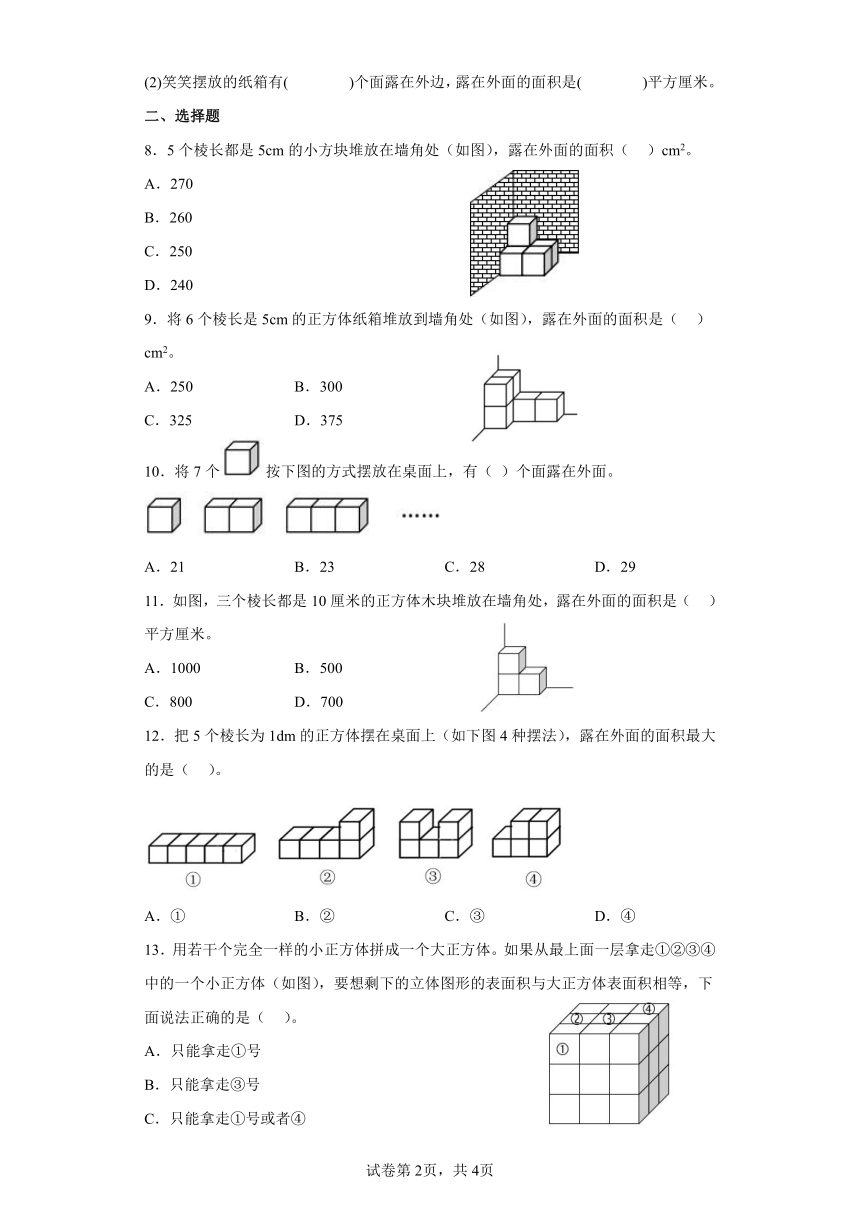
8.5个棱长都是5cm的小方块堆放在墙角处(如图),露在外面的面积( )cm2。
A.270
B.260
C.250
D.240
9.将6个棱长是5cm的正方体纸箱堆放到墙角处(如图),露在外面的面积是( )cm2。
A.250 B.300
C.325 D.375
10.将7个按下图的方式摆放在桌面上,有( )个面露在外面。
A.21 B.23 C.28 D.29
11.如图,三个棱长都是10厘米的正方体木块堆放在墙角处,露在外面的面积是( )平方厘米。
A.1000 B.500
C.800 D.700
12.把5个棱长为1dm的正方体摆在桌面上(如下图4种摆法),露在外面的面积最大的是( )。
A.① B.② C.③ D.④
13.用若干个完全一样的小正方体拼成一个大正方体。如果从最上面一层拿走①②③④中的一个小正方体(如图),要想剩下的立体图形的表面积与大正方体表面积相等,下面说法正确的是( )。
A.只能拿走①号
B.只能拿走③号
C.只能拿走①号或者④
D.只能拿走②号
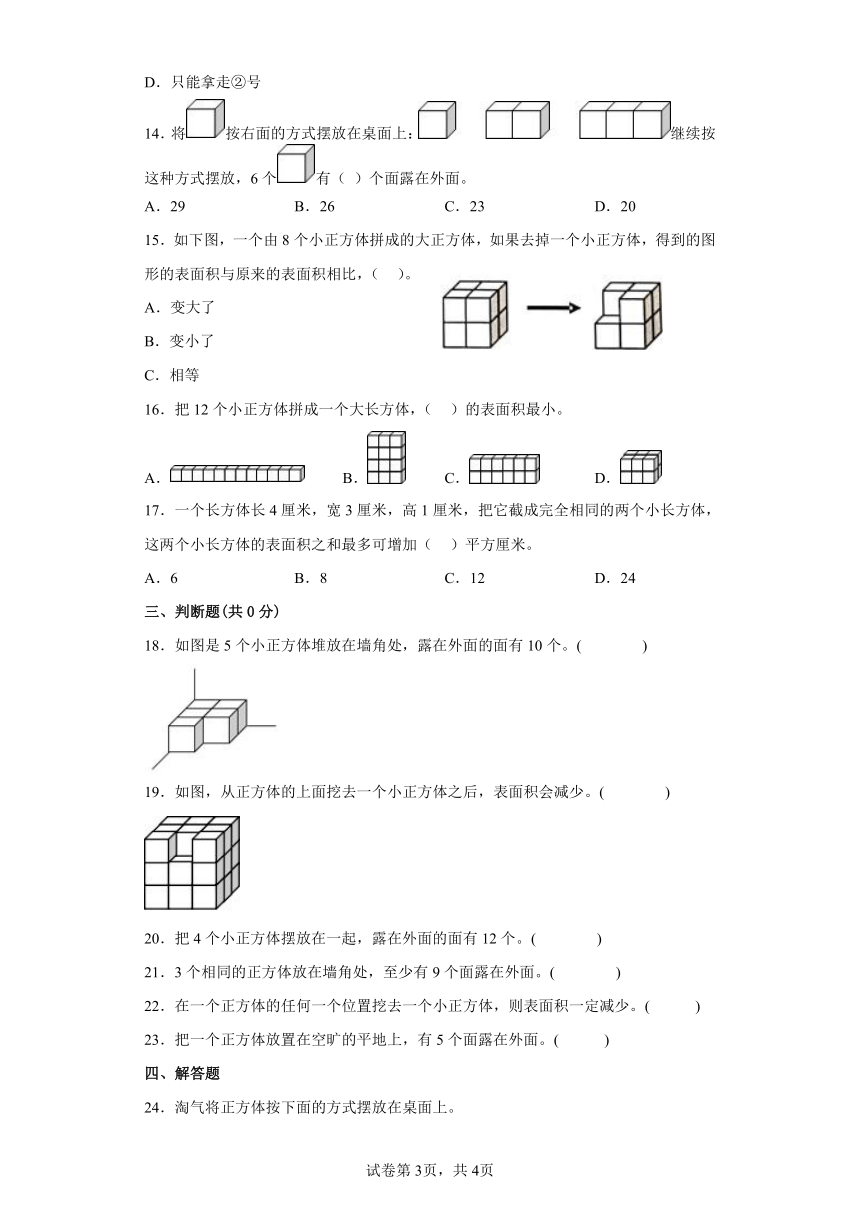
14.将按右面的方式摆放在桌面上:继续按这种方式摆放,6个有( )个面露在外面。
A.29 B.26 C.23 D.20
15.如下图,一个由8个小正方体拼成的大正方体,如果去掉一个小正方体,得到的图形的表面积与原来的表面积相比,( )。
A.变大了
B.变小了
C.相等
16.把12个小正方体拼成一个大长方体,( )的表面积最小。
A. B. C. D.
17.一个长方体长4厘米,宽3厘米,高1厘米,把它截成完全相同的两个小长方体,这两个小长方体的表面积之和最多可增加( )平方厘米。
A.6 B.8 C.12 D.24
三、判断题(共0分)
18.如图是5个小正方体堆放在墙角处,露在外面的面有10个。( )
19.如图,从正方体的上面挖去一个小正方体之后,表面积会减少。( )
20.把4个小正方体摆放在一起,露在外面的面有12个。( )
21.3个相同的正方体放在墙角处,至少有9个面露在外面。( )
22.在一个正方体的任何一个位置挖去一个小正方体,则表面积一定减少。( )
23.把一个正方体放置在空旷的平地上,有5个面露在外面。( )
四、解答题
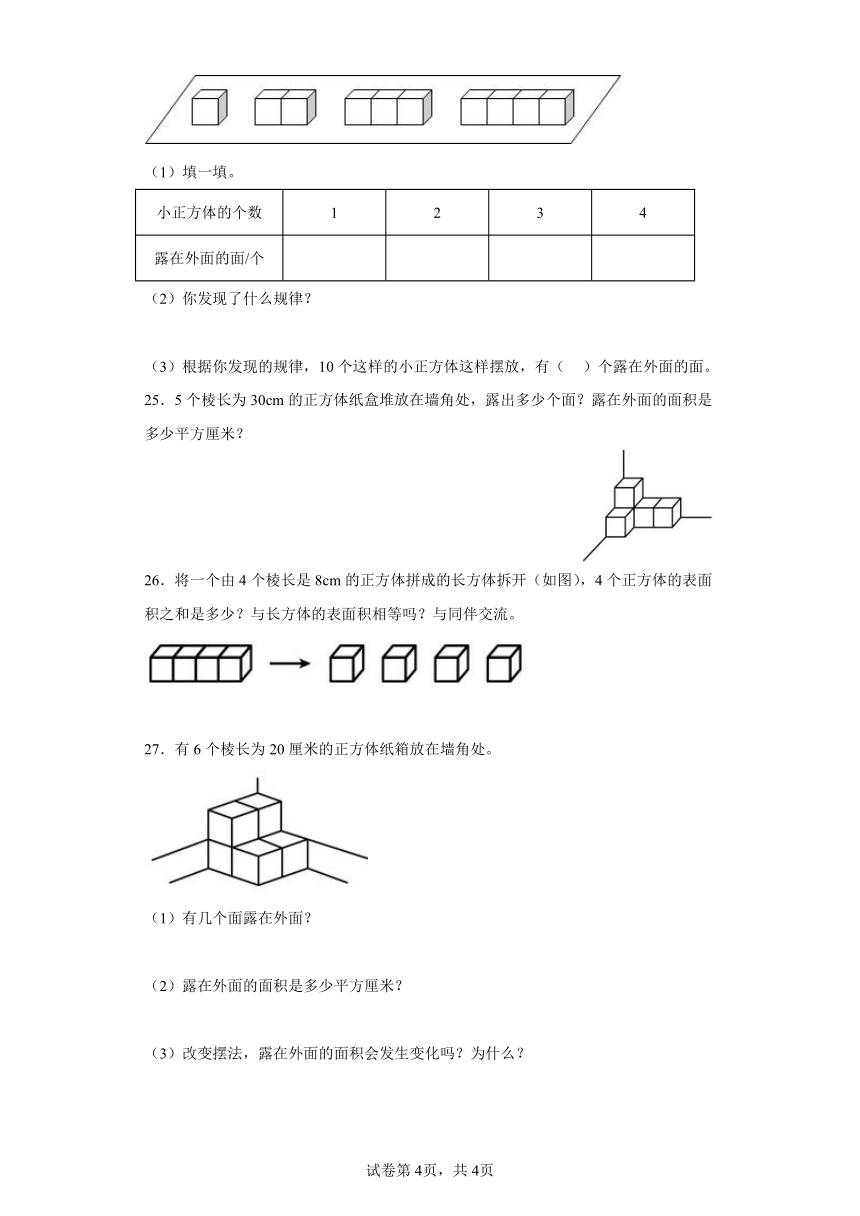
24.淘气将正方体按下面的方式摆放在桌面上。
(1)填一填。
小正方体的个数 1 2 3 4
露在外面的面/个
(2)你发现了什么规律?
(3)根据你发现的规律,10个这样的小正方体这样摆放,有( )个露在外面的面。
25.5个棱长为30cm的正方体纸盒堆放在墙角处,露出多少个面?露在外面的面积是多少平方厘米?
26.将一个由4个棱长是8cm的正方体拼成的长方体拆开(如图),4个正方体的表面积之和是多少?与长方体的表面积相等吗?与同伴交流。
27.有6个棱长为20厘米的正方体纸箱放在墙角处。
(1)有几个面露在外面?
(2)露在外面的面积是多少平方厘米?
(3)改变摆法,露在外面的面积会发生变化吗?为什么?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.81
【分析】通过对该组合体的观察,该组合体从前面看,有3个小正方形,从上面看,有3个小正方形,从右面看,有3个小正方形,把这三个方位能看见的小正方形数量加起来,通过正方形面积公式:S=a2,代入数据求出1个小正方形的面积,再乘总共露在外面的小正方形数量即可。
【详解】露在外面的小正方形数量为:
3+3+3
=6+3
=9(个)
1个小正方形面积为:
3×3=9(平方分米)
露在外面的面的面积总和是:9×9=81(平方分米)
2. 8 200
【分析】根据从不同方向看到的图形的形状可知,从正面看到的是2个小正方形,从上面看到的是4个小正方形,从右面看到的是2个小正方形,求一共看到的是几个即可;然后用总个数乘1个小正方形的面积即可。
【详解】2+4+2=8(个)
5×5×8
=25×8
=200(平方分米)
3. 72 8 28 28 8
【分析】根据长方体切割正方体的特点可得:12÷2=6块,8÷2=4块,6÷2=3块,将各条棱上所得的正方体块数相乘可以求得小正方体的总块数;3面涂色的木块在顶点位置,2面涂色的木块在棱上非顶点的位置,1面涂色的木块在每个面上非棱上的位置,没有涂色的木块用所有小木块的数量减去涂色木块的数量求解。
【详解】12÷2=6(块)
8÷2=4(块)
6÷2=3(块)
可以切成:6×4×3=72(块);
3面涂色的木块在顶点位置,所以只有8块;
2面涂色的木块在棱上非顶点的位置
(6-2)×4+(4-2)×4+(3-2)×4
=4×4+2×4+1×4
=16+8+4
=28(块)
1面涂色的木块在每个面上非棱上的位置
(6-2)×(4-2)×2+(6-2)×(3-2)×2+(4-2)×(3-2)×2
=4×2×2+4×1×2+2×1×2
=16+8+4
=28(块)
没有涂色的数量为:
72-8-28-28=8(块)
4. 20 3x+2 9
【分析】摆1个小正方体,有5个面露面外面,摆2个小正方体,有8个面露在外面,摆3个小正方体,有11个面露在外面,可得露在外面的面的个数=序数×3+2,据此作答。
【详解】根据分析可知,露在外面的面的个数=序数×3+2,所以如果摆6个,则一共有:
6×3+2
=18+2
=20(个)
20个面露在外面;
如果摆x个,则一共有(3x+2)个面露在外面;
3x+2=29
3x=27
x=9
当摆9个时,有29个面露在外面。
5.(1)12
(2)8
(3)1
【分析】(1)小正方体组成的大正方体的每个顶点处的小正方体三面涂色,位于每条棱非两端的都是两面涂色,一个正方体有12条棱,每条棱上1块,有12块两面涂色;
(2)大正方体有8个顶点,三面涂色是8块;
(3)处于每个面非边缘的小正方体一面涂色,即小正方体位于每个面中间的1面涂色,大正方体有6个面,一面涂色的就是6块;用27减去三面涂色的块数,减去两面涂色的块数减去一面涂色的块数,即可求出没有涂色的块数。
(1)
两面涂色的有12块
(2)
三面涂色的有8块
(3)
一面涂色的有6块
没涂色的:
27-12-8-6
=15-8-6
=7-6
=1(块)
没有涂色的有1块。
6.250
【分析】根据长方体截成两个相等的正方体,则长方体的表面积就等于小正方体的10个面的面积之和,根据切割的特点,增加了2个面,增加的面积已知,从而可求出一个正方形的面积,再乘10就是原来的长方体的表面积。
【详解】一个小正方形的面积:
50÷2=25(平方厘米)
原来长方体的表面积:
25×10=250(平方厘米)
7.(1) 13 1300
(2) 12 1200
【分析】(1)根据图示可知,淘气摆的纸箱因为放在墙角处,所以有三面靠墙的在内部,所以露在外部的有:正面5个正方形,右面5个正方形,上面3个正方形,一共有5+5+3=13(个),每个小正方形面的面积是10×10=100(平方厘米),据此再乘13就是露在外部的总面积。
(2)根据图示可知,笑笑摆的纸箱因为放在墙角处,所以有三面靠墙的在内部,所以露在外部的有:正面4个正方形,右面4个正方形,上面4个正方形,一共有4+4+4=12(个),每个小正方形面的面积是10×10=100(平方厘米),据此再乘12就是露在外部的总面积。
(1)
5+5+3=13(个)
10×10×13=1300(平方厘米)
(2)
4+4+4=12(个)
10×10×12=1200(平方厘米)
8.C
【分析】根据题意,露在外面的面一共有10个,一个面的面积为(5×5)cm2,据此用乘法求出10个面的面积即可。
【详解】根据题意得
5×5×10
=25×10
=250(cm2)
露在外面的面积250cm2。
故答案为:C
9.B
【分析】观察图形可知,从上面看到的是4个正方形面,从前面看到是4个正方形面,从右面看到的是4个正方形面,把从上面、右面、前面看到的面相加,可算出总共露出来多少个小正方形,再根据正方形面积公式:S=a×a,求出1个正方形的面积,最后乘正方形的个数即可。
【详解】露出来的正方形总个数为:
4+4+4
=8+4
=12(个)
1个正方形面积为:
5×5=25(cm2)
露在外面的面积是:
25×12=300(cm2)
故答案为:B
10.B
【分析】观察正方体的摆放,第一个图有1×3+2=5(个)面露在外面,第二个图有2×3+2=8(个)面露在外面,第三个图有3×3+2=11(个)面露在外面,那么每增加1个小正方体就增加3个面露在外面。由此解题即可。
【详解】3×7+2
=21+2
=23(个)
所以,将7个按图中的方式摆放在桌面上,有23个面露在外面。
故答案为:B
11.D
【分析】观察图形可知,从正面看,有3个面露在外面;从上面看,有2个面露在外面;从右侧看,有2个面露在外面;一共有3+2+2=7个面露在外面;再根据正方形面积公式:面积=边长×边长,代入数据,求出一个正方形面积,再乘露出外面面的个数,即可解答。
【详解】3+2+2
=5+2
=7(个)
10×10×7
=100×7
=700(平方厘米)
故答案为:D
12.C
【分析】先数清各选项露在外面的面的个数,再根据正方形面积公式:边长×边长,代入数据,求出一个面的面积,再乘露在外面的面的个数,求出露在外面的面的面积,进行比较,即可解答。
【详解】A. 一共有17个面露在外面;面积:1×1×17=17(dm2);
B. 一共有18个面露在外面;面积:1×1×18=18(dm2);
C.一共有19个面露在外面;面积:1×1×19=19(dm2);
D.一共有17个面露在外面,面积:1×1×17=17(dm2)。
故答案为:C
13.C
【分析】看图可知,拿走①或④,减少了三个面,同时又增加了三个面,则图形的表面积没有变;拿走②,减少了两个面,同时又增加了四个面,则图形的表面积增大;拿走③,减少了一个面,同时又增加了五个面,则图形的表面积增大;据此判断即可。
【详解】根据分析可知:若干个完全一样的小正方体拼成一个大正方体。如果从最上面一层拿走①②③④中的一个小正方体(如图),要想剩下的立体图形的表面积与大正方体表面积相等,只能拿走①号或者④。
故答案为:C
14.D
【分析】1个小正体有5个面露在外面,再增加一个正方体,2个小正方体有8个面露在外面;3个小正方体有11个面露在外面.每增加1个正方体漏在外面的面就增加3个即:n个正方体有5+(n-1)×3;由此求解。解答此题应根据题意,进行推导,得出规律:即1个小正方体露出5个面,每增加1个小正方体增加3个面;进行解答即可。
【详解】根据分析可知,6个正方体有:
5+(6-1)×3
=5+5×3
=5+15
=20(个)
故答案为:D
15.C
【分析】观察图形可知,在大正方体的顶点位置去掉一个小正方形,虽然减少了3个小正方形的面积,但产生的切面上又增加了3个小正方形的面积,所以得到图形的表面积与原来正方体的表面积相等。
【详解】通过分析,一个由8个小正方体拼成的大正方体,如果去掉一个小正方体,得到的图形的表面积与原来的表面积相等。
故答案为:C
16.D
【分析】根据正方体拼组长方体的方法,可以将12分解质因数,12=2×2×3,所以12个小正方体拼成的大长方体有:12×1×1、 4×3×1、 2×6×1、2×2×3共四种情况,其中2×2×3减少的面最多,所以拼成的长方体的表面积最小,也可以利用长方体表面积计算公式计算出组合图形的表面积进行比较得出答案。
【详解】假设一个小正方体的棱长是1分米。
选项A的表面积:(1×12+1×12+1×1)×2
=(12+12+1)×2
=25×2
=50(平方分米)
选项B的表面积:(3×1+1×4+3×4)×2
=(3+4+12)×2
=19×2
=38(平方分米)
选项C的表面积:(2×1+1×6+2×6)×2
=(2+6+12)×2
=20×2
=40(平方分米)
选项D的表面积:(2×2+2×3+2×3)×2
=(4+6+6)×2
=16×2
=32(平方分米)
因为32<38<40<50,所以选项B的表面积最小。
故答案为:D
17.D
【分析】把这个长方体截成完全相同的两个小长方体,可以从上面横切,增加的面积是4×1×2=8(平方厘米);可以从上面竖切,增加的面积是3×1×2=6(平方厘米);也可以沿水平方向切,增加的面积是4×3×2=24(平方厘米)。据此解答。
【详解】通过分析可知,把这个长方体沿水平分向切成两个小长方体,表面积之和增加最多,最多增加4×3×2=24(平方厘米)。
故答案为:D
18.√
【分析】分别数出从各个方向看到的这些正方形的面数,相加即可。
【详解】从正面看,可以看到2个正方形;
从右面看,可以看到3个正方形;
从上面看,可以看到5个正方形。
露在外面的面有:
2+3+5
=5+5
=10(个)
故答案为:√
19.×
【分析】大正方体挖去一个小正方体,仔细观察,凹下去图形是4个面的面积,而原来缺失的是2个面的面积,所以大正方体的表面积和以前相比,多了2个面的面积,据此解答。
【详解】根据分析,这个组合体的表面积与之前相比,表面积增加了。所以原题的说法是错误的。
故答案为:×
20.×
【分析】把4个小正方体摆放在一起,摆放的方法有多种。如果4个摆成一排,从上面看有4个面,从前、后看有8个面,左、右各看到1个面,则露在外面的面是4+8+2=14(个);如果再用不同的摆法,露在外面的面的数量也是不同的。
【详解】通过分析可知,不同的摆法,露在外面的面的数量也不同。原题说法错误。
故答案为:×
21.×
【分析】将3个相同的正方体放在墙角处,如图有三种不同的方法:
,数出露在外面的面一共有几个,再进一步解答即可。
【详解】由分析可知:可以摆如下图所示的三种情况。
以上三种直观图露在外面的面都是7个,原说法错误。
故答案为:×
22.×
【分析】在一个正方体的顶点位置挖去一个小正方体,表面积不变;在一个正方体棱的位置挖去一个小正方体,表面积增加;在一个正方体面上挖去一个小正方体,则表面积增加。据此解答。
【详解】在一个正方体的任何一个位置挖去一个小正方体,则表面积会增加或不变。
故答案为:×
23.√
【分析】正方体有6个面,放在空旷的平地上说明只有下面的一个面被挡住了,所以有5个面露在外面。据此判断。
【详解】把一个正方体放置在空旷的平地上,有5个面露在外面。此说法正确,故答案为:正确。
24.(1)5;8;11;14;(2)见详解;(3)32
【分析】(1)观察图形,小正方体的个数为1时,露在外面的面有5个面,小正方体的个数为2时,露在外面的面有(5+3)个面,小正方体的个数为3时,露在外面的面有(5+3×2)个面,小正方体的个数为4时,露在外面的面有(5+3×3)个面,据此完成填空。
(2)通过前面计算出来的数据,我们可以看出随着小正方体的个数的增多,露在外面的面的个数也在增加,具体的变化规律是当前图形露在外面的面的个数比前一个露在外面的面的个数要多3个。
(3)依次类推,小正方体的个数为n时,露在外面的面有个面,当n=10时,把数据代入,即可求出有多少个露在外面的面。
【详解】(1)5+3=8(个)
5+3×2
=5+6
=11(个)
5+3×3
=5+9
=14(个)
填表如下:
小正方体的个数 1 2 3 4
露在外面的面/个 5 8 11 14
(2)答:我发现当前图形露在外面的面的个数比前一个露在外面的面的个数要多3个。
(3)小正方体的个数为n时,露在外面的面有个面,
当n=10时,
=
=
=5+27
=32(个)
25.11个;9900平方厘米
【分析】从上面看,能看到4个面,从正面看,能看到4个面,从右面看,能看到3个面,这样共能够看到4+4+3=11个面,正方体的棱长已知,棱长×棱长求出1个面的面积,再乘11就可以求出露在外面的面积。
【详解】4+4+3
=8+3
=11(个)
30×30×11
=900×11
=9900(平方厘米)
答:露出11个面,露在外面的面积是9900平方厘米。
26.1536cm2;不相等
【分析】4个正方体的表面积之和=棱长×棱长×6×4,将一个由4个棱长是8cm的正方体拼成的长方体拆开,表面积增加了6个面的面积。
【详解】8×8×6×4
=64×6×4
=1536(cm2)
将一个由4个棱长是8cm的正方体拼成的长方体拆开,表面积增加了6个面的面积,与原来长方体的表面积不相等。
答:4个正方体的表面积之和是1536cm2,与长方体的表面积不相等。
27.(1)11个
(2)4400平方厘米
(3)可能不变,也可能会发生变化;因为露在外面的面数不确定
【分析】(1)露在外部的有:正面3个正方形,右面4个正方形,上面4个正方形,一共有3+4+4=11(个);
(2)每个小正方形面的面积是20×20=400(平方厘米),据此再乘11就是露在外部的总面积;
(3)改变摆法,露在外面的面积可能不变,也可能会发生变化,因为露在外面的面数不确定。
【详解】(1)正面3个正方形,右面4个正方形,上面4个正方形,
3+4+4
=7+4
=11(个)
答:有11个面露在外面。
(2)20×20×11
=400×11
=4400(平方厘米)
答:露在外面的面积是4400平方厘米。
(3)改变摆法,露在外面的面积可能不变,也可能会发生变化,因为露在外面的面数不确定。
答案第1页,共2页
答案第1页,共2页
五年级数学下册(北师大版)含答案
一、填空题
1.如图,4个棱长都是3分米的正方体堆放在墙角处,露在外面的面的面积总和是( )平方分米。
(第1题) (第2题)
2.如图,4个棱长为5分米的正方体纸箱堆放在墙角,有( )个面露在外面,露在外面的面积是( )平方分米。
3.把一个长是12厘米、宽是8厘米、高是6厘米的长方体木块表面涂成红色,然后切成棱长是2厘米的小正方体,可以切成( )块小正方体,只有3面涂色的小正方体有( )块,只有2面涂色的小正方体有( )块,只有1面涂色的小正方体有( )块,没有涂色的小正方体有( )块。
4.将若干个小正方体按如图方式摆放在桌面上,
如果摆6个,则一共有( )个面露在外面;
如果摆x个,则一共有( )个面露在外面;
当摆( )个时,有29个面露在外面。
5.把27个相同的小正方体拼成一个大正方体,把它的表面全部涂色。
(1)两面涂色的有( )块。
(2)三面涂色的有( )块。
(3)没有涂色的有( )块。
6.一个长方体等分成两份,变成了两个小正方体,表面积比原来增加了50平方厘米,原来长方体的表面积是( )平方厘米。
7.如图,淘气和笑笑各搬了7个棱长为10厘米的正方体纸箱放在墙角。
(1)淘气摆放的纸箱有( )个面露在外边,露在外面的面积是( )平方厘米。
(2)笑笑摆放的纸箱有( )个面露在外边,露在外面的面积是( )平方厘米。
二、选择题
8.5个棱长都是5cm的小方块堆放在墙角处(如图),露在外面的面积( )cm2。
A.270
B.260
C.250
D.240
9.将6个棱长是5cm的正方体纸箱堆放到墙角处(如图),露在外面的面积是( )cm2。
A.250 B.300
C.325 D.375
10.将7个按下图的方式摆放在桌面上,有( )个面露在外面。
A.21 B.23 C.28 D.29
11.如图,三个棱长都是10厘米的正方体木块堆放在墙角处,露在外面的面积是( )平方厘米。
A.1000 B.500
C.800 D.700
12.把5个棱长为1dm的正方体摆在桌面上(如下图4种摆法),露在外面的面积最大的是( )。
A.① B.② C.③ D.④
13.用若干个完全一样的小正方体拼成一个大正方体。如果从最上面一层拿走①②③④中的一个小正方体(如图),要想剩下的立体图形的表面积与大正方体表面积相等,下面说法正确的是( )。
A.只能拿走①号
B.只能拿走③号
C.只能拿走①号或者④
D.只能拿走②号
14.将按右面的方式摆放在桌面上:继续按这种方式摆放,6个有( )个面露在外面。
A.29 B.26 C.23 D.20
15.如下图,一个由8个小正方体拼成的大正方体,如果去掉一个小正方体,得到的图形的表面积与原来的表面积相比,( )。
A.变大了
B.变小了
C.相等
16.把12个小正方体拼成一个大长方体,( )的表面积最小。
A. B. C. D.
17.一个长方体长4厘米,宽3厘米,高1厘米,把它截成完全相同的两个小长方体,这两个小长方体的表面积之和最多可增加( )平方厘米。
A.6 B.8 C.12 D.24
三、判断题(共0分)
18.如图是5个小正方体堆放在墙角处,露在外面的面有10个。( )
19.如图,从正方体的上面挖去一个小正方体之后,表面积会减少。( )
20.把4个小正方体摆放在一起,露在外面的面有12个。( )
21.3个相同的正方体放在墙角处,至少有9个面露在外面。( )
22.在一个正方体的任何一个位置挖去一个小正方体,则表面积一定减少。( )
23.把一个正方体放置在空旷的平地上,有5个面露在外面。( )
四、解答题
24.淘气将正方体按下面的方式摆放在桌面上。
(1)填一填。
小正方体的个数 1 2 3 4
露在外面的面/个
(2)你发现了什么规律?
(3)根据你发现的规律,10个这样的小正方体这样摆放,有( )个露在外面的面。
25.5个棱长为30cm的正方体纸盒堆放在墙角处,露出多少个面?露在外面的面积是多少平方厘米?
26.将一个由4个棱长是8cm的正方体拼成的长方体拆开(如图),4个正方体的表面积之和是多少?与长方体的表面积相等吗?与同伴交流。
27.有6个棱长为20厘米的正方体纸箱放在墙角处。
(1)有几个面露在外面?
(2)露在外面的面积是多少平方厘米?
(3)改变摆法,露在外面的面积会发生变化吗?为什么?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.81
【分析】通过对该组合体的观察,该组合体从前面看,有3个小正方形,从上面看,有3个小正方形,从右面看,有3个小正方形,把这三个方位能看见的小正方形数量加起来,通过正方形面积公式:S=a2,代入数据求出1个小正方形的面积,再乘总共露在外面的小正方形数量即可。
【详解】露在外面的小正方形数量为:
3+3+3
=6+3
=9(个)
1个小正方形面积为:
3×3=9(平方分米)
露在外面的面的面积总和是:9×9=81(平方分米)
2. 8 200
【分析】根据从不同方向看到的图形的形状可知,从正面看到的是2个小正方形,从上面看到的是4个小正方形,从右面看到的是2个小正方形,求一共看到的是几个即可;然后用总个数乘1个小正方形的面积即可。
【详解】2+4+2=8(个)
5×5×8
=25×8
=200(平方分米)
3. 72 8 28 28 8
【分析】根据长方体切割正方体的特点可得:12÷2=6块,8÷2=4块,6÷2=3块,将各条棱上所得的正方体块数相乘可以求得小正方体的总块数;3面涂色的木块在顶点位置,2面涂色的木块在棱上非顶点的位置,1面涂色的木块在每个面上非棱上的位置,没有涂色的木块用所有小木块的数量减去涂色木块的数量求解。
【详解】12÷2=6(块)
8÷2=4(块)
6÷2=3(块)
可以切成:6×4×3=72(块);
3面涂色的木块在顶点位置,所以只有8块;
2面涂色的木块在棱上非顶点的位置
(6-2)×4+(4-2)×4+(3-2)×4
=4×4+2×4+1×4
=16+8+4
=28(块)
1面涂色的木块在每个面上非棱上的位置
(6-2)×(4-2)×2+(6-2)×(3-2)×2+(4-2)×(3-2)×2
=4×2×2+4×1×2+2×1×2
=16+8+4
=28(块)
没有涂色的数量为:
72-8-28-28=8(块)
4. 20 3x+2 9
【分析】摆1个小正方体,有5个面露面外面,摆2个小正方体,有8个面露在外面,摆3个小正方体,有11个面露在外面,可得露在外面的面的个数=序数×3+2,据此作答。
【详解】根据分析可知,露在外面的面的个数=序数×3+2,所以如果摆6个,则一共有:
6×3+2
=18+2
=20(个)
20个面露在外面;
如果摆x个,则一共有(3x+2)个面露在外面;
3x+2=29
3x=27
x=9
当摆9个时,有29个面露在外面。
5.(1)12
(2)8
(3)1
【分析】(1)小正方体组成的大正方体的每个顶点处的小正方体三面涂色,位于每条棱非两端的都是两面涂色,一个正方体有12条棱,每条棱上1块,有12块两面涂色;
(2)大正方体有8个顶点,三面涂色是8块;
(3)处于每个面非边缘的小正方体一面涂色,即小正方体位于每个面中间的1面涂色,大正方体有6个面,一面涂色的就是6块;用27减去三面涂色的块数,减去两面涂色的块数减去一面涂色的块数,即可求出没有涂色的块数。
(1)
两面涂色的有12块
(2)
三面涂色的有8块
(3)
一面涂色的有6块
没涂色的:
27-12-8-6
=15-8-6
=7-6
=1(块)
没有涂色的有1块。
6.250
【分析】根据长方体截成两个相等的正方体,则长方体的表面积就等于小正方体的10个面的面积之和,根据切割的特点,增加了2个面,增加的面积已知,从而可求出一个正方形的面积,再乘10就是原来的长方体的表面积。
【详解】一个小正方形的面积:
50÷2=25(平方厘米)
原来长方体的表面积:
25×10=250(平方厘米)
7.(1) 13 1300
(2) 12 1200
【分析】(1)根据图示可知,淘气摆的纸箱因为放在墙角处,所以有三面靠墙的在内部,所以露在外部的有:正面5个正方形,右面5个正方形,上面3个正方形,一共有5+5+3=13(个),每个小正方形面的面积是10×10=100(平方厘米),据此再乘13就是露在外部的总面积。
(2)根据图示可知,笑笑摆的纸箱因为放在墙角处,所以有三面靠墙的在内部,所以露在外部的有:正面4个正方形,右面4个正方形,上面4个正方形,一共有4+4+4=12(个),每个小正方形面的面积是10×10=100(平方厘米),据此再乘12就是露在外部的总面积。
(1)
5+5+3=13(个)
10×10×13=1300(平方厘米)
(2)
4+4+4=12(个)
10×10×12=1200(平方厘米)
8.C
【分析】根据题意,露在外面的面一共有10个,一个面的面积为(5×5)cm2,据此用乘法求出10个面的面积即可。
【详解】根据题意得
5×5×10
=25×10
=250(cm2)
露在外面的面积250cm2。
故答案为:C
9.B
【分析】观察图形可知,从上面看到的是4个正方形面,从前面看到是4个正方形面,从右面看到的是4个正方形面,把从上面、右面、前面看到的面相加,可算出总共露出来多少个小正方形,再根据正方形面积公式:S=a×a,求出1个正方形的面积,最后乘正方形的个数即可。
【详解】露出来的正方形总个数为:
4+4+4
=8+4
=12(个)
1个正方形面积为:
5×5=25(cm2)
露在外面的面积是:
25×12=300(cm2)
故答案为:B
10.B
【分析】观察正方体的摆放,第一个图有1×3+2=5(个)面露在外面,第二个图有2×3+2=8(个)面露在外面,第三个图有3×3+2=11(个)面露在外面,那么每增加1个小正方体就增加3个面露在外面。由此解题即可。
【详解】3×7+2
=21+2
=23(个)
所以,将7个按图中的方式摆放在桌面上,有23个面露在外面。
故答案为:B
11.D
【分析】观察图形可知,从正面看,有3个面露在外面;从上面看,有2个面露在外面;从右侧看,有2个面露在外面;一共有3+2+2=7个面露在外面;再根据正方形面积公式:面积=边长×边长,代入数据,求出一个正方形面积,再乘露出外面面的个数,即可解答。
【详解】3+2+2
=5+2
=7(个)
10×10×7
=100×7
=700(平方厘米)
故答案为:D
12.C
【分析】先数清各选项露在外面的面的个数,再根据正方形面积公式:边长×边长,代入数据,求出一个面的面积,再乘露在外面的面的个数,求出露在外面的面的面积,进行比较,即可解答。
【详解】A. 一共有17个面露在外面;面积:1×1×17=17(dm2);
B. 一共有18个面露在外面;面积:1×1×18=18(dm2);
C.一共有19个面露在外面;面积:1×1×19=19(dm2);
D.一共有17个面露在外面,面积:1×1×17=17(dm2)。
故答案为:C
13.C
【分析】看图可知,拿走①或④,减少了三个面,同时又增加了三个面,则图形的表面积没有变;拿走②,减少了两个面,同时又增加了四个面,则图形的表面积增大;拿走③,减少了一个面,同时又增加了五个面,则图形的表面积增大;据此判断即可。
【详解】根据分析可知:若干个完全一样的小正方体拼成一个大正方体。如果从最上面一层拿走①②③④中的一个小正方体(如图),要想剩下的立体图形的表面积与大正方体表面积相等,只能拿走①号或者④。
故答案为:C
14.D
【分析】1个小正体有5个面露在外面,再增加一个正方体,2个小正方体有8个面露在外面;3个小正方体有11个面露在外面.每增加1个正方体漏在外面的面就增加3个即:n个正方体有5+(n-1)×3;由此求解。解答此题应根据题意,进行推导,得出规律:即1个小正方体露出5个面,每增加1个小正方体增加3个面;进行解答即可。
【详解】根据分析可知,6个正方体有:
5+(6-1)×3
=5+5×3
=5+15
=20(个)
故答案为:D
15.C
【分析】观察图形可知,在大正方体的顶点位置去掉一个小正方形,虽然减少了3个小正方形的面积,但产生的切面上又增加了3个小正方形的面积,所以得到图形的表面积与原来正方体的表面积相等。
【详解】通过分析,一个由8个小正方体拼成的大正方体,如果去掉一个小正方体,得到的图形的表面积与原来的表面积相等。
故答案为:C
16.D
【分析】根据正方体拼组长方体的方法,可以将12分解质因数,12=2×2×3,所以12个小正方体拼成的大长方体有:12×1×1、 4×3×1、 2×6×1、2×2×3共四种情况,其中2×2×3减少的面最多,所以拼成的长方体的表面积最小,也可以利用长方体表面积计算公式计算出组合图形的表面积进行比较得出答案。
【详解】假设一个小正方体的棱长是1分米。
选项A的表面积:(1×12+1×12+1×1)×2
=(12+12+1)×2
=25×2
=50(平方分米)
选项B的表面积:(3×1+1×4+3×4)×2
=(3+4+12)×2
=19×2
=38(平方分米)
选项C的表面积:(2×1+1×6+2×6)×2
=(2+6+12)×2
=20×2
=40(平方分米)
选项D的表面积:(2×2+2×3+2×3)×2
=(4+6+6)×2
=16×2
=32(平方分米)
因为32<38<40<50,所以选项B的表面积最小。
故答案为:D
17.D
【分析】把这个长方体截成完全相同的两个小长方体,可以从上面横切,增加的面积是4×1×2=8(平方厘米);可以从上面竖切,增加的面积是3×1×2=6(平方厘米);也可以沿水平方向切,增加的面积是4×3×2=24(平方厘米)。据此解答。
【详解】通过分析可知,把这个长方体沿水平分向切成两个小长方体,表面积之和增加最多,最多增加4×3×2=24(平方厘米)。
故答案为:D
18.√
【分析】分别数出从各个方向看到的这些正方形的面数,相加即可。
【详解】从正面看,可以看到2个正方形;
从右面看,可以看到3个正方形;
从上面看,可以看到5个正方形。
露在外面的面有:
2+3+5
=5+5
=10(个)
故答案为:√
19.×
【分析】大正方体挖去一个小正方体,仔细观察,凹下去图形是4个面的面积,而原来缺失的是2个面的面积,所以大正方体的表面积和以前相比,多了2个面的面积,据此解答。
【详解】根据分析,这个组合体的表面积与之前相比,表面积增加了。所以原题的说法是错误的。
故答案为:×
20.×
【分析】把4个小正方体摆放在一起,摆放的方法有多种。如果4个摆成一排,从上面看有4个面,从前、后看有8个面,左、右各看到1个面,则露在外面的面是4+8+2=14(个);如果再用不同的摆法,露在外面的面的数量也是不同的。
【详解】通过分析可知,不同的摆法,露在外面的面的数量也不同。原题说法错误。
故答案为:×
21.×
【分析】将3个相同的正方体放在墙角处,如图有三种不同的方法:
,数出露在外面的面一共有几个,再进一步解答即可。
【详解】由分析可知:可以摆如下图所示的三种情况。
以上三种直观图露在外面的面都是7个,原说法错误。
故答案为:×
22.×
【分析】在一个正方体的顶点位置挖去一个小正方体,表面积不变;在一个正方体棱的位置挖去一个小正方体,表面积增加;在一个正方体面上挖去一个小正方体,则表面积增加。据此解答。
【详解】在一个正方体的任何一个位置挖去一个小正方体,则表面积会增加或不变。
故答案为:×
23.√
【分析】正方体有6个面,放在空旷的平地上说明只有下面的一个面被挡住了,所以有5个面露在外面。据此判断。
【详解】把一个正方体放置在空旷的平地上,有5个面露在外面。此说法正确,故答案为:正确。
24.(1)5;8;11;14;(2)见详解;(3)32
【分析】(1)观察图形,小正方体的个数为1时,露在外面的面有5个面,小正方体的个数为2时,露在外面的面有(5+3)个面,小正方体的个数为3时,露在外面的面有(5+3×2)个面,小正方体的个数为4时,露在外面的面有(5+3×3)个面,据此完成填空。
(2)通过前面计算出来的数据,我们可以看出随着小正方体的个数的增多,露在外面的面的个数也在增加,具体的变化规律是当前图形露在外面的面的个数比前一个露在外面的面的个数要多3个。
(3)依次类推,小正方体的个数为n时,露在外面的面有个面,当n=10时,把数据代入,即可求出有多少个露在外面的面。
【详解】(1)5+3=8(个)
5+3×2
=5+6
=11(个)
5+3×3
=5+9
=14(个)
填表如下:
小正方体的个数 1 2 3 4
露在外面的面/个 5 8 11 14
(2)答:我发现当前图形露在外面的面的个数比前一个露在外面的面的个数要多3个。
(3)小正方体的个数为n时,露在外面的面有个面,
当n=10时,
=
=
=5+27
=32(个)
25.11个;9900平方厘米
【分析】从上面看,能看到4个面,从正面看,能看到4个面,从右面看,能看到3个面,这样共能够看到4+4+3=11个面,正方体的棱长已知,棱长×棱长求出1个面的面积,再乘11就可以求出露在外面的面积。
【详解】4+4+3
=8+3
=11(个)
30×30×11
=900×11
=9900(平方厘米)
答:露出11个面,露在外面的面积是9900平方厘米。
26.1536cm2;不相等
【分析】4个正方体的表面积之和=棱长×棱长×6×4,将一个由4个棱长是8cm的正方体拼成的长方体拆开,表面积增加了6个面的面积。
【详解】8×8×6×4
=64×6×4
=1536(cm2)
将一个由4个棱长是8cm的正方体拼成的长方体拆开,表面积增加了6个面的面积,与原来长方体的表面积不相等。
答:4个正方体的表面积之和是1536cm2,与长方体的表面积不相等。
27.(1)11个
(2)4400平方厘米
(3)可能不变,也可能会发生变化;因为露在外面的面数不确定
【分析】(1)露在外部的有:正面3个正方形,右面4个正方形,上面4个正方形,一共有3+4+4=11(个);
(2)每个小正方形面的面积是20×20=400(平方厘米),据此再乘11就是露在外部的总面积;
(3)改变摆法,露在外面的面积可能不变,也可能会发生变化,因为露在外面的面数不确定。
【详解】(1)正面3个正方形,右面4个正方形,上面4个正方形,
3+4+4
=7+4
=11(个)
答:有11个面露在外面。
(2)20×20×11
=400×11
=4400(平方厘米)
答:露在外面的面积是4400平方厘米。
(3)改变摆法,露在外面的面积可能不变,也可能会发生变化,因为露在外面的面数不确定。
答案第1页,共2页
答案第1页,共2页
