六年级下册数学 人教版 6.1.9 比和比例(1)(教材P83页例1-例2)课件(共24张PPT)
文档属性
| 名称 | 六年级下册数学 人教版 6.1.9 比和比例(1)(教材P83页例1-例2)课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
人教版数学六年级下册
9.比和比例(1)
(教材P83例1例2)
第六单元 整理和复习
情景导入
1、哪位同学能用“比的知识”说说我们班男同学、女同学和全班人数的关系?
男生和女生人数的比是( )
女生和男生人数的比是( )
女生和全班人数的比是( )
男生和全班人数的比是( )
2、你能再说一个比和黑板上的比组成比例吗?
利用比的基本性质,找到比值相等的两个比,可以组成比例。
情景导入
一、比和比例
两个数相除又叫作两个数的比。
表示两个比相等的式子叫作比例。
探究新知
1、说一说什么是比,什么是比例?
2、比和比例有什么区别和联系?
区别
联系
比表示两个数的相除关系,是一个关系式
比例表示两个比的相等关系,是一个等式
比例由两个相等的比组成
比
比的意义
比的书写形式
比的基本性质
比的应用
求比值
化简比(结果是一个比)
比例
比例的意义
比例的基本性质
用比例解决问题
组比例
解比例
(两个数相除又叫做两个数的比)
(表示两个比相等的式子叫做比例)
(结果是一个数)
解比例
(可以求出比例中未知的一项)
(按比分配)
比例的应用
探究新知
比例的书写形式
(a:b;)
(比的前项和后项同乘和同除以一个不为0的数,比值不变)
(比的两内项之积等于两外项之积)
比的基本性质的利用
比例的基本性质的利用
a:b=c:d
=
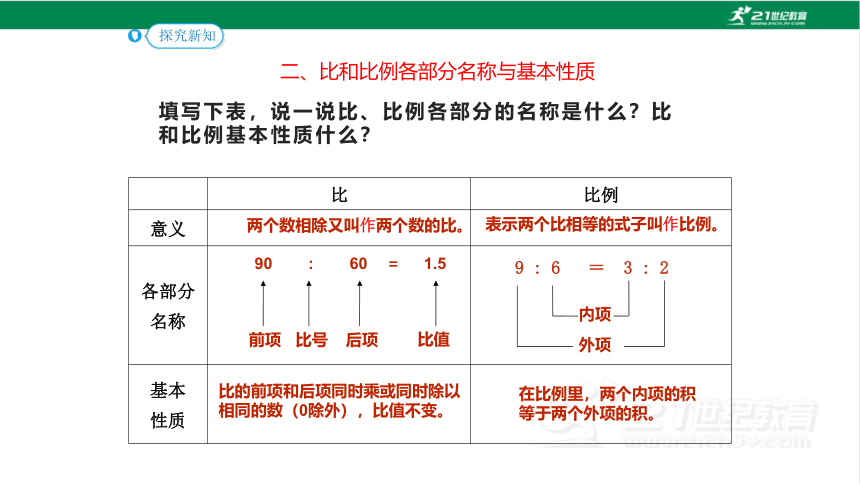
填写下表,说一说比、比例各部分的名称是什么?比和比例基本性质什么?
比 比例
意义
各部分 名称
基本 性质
两个数相除又叫作两个数的比。
表示两个比相等的式子叫作比例。
90 : 60 = 1.5
比值
前项
后项
内项
比号
9 : 6 = 3 : 2
外项
比的前项和后项同时乘或同时除以
相同的数(0除外),比值不变。
在比例里,两个内项的积
等于两个外项的积。
探究新知
二、比和比例各部分名称与基本性质
① 整数比化简,比的前项和后项同时除以它们的最大公因数。
化简比的方法有哪些?
3∶18
15∶18
26∶39
540∶18
探究新知
三、化简比
=1∶6
=5∶6
=30∶1
=2∶3
② 小数比化简,一般是把前项、后项的小数点向右移动相同的位数(位数不够补零),使它成为整数比,再用第一种方法化简。
1.25∶2.5
2.6∶13
1.8∶6
0.25∶0.5
探究新知
=125∶250
=1∶2
=18∶60
=3∶10
=26∶130
=1∶5
=25∶50
=1∶2
③ 分数比化简,一般先把比的前项、后项同时乘上分母的最小公倍数,使它成为整数比,再用第一种方法化简。
6∶
∶
∶
0.4∶
④ 特殊:也可以用求比值的方法化简,求出比值后再写成比的形式。
探究新知
=18∶2
=9∶1
=12∶10
=6∶5
=15∶8
=∶
=6∶10
=3∶5
两个纯分数的比,通过前后项同乘分母的最小公倍数,可化成整数比,事实上等于两个分数分子和分母交叉相乘的比(必须是第一个分数的分子在前项,分母在后项,即先下后上)
带有单位的比化简:先统一单位,再化简
3时∶18分
2.5吨∶1250千克
探究新知
=180分∶18分
180∶18=10:1
=2500千克∶1250千克
2500∶1250=2:1
四、求比值
0.24∶0.06
=24÷6=4
6∶
∶
求出下列比的比值,说一说求比值的方法。
探究新知
=6×=9
= ×=
根据比的意义,用除法可以求出比的比值。比值可以是整数,可以是小数,也可以是分数。
五、解比例
∶
=12∶
=
解:
X:
解:
探究新知
化简比 求比值 解比例
8:0.4
比
------
=80:4
=20:1
8:0.4
= 8÷0.4
= 20
数
------
x:8=3:4
解:4x=3×8
4x=24
x=6
六 、化简比、求比值和解比例的区别
求比例中一个未知项
------
探究新知
1.解比例:
2、求比值:
3、化简比:
=0.625
=0.25
=10
0.7︰0.25
=1︰2
=14︰5
=10︰1
基础练习
4.填空。
(1)把10分︰ 1时化成最简单的整数比是( ),它 的比值是( )。
(2)被减数和减数的比是7 ︰ 3,减数与差的比是
( )。
(3)一个三角形与一个平行四边形等底、等高,三
角形与平行四边形的面积比是( )。
1∶ 6
3 ∶ 4
1 ∶ 2
基础练习
(4)一辆货车5小时行驶240 km,一辆轿车3小时
行驶210 km。
①这辆货车行驶的路程与时间的比是( )。
②这辆轿车行驶的路程与时间的比是( )。
③货车与轿车行驶的路程比是( )。
④货车与轿车行驶的时间比是( )。
48∶1
70∶1
8∶7
5∶3
基础练习
(5)B是A的 ,那么A∶ B=( ) ∶ ( )。
(6)如果A×3=B×5,那么A ∶ B=( )∶( )。
(7)4.5、7.5、 和 组成比例,内项积是( )。
7
5
5
3
2.25
基础练习
5.选择。
(1)大圆的半径是小圆半径的3倍,则小圆面积与大圆面积的比是( )。
A. 1∶3 B. 3∶1 C. 1∶9 D. 9∶1
(2)一项工程,甲独做5天完成,乙独做8天完成,甲、乙的工作效率比为( )。
A. 5∶8 B. 8∶5 C. 1∶2 D. 2∶1
C
B
基础练习
1、李师傅昨天6小时做了72个零件,今天8小时做了96个零件。写出李师傅昨天和今天所做零件个数的比和所用时间的比。这两个比能组成比例吗?为什么?
昨天 72∶ 6=12 ∶ 1
今天 96∶ 8=12 ∶ 1
能组成比例,因为比值一定。
拓展练习
解:设需要分钟,(锯三段需要锯2次,锯6段需要锯5次)
8:2= :5
=40
=20
答:需要20分钟。
2.一根木料锯了3段需要8分钟,如果锯6段需要几分钟?(用比例知识解答)
拓展练习
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版数学六年级下册
9.比和比例(1)
(教材P83例1例2)
第六单元 整理和复习
情景导入
1、哪位同学能用“比的知识”说说我们班男同学、女同学和全班人数的关系?
男生和女生人数的比是( )
女生和男生人数的比是( )
女生和全班人数的比是( )
男生和全班人数的比是( )
2、你能再说一个比和黑板上的比组成比例吗?
利用比的基本性质,找到比值相等的两个比,可以组成比例。
情景导入
一、比和比例
两个数相除又叫作两个数的比。
表示两个比相等的式子叫作比例。
探究新知
1、说一说什么是比,什么是比例?
2、比和比例有什么区别和联系?
区别
联系
比表示两个数的相除关系,是一个关系式
比例表示两个比的相等关系,是一个等式
比例由两个相等的比组成
比
比的意义
比的书写形式
比的基本性质
比的应用
求比值
化简比(结果是一个比)
比例
比例的意义
比例的基本性质
用比例解决问题
组比例
解比例
(两个数相除又叫做两个数的比)
(表示两个比相等的式子叫做比例)
(结果是一个数)
解比例
(可以求出比例中未知的一项)
(按比分配)
比例的应用
探究新知
比例的书写形式
(a:b;)
(比的前项和后项同乘和同除以一个不为0的数,比值不变)
(比的两内项之积等于两外项之积)
比的基本性质的利用
比例的基本性质的利用
a:b=c:d
=
填写下表,说一说比、比例各部分的名称是什么?比和比例基本性质什么?
比 比例
意义
各部分 名称
基本 性质
两个数相除又叫作两个数的比。
表示两个比相等的式子叫作比例。
90 : 60 = 1.5
比值
前项
后项
内项
比号
9 : 6 = 3 : 2
外项
比的前项和后项同时乘或同时除以
相同的数(0除外),比值不变。
在比例里,两个内项的积
等于两个外项的积。
探究新知
二、比和比例各部分名称与基本性质
① 整数比化简,比的前项和后项同时除以它们的最大公因数。
化简比的方法有哪些?
3∶18
15∶18
26∶39
540∶18
探究新知
三、化简比
=1∶6
=5∶6
=30∶1
=2∶3
② 小数比化简,一般是把前项、后项的小数点向右移动相同的位数(位数不够补零),使它成为整数比,再用第一种方法化简。
1.25∶2.5
2.6∶13
1.8∶6
0.25∶0.5
探究新知
=125∶250
=1∶2
=18∶60
=3∶10
=26∶130
=1∶5
=25∶50
=1∶2
③ 分数比化简,一般先把比的前项、后项同时乘上分母的最小公倍数,使它成为整数比,再用第一种方法化简。
6∶
∶
∶
0.4∶
④ 特殊:也可以用求比值的方法化简,求出比值后再写成比的形式。
探究新知
=18∶2
=9∶1
=12∶10
=6∶5
=15∶8
=∶
=6∶10
=3∶5
两个纯分数的比,通过前后项同乘分母的最小公倍数,可化成整数比,事实上等于两个分数分子和分母交叉相乘的比(必须是第一个分数的分子在前项,分母在后项,即先下后上)
带有单位的比化简:先统一单位,再化简
3时∶18分
2.5吨∶1250千克
探究新知
=180分∶18分
180∶18=10:1
=2500千克∶1250千克
2500∶1250=2:1
四、求比值
0.24∶0.06
=24÷6=4
6∶
∶
求出下列比的比值,说一说求比值的方法。
探究新知
=6×=9
= ×=
根据比的意义,用除法可以求出比的比值。比值可以是整数,可以是小数,也可以是分数。
五、解比例
∶
=12∶
=
解:
X:
解:
探究新知
化简比 求比值 解比例
8:0.4
比
------
=80:4
=20:1
8:0.4
= 8÷0.4
= 20
数
------
x:8=3:4
解:4x=3×8
4x=24
x=6
六 、化简比、求比值和解比例的区别
求比例中一个未知项
------
探究新知
1.解比例:
2、求比值:
3、化简比:
=0.625
=0.25
=10
0.7︰0.25
=1︰2
=14︰5
=10︰1
基础练习
4.填空。
(1)把10分︰ 1时化成最简单的整数比是( ),它 的比值是( )。
(2)被减数和减数的比是7 ︰ 3,减数与差的比是
( )。
(3)一个三角形与一个平行四边形等底、等高,三
角形与平行四边形的面积比是( )。
1∶ 6
3 ∶ 4
1 ∶ 2
基础练习
(4)一辆货车5小时行驶240 km,一辆轿车3小时
行驶210 km。
①这辆货车行驶的路程与时间的比是( )。
②这辆轿车行驶的路程与时间的比是( )。
③货车与轿车行驶的路程比是( )。
④货车与轿车行驶的时间比是( )。
48∶1
70∶1
8∶7
5∶3
基础练习
(5)B是A的 ,那么A∶ B=( ) ∶ ( )。
(6)如果A×3=B×5,那么A ∶ B=( )∶( )。
(7)4.5、7.5、 和 组成比例,内项积是( )。
7
5
5
3
2.25
基础练习
5.选择。
(1)大圆的半径是小圆半径的3倍,则小圆面积与大圆面积的比是( )。
A. 1∶3 B. 3∶1 C. 1∶9 D. 9∶1
(2)一项工程,甲独做5天完成,乙独做8天完成,甲、乙的工作效率比为( )。
A. 5∶8 B. 8∶5 C. 1∶2 D. 2∶1
C
B
基础练习
1、李师傅昨天6小时做了72个零件,今天8小时做了96个零件。写出李师傅昨天和今天所做零件个数的比和所用时间的比。这两个比能组成比例吗?为什么?
昨天 72∶ 6=12 ∶ 1
今天 96∶ 8=12 ∶ 1
能组成比例,因为比值一定。
拓展练习
解:设需要分钟,(锯三段需要锯2次,锯6段需要锯5次)
8:2= :5
=40
=20
答:需要20分钟。
2.一根木料锯了3段需要8分钟,如果锯6段需要几分钟?(用比例知识解答)
拓展练习
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
