六年级下册数学 人教版 6.2.2 图形的认识与测量(二)(教材P86页例3)课件(共35张PPT)
文档属性
| 名称 | 六年级下册数学 人教版 6.2.2 图形的认识与测量(二)(教材P86页例3)课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 20:49:54 | ||
图片预览






文档简介
(共35张PPT)
人教版数学六年级下册
2.图形的认识与测量(二)
(教材P86例3)
第六单元 整理和复习
复习旧知
什么是面积单位?我们学过哪些面积单位?
平面图形的周长和面积
周长:封闭图形一周的总长度。
2、我们学过的平面图形有哪些?
3、想一想,这些图形的周长和面积公式是怎样推导的?
面积: 物体表面的大小或物体所占平面的大小,叫做面积。
用割补的方法,用转化的思想。
探究新知
1、什么是周长,什么是面积?
长方形、正方形、平行四边形、三角形、梯形、圆
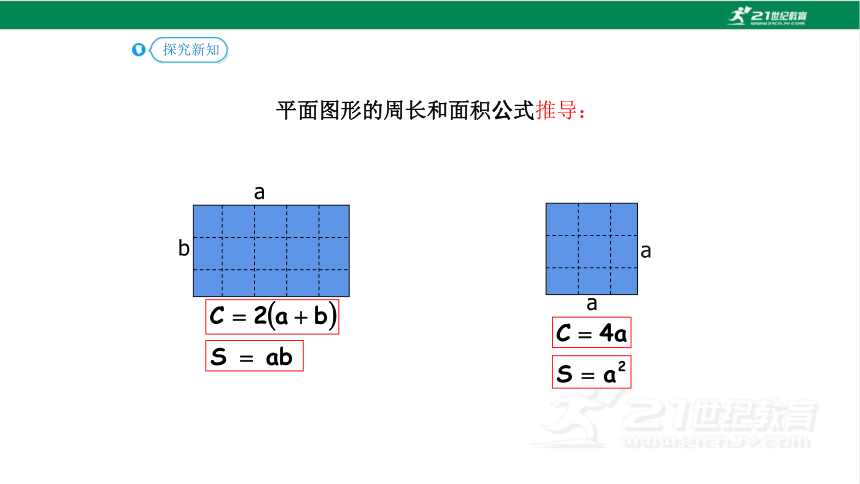
a
b
a
a
平面图形的周长和面积公式推导:
探究新知
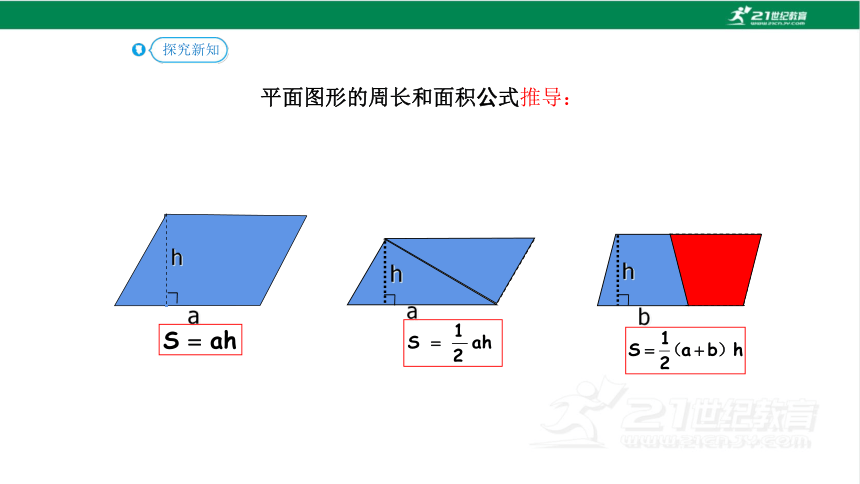
a
h
a
h
b
h
平面图形的周长和面积公式推导:
探究新知
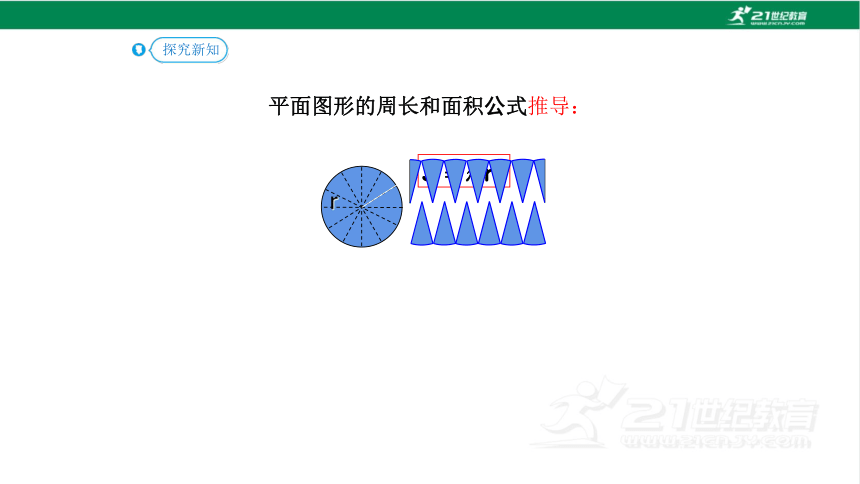
r
平面图形的周长和面积公式推导:
探究新知
平行四边形:
长方形:
三角形:
梯形:
说说我们学过的平面图形周长、面积的计算公式:
正方形:
探究新知
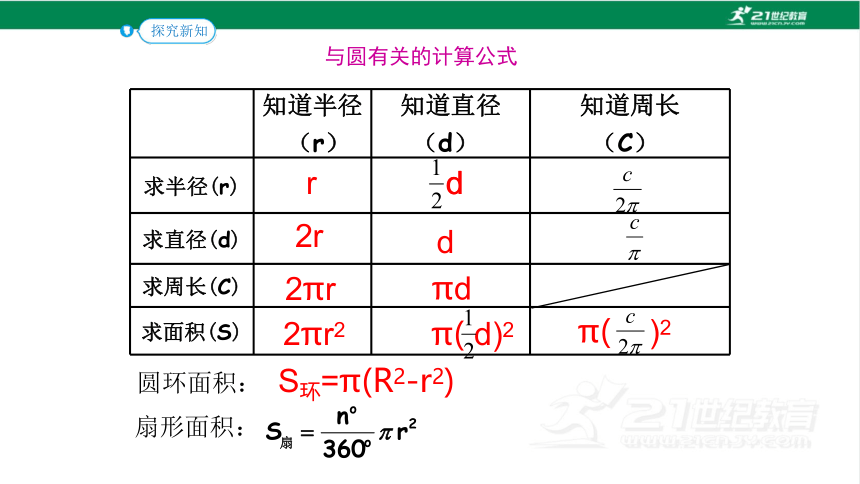
知道半径 (r) 知道直径 (d) 知道周长
(C)
求半径(r)
求直径(d)
求周长(C)
求面积(S)
与圆有关的计算公式
圆环面积:
扇形面积:
探究新知
r
2r
2πr
2πr2
d
d
πd
π( d)2
d
S环=π(R2-r2)
π( )2
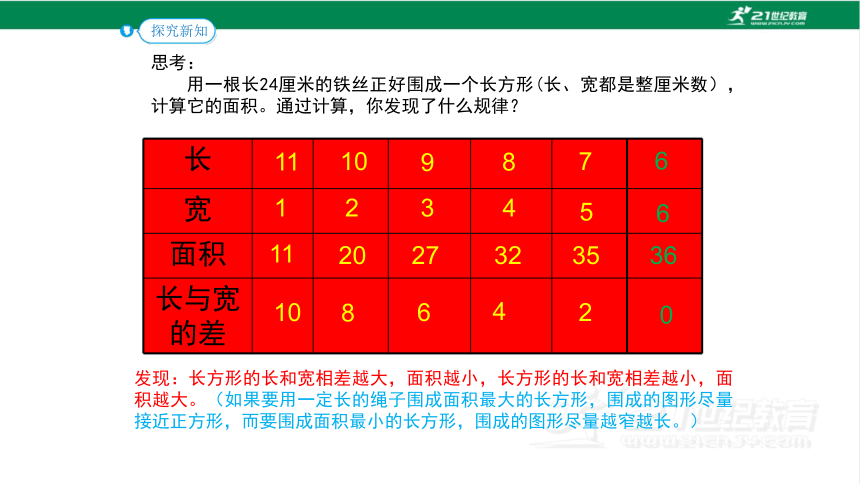
思考:
用一根长24厘米的铁丝正好围成一个长方形(长、宽都是整厘米数),计算它的面积。通过计算,你发现了什么规律?
长
宽
面积
长与宽的差
探究新知
1
11
2
10
11
10
20
8
3
9
27
6
4
8
32
4
5
7
35
2
6
6
36
0
发现:长方形的长和宽相差越大,面积越小,长方形的长和宽相差越小,面积越大。(如果要用一定长的绳子围成面积最大的长方形,围成的图形尽量接近正方形,而要围成面积最小的长方形,围成的图形尽量越窄越长。)
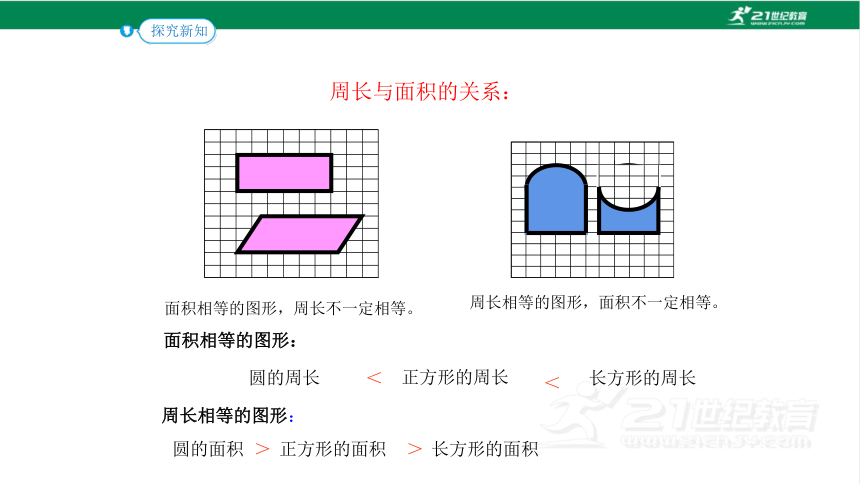
周长相等的图形,面积不一定相等。
周长与面积的关系:
面积相等的图形,周长不一定相等。
面积相等的图形:
圆的周长
<
正方形的周长
长方形的周长
<
周长相等的图形:
圆的面积
>
正方形的面积
>
长方形的面积
探究新知
1π=3.14
常用的计算数据(一)
2π=6.28
3π=9.42
4π=12.56
5π=15.7
6π=18.84
7π=21.98
8π=25.12
9π=28.26
16π=50.24
25π=78.5
36π=113.04
64π=200.96
15π=47.1
102=100
112=121
122=144
132=169
142=196
152=225
225π=706.5
162=256
172=289
182=324
192=361
202=400
252=625
探究新知
1、圆周长的一半=c÷2=πr
2、半圆的周长=πr+2r
3、半圆的面积=s ÷2
4、环形的面积=π(R —r )
探究新知
常用的计算数据(二)
2、两个完全重合的三角形可以拼成一个平行四边形,等底等高的平行四边形等于三角形面积的2倍;等底等高的三角形等于平行四边形面积的一半。
1、等底等高的平行四边形面积相等。
3、两个完全重合的梯形可以拼成一个平行四边形。
探究新知
常用的计算数据(三)
1、轴对称图形:沿一条直线对折,两边能完全重合的图形叫轴对称图形。
2、一条对称轴的图形有:等腰三角形、等腰梯形,半圆
3、两条对称轴的图形有:长方形
4、三条对称轴的图形有:等边三角形
5、四条对称轴的图形有:正方形
6、无数条对称轴的图形有:圆
轴对称图形常识
探究新知
一、计算下面图形的面积。(单位:m)
基础练习
20×20 ÷2=200(平方米)
(6+10.5)×6 ÷2=49.5(平方米)
3.14 ×(5 ÷ 2)2 ÷2+5 ×3=24.8125(平方米)
1、面积相等的两个梯形一定可以拼成一个平行四边形。 ( )
2、面积相等的两个三角形形状也相同。( )
3、同底等高的两个三角形的面积一定相等。( )
4、周长相等的长方形和平行四边形,他们的面积一定相等。( )
5、底和高都是0.2厘米的三角形的面积是0.2平方厘米。( )
×
×
√
×
×
二、判断:
基础练习
6、平行四边形的底越长,它的面积就越大。( )
7、三角形的面积是平行四边形面积的一半。( )
8、两个三角形的高相等,它们的面积就相等。( )
9、大于90°的角叫钝角。( )
10、角的两条边越长,角就越大。( )
11、钟表的分针旋转一周,时针旋转30°。( )
12、可以画一条长10厘米的直线。( )
13、用3根长度分别是8厘米、12厘米、3厘米的小棒,能围成一个三角形。( )
×
×
×
√
×
√
×
×
基础练习
14、平角就是一条直线。( )
15、任意一个三角形的三个内角的和都是180°。( )
16、任意的三条线段都可以围成一个三角形。( )
17、每个三角形至少有2个锐角。( )
18、有一组对边平行的四边形是梯形。( )
19、两端都在圆上的线段是直径。( )
×
×
√
×
√
×
基础练习
20、两个半圆一定能拼成一个圆。 ( )
21、半径是2厘米的圆,周长和面积相等。( )
22、大圆的圆周率比小圆的圆周率大。( )
23、半圆形纸片的周长就是圆周长的一半。( )
24、把半径3厘米的圆等分成十六份,拼成一个近似的长方形,长方形的周长比圆的周长长。 ( )
×
×
×
×
√
基础练习
25、在同一个圆内只能画100条直径。( )
26、所有的圆的直径都相等。( )
27、等圆的半径都相等。( )
28、两端都在圆上的线段叫做直径。( )
29、圆心到圆上任意一点的距离都相等( )
30、半径是2厘米的圆比直径是3厘米的圆大。( )
√
×
×
√
√
×
基础练习
1、圆是( )图形,有( )条对称轴。
2、把圆规的两脚分开,定好两脚间的距离作为( )。
3、圆是平面上的一种( )图形。圆的两条直径的交点是圆的( )。
轴对称
半径
无数
曲线
圆心
拓展练习
4、把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
5、周长相等的圆、正方形和长方形,( )的面积最大。
6、圆中最长的线段是圆的( )。
7、把一个直径是10厘米的圆剪成两个半圆,则两个半圆周长的和是( )厘米。
不变
增加
圆
直径
51.4
三、填空
8、用圆规画一个周长12.56厘米的圆,圆规两脚之间的距离是( )厘米,所画圆的面积是( )平方厘米。
9、圆的半径扩大3倍,直径扩大( )倍,周长扩大( )倍;面积扩大( )倍。
10、小铁环直径6分米,大铁环直径8分米。小铁环和大铁环半径的比是( );周长的比是( );面积的比是( )。如果它们滚过相同的路程,则转动的圈数的比是( )。
11、在一张长60厘米,宽40厘米的长方形纸上剪一个最大的圆,则圆的面积是( )平方厘米。
2
12.56
3
3
9
3:4
3:4
9:16
4:3
1256
拓展练习
12、三角形的一个内角正好等于其余两个内角的和,这是一个( )三角形。
13、一个等腰三角形,它的顶角是72 ,它的底角是( )度。18、6时整,时针与分针组成的角的度数是( )。
14、一个等腰三角形的两条边分别是5厘米和8厘米,那么它的周长最多是( )厘米,最少是( )厘米。
15、用360厘米长的铁丝围成一个三角形,三条边长度的比是1:2:3,它的三条边的长度分别是( )、( )和( )厘米。
直角
54
180o
21
1 8
60
120
180
拓展练习
16、工人叔叔把电线杆上的线架和自行车架子做成三角形,这是应用了三角形具有( )的特性,而推拉或防盗门则是由许多小平行四边形组成的,这是应用平行四边形( )的特性。
17、三角形三个角度数的比是2:4:3,最大的角是( )。
不易变形
容易变形
80°
18、一个直角三角形的三条边分别长6厘米、8厘米和10厘米。这个三角形的面积是( )平方厘米。
19、一个正方形周长是1.2米,它的面积是( )平方米。
20、一个等腰三角形的两条边分别是2厘米和5厘米,这个等腰三角形的周长是( )厘米。
24
0.09
12
拓展练习
21、一个平角按4∶5分成两个角。这两个角的度数分别是( )和( )。
22、一个直角三角形的一个锐角是35度,另一个锐角是( )度。
23、角的两边都是( )线。角的大小与( )有关,与( )无关。
80°
100°
55
射
边的长短
两边开叉的大小
拓展练习
1、周长相等的长方形、正方形和圆中,( )的面积最小。
A、长方形 B、正方形 C、圆
2、把用木条钉成的长方形拉成平行四边形,比较它们的周长和面积。( )
A、周长和面积都变化 B、面积变化,周长不变
C、周长变化,面积不变
3、用一根长16厘米的铁丝围成一个长方形,如果长和宽都是质数,它的面积是( )平方厘米。
A、6 B、10 C、15 D、21
A
B
C
四、选择
拓展练习
4、人们常用三角形的( )性生产自行车大梁,运用平行四边 形的( )性制造电动大门。
A.稳定性 B.易变形 C.平衡性
5、圆的半径扩大2倍,则它的直径扩大( ),面积扩大( )。
A.2倍 B.4倍 C.8倍
A
B
A
B
6、一个平行四边形和一个三角形等底等高,已知平行四边形的面积是25平方厘米,三角形的面积是( )平方厘米。
A. 12.5 B. 25 C. 50
7、一个长方形的长和宽各增加4厘米,它增加的面积( )。
A.等于16平方厘米 B. 小于16平方厘米 C. 大于16平方厘米
A
C
拓展练习
1、把一个圆分割拼成一个近似的长方形,长方形的周长比圆的周长多10厘米,求圆的面积。
3.14×(10÷2)2
=3.14×52
=3.14×25
=78.5(cm2)
拓展练习
五、解决问题
2、一块周长为120米的正方形地与一块三角形地的面积相等,三角形地的底为60米,三角形地的高是多少?
正方形的边长为:120÷4=30(m)
三角形的面积为:30×30=900 (m2)
三角形的高为:900×2÷60=30(m)
答:三角形地的高为30米。
拓展练习
3、一块长方形的铁板,长15米,宽是长的 ,要在这块铁板上截一个最大的圆,这个圆的面积是多少平方米?
长方形的宽为:
圆的半径为:10÷2=5(m)
圆的面积为:52×3.14=78.5(m2)
答:圆的面积是78.5平方米。
拓展练习
4. 求涂色部分的面积。(单位:cm)
提问1:要求涂色部分的面积,你会做吗?请你先试着做一做,看看你都能想到哪些不同的方法?
4
4
8
预设1:梯形面积―三角形面积 (4+12)×4÷2-4×4÷2
预设2:大梯形面积 (4+8)×4÷2
预设3:小三角形面积+大三角形面积 4×4÷2+8×4÷2
提问2:你能读懂他们的想法吗?指名解读同伴的想法。
拓展练习
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版数学六年级下册
2.图形的认识与测量(二)
(教材P86例3)
第六单元 整理和复习
复习旧知
什么是面积单位?我们学过哪些面积单位?
平面图形的周长和面积
周长:封闭图形一周的总长度。
2、我们学过的平面图形有哪些?
3、想一想,这些图形的周长和面积公式是怎样推导的?
面积: 物体表面的大小或物体所占平面的大小,叫做面积。
用割补的方法,用转化的思想。
探究新知
1、什么是周长,什么是面积?
长方形、正方形、平行四边形、三角形、梯形、圆
a
b
a
a
平面图形的周长和面积公式推导:
探究新知
a
h
a
h
b
h
平面图形的周长和面积公式推导:
探究新知
r
平面图形的周长和面积公式推导:
探究新知
平行四边形:
长方形:
三角形:
梯形:
说说我们学过的平面图形周长、面积的计算公式:
正方形:
探究新知
知道半径 (r) 知道直径 (d) 知道周长
(C)
求半径(r)
求直径(d)
求周长(C)
求面积(S)
与圆有关的计算公式
圆环面积:
扇形面积:
探究新知
r
2r
2πr
2πr2
d
d
πd
π( d)2
d
S环=π(R2-r2)
π( )2
思考:
用一根长24厘米的铁丝正好围成一个长方形(长、宽都是整厘米数),计算它的面积。通过计算,你发现了什么规律?
长
宽
面积
长与宽的差
探究新知
1
11
2
10
11
10
20
8
3
9
27
6
4
8
32
4
5
7
35
2
6
6
36
0
发现:长方形的长和宽相差越大,面积越小,长方形的长和宽相差越小,面积越大。(如果要用一定长的绳子围成面积最大的长方形,围成的图形尽量接近正方形,而要围成面积最小的长方形,围成的图形尽量越窄越长。)
周长相等的图形,面积不一定相等。
周长与面积的关系:
面积相等的图形,周长不一定相等。
面积相等的图形:
圆的周长
<
正方形的周长
长方形的周长
<
周长相等的图形:
圆的面积
>
正方形的面积
>
长方形的面积
探究新知
1π=3.14
常用的计算数据(一)
2π=6.28
3π=9.42
4π=12.56
5π=15.7
6π=18.84
7π=21.98
8π=25.12
9π=28.26
16π=50.24
25π=78.5
36π=113.04
64π=200.96
15π=47.1
102=100
112=121
122=144
132=169
142=196
152=225
225π=706.5
162=256
172=289
182=324
192=361
202=400
252=625
探究新知
1、圆周长的一半=c÷2=πr
2、半圆的周长=πr+2r
3、半圆的面积=s ÷2
4、环形的面积=π(R —r )
探究新知
常用的计算数据(二)
2、两个完全重合的三角形可以拼成一个平行四边形,等底等高的平行四边形等于三角形面积的2倍;等底等高的三角形等于平行四边形面积的一半。
1、等底等高的平行四边形面积相等。
3、两个完全重合的梯形可以拼成一个平行四边形。
探究新知
常用的计算数据(三)
1、轴对称图形:沿一条直线对折,两边能完全重合的图形叫轴对称图形。
2、一条对称轴的图形有:等腰三角形、等腰梯形,半圆
3、两条对称轴的图形有:长方形
4、三条对称轴的图形有:等边三角形
5、四条对称轴的图形有:正方形
6、无数条对称轴的图形有:圆
轴对称图形常识
探究新知
一、计算下面图形的面积。(单位:m)
基础练习
20×20 ÷2=200(平方米)
(6+10.5)×6 ÷2=49.5(平方米)
3.14 ×(5 ÷ 2)2 ÷2+5 ×3=24.8125(平方米)
1、面积相等的两个梯形一定可以拼成一个平行四边形。 ( )
2、面积相等的两个三角形形状也相同。( )
3、同底等高的两个三角形的面积一定相等。( )
4、周长相等的长方形和平行四边形,他们的面积一定相等。( )
5、底和高都是0.2厘米的三角形的面积是0.2平方厘米。( )
×
×
√
×
×
二、判断:
基础练习
6、平行四边形的底越长,它的面积就越大。( )
7、三角形的面积是平行四边形面积的一半。( )
8、两个三角形的高相等,它们的面积就相等。( )
9、大于90°的角叫钝角。( )
10、角的两条边越长,角就越大。( )
11、钟表的分针旋转一周,时针旋转30°。( )
12、可以画一条长10厘米的直线。( )
13、用3根长度分别是8厘米、12厘米、3厘米的小棒,能围成一个三角形。( )
×
×
×
√
×
√
×
×
基础练习
14、平角就是一条直线。( )
15、任意一个三角形的三个内角的和都是180°。( )
16、任意的三条线段都可以围成一个三角形。( )
17、每个三角形至少有2个锐角。( )
18、有一组对边平行的四边形是梯形。( )
19、两端都在圆上的线段是直径。( )
×
×
√
×
√
×
基础练习
20、两个半圆一定能拼成一个圆。 ( )
21、半径是2厘米的圆,周长和面积相等。( )
22、大圆的圆周率比小圆的圆周率大。( )
23、半圆形纸片的周长就是圆周长的一半。( )
24、把半径3厘米的圆等分成十六份,拼成一个近似的长方形,长方形的周长比圆的周长长。 ( )
×
×
×
×
√
基础练习
25、在同一个圆内只能画100条直径。( )
26、所有的圆的直径都相等。( )
27、等圆的半径都相等。( )
28、两端都在圆上的线段叫做直径。( )
29、圆心到圆上任意一点的距离都相等( )
30、半径是2厘米的圆比直径是3厘米的圆大。( )
√
×
×
√
√
×
基础练习
1、圆是( )图形,有( )条对称轴。
2、把圆规的两脚分开,定好两脚间的距离作为( )。
3、圆是平面上的一种( )图形。圆的两条直径的交点是圆的( )。
轴对称
半径
无数
曲线
圆心
拓展练习
4、把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
5、周长相等的圆、正方形和长方形,( )的面积最大。
6、圆中最长的线段是圆的( )。
7、把一个直径是10厘米的圆剪成两个半圆,则两个半圆周长的和是( )厘米。
不变
增加
圆
直径
51.4
三、填空
8、用圆规画一个周长12.56厘米的圆,圆规两脚之间的距离是( )厘米,所画圆的面积是( )平方厘米。
9、圆的半径扩大3倍,直径扩大( )倍,周长扩大( )倍;面积扩大( )倍。
10、小铁环直径6分米,大铁环直径8分米。小铁环和大铁环半径的比是( );周长的比是( );面积的比是( )。如果它们滚过相同的路程,则转动的圈数的比是( )。
11、在一张长60厘米,宽40厘米的长方形纸上剪一个最大的圆,则圆的面积是( )平方厘米。
2
12.56
3
3
9
3:4
3:4
9:16
4:3
1256
拓展练习
12、三角形的一个内角正好等于其余两个内角的和,这是一个( )三角形。
13、一个等腰三角形,它的顶角是72 ,它的底角是( )度。18、6时整,时针与分针组成的角的度数是( )。
14、一个等腰三角形的两条边分别是5厘米和8厘米,那么它的周长最多是( )厘米,最少是( )厘米。
15、用360厘米长的铁丝围成一个三角形,三条边长度的比是1:2:3,它的三条边的长度分别是( )、( )和( )厘米。
直角
54
180o
21
1 8
60
120
180
拓展练习
16、工人叔叔把电线杆上的线架和自行车架子做成三角形,这是应用了三角形具有( )的特性,而推拉或防盗门则是由许多小平行四边形组成的,这是应用平行四边形( )的特性。
17、三角形三个角度数的比是2:4:3,最大的角是( )。
不易变形
容易变形
80°
18、一个直角三角形的三条边分别长6厘米、8厘米和10厘米。这个三角形的面积是( )平方厘米。
19、一个正方形周长是1.2米,它的面积是( )平方米。
20、一个等腰三角形的两条边分别是2厘米和5厘米,这个等腰三角形的周长是( )厘米。
24
0.09
12
拓展练习
21、一个平角按4∶5分成两个角。这两个角的度数分别是( )和( )。
22、一个直角三角形的一个锐角是35度,另一个锐角是( )度。
23、角的两边都是( )线。角的大小与( )有关,与( )无关。
80°
100°
55
射
边的长短
两边开叉的大小
拓展练习
1、周长相等的长方形、正方形和圆中,( )的面积最小。
A、长方形 B、正方形 C、圆
2、把用木条钉成的长方形拉成平行四边形,比较它们的周长和面积。( )
A、周长和面积都变化 B、面积变化,周长不变
C、周长变化,面积不变
3、用一根长16厘米的铁丝围成一个长方形,如果长和宽都是质数,它的面积是( )平方厘米。
A、6 B、10 C、15 D、21
A
B
C
四、选择
拓展练习
4、人们常用三角形的( )性生产自行车大梁,运用平行四边 形的( )性制造电动大门。
A.稳定性 B.易变形 C.平衡性
5、圆的半径扩大2倍,则它的直径扩大( ),面积扩大( )。
A.2倍 B.4倍 C.8倍
A
B
A
B
6、一个平行四边形和一个三角形等底等高,已知平行四边形的面积是25平方厘米,三角形的面积是( )平方厘米。
A. 12.5 B. 25 C. 50
7、一个长方形的长和宽各增加4厘米,它增加的面积( )。
A.等于16平方厘米 B. 小于16平方厘米 C. 大于16平方厘米
A
C
拓展练习
1、把一个圆分割拼成一个近似的长方形,长方形的周长比圆的周长多10厘米,求圆的面积。
3.14×(10÷2)2
=3.14×52
=3.14×25
=78.5(cm2)
拓展练习
五、解决问题
2、一块周长为120米的正方形地与一块三角形地的面积相等,三角形地的底为60米,三角形地的高是多少?
正方形的边长为:120÷4=30(m)
三角形的面积为:30×30=900 (m2)
三角形的高为:900×2÷60=30(m)
答:三角形地的高为30米。
拓展练习
3、一块长方形的铁板,长15米,宽是长的 ,要在这块铁板上截一个最大的圆,这个圆的面积是多少平方米?
长方形的宽为:
圆的半径为:10÷2=5(m)
圆的面积为:52×3.14=78.5(m2)
答:圆的面积是78.5平方米。
拓展练习
4. 求涂色部分的面积。(单位:cm)
提问1:要求涂色部分的面积,你会做吗?请你先试着做一做,看看你都能想到哪些不同的方法?
4
4
8
预设1:梯形面积―三角形面积 (4+12)×4÷2-4×4÷2
预设2:大梯形面积 (4+8)×4÷2
预设3:小三角形面积+大三角形面积 4×4÷2+8×4÷2
提问2:你能读懂他们的想法吗?指名解读同伴的想法。
拓展练习
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
