六年级下册数学 人教版 6.4.1 数学思考(1)(教材P99例1)课件(共21张PPT)
文档属性
| 名称 | 六年级下册数学 人教版 6.4.1 数学思考(1)(教材P99例1)课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 20:58:35 | ||
图片预览




文档简介
(共21张PPT)
人教版数学六年级下册
1.数学思考(1)
(教材P99例1)
第六单元 整理和复习
1、根据数的变化规律填数。
13、11、9、( )、( )、( )。
7
5
3
3、1+2+3+4+5+6+...+15+16+17+18+19+20 =
210
( 1 + 20 ) ×20 ÷ 2 = 210
复习导入
2、根据珠子的排列规律,接着画。
培养同学们归纳、推理、探索规律的能力。
渗透“化难为易”的数学思想方法,能运用一定的规律解决较复杂的数学问题。
复习导入
同学们,我们来做一个游戏,请你们拿出纸和笔在纸上任意点上8个点,并将它们每两点连成一条线,再数一数,看看连成了多少条线段。
复习导入
1.从2个点开始连,逐渐增加点数,找一找规律。
2.边连边按要求填表。
3.通过表中的数据你能发现什么规律?
探究新知
一、探究模式的策略
A
B
C
D
探究新知
图形 点数
增加条数
总条 数
2
3
2
3
4
3
6
5
4
10
E
F
6
5
15
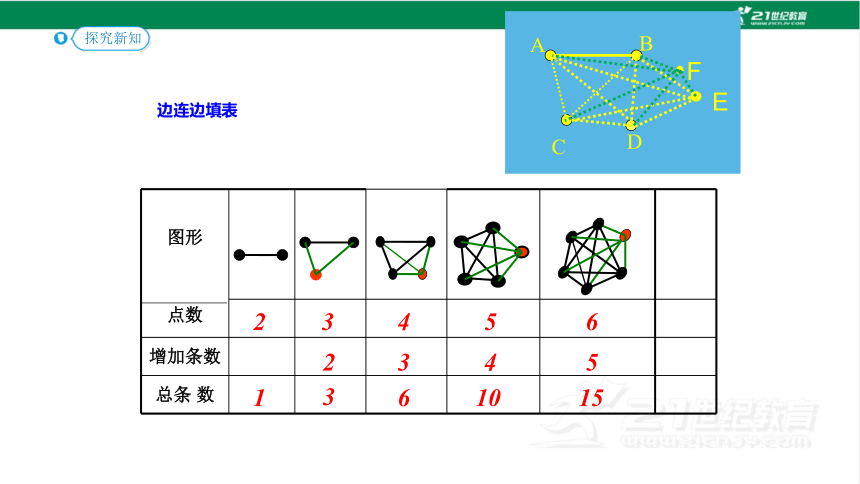
边连边填表
1
图形 点数
增加条数
总条 数
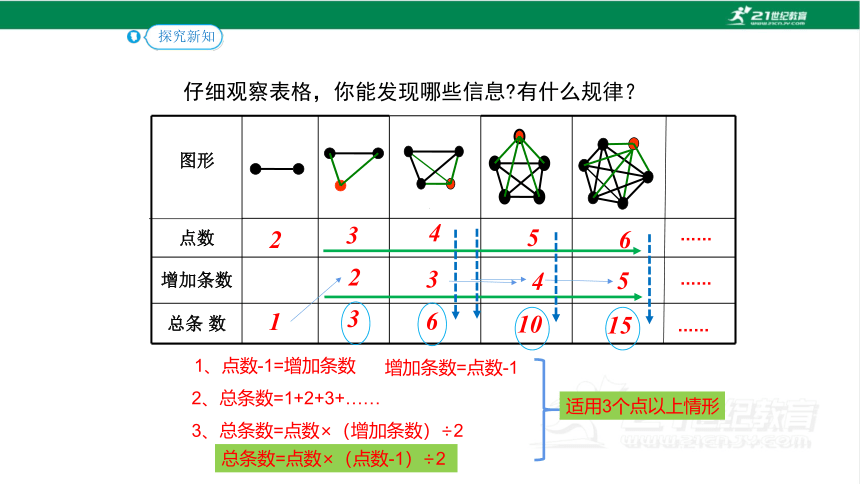
仔细观察表格,你能发现哪些信息 有什么规律?
2
1
3
2
3
4
3
6
5
4
10
6
5
15
……
……
……
探究新知
1、点数-1=增加条数
2、总条数=1+2+3+……
增加条数=点数-1
3、总条数=点数×(增加条数)÷2
适用3个点以上情形
总条数=点数×(点数-1)÷2
图形 点数
增加条数
总条 数
仔细观察表格,你能发现哪些信息 有什么规律?
2
1
3
2
3
4
3
6
5
4
10
6
5
15
……
……
……
探究新知
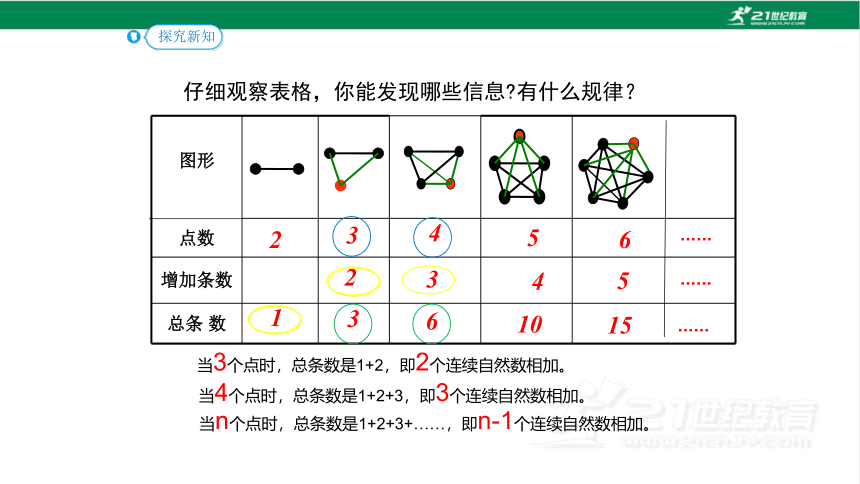
当3个点时,总条数是1+2,即2个连续自然数相加。
当4个点时,总条数是1+2+3,即3个连续自然数相加。
当n个点时,总条数是1+2+3+……,即n-1个连续自然数相加。
A
E
D
C
B
已连接
已连接
已连接
已连接
已连接
已连接
全部已连接
探究新知
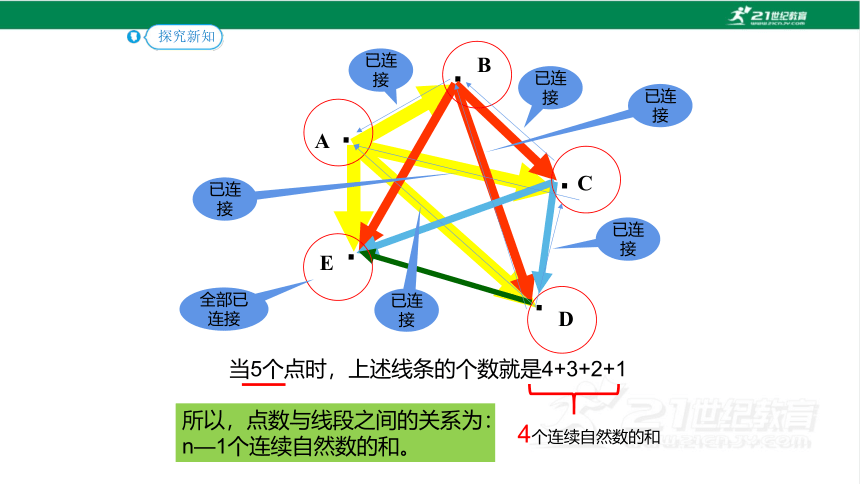
当5个点时,上述线条的个数就是4+3+2+1
4个连续自然数的和
所以,点数与线段之间的关系为:
n—1个连续自然数的和。
探究新知
1、同学们还记得连续自然数相加的求和公式吗?
1+2+3+4+……+n=n×(n+1)÷2
2、通过上面三种方法的观察,当有n个点时,它的总条 数是n-1个连续自然数的和,那么我们能不能根据点数来求出线段总条数呢?
把上面的n换成n-1试试看。
n×(n+1)÷2
(n-1)×[(n-1)+1)]÷2
(n-1)×n÷2
n× (n-1) ÷2
探究新知
我们也可以这样来理解:
n-1个连续自然数的和,可以先算n个连续自然数的和,然后再减n本身。
n×(n+1)÷2-n
=n×[(n+1)÷2-1]
=n× (+)
=n× ( - )
=n× (n-1)÷2
探究新知
连接7个点,会连成多少条线段?12个点,25个点呢?
总条数=点数×(点数-1)÷2
总条数=7×(7-1)÷2=21
总条数=12×(12-1)÷2=66
总条数=25×(25-1)÷2=300
同学们,在我们生活中有许多看似复杂的问题,我们都可以尝试从简单问题去思考,逐步找到其中的规律,从而来解决复杂的问题。
遇到复杂的问题的处理方法
3. 有序思考
2. 画图、枚举
1. 化繁为简
4. 探究规律
探究新知
基础练习
一、填空
1、6个点可以连成线段的条数是( )。
2、1,3,2,6,4,( ),( ),12,( )。
3、按规律填数:3、15、35、63、99、( )、195。
4、 一个长方形被剪去一个角后,还剩( )个角或( )个角,或( )个角。
15
9
8
16
奇数位上的数后一个是前一个的2倍
偶数位上的数后一个比前一个多3
143
连续奇数的积。
5
4
3
2、想一想,算一算:
寒假过去了,10个好朋友见面了,每两位好朋友握手一次,请同学们帮忙算算,他们一共握了多少次手?
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45(次)
答:一共握了45次手。
10 × (10 - 1) ÷ 2 = 45 (次)
( 1 + 9 ) × 9 ÷ 2 = 45 (次)
基础练习
n×(n+1)÷2(连续自然数求和公式)
n×(n-1)÷2
拓展练习
1、某小学开展秋季球类运动会,学校一共有8个篮球运动队,比赛采取对对见面的方式,你能不能算一下,第一轮比赛需要打几场球赛?
8×(8-1)÷2=28(场)
7+6+5+4+3+2+1=7×(7+1)÷2=28(场)
答:第一轮比赛需要打28场比赛。
拓展练习
2、用3,4,5,6四张数字卡片,每次取两张组成一个两位数,可以组成多少个偶数?
十位
个位
可填4个数
每个十位数据后可填3个数
4
×
3
=12
一共可以组成12个数。
十位
个位
可填2个数
每个个位数字前面可填3个数
3
×
2
=6
一共可以组成6个偶数。
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版数学六年级下册
1.数学思考(1)
(教材P99例1)
第六单元 整理和复习
1、根据数的变化规律填数。
13、11、9、( )、( )、( )。
7
5
3
3、1+2+3+4+5+6+...+15+16+17+18+19+20 =
210
( 1 + 20 ) ×20 ÷ 2 = 210
复习导入
2、根据珠子的排列规律,接着画。
培养同学们归纳、推理、探索规律的能力。
渗透“化难为易”的数学思想方法,能运用一定的规律解决较复杂的数学问题。
复习导入
同学们,我们来做一个游戏,请你们拿出纸和笔在纸上任意点上8个点,并将它们每两点连成一条线,再数一数,看看连成了多少条线段。
复习导入
1.从2个点开始连,逐渐增加点数,找一找规律。
2.边连边按要求填表。
3.通过表中的数据你能发现什么规律?
探究新知
一、探究模式的策略
A
B
C
D
探究新知
图形 点数
增加条数
总条 数
2
3
2
3
4
3
6
5
4
10
E
F
6
5
15
边连边填表
1
图形 点数
增加条数
总条 数
仔细观察表格,你能发现哪些信息 有什么规律?
2
1
3
2
3
4
3
6
5
4
10
6
5
15
……
……
……
探究新知
1、点数-1=增加条数
2、总条数=1+2+3+……
增加条数=点数-1
3、总条数=点数×(增加条数)÷2
适用3个点以上情形
总条数=点数×(点数-1)÷2
图形 点数
增加条数
总条 数
仔细观察表格,你能发现哪些信息 有什么规律?
2
1
3
2
3
4
3
6
5
4
10
6
5
15
……
……
……
探究新知
当3个点时,总条数是1+2,即2个连续自然数相加。
当4个点时,总条数是1+2+3,即3个连续自然数相加。
当n个点时,总条数是1+2+3+……,即n-1个连续自然数相加。
A
E
D
C
B
已连接
已连接
已连接
已连接
已连接
已连接
全部已连接
探究新知
当5个点时,上述线条的个数就是4+3+2+1
4个连续自然数的和
所以,点数与线段之间的关系为:
n—1个连续自然数的和。
探究新知
1、同学们还记得连续自然数相加的求和公式吗?
1+2+3+4+……+n=n×(n+1)÷2
2、通过上面三种方法的观察,当有n个点时,它的总条 数是n-1个连续自然数的和,那么我们能不能根据点数来求出线段总条数呢?
把上面的n换成n-1试试看。
n×(n+1)÷2
(n-1)×[(n-1)+1)]÷2
(n-1)×n÷2
n× (n-1) ÷2
探究新知
我们也可以这样来理解:
n-1个连续自然数的和,可以先算n个连续自然数的和,然后再减n本身。
n×(n+1)÷2-n
=n×[(n+1)÷2-1]
=n× (+)
=n× ( - )
=n× (n-1)÷2
探究新知
连接7个点,会连成多少条线段?12个点,25个点呢?
总条数=点数×(点数-1)÷2
总条数=7×(7-1)÷2=21
总条数=12×(12-1)÷2=66
总条数=25×(25-1)÷2=300
同学们,在我们生活中有许多看似复杂的问题,我们都可以尝试从简单问题去思考,逐步找到其中的规律,从而来解决复杂的问题。
遇到复杂的问题的处理方法
3. 有序思考
2. 画图、枚举
1. 化繁为简
4. 探究规律
探究新知
基础练习
一、填空
1、6个点可以连成线段的条数是( )。
2、1,3,2,6,4,( ),( ),12,( )。
3、按规律填数:3、15、35、63、99、( )、195。
4、 一个长方形被剪去一个角后,还剩( )个角或( )个角,或( )个角。
15
9
8
16
奇数位上的数后一个是前一个的2倍
偶数位上的数后一个比前一个多3
143
连续奇数的积。
5
4
3
2、想一想,算一算:
寒假过去了,10个好朋友见面了,每两位好朋友握手一次,请同学们帮忙算算,他们一共握了多少次手?
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45(次)
答:一共握了45次手。
10 × (10 - 1) ÷ 2 = 45 (次)
( 1 + 9 ) × 9 ÷ 2 = 45 (次)
基础练习
n×(n+1)÷2(连续自然数求和公式)
n×(n-1)÷2
拓展练习
1、某小学开展秋季球类运动会,学校一共有8个篮球运动队,比赛采取对对见面的方式,你能不能算一下,第一轮比赛需要打几场球赛?
8×(8-1)÷2=28(场)
7+6+5+4+3+2+1=7×(7+1)÷2=28(场)
答:第一轮比赛需要打28场比赛。
拓展练习
2、用3,4,5,6四张数字卡片,每次取两张组成一个两位数,可以组成多少个偶数?
十位
个位
可填4个数
每个十位数据后可填3个数
4
×
3
=12
一共可以组成12个数。
十位
个位
可填2个数
每个个位数字前面可填3个数
3
×
2
=6
一共可以组成6个偶数。
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
