六年级下册数学 人教版 4.2.1 正比例 (教材P43页例1)课件(共23张PPT)
文档属性
| 名称 | 六年级下册数学 人教版 4.2.1 正比例 (教材P43页例1)课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-12 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
1.正比例
(教材P43例1)
人教版数学六年级下册
第四单元 正比例和反比例
复习旧知
1、路程、速度与时间。
一、说一说下面量之间的关系,并用等式表示出来。
2、总价、数量和单价。
3、工作总量、工作时间和工作效率。
路程=速度×时间;
时间=路程÷速度;
速度=路程÷时间。
总价=数量×单价;
数量=总价÷单价;
单价=总价÷数量。
工作总量=工作时间×工作效率;
工作效率=工作总量÷工作时间。
工作时间=工作总量÷效率;
复习旧知
二、计算
1、小华4小时走16km,按这样的速度,他10小时能走多少km
2、李大叔3小时加工零件90个,按这样的速度,他9小时能加工多少个零件?
3、爸爸用200元买了100棵树苗,按这样的价格,他要买4000棵树苗得用多少钱?
16÷4×10=40(km)
90÷3×9=270(个)
200÷100×4000=8000(元)
文具店有一种彩带,销售的数量与总价的关系如下表。
数量/米
总价/元
1
3.5
2
7
3
10.5
4
14
5
17.5
6
24.5
7
21
8
28
…
…
探究新知
观察上表,回答下面的问题。
(3)相应的总价与数量的比分别是多少?比值是多少?
数量/米
总价/元
探究新知
(1)表中有哪两种量?
(2)总价是怎么随着数量的变化而变化的?
1
2
3
4
5
6
7
8
…
…
由少变多
由少变多
3.5
7
10.5
14
17.5
24.5
21
28
3.5:1=3.5
7:2=3.5
10.5:3=3.5
14:4=3.5
17.5:5=3.5
21:6=3.5
24.5:7=3.5
28:8=3.5
数量/米
总价/元
1
2
3
4
5
6
7
8
…
…
探究新知
由少变多
由少变多
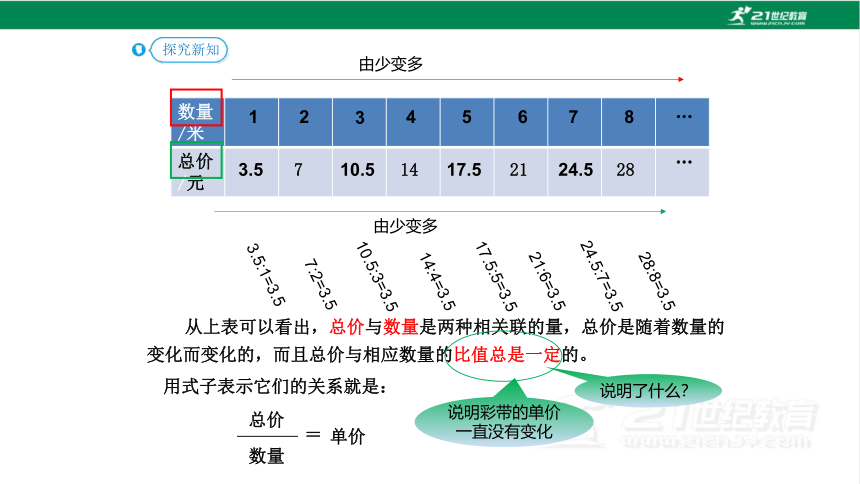
从上表可以看出,总价与数量是两种相关联的量,总价是随着数量的变化而变化的,而且总价与相应数量的比值总是一定的。
说明了什么?
说明彩带的单价一直没有变化
用式子表示它们的关系就是:
单价
总价
数量
=
3.5
7
10.5
14
17.5
24.5
21
28
3.5:1=3.5
7:2=3.5
10.5:3=3.5
14:4=3.5
17.5:5=3.5
21:6=3.5
24.5:7=3.5
28:8=3.5
数量/米
总价/元
1
2
3
4
5
6
7
8
…
…
探究新知
由少变多
由少变多
单价
总价
数量
=
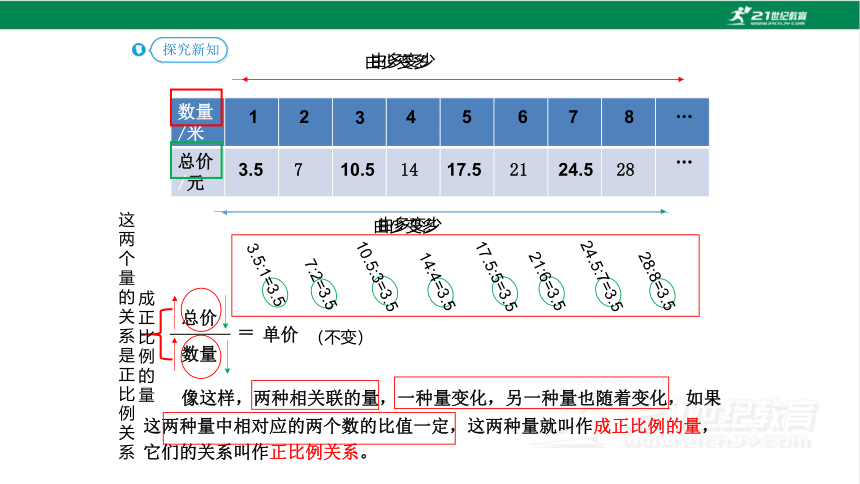
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
3.5
7
10.5
14
17.5
24.5
21
28
3.5:1=3.5
7:2=3.5
10.5:3=3.5
14:4=3.5
17.5:5=3.5
21:6=3.5
24.5:7=3.5
28:8=3.5
数量/米
总价/元
1
2
3
4
5
6
7
8
…
…
探究新知
由多变少
由少变多
单价
总价
数量
=
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
由少变多
由多变少
(不变)
成正比例的量
这两个量的关系是正比例关系
3.5
7
10.5
14
17.5
24.5
21
28
3.5:1=3.5
7:2=3.5
10.5:3=3.5
14:4=3.5
17.5:5=3.5
21:6=3.5
24.5:7=3.5
28:8=3.5
探究新知
请你说一说成正比例关系的三要素:
第一:必须有两种量,而且必须是相关联的量。
第二:一种量变化,另一种量也随着变化。
所谓的相关联,就是两个量之间有必然联系,比如一个人走路的时间与所走的路程,走的时间长,肯定走的路就多,时间短,肯定路就短;再比如一个工人加工零件的时间和数量,加工时间长,数量就多,时间短,数量就少;再比如,儿童年龄与个子,个子会随着年龄的增长而长大;这些量都是有关联的。但像你的个子与走路的时间,买东西所付的钱与你的年龄……这些量之间没有必然的联系,所以是不关联的量。
像上面一个人走路的时间与所走的路程,走的时间变化了,走的路肯定也随着变化;工人加工零件的时间和数量,加工时间变化了,数量也会变化 ;儿童的年龄与个子,年龄增长了,个子也会长大一些。
第三:两个量的比值一定。
走路的人如果速度不变,那么他走路的时间与所走的路程,就成正比例关系,如果时快时慢,时间与路程就不成正比例关系;工人加工零件的效率如果不变,那么他加工零件的时间和数量就成正比例关系,如果效率有变化,那么就不成正比例关系;儿童的年龄与个子虽然是相关联的两个量,个子与年龄的比值却不是一个定值,比如你一岁时身高30cm,2岁时身高必须是60cm,3岁时身高必须是90cm, ……10岁时身高必须是300cm,只有这样,两个量长成正比例关系,但显然是不会的。
三要素缺少其中的任意一个,都不成正比例关系。
上表中,总价和数量是成正比例的量,总价与数量成正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
总价
=
单价
数量
x
y
= k
数量/米
总价/元
1
3.5
2
7
3
10.5
4
14
5
17.5
6
24.5
7
21
8
28
…
…
探究新知
数量/米
总价/元
1
3.5
2
7
3
10.5
4
14
5
17.5
6
24.5
7
21
8
28
…
…
文具店有一种彩带,销售的数量与总价的关系如下表。
上面表格中的数据还可以用图象表示。
探究新知
(1)从图中你发现了什么?
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象
连起来并延长,你还能发现什么?
根据图象回答下面的问题:
探究新知
不同数量彩带的售价连起来是一条线段。
探究新知
发现:这些点会形成一条直线,随着数量的无限增加而延伸。
我们把这种表示 正比例关系的图象叫作正比例图象。正比例图象是一条直线。
基础练习
时间/小时 1 2 3 4 5
路程/km 80 160 240 320 400
甲汽车行驶的时间与路程统计表
1、下面是两个汽车行驶时间与路程的统计表,请你判断两辆汽车的行驶时间与路程是不是成正比例关系,并说说你的方法和理由。
时间/小时 1 2 3 4 5
路程/km 60 120 150 280 300
乙汽车行驶的时间与路程统计表
甲汽车每次路程与时间的比是:
80:1=80
160:2=80
240:3=80
320:4=80
400:5=80
路程与时间的比值始终是80,没有变化 ,所以甲汽车的路程与时间成正比例关系。
乙汽车每次路程与时间的比是:
60:1=60
120:2=60
150:3=50
280:4=70
300:5=60
路程与时间的比值有变化 ,并不是一个定值,所以乙汽车的路程与时间不成正比例关系。
基础练习
时间/小时 1 2 3 4 5
路程/km 80 160 240 320 400
甲汽车行驶的时间与路程统计表
2、把甲汽车行驶时间与路程用图象表示出来,并回答下面问题。
时间/小时
路程/km
0
40
80
120
160
200
240
280
320
360
400
1
2
3
4
5
基础练习
时间/小时
路程/km
0
40
80
120
160
200
240
280
320
360
400
1
2
3
4
5
(1)不计算,说一下甲汽车行驶到120km时,大约用了多长时间?
从图上可以看出,大约用了1.5小时。
(2)不计算,说一下甲汽车行驶到3.5小时时,大约行驶了多少km
从图上可以看出,大约行驶了280km。
拓展练习
二、判断下面每题中的两个量是否成正比例关系,并说明理由。
1、苹果的单价一定,购买苹果的数量与总价。
2、每袋面粉的质量一定,面粉总质量与总袋数。
3、小新跳高的高度与他的身高。
总价÷数量=单价,单价一定,说明总价与数量 的比值一定,所以这两个量成正比例关系
总质量÷袋数=每袋质量,每袋质量不变,说明总质量与总袋数的比值一定,所以这两个量成正比例关系
所跳高度与身高的比值不一定,所以这两个量不正比例关系。
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
拓展练习
……
数学阅读
这一天,数学王国来了一对奇妙的正反比例兄弟。大家感到十分惊奇,都凑过来想看个究竟,场面顿时一片混乱。这时,数学王国的国王走过来,对 大家说:“大家不要惊慌,这是我们数学家族的一员。只不过几十年前,他们的祖先因为某些 原因和我们失散了。现在,他们又回来了。下面,就请他们介绍一下自己吧! ”听了国王的 话,大家恍然大悟,原来是一家人啊!
正比例首先向大家介绍了自己:“大家好!我叫正比例,就如国王刚才说的那样,在几十 年前我们也是一家人。但是,我们和你们又有些不同的地方,因为大家都表示一个数或一种关 系,而我和我的弟弟则是表示两种相关联的量的关系。我这么说,大 家一定还没听懂,我给大家举个例子吧!大家用完全相同的圆柱杯子去接水,你所接的水的体积和水的高度就是两个成正比例的量,假如接1厘米高时水的体积是10立方厘米,那么接2厘米高就是20立方厘米,接8厘米高就是80立方厘米……。两种相关联的量,一种量变化,另一种量也随着变化,如果这两 种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系 叫做成正比例关系。像刚才接水的例子,高如果增加,体积也随之增加,所以,它的体积和高成正比例。说得再简单一点,就是如果一样事物增加了,另一样事物也随之增加,它减少了, 另一样事物也随之减少,这两个事物的关系就叫做成正比例关系。生活中还有许多这样的例 子,如:当某物品的单价一定时,它的总价和数量成正比例;当速度一定时,路程和时间成正比例;当工作效率一定时,工作总量和工作时间成正比例等等。我就是专门用来表示上面这种关系的。 ”
听完正比例的介绍,大家总算明白了正比例是什么。(未完待续……)
正反比例的故事(一)
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.正比例
(教材P43例1)
人教版数学六年级下册
第四单元 正比例和反比例
复习旧知
1、路程、速度与时间。
一、说一说下面量之间的关系,并用等式表示出来。
2、总价、数量和单价。
3、工作总量、工作时间和工作效率。
路程=速度×时间;
时间=路程÷速度;
速度=路程÷时间。
总价=数量×单价;
数量=总价÷单价;
单价=总价÷数量。
工作总量=工作时间×工作效率;
工作效率=工作总量÷工作时间。
工作时间=工作总量÷效率;
复习旧知
二、计算
1、小华4小时走16km,按这样的速度,他10小时能走多少km
2、李大叔3小时加工零件90个,按这样的速度,他9小时能加工多少个零件?
3、爸爸用200元买了100棵树苗,按这样的价格,他要买4000棵树苗得用多少钱?
16÷4×10=40(km)
90÷3×9=270(个)
200÷100×4000=8000(元)
文具店有一种彩带,销售的数量与总价的关系如下表。
数量/米
总价/元
1
3.5
2
7
3
10.5
4
14
5
17.5
6
24.5
7
21
8
28
…
…
探究新知
观察上表,回答下面的问题。
(3)相应的总价与数量的比分别是多少?比值是多少?
数量/米
总价/元
探究新知
(1)表中有哪两种量?
(2)总价是怎么随着数量的变化而变化的?
1
2
3
4
5
6
7
8
…
…
由少变多
由少变多
3.5
7
10.5
14
17.5
24.5
21
28
3.5:1=3.5
7:2=3.5
10.5:3=3.5
14:4=3.5
17.5:5=3.5
21:6=3.5
24.5:7=3.5
28:8=3.5
数量/米
总价/元
1
2
3
4
5
6
7
8
…
…
探究新知
由少变多
由少变多
从上表可以看出,总价与数量是两种相关联的量,总价是随着数量的变化而变化的,而且总价与相应数量的比值总是一定的。
说明了什么?
说明彩带的单价一直没有变化
用式子表示它们的关系就是:
单价
总价
数量
=
3.5
7
10.5
14
17.5
24.5
21
28
3.5:1=3.5
7:2=3.5
10.5:3=3.5
14:4=3.5
17.5:5=3.5
21:6=3.5
24.5:7=3.5
28:8=3.5
数量/米
总价/元
1
2
3
4
5
6
7
8
…
…
探究新知
由少变多
由少变多
单价
总价
数量
=
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
3.5
7
10.5
14
17.5
24.5
21
28
3.5:1=3.5
7:2=3.5
10.5:3=3.5
14:4=3.5
17.5:5=3.5
21:6=3.5
24.5:7=3.5
28:8=3.5
数量/米
总价/元
1
2
3
4
5
6
7
8
…
…
探究新知
由多变少
由少变多
单价
总价
数量
=
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
由少变多
由多变少
(不变)
成正比例的量
这两个量的关系是正比例关系
3.5
7
10.5
14
17.5
24.5
21
28
3.5:1=3.5
7:2=3.5
10.5:3=3.5
14:4=3.5
17.5:5=3.5
21:6=3.5
24.5:7=3.5
28:8=3.5
探究新知
请你说一说成正比例关系的三要素:
第一:必须有两种量,而且必须是相关联的量。
第二:一种量变化,另一种量也随着变化。
所谓的相关联,就是两个量之间有必然联系,比如一个人走路的时间与所走的路程,走的时间长,肯定走的路就多,时间短,肯定路就短;再比如一个工人加工零件的时间和数量,加工时间长,数量就多,时间短,数量就少;再比如,儿童年龄与个子,个子会随着年龄的增长而长大;这些量都是有关联的。但像你的个子与走路的时间,买东西所付的钱与你的年龄……这些量之间没有必然的联系,所以是不关联的量。
像上面一个人走路的时间与所走的路程,走的时间变化了,走的路肯定也随着变化;工人加工零件的时间和数量,加工时间变化了,数量也会变化 ;儿童的年龄与个子,年龄增长了,个子也会长大一些。
第三:两个量的比值一定。
走路的人如果速度不变,那么他走路的时间与所走的路程,就成正比例关系,如果时快时慢,时间与路程就不成正比例关系;工人加工零件的效率如果不变,那么他加工零件的时间和数量就成正比例关系,如果效率有变化,那么就不成正比例关系;儿童的年龄与个子虽然是相关联的两个量,个子与年龄的比值却不是一个定值,比如你一岁时身高30cm,2岁时身高必须是60cm,3岁时身高必须是90cm, ……10岁时身高必须是300cm,只有这样,两个量长成正比例关系,但显然是不会的。
三要素缺少其中的任意一个,都不成正比例关系。
上表中,总价和数量是成正比例的量,总价与数量成正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
总价
=
单价
数量
x
y
= k
数量/米
总价/元
1
3.5
2
7
3
10.5
4
14
5
17.5
6
24.5
7
21
8
28
…
…
探究新知
数量/米
总价/元
1
3.5
2
7
3
10.5
4
14
5
17.5
6
24.5
7
21
8
28
…
…
文具店有一种彩带,销售的数量与总价的关系如下表。
上面表格中的数据还可以用图象表示。
探究新知
(1)从图中你发现了什么?
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象
连起来并延长,你还能发现什么?
根据图象回答下面的问题:
探究新知
不同数量彩带的售价连起来是一条线段。
探究新知
发现:这些点会形成一条直线,随着数量的无限增加而延伸。
我们把这种表示 正比例关系的图象叫作正比例图象。正比例图象是一条直线。
基础练习
时间/小时 1 2 3 4 5
路程/km 80 160 240 320 400
甲汽车行驶的时间与路程统计表
1、下面是两个汽车行驶时间与路程的统计表,请你判断两辆汽车的行驶时间与路程是不是成正比例关系,并说说你的方法和理由。
时间/小时 1 2 3 4 5
路程/km 60 120 150 280 300
乙汽车行驶的时间与路程统计表
甲汽车每次路程与时间的比是:
80:1=80
160:2=80
240:3=80
320:4=80
400:5=80
路程与时间的比值始终是80,没有变化 ,所以甲汽车的路程与时间成正比例关系。
乙汽车每次路程与时间的比是:
60:1=60
120:2=60
150:3=50
280:4=70
300:5=60
路程与时间的比值有变化 ,并不是一个定值,所以乙汽车的路程与时间不成正比例关系。
基础练习
时间/小时 1 2 3 4 5
路程/km 80 160 240 320 400
甲汽车行驶的时间与路程统计表
2、把甲汽车行驶时间与路程用图象表示出来,并回答下面问题。
时间/小时
路程/km
0
40
80
120
160
200
240
280
320
360
400
1
2
3
4
5
基础练习
时间/小时
路程/km
0
40
80
120
160
200
240
280
320
360
400
1
2
3
4
5
(1)不计算,说一下甲汽车行驶到120km时,大约用了多长时间?
从图上可以看出,大约用了1.5小时。
(2)不计算,说一下甲汽车行驶到3.5小时时,大约行驶了多少km
从图上可以看出,大约行驶了280km。
拓展练习
二、判断下面每题中的两个量是否成正比例关系,并说明理由。
1、苹果的单价一定,购买苹果的数量与总价。
2、每袋面粉的质量一定,面粉总质量与总袋数。
3、小新跳高的高度与他的身高。
总价÷数量=单价,单价一定,说明总价与数量 的比值一定,所以这两个量成正比例关系
总质量÷袋数=每袋质量,每袋质量不变,说明总质量与总袋数的比值一定,所以这两个量成正比例关系
所跳高度与身高的比值不一定,所以这两个量不正比例关系。
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
拓展练习
……
数学阅读
这一天,数学王国来了一对奇妙的正反比例兄弟。大家感到十分惊奇,都凑过来想看个究竟,场面顿时一片混乱。这时,数学王国的国王走过来,对 大家说:“大家不要惊慌,这是我们数学家族的一员。只不过几十年前,他们的祖先因为某些 原因和我们失散了。现在,他们又回来了。下面,就请他们介绍一下自己吧! ”听了国王的 话,大家恍然大悟,原来是一家人啊!
正比例首先向大家介绍了自己:“大家好!我叫正比例,就如国王刚才说的那样,在几十 年前我们也是一家人。但是,我们和你们又有些不同的地方,因为大家都表示一个数或一种关 系,而我和我的弟弟则是表示两种相关联的量的关系。我这么说,大 家一定还没听懂,我给大家举个例子吧!大家用完全相同的圆柱杯子去接水,你所接的水的体积和水的高度就是两个成正比例的量,假如接1厘米高时水的体积是10立方厘米,那么接2厘米高就是20立方厘米,接8厘米高就是80立方厘米……。两种相关联的量,一种量变化,另一种量也随着变化,如果这两 种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系 叫做成正比例关系。像刚才接水的例子,高如果增加,体积也随之增加,所以,它的体积和高成正比例。说得再简单一点,就是如果一样事物增加了,另一样事物也随之增加,它减少了, 另一样事物也随之减少,这两个事物的关系就叫做成正比例关系。生活中还有许多这样的例 子,如:当某物品的单价一定时,它的总价和数量成正比例;当速度一定时,路程和时间成正比例;当工作效率一定时,工作总量和工作时间成正比例等等。我就是专门用来表示上面这种关系的。 ”
听完正比例的介绍,大家总算明白了正比例是什么。(未完待续……)
正反比例的故事(一)
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
