人教版(2023春)数学五年级下册综合与实践 探索图形课件(共22张PPT)
文档属性
| 名称 | 人教版(2023春)数学五年级下册综合与实践 探索图形课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
人教版数学五年级下册
第三单元 长方体和正方体
探索图形
(教材P44)
情境导入
用棱长为1 cm的小正方体拼成如下的大正方体,说一说每个大正方体分别是由多少块小正方体组成的?
探究新知
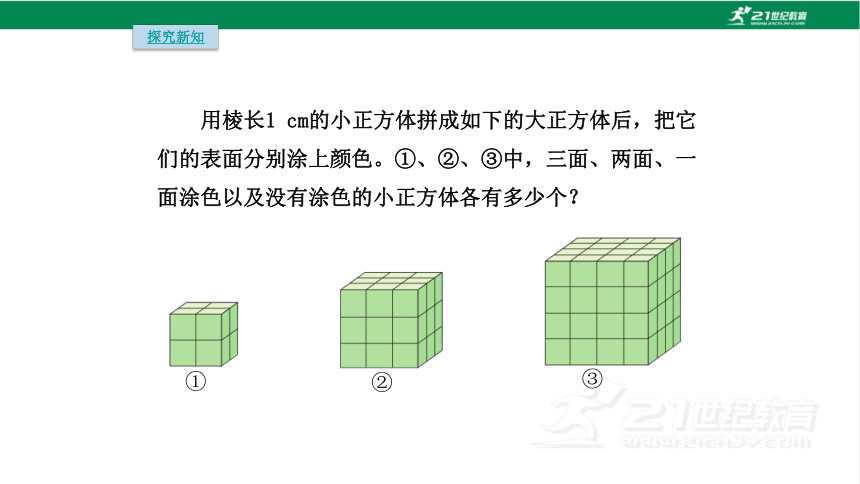
用棱长1 cm的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。①、②、③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少个?
①
②
③
探究新知
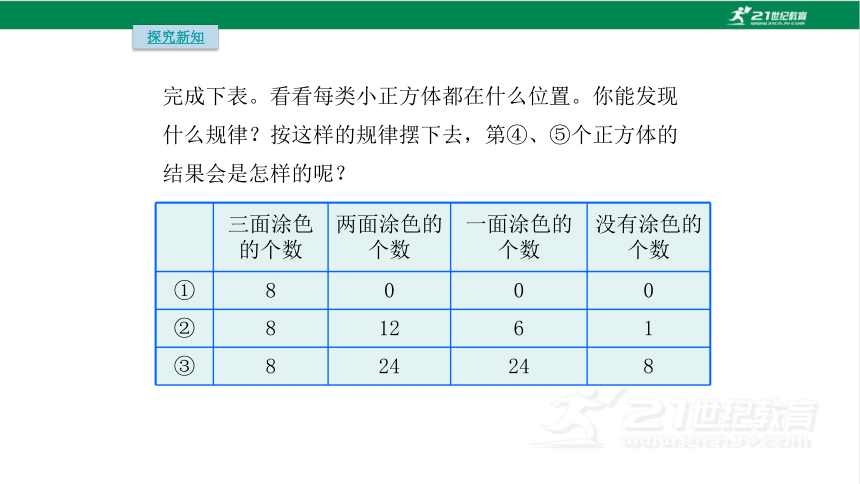
三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
完成下表。看看每类小正方体都在什么位置。你能发现什么规律?按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
探究新知
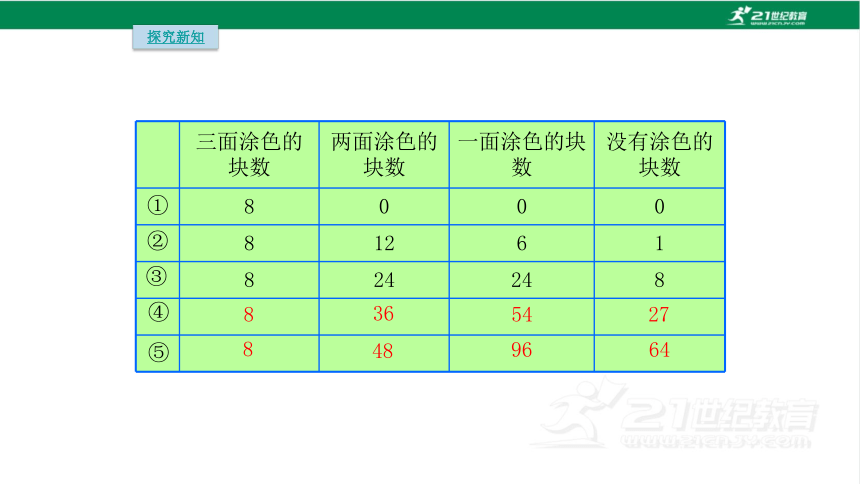
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
8 0 0 0
8 12 6 1
8 24 24 8
8
36
54
27
8
48
96
64
①
②
③
④
⑤
探究新知
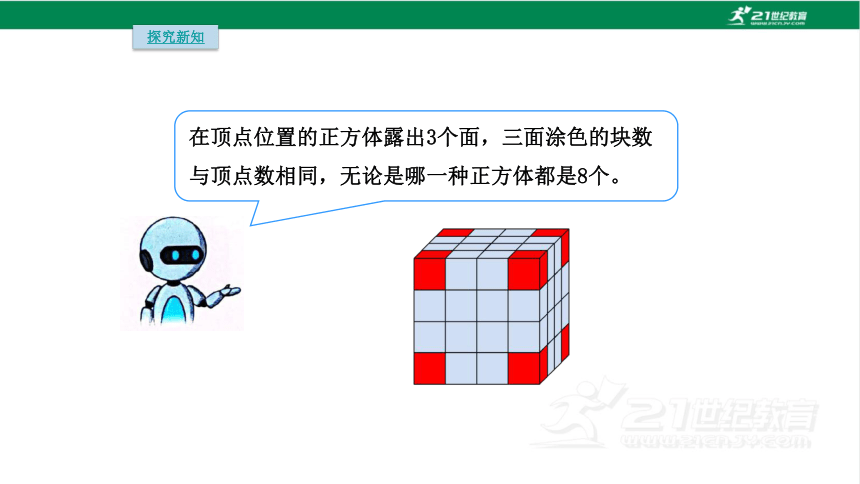
在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
探究新知
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
探究新知
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。
探究新知
将涂过色的小正方体进行剥离。
探究新知
探究新知
没涂色的块数是(n-2)×(n-2)×(n-2)。
探究新知
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
(1) 你能继续写出第⑥、⑦、⑧个大正方体中4类小正方体的块数吗?
8
60
150
125
8
72
216
216
8
84
294
343
⑥
⑦
⑧
探究新知
(2)如果摆成下面的几何体,你会数吗?
4
10
20
1.判断。
(1)长方体是特殊的正方体。( )
(2)正方体的棱长扩大到原来的3倍,体积就扩大到原来的9倍。( )
(3)把两个一样的正方体拼成一个长方体后,体积和表面积都不变。( )
(4)一瓶白酒有500 L。( )
×
×
×
×
基础练习
2.精挑细选。
(1)一种水箱最多可以装水80 L,我们就说这种水箱的( )是80 L。
A.底面积 B.表面积 C.容积 D.质量
(2)把两个棱长都是10 cm的正方体拼成一个长方体后,表面积减少( ) cm2 。
A.100 B.200 C.80 D.1000
(3)一根长方体钢材的横截面积是110 cm2 ,长是0.5 m,它的体积是( ) cm3 。
A.55 B.5500 C.550 D.55000
(4)一个正方体的棱长是a m,如果它的高增加3 m变成一个长方体,那么它的体积比原正方体增加( ) m3 。
A.9×a B.6×a×a C.3×a×a D.3×a
C
B
B
C
基础练习
有一个长方体(如图),它的底面和右面的面积之和是125平方厘米,且长、宽、高都是质数。那么,这个长方体的体积是多少立方厘米?
依据“底面和右面的面积之和是125平方厘米”,可得下面的关系式:a×b+b×h=125,即 b×(a+h)=125;
a、b、h为质数,b为质数,b为质数时,125只有分解成5×25,则b×(a+h)=5×25;
a+h=25,那么a+h又是哪两个质数相加的和呢?即可推出25=23+2符合条件。
因此,长方体的长、宽、高分别是23、5、2,所求体积是:23×5×2=230(立方厘米)
拓展练习
你学到了
什么?
课堂小结
立方体,也称正方体,是由6个正方形面组成的正多面体,故又称正六面体。它有12条边和8个顶点。正方体是特殊的长方体。
日常生活中,食盐和糖的结晶体都是立方状。骰子最常见的形状就是立方体。
立方体的横切面共有四种:三角形、四边形、五边形、六边形、其中以正六边形的面积最大。
立方体
数学阅读
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版数学五年级下册
第三单元 长方体和正方体
探索图形
(教材P44)
情境导入
用棱长为1 cm的小正方体拼成如下的大正方体,说一说每个大正方体分别是由多少块小正方体组成的?
探究新知
用棱长1 cm的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。①、②、③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少个?
①
②
③
探究新知
三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
完成下表。看看每类小正方体都在什么位置。你能发现什么规律?按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
探究新知
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
8 0 0 0
8 12 6 1
8 24 24 8
8
36
54
27
8
48
96
64
①
②
③
④
⑤
探究新知
在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
探究新知
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
探究新知
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。
探究新知
将涂过色的小正方体进行剥离。
探究新知
探究新知
没涂色的块数是(n-2)×(n-2)×(n-2)。
探究新知
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
(1) 你能继续写出第⑥、⑦、⑧个大正方体中4类小正方体的块数吗?
8
60
150
125
8
72
216
216
8
84
294
343
⑥
⑦
⑧
探究新知
(2)如果摆成下面的几何体,你会数吗?
4
10
20
1.判断。
(1)长方体是特殊的正方体。( )
(2)正方体的棱长扩大到原来的3倍,体积就扩大到原来的9倍。( )
(3)把两个一样的正方体拼成一个长方体后,体积和表面积都不变。( )
(4)一瓶白酒有500 L。( )
×
×
×
×
基础练习
2.精挑细选。
(1)一种水箱最多可以装水80 L,我们就说这种水箱的( )是80 L。
A.底面积 B.表面积 C.容积 D.质量
(2)把两个棱长都是10 cm的正方体拼成一个长方体后,表面积减少( ) cm2 。
A.100 B.200 C.80 D.1000
(3)一根长方体钢材的横截面积是110 cm2 ,长是0.5 m,它的体积是( ) cm3 。
A.55 B.5500 C.550 D.55000
(4)一个正方体的棱长是a m,如果它的高增加3 m变成一个长方体,那么它的体积比原正方体增加( ) m3 。
A.9×a B.6×a×a C.3×a×a D.3×a
C
B
B
C
基础练习
有一个长方体(如图),它的底面和右面的面积之和是125平方厘米,且长、宽、高都是质数。那么,这个长方体的体积是多少立方厘米?
依据“底面和右面的面积之和是125平方厘米”,可得下面的关系式:a×b+b×h=125,即 b×(a+h)=125;
a、b、h为质数,b为质数,b为质数时,125只有分解成5×25,则b×(a+h)=5×25;
a+h=25,那么a+h又是哪两个质数相加的和呢?即可推出25=23+2符合条件。
因此,长方体的长、宽、高分别是23、5、2,所求体积是:23×5×2=230(立方厘米)
拓展练习
你学到了
什么?
课堂小结
立方体,也称正方体,是由6个正方形面组成的正多面体,故又称正六面体。它有12条边和8个顶点。正方体是特殊的长方体。
日常生活中,食盐和糖的结晶体都是立方状。骰子最常见的形状就是立方体。
立方体的横切面共有四种:三角形、四边形、五边形、六边形、其中以正六边形的面积最大。
立方体
数学阅读
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
